扁平型永磁直线电机定位力综合优化

史石磊，康尔良,史桂英

(1.哈尔滨理工大学 电气与电子工程学院，哈尔滨150080；2.黑龙江省高校直驱传动系统工程技术创新中心，哈尔滨 150080；3.哈尔滨泰富电机有限公司，哈尔滨 150080)

0 引 言

伴随着数控加工产业的换代升级，对数控机床提出了高精度、高速度和高稳定性的要求。相比于旋转电机的传动系统，永磁直线电机传动系统具有功率密度大、响应速度快、精度高等特点，这使其在高精度机床进给系统中得到了广泛的应用，从而推动了永磁直线电机相关研究的发展。

由于永磁直线电机存在端部效应和齿槽效应，这使得永磁直线电机存在很大的定位力波动，直接影响了其控制精度。针对定位力的削弱，学者们进行了相关研究。文献[1]提出了多种抑制定位力波动的方法并指出在电机设计阶段应进行多目标的优化设计；文献[2]通过对永磁直线电机左、右两侧的端部力进行频谱分析的基础上，采用最佳铁芯长度和端部增加阶梯型辅助铁轭的方法来削弱端部力。文献[3]采用等效磁化强度法得到了无铁芯永磁直线电机的推力波动的解析表达式，引入重心邻域法进行了多目标优化设计。并通过实验验证了方法的有效性。文献[4]采用遗传算法对一台圆筒永磁直线电机的齿槽力进行了综合优化设计。文献[5]基于子域模型解析了永磁直线电机的电磁力并提出了增加辅助齿的方法来削弱端部力。文献[6]结合解析法与磁路法对永磁直线电机的参数进行了解析，并通过二维有限元软件仿真验证了方法的合理性。文献[7]以同步发电机效率为目标，采用田口法对电机进行了优化设计，并通过有限元仿真验证了优化结果。

本文以一台18槽21极的扁平型永磁直线电机为优化对象，首先对定位力的产生原因进行了解析，得到了影响定位力的关键参数。然后选取边齿宽度、斜极长度、磁钢宽度和磁钢厚度作为优化变量，以定位力峰-峰值、反电势幅值和单块磁钢用量为优化目标，结合有限元法和田口法进行优化设计，得到优化变量的最优组合，通过有限元对比了初始方案和优化方案的性能指标。最后通过测试样机的定位力和反电势验证了方法的有效性。

1 永磁直线电机定位力解析

永磁直线电机可视为把传统的永磁旋转电机从圆周上某点沿轴向断开后再将原来的圆周面拉伸为平面。如图1中所示，由于铁心的开断使得电机出现了两个端部，在N、S极交替分布的磁钢上运动必然产生推力波动，这种推力的波动称之为端部力，此外由于铁心开槽引起的齿槽效应也会产生推力波动，这种推力波动称之为齿槽力。端部力Fend和齿槽力Fsolt叠加在一起构成了永磁直线电机的定位力Fdent即：

Fdent=Fend+Fslot

(1)

图1 永磁旋转电机与永磁直线结构对比图

文献[8]通过对端部磁通变化规律的基础上，通过虚位移法得到了端部推力波动的表达式。对于极数为2p的铁心纵向长度Ls=2p+λ端部力Fend为

(2)

式中，Kc为卡式系数；δ为气隙长度；Φm为穿过端部的最大磁通幅值；μ0为真空磁导率；k1为磁通压缩系数；为极距；lef为铁心有效叠厚。

由式(1)可知当λ=0时，端部力幅值增加两倍；当λ=/2时，奇数谐波被削去，只剩下偶次分量，端部力幅值为2KcδΦm2/μ0k12lef。通过对铁心纵向长度的合理调整可以削弱端部力。

文献[9]采用虚位移法对旋转永磁电机的齿槽转矩进行了解析计算。由于结构上可以将永磁直线电机看作是旋转永磁电机的演变，因此可以采用旋转永磁电机分析齿槽转矩的方法来分析永磁直线电机的齿槽力。不考虑端部力的影响，永磁直线电机沿直线方向的位移相当于旋转电机中转过的角度：

(3)

磁场能量W为

(4)

(5)

式中，Br为磁钢剩磁，δ(θ,α)为气隙有效长度，hm为磁钢厚度。则永磁直线电机的齿槽力为

(6)

式中，z为铁心槽数，Bnz/2p为剩磁的nz/2p次谐波。由齿槽力的表达式可知极弧系数和磁钢厚度等变量直接影响永磁直线电机的齿槽力。

2 永磁直线电机初始方案

根据经典的旋转永磁电机设计的计算公式推导出适合永磁直线电机的电磁计算公式，确定了永磁直线电机的初始方案，电机的具体结构参数如图1所示。

表1 初始方案电机参数

根据电机初始方案的结构参数建立二维有限元仿真模型[10]，如图2所示。为了考虑分析端部力和齿槽槽力对定位力的影响，分别建立了仅考虑端部力作用和仅靠考虑铁心开槽作用时的电机模型，如图3、图4所示。

图2 扁平永磁直线电机仿真模型

图3 端部力仿真模型

图4 齿槽仿真模型

根据上述3种模型对电机定位力进行仿真，仿真中暂不考虑斜槽作用，结果如图5所示，从图中可以看出定位力可由端部力和齿槽力的叠加得到，其中，齿槽力和端部力的波动周期为2倍的电周期，并且二者相位相差半个周期，这使得叠加后的定位力小于端部力。因此可知，齿槽力和端部力可以通过合理的结构设计进行相互削弱，从而使得定位力波动减小。

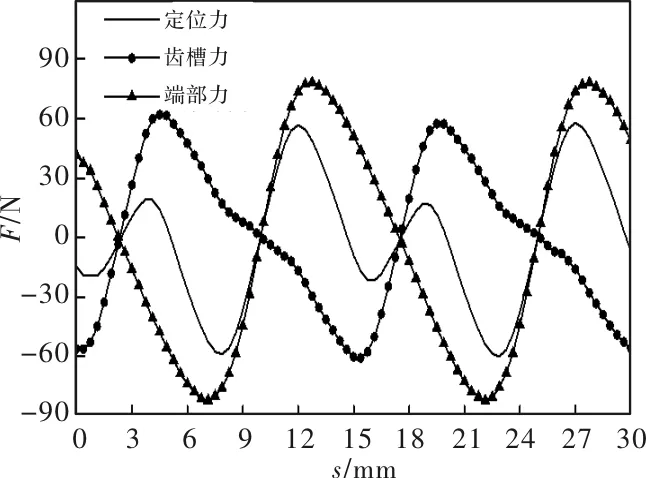
图5 齿槽仿真模型

3 田口法优化设计

目前常用于电机优化设计的算法有遗传算法、粒子群算法、模拟退火法等，但这些算法需要通过繁杂的数学推导建立目标函数和约束条件。相比于这些算法，田口法操作起来更加高效、方便，只需根据控制变量和优化目标建立代表实验组合的交直表就能完成目标优化。由于田口法优化的高效性和有效性使其在工程实践中得到广泛应用。

基于有限元和田口法优化设计步骤：①确定优化目标和优化变量，并选取各变量水准值。②根据优化参数水准值建立交直实验表，并通过有限元进行仿真实验的到各组实验数据。③通过对分析实验数据，确定最佳的优化参数组合。利用有限元对最优变量组合进行仿真验证。

3.1 优化目标及变量选取

定位力和反电势是永磁直线电机重要性能指标，定位力影响永磁直线电机伺服系统的定位精度，反电势直接关系到电机的带载能力。此外，如图1所示，对于短初级-长次级结构形式直线电机来说，初级运动形成受到次级磁钢沿运动方向排列长度的限制，行程越长需要布置的磁钢就越多，而磁钢的用量直接影响着永磁直线电机的制造成本。因此，选择定位力峰-峰值F、反电势幅值E和单块磁钢M用量作为优化目标，以期在磁钢用量较小的情况下得到最佳的定位力峰-峰值和反电势幅值。

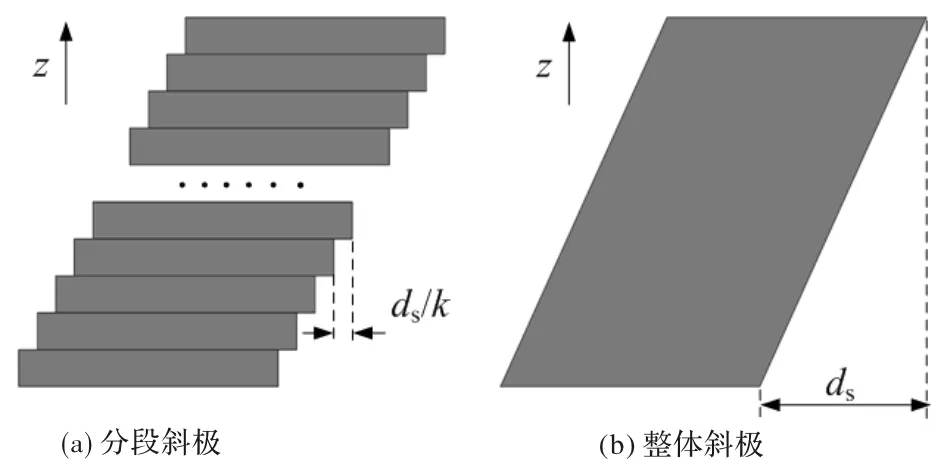
图6 斜极示意图

电机设计过程中，斜极或斜槽是常用来削弱齿槽转矩的有效方法，而直线电机很难实现铁芯斜齿的结构，所以通常采用斜极来削弱定位力。定义斜极长度ds为斜极后磁钢对角点在运动方向上的位移差，如图6(b)所示。由于采用二维有限元模型进行仿真，所以斜极需要通过分段斜极进行等效计算，如图6(a)所示，本文采用23段分段斜极进行等效。

表2 控制变量的水准值

根据对定位力的解析，可知初级长度Ls、极弧系数α和磁钢厚度hm对定位力波动有着直接影响，在本文中决定初级长度的变量为边齿宽度bet，而决定极弧系数的变量为磁钢宽度bm。因此选取边齿宽度bet、斜极长度ds、磁钢宽度bm和磁钢厚度hm为优化变量，分别取4个变量的5个水准值，如表2所示。

3.2 建立交直实验表进行仿真实验

根据常规的实验方法，4个变量，5中水准值需要进行45组仿真实验，而根据田口法选则L25(54)交直表进行实验，只需进行25组仿真实验。根据选取的优化变量和优化目标建立交直实验表及仿真实验结果如表3所示。

表3 交直实验表与仿真结果

3.3 仿真结果分析

按式(7)分别求出每个变量在各个水准下的平均值，计算结果如表4所示。

(7)

为了得到各优化变量对优化目标的影响比重，需进一步求取方差进行分析。计算公式如下：

(8)

(9)

式中：Gi为优化目标在第i次仿真实验的值。

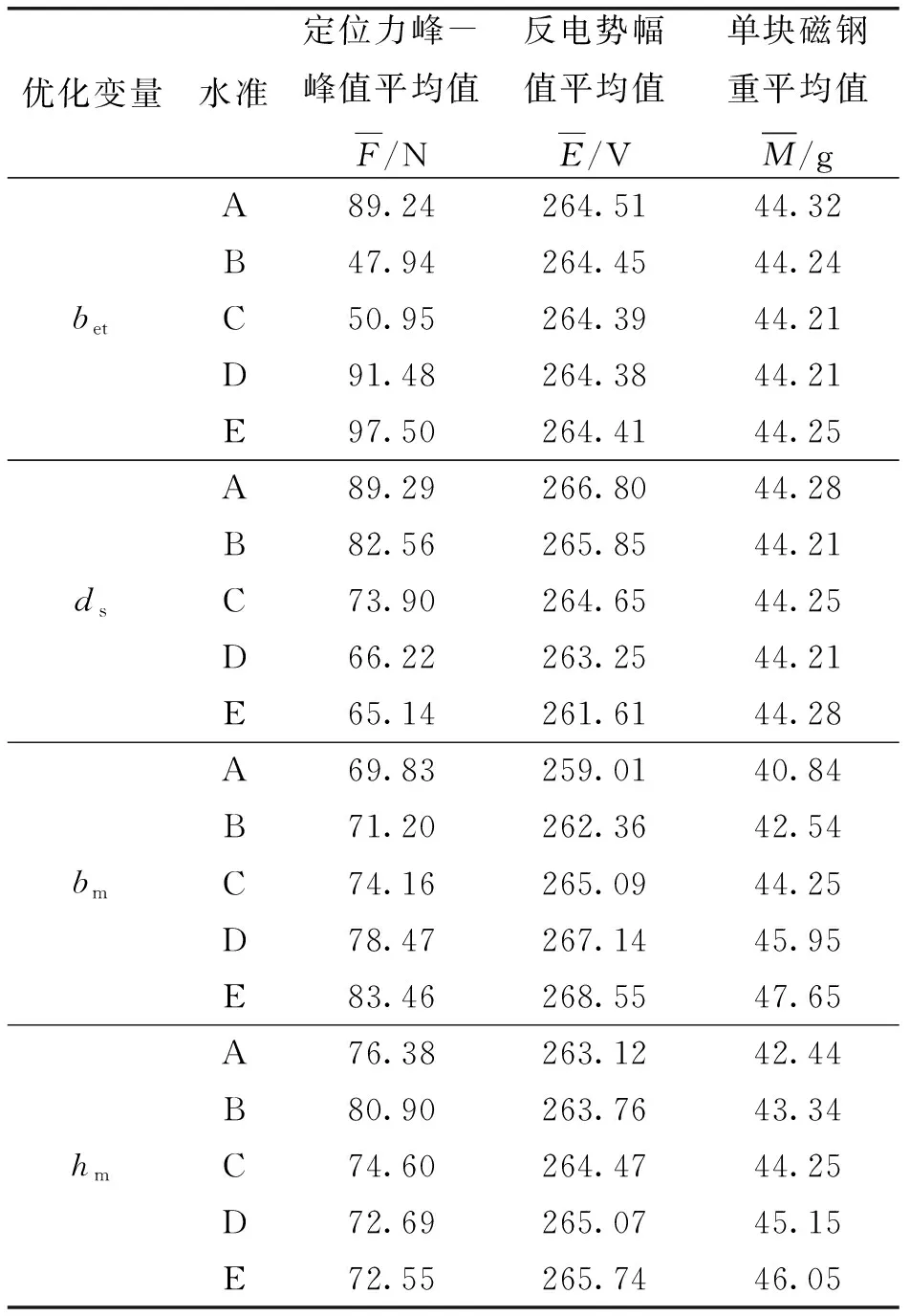
表4 各优化目标平均值

表5 各优化变量对目标影响比重

从表5中可以看出，边齿宽度对定位力影响比重最大；斜极长度对定位力和反电势的影响比重都排在第二位，但是斜极长度对反电势影响略大于对定位力的影响；磁钢宽度对反电势和磁钢用量的影响比重最大，但磁钢宽度对磁钢用量的影响略大于对反电势的影响；磁钢厚度主要对磁钢用量影响较大，而对定位力和反电势的作用不大。当以定位力最小为优化目标，则边齿宽度应选择水准B。考虑在削弱定位力的同时尽量减小反电势的损失，斜极长度选择水准D。同样考虑磁钢用量最小时尽可能的增加反电势，磁钢宽度也选择水准D。以磁钢用量最小为优化目标，则磁钢宽度选者水准A。最终得到优化水准组合为B、D、D、A。

表6 参数对比

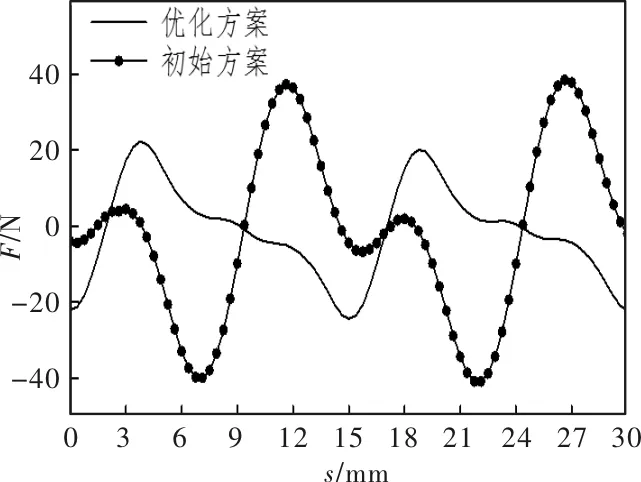
图7 定位力波形对比

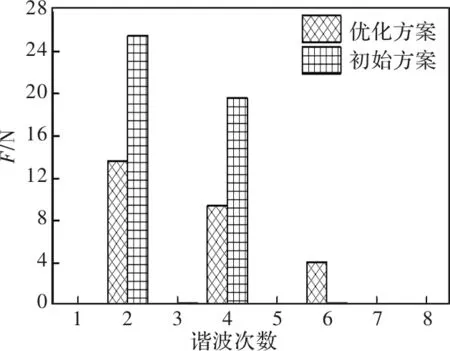
图8 定位力频谱分析对比

根据优化后的尺寸进行有限元仿真计算。初始方案与优化方案的参数如表6所示，定位力波形对比如图7所示。经过优化设计后，定位力峰-峰值减小了41.1%，反电势增加了0.86%，单块磁钢减重4.3%。实现了优化目标。图8为初始方案与优化方案定位力的频谱分析对比，从中可以看出，初始方案中的定位力主要有2次和4次分量，经过优化后，2次分量和4次分量被很大程度地削弱，但6次分量有了一定的增加。

4 实验验证

根据优化方案设计并制作了样机如图9所示。测量定位力时，采用变频器驱动旋转异步电机带动蜗杆推动永磁直线电机铁心低速平稳运动，通过控制器显示的光栅读数标定1个极距内40个等距测量点，通过拉力传感器记录测量点拉力值，测量结果如图10所示。在永磁直线电机平稳低速运动过程中采用示波器记录三相绕组的反电势波形。

图9 扁平永磁同步直线电机实验样机

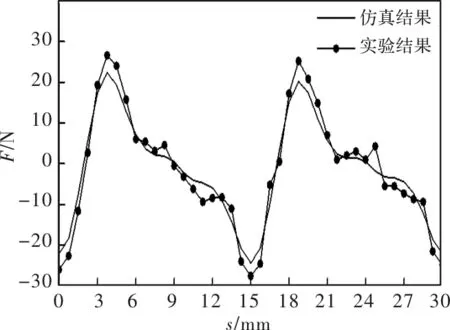
图10 样机定位力波形

从图10可知，有限元仿真结果与实验结果基本一致，但由于机械结构及样机材料等因素的影响，使得结果存在着一定的误差。定义永磁直线电机的电压常量为反电势幅值与速度的比值。通过反电势波形可以得到反电势幅值和频率，并根据速度公式v=2f可计算出速度。根据仿真波形计算得到的电压常量为88.43V·s/m，根据实验波形计算得到电压常量为90.24V·s/m，两者的误差为2%。

5 结 语

本文从永磁直线电机的结构入手解析了定位力的组成，并分析了影响端部力和齿槽力的关键参数。以1台18槽21极永磁电机为优化对象，通过对有限元物理模型的处理，将端部力与齿槽力进行分离，通过对分析得到齿槽力可以削弱端部力，使得两者叠加后的定位力小于端部力。然后结合田口法和有限元法，以边齿宽度、斜极长度、磁钢宽度和磁钢厚度为优化变量，以定位力、反电势和磁钢用量为优化目标进行优化，仿真结果表明优化后的定位力减小、反电势增大、磁钢用量减小，实现了优化目标。最后，根据优化参数制作了样机，通过对样机的定位力与反电势的测试来证明了优化方法的有效性。研究结果对扁平永磁直线电机工程设计和应用具有指导意义。