一种矩形板四足驱动旋转超声波电机的设计与仿真

刘佩珊，张 锦,2，殷玉枫，高崇仁，吉正杰，冯毅杰

(1.太原科技大学 机械工程学院，太原 030024；2.山西交通职业技术学院，太原 030031)

0 引 言

在近代尖端工业生产领域、科学研究领域以及航空航天等领域，精密机构占有着极其重要的地位，而压电式微型电机是精密机构能在各种工况下正常运行的关键要素，超声波电机(USM)也被称为新一代电机[1]。超声波电机是利用压电材料的逆压电效应激励固定在电机定子上的压电陶瓷片，使得定子组件在超声波频域范围内产生机械振动或准静态变形，利用共振原理将定子的微变形放大，并利用摩擦将电能耦合成驱动转子运动的机械能，超声波电机具有低速转矩大、结构简单、单位重量输出功率大、无电磁干扰等特点[2]。超声波电机多应用于精密仪器，如数码相机、手机、航天航空等。

国内外对超声波电机的研究取得了一定进展，但对旋转型超声波电机的研究较少，而运转速度较低、承载能力不足、加工成本较高、结构较复杂也是目前旋转式超声电机存在的问题[3]。2017年丰桥技术科技大学的Tomoaki设计了一种扭矩超过10μNm并拥有微型弹簧预紧机构的微型超声马达[4]。2016年潘巧生提出了一种基于偏心轮受迫振动的压电马达，利用了偏心轮的受迫振动馈入压电堆叠实现了应用飞轮储能的想法[5]。2015年周茂瑛设计了一种基于压电振动的微型旋转马达，运用了尺蠖的运动仿生设计，结构简单但位移精度和响应时间都较小[6]。2014年S.K.Cheon等人设计了一种空心盘式超声电机，为了增加定、转子之间的接触点，设计了一种具有16个接触点的六边形电机，最大位移发生在53.2kHz谐振频率，最大转速为115r/min，最大转矩为1.4×10-5N.m[7]。

本文利用压电陶瓷片的d31横向振动模态激励压电陶瓷产生横向收缩，激发定子产生变形，并驱动四个驱动足端面产生椭圆轨迹的运动，经摩擦推动转子做连续旋转运动。定子采用贴片式结构，为超声波电机的小型化提供了思路。本文优化了电机定子结构，利用有限元法对优化后的超声波电机定子部分进行了模态分析，提取到了能够激励驱动足端面产生椭圆运动的谐振频率，在该谐振频率下利用Ansys的瞬态分析模块对电机定子部分的驱动周期和驱动足的运动轨迹进行了分析。

1 构造机理

图1为四足驱动矩形旋转超声波电机几何模型，该电机由定子、压电陶瓷片、转子、主轴、轴承、弹簧、螺母组成。在中空矩形弹性体上表面焊接有4个驱动足，驱动足能起到放大中空矩形弹性体变形的作用，在转子外表面和定子驱动足接触区黏贴摩擦材料。螺母和弹簧构成超声波电机定子组件与转子之间的预压力调整机构。

图2为定子三维结构图，四片压电陶瓷片使用导电环氧胶粘贴于弹性体表面，压电陶瓷片与弹性体粘结的表面接地，另一表面连接图示驱动电源，图中箭头表示了压电陶瓷的极化方向。定子弹性体采用弹簧钢，压电陶瓷片材料为pzt-8，压电材料pzt-8的各项参数如表1所示。

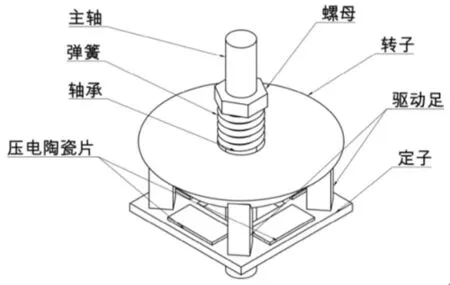
图1 电机结构图

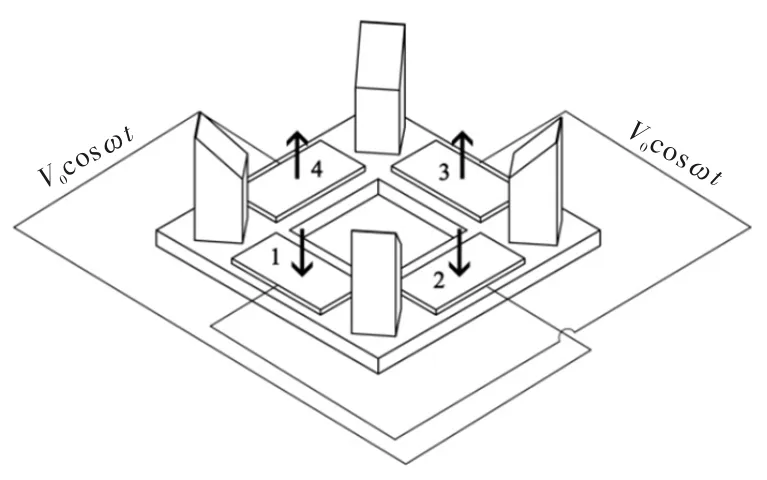
图2 极化方向与施加激励信号方式

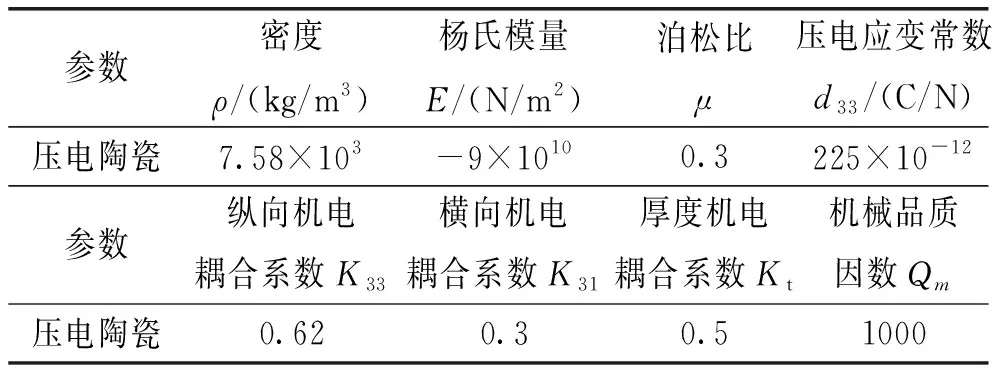
参数密度ρ/(kg/m3)杨氏模量E/(N/m2)泊松比μ压电应变常数d33/(C/N)压电陶瓷7.58×103-9×10100.3225×10-12参数纵向机电耦合系数K33横向机电耦合系数K31厚度机电耦合系数Kt机械品质因数Qm压电陶瓷0.620.30.51000

2 驱动原理

对于经过极化处理的压电陶瓷片，压电应变常数矩阵d的分量分为3个非零分量d33，d31，d15[8]。本文提出的超声波电机中，粘贴于定子基座上的压电陶瓷片工作在d31横向振动模态。驱动信号按一定相位差作用于对称的两组压电陶瓷片上表面(如图2所示，箭头代表压电陶瓷片的极化方向)，压电陶瓷片与弹性体粘结的表面接地。在逆压电效应作用下，压电陶瓷片的横向振动模态驱动超声波电机定子上端的驱动足端面产生椭圆轨迹运动，并通过定子与转子之间的多接触面摩擦耦合推动转子旋转，实现制动。

四足驱动超声波电机的定子组件由一个固定有四片压电陶瓷片的中空矩形板和四个驱动足组成，四个驱动足固定于板的四个角上。当在四片压电陶瓷片上施加如图2所示的电压时，中空薄矩形板将产生变形,激发四个驱动足端面X、Y、Z相振幅，再通过摩擦耦合驱动转子旋转。压电陶瓷片1和压电陶瓷片3施加V0sinωt激励电压，压电陶瓷片2和压电陶瓷片4施加V0cosωt激励电压，为了更直观地理解超声波电机的驱动原理t0，将每个振动变形过程分为如图3所示的四个子部。

图3 定子组件一个周期的运动

(1)相角ωt=0，压电陶瓷片3伸长，压电陶瓷片1收缩，其他两个压电陶瓷片保持不变，此时各驱动足的位移如图3(1)所示。

(2)相角ωt=π/2，压电陶瓷片2伸长，压电陶瓷片4收缩，其他两个压电陶瓷片保持不变，此时各驱动足的位移如图3(2)所示。

(3)相角ωt=π，压电陶瓷片1伸长，压电陶瓷片3收缩，其他两个压电陶瓷片保持不变，此时各驱动足的位移如图3(3)所示。

(4)相角ωt=3π/2，压电陶瓷片4伸长，压电陶瓷片2收缩，其他两个压电陶瓷片保持不变，此时各驱动足的位移如图3(4)所示。

以上是定子组件的一个工作周期，可以得出，通过将两个不同的振动进行叠加，每个驱动足端面均形成一个完整的三维椭圆轨迹，如果连续激发图3所示的驱动信号，将使每个驱动足端面产生连续的三维椭圆运动，进而经摩擦耦合驱动转子连续顺时针旋转。在将两相交流激励电压交换施加后，转子将产生逆时针旋转运动。

3 定子组件优化设计

3.1 驱动足结构中心与定子结构中心距离d

驱动足具有放大矩形板振幅的作用，故驱动足结构中心与定子结构中心的距离d对超声波电机的性能影响较大，现取驱动足A端面的中心点作为研究质点(图2所示)，取距离为15mm～28mm，步长为1mm，按图2所示施加幅值为20Vp-p的交变电压作为激励信号，得到图4所示驱动足结构中心与定子结构中心的距离d与驱动足A端面的中心点振幅的关系。

图4 驱动足中心与定子结构中心距离d与振幅关系

可以看出，在距离d为17mm～28mm的范围内驱动足A端面的中心点振幅呈上升趋势，但变化不明显，为保证结构稳定性及考虑便于加工等方面，取d=25mm进行设计。

3.2 中空矩形板厚度h

中空矩形板作为定子的基座，其厚度对定子的固有频率影响较大，为了激发驱动足端面的椭圆运动，由于小于1mm的板厚无法激发出超声波电机所需要的弯振，故取中空板厚h为1mm～3mm，步长为0.2mm进行模态分析，选取中空矩形板定子二阶面内弯振振模态频率绘制曲线。

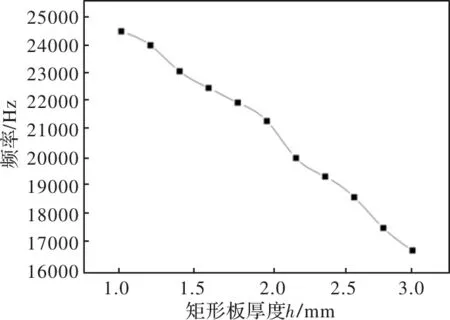
图5 中空矩形板厚度h与二阶面内弯振模态频率关系

由图5可以看出，矩形板二阶面内弯振模态频率随着矩形板厚h的增大而减小，考虑到超声波电机的工作频率在超声范围内，同时考虑定子组件稳定性以及电机的尺寸，选取h=1.5mm进行设计。

4 优化后定子有限元建模及模态分析

四足驱动矩形板旋转超声波电机有必要研究中空矩形板的固有振动特性。首先在板上取一微元体进行受力分析，得到板的自由振动微分方程

设板外表面的固有振动位移为

w=w(x,y,z)=φ(x,y)q(t)

板的四边均简支，L1为中空矩形板的边长，L2为中空矩形板中空部分的边长(如图4所示),可得到四边简支中空矩形板的固有频率

m,n=1,2,…,∞

超声波电机驱动原理是利用向沿纵向极化的压电陶瓷片加载两相激励电压，激发压电陶瓷片的d31横向振动模式，压电陶瓷片与中空矩形板通过导电环氧胶粘贴固定，使中空矩形板发生形变，通过叠加两个不同的振动驱动定子上表面的驱动足端面产生三维椭圆运动，进而驱动转子旋转。定子结构模型如图6所示，定子结构的各参数如表2所示，为了便于建模，假设金属弹性体材质均匀，采用有限元软件Ansys对定子建模，并利用Block lancos法对定子进行模态分析，指定模态提取频率范围为18kHz～25kHz，得到定子的固有振型和模态频率。

图6 定子结构图

L1/mmL2/mmL3/mmL4/mmL5/mmL6/mm5030772012.5l1/mml2/mmø1/mmα/(°)h/mm5103.51351.5

图7 定子四阶固有振动云图

如果激励信号的频率与定子的某阶固有振动趋近时，可以激发定子的这一阶的振动，使驱动足端面产生椭圆运动，进而驱动转子旋转。图7为定子的四阶固有振动云图。当模态频率为22244Hz时激励出矩形板的一阶面外振动，进而激发驱动足端面的三维椭圆运动。

5 定子组件瞬态分析

根据电机各部件及材料参数进行有限元三维建模，利用有限元软件Ansys对超声波电机的定子组件进行模态计算，定子组件整体建模如图8所示，整体模型有2644个单元，15956个节点。压电陶瓷片两端根据图2所示施加幅值为20Vp-p的交变电压作为激励信号，设置驱动频率为22.244kHz，由瞬态分析提取到定子一个激励周期的工作模态如图9所示。图中箭头表示一个周期内的定子的运动方向。

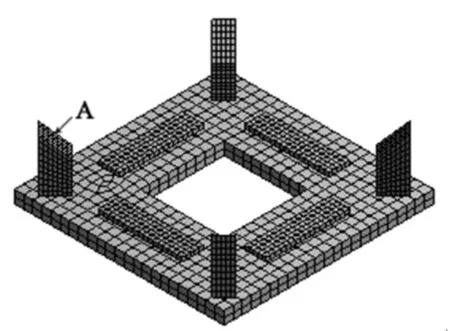
图8 定子组件有限元模型

图9 定子组件一个周期的工作模态

图9为定子组件的四个驱动足端面在一个周期中的运动轨迹，在压电陶瓷片上施加交变电压时，压电陶瓷片工作在d31横向振动模态，随着压电陶瓷片的伸缩运动激发定子组件的驱动足产生椭圆运动，通过摩擦耦合推动转子旋转。

在一个运动周期中取65个节点对质点的运动轨迹进行仿真，驱动足端面质点的运动轨迹三维曲线如图10所示。可以看出，质点在三维空间里的运动是椭圆轨迹。当四个驱动足同时产生具有π/4周期相位差的椭圆运动，将驱动转子实现旋转运动。

图10 驱动足A中心质点的三维空间轨迹

6 结 论

本文提出了一种贴片式四足驱动旋转超声波电机，将四片沿厚度极化的压电陶瓷粘贴于定子上表面，施加两相交流电激励压电片产生d31横向振动模态，并激发驱动足端面产生椭圆运动轨迹，进而驱动转子旋转。该模型结构简单、便于加工。

(1)对定子进行优化设计，结果表明：驱动足结构中心与定子结构中心距离d=25mm，矩形板厚h=1.5mm时，可以在便于加工和保证结构稳定性的前提下，确保定子组件的性能指标。仿真提取到模态频率为22244Hz时可以激励出矩形板满足电机要求的一阶面外振动。

(2)输入20Vp-p的交变电压作为激励信号，设置驱动频率为22.244kHz，通过瞬态分析得到了定子组件一个周期的运动模态，同时得到驱动足的振幅达8μm，验证了该模型的有效性。

(3)四足驱动超声波电机采用贴片式定子，不仅减小了定子组件加工、装配难度，还能提供有效的振动模态，达到驱动转子连续旋转的设计要求，同时也为超声波电机的微型化提供了思路。