初中数学前置性补偿教学内容的设计

王天龙

摘要：前置性补偿教学是指在正式课堂教学前，让学生根据已有的知识和经验进行目标明确的自主练习，而教师通过巡视、批阅及时发现并解决学生存在的问题的一种教学方式。初中数学教学中，可以针对不同的课型，根据不同的导向，在学习单中灵活设计“前置性补偿”内容，并以此展开前置性补偿教学：新授课的导向是关联，习题课的导向是冲突，复习课的导向是唤醒，活动课的导向是体验。

关键词：前置性补偿教学 初中数学 内容设计 课型

笔者所在学校是一所“新优质初中”，学生以学区生为主，部分为外来务工人员子女。他们的知识基础、认知水平参差不齐，而且自主学习能力比较欠缺，学习习惯和方法普遍不佳。为了充分落实“以学定教”的理念，提高学生的自主学习能力，我校成功立项了省级课题“基于目标的前置性补偿教学的实践研究”。笔者作为核心成员参与了课题研究。目前的研究思路是結合数学学科特点，在学习单中设置相应内容，开展前置性补偿教学。本文谈一谈笔者的思考与实践。

一、前置性补偿教学的内涵与价值

前置性补偿教学与课前预习有所区别，是指在正式课堂教学前，让学生根据已有的知识和经验进行目标明确的自主练习，而教师通过巡视、批阅及时发现并解决学生存在的问题的一种教学方式。

一方面，前置性补偿教学发生在课堂的前几分钟，能够减轻学生的课后负担，促进学生的课堂思考，也有利于教师了解学生的学习情况，做出有针对性的指导。另一方面，前置性补偿教学让学生“先做后学”，从已有的知识和经验中启发联想，获得初步感受和体验，激发学习兴趣，领悟学习方法，为后续课堂教学做铺垫。在笔者近两年的探索实践中，前置性补偿教学的引入使得学生尤其是“学困生”的数学成绩有了明显的提升：笔者所教班级差分率明显下降，合格率显著上升。

二、前置性补偿教学内容的设计

教学实践中，笔者针对不同的课型，根据不同的导向，在学习单中灵活设计“前置性补偿”内容，并以此展开前置性补偿教学。

（一）新授课：导向“关联”

新授课的前置性补偿教学，可以通过学习单上的问题，帮助学生建立起已有知识和即将学习的知识之间的关联，从而触类旁通，建构新知。

例如，苏科版初中数学七年级下册《10.1二元一次方程》新授课学习单中的“前置性补偿”内容设计如下：

问题1：你能写出一个一元一次方程吗？

问题2：你能用自己的语言写出一元一次方程的定义吗？

问题3：3x-2y=1还是不是一元一次方程？

问题4：你还能写出和3x-2y=1相似的等式吗？

问题5：你能不能给这类等式起个名字？简单解释一下为什么这么叫？

……

学习二元一次方程之前，学生已经学过一元一次方程。一元一次方程和二元一次方程存在很多关联，而关联的桥梁就是“元”“次”和“方程”这三个关键词。这里的前两个问题就是关于一元一次方程的。问题1让学生写出一元一次方程的例子，为学生回忆相应的定义做铺垫。问题2让学生写出一元一次方程的定义，就是让学生回忆起“元”“次”和“方程”分别是什么：“元”是未知数，“次”是未知数最高的次数，“方程”指的是等式。有了这样的回顾之后，出示问题3，让学生判断新的方程，学生就可以迅速判断出3x-2y=1这个等式不是一元一次方程。问题4让学生仿写新的方程，学生在修改x和y的系数后都能够写出相应的方程。顺其自然，问题5让学生给新的方程起名字并做解释，学生就能够依据“元”“次”和“方程”这三个关键词，得到二元一次方程的概念。这样，从一元一次方程出发，通过关联，顺利地让学生初步认识了二元一次方程。

（二）习题课：导向“冲突”

习题课的前置性补偿教学，可以通过学习单上的个别练习，设置与新授知识相矛盾的内容，激发学生的认知冲突，使学生对已有知识产生新的认识。

例如，苏科版初中数学七年级下册《9.5多项式的因式分解》习题课学习单中的“前置性补偿”内容设计如下：

因式分解下列多项式：

1.x²-4y²;

2.2x²-4x+2;

3.拓展延伸：（3x-2）²-（x+4）²。

……

在新授课上，学生知道：把一个多项式因式分解，应该先提公因式，再运用公式，最后检查有没有把每个因式都分解到不能再分解。这里的前两题比较简单，利用这三个步骤很容易解决。但是，最后一题难度有点大。学生可能这样解决：发现没有公因式可以提，就整体套用平方差公式得到（3x-2）²-（x+4）²=（3x-2+x+4）（3x-2-x-4）=（4x+2）（2x-6）;检查发现两个因式都是一次式，不能再套用公式分解了，就认为做完了。也可能这样解决：把两个平方式展开、合并后提公因式，得到（3x-2）²-（x+4）²=8x²-20x-12=4（2x²-5x-3）;检查发现虽然是二次式，但是不符合平方差和完全平方的形式，所以不能再分解了，认为做完了。两种做法思路都正确，过程也正确，但是结果不同，并且都不是正确答案。这样，学生的认知冲突就产生了。教师可以引导学生分析原因，提升认识，解决冲突：第一种做法中，一开始没有公因式可以提，不代表套用公式之后也没有公因式可以提，所以在检查分解是否彻底时，还需要考虑能否提公因式和运用公式;第二种做法中，得到的二次式不符合平方差和完全平方的形式，不代表不能分解，实际上可以先凑成完全平方的形式，再得到平方差的形式（教师甚至可以简单介绍“十字相乘法”）。

（三）复习课：导向“唤醒”

复习课的前置性补偿教学，可以通过学习单的练习，唤醒学生对已学知识的记忆，从而巩固所学，厘清认识。

例如，苏科版初中数学七年级下册第8章《幂的运算》复习课学习单中的“前置性补偿”内容设计如下：

计算：

1.（-2）²×2²×（-2²）;

2.（-2）¹⁰×2¹⁰×（-2¹⁰）;

3.3^-2+（π-3）⁰;

4.（2/3）^-2×（3/2）²。

……

这里，前两题除了指数不同之外，其余部分都一样，旨在唤醒学生对同底数幂乘法的运算性质以及底数为负数、幂取相反数时的处理方法的记忆。第1题为第2题做铺垫：第1题的指数相对较小，不用幂的运算性质而分别算出每个幂的值，也可以算出来;第2题就必须利用幂的运算性质来计算，“死算”非常麻烦。第3题比较容易，旨在唤醒学生对负指数和零指数计算方法的记忆。第4题则让学生综合运用负指数的计算方法和同底数幂乘法的运算性质。这道题有一定的陷阱：学生容易直接利用同底数幂乘法的运算性质把指数加在一起，或者直接利用积的乘方的运算性质把底数乘在一起。如果学生出现这样的错误，则说明学生对幂的运算性质记忆不清，需要教师及时进行补偿教学。

（四）活动课：导向“体验”

活动课的前置性补偿教学，可以通过学习单的活动任务，引领学生操作体验，探索获得初步的知识，或者解决简单的问题。

例如，苏科版初中数学八年级上册第1章的《数学活动关于三角形全等的条件》一课学习单中的“前置性补偿”内容设计如下：

活动1：在草稿纸上画出△ABC，其中∠A=45°，AB=3cm，AC=4cm。剪下此三角形，和你的小伙伴比一比，它們全等吗？

活动2：在草稿纸上画一个三角形，使得其中一个角为45°，两条边长分别为3cm、4cm。这个三角形和活动1中的三角形一定全等吗？

活动3：在草稿纸上画出△ABC，其中AB=3cm，∠A=45°，∠B=30°。剪下此三角形，和你的小伙伴比一比，它们全等吗？

活动4：在草稿纸上画一个三角形，使得其中两个角分别为45°、30°，一条边长为3cm。这个三角形和活动3中的三角形一定全等吗？

反思：通过这4个活动，你有什么发现？

……

在这一系列活动中，学生首先能体验到角的画法的多样性：可以利用量角器、三角板或折纸。其次能体验到分类讨论的数学思想，加深对全等三角形判定条件的认识：

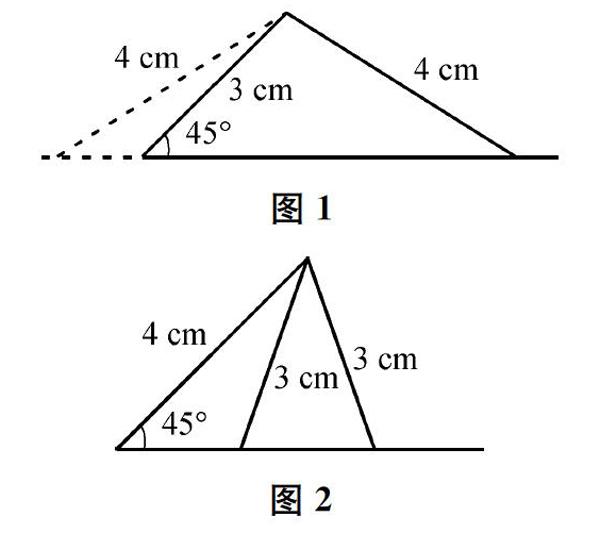
活动1和活动2都是给定“两边一角”，画三角形。活动1给定的“两边一角”关系确定，因此学生画出的三角形是全等的，由此学生可以体会到“SAS”可以判定三角形全等的基本事实。活动2给定的“两边一角”关系不确定，可以分为“SAS”和“SSA”两种情况，而“SSA”又可以分为“S1S2A”和“S2S1A”两种情况，由此学生可以进一步体会到“SSA”有时可以判定三角形全等（如图1），有时不行（如图2），一共可以画出3种不同的三角形。

活动3和活动4都是给定“两角一边”，画三角形。活动3给定的“两角一边”关系确定，因此学生画出的三角形是全等的，由此学生可以体会到“ASA”可以判定三角形全等的基本事实。活动4给定的“两角一边”关系不确定，可以分为“ASA”和“AAS”两种情况，而“AAS”又可以分为“A1A2S”和“A2A1S”两种情况，由此学生可以进一步体会到“AAS”可以转化为“ASA”，从而判定三角形全等，一共可以画出2种不同的三角形。