数学问题解答

2020年2月号问题解答

(解答由问题提供人给出)

2526在四边形ABCD中，E是边CD上一点，BE与AC交于点F，射线DF交BC于点G.R是AB延长线上一点，射线RG交CF于点P，AE与PD交于点H.证明：R、F、H三点共线.

(重庆市合川太和中学 袁安全 401555)

证明如图所示，设直线HF分别交直线AB、PG于点R1、R2,则欲证R、F、H三点共线，

事实上，由面积关系可得

=1.

故原问题获证.

2527在△ABC中，求证:

(陕西省咸阳师范学院基础教育课程研究中心 安振平 712000 )

证明注意到△ABC中的恒等式:

=1.

则x,y,z>0,xy+yz+zx=1.

应用三角公式和柯西不等式，得

将以上三式相加，并注意到xy+yz+zx=1,立得

注意到常见不等式

不妨设sinA≥sinB≥sinC,则

应用切比雪夫不等式，得

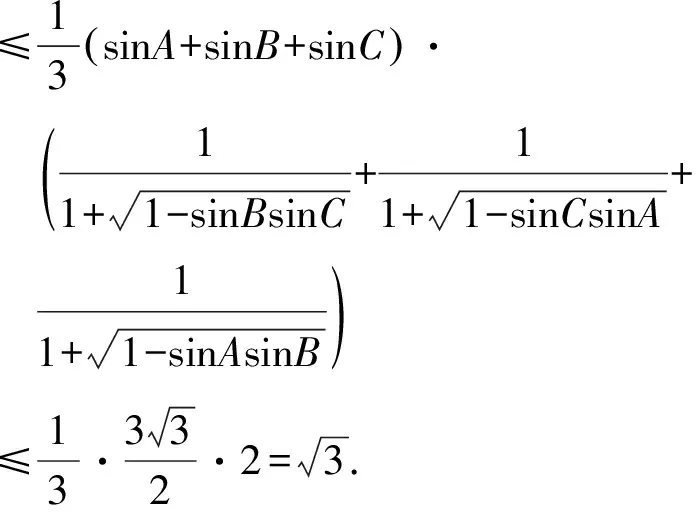
2528试证明tan27°=sec36°-tan36°.

(安徽省六安第二中学 陶兴红 237005 )

证明因为tan27°·tan63°=1,

所以tan27°·tan(27°+36°)=1,

所以tan27°(tan27°+tan36°)=1-tan27°tan36°,

所以tan227°+2tan36°tan27°-1=0,

所以由求根公式得

=sec36°-tan36°.

所以问题得证.

(浙江省慈溪市慈溪实验中学 华漫天 315300)

证明作EG⊥AD于G，FH⊥AD于H，分别延长AB、FH交于点I.

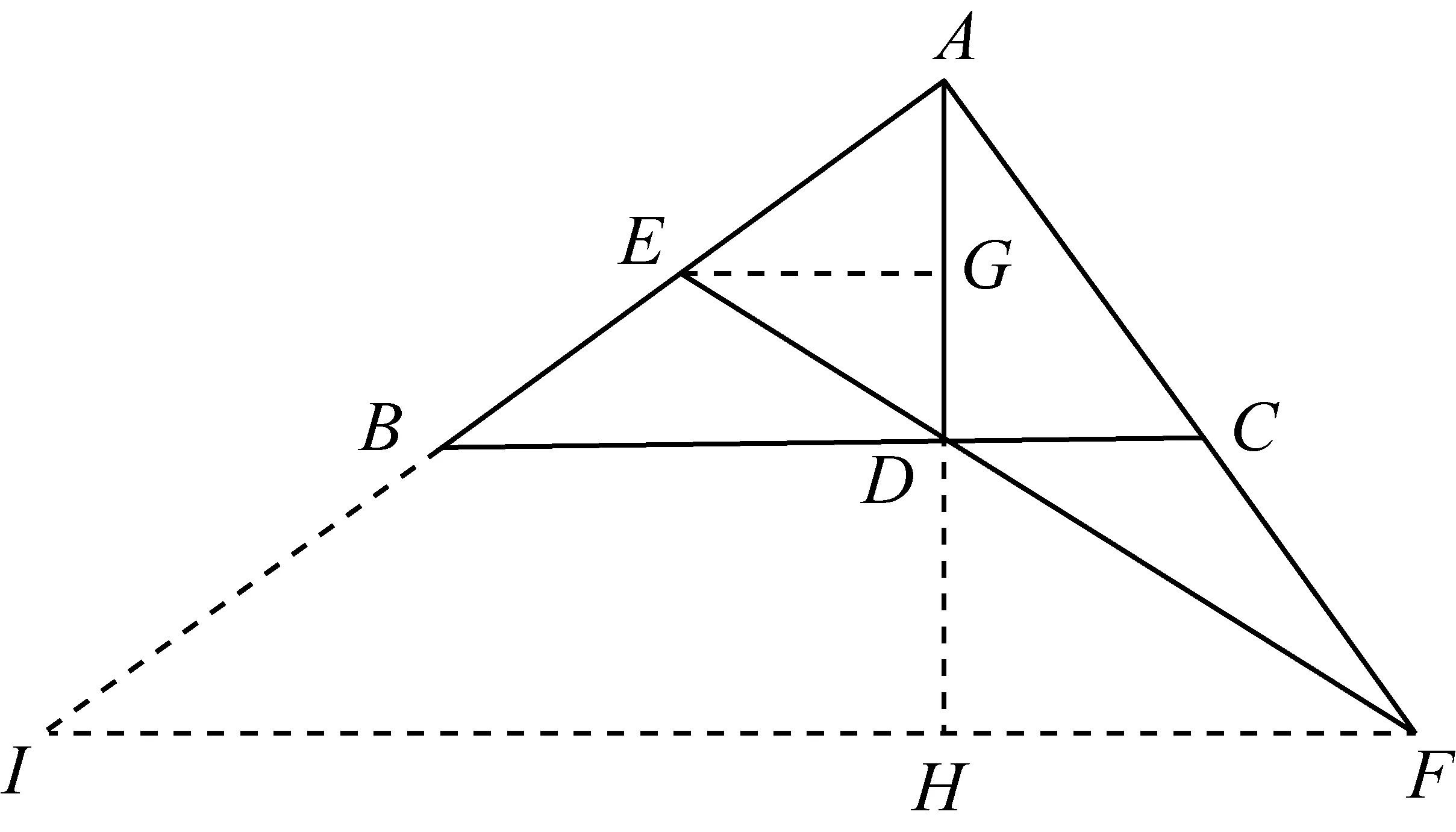
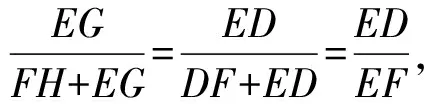
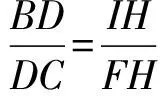
代入上式得

下证原命题.

易得△AEG∽△CBA，得AE·AB=BC·EG，由△AFH∽△BCA，得AF·AC=BC·FH，所以

2530已知a,b,c∈[-2,2],a+b+c=0，求a3+b3+c3的最大值.

(四川省成都华西中学 张云华 610051)

解因为a∈[-2,2],所以a3-(3a+2)=(a+1)2(a-2)≤0,所以a3≤3a+2,同理,b3≤3b+2,c3≤3c+2,a3+b3+c3≤(3a+2)+(3b+2)+(3c+2)=3(a+b+c)+6=6,且当a=2,b=c=-1,或b=2,a=c=-1,或c=2,a=b=-1时,a3+b3+c3=6,故a3+b3+c3的最大值为6.

2020年3月号问题

(来稿请注明出处——编者)

2531设两个正数x,y满足xy=1,求证:

①

(天津水运高级技工学校 黄兆麟 300456)

2532如图，已知梯形ABCD，且△ABC为等腰直角三角形，作PD⊥BD、QD⊥DC且△PDB∽△QDC，PM⊥AD，R为PQ中点，求证：AB∥RM.

(江西师范高等专科学校 王建荣 335000)

2533已知在锐角△ABC中，a2cosBcosC=

9bccos2A,求cos3A的取值范围.

(安徽省六安第二中学 陶兴红 237005)

2534已知抛物线Γ：y=ax2+bx+c，(a≠0). ⊙O：x2+y2=r2(r>0).在抛物线Γ上任取三点A、B、C， 若直线AB、AC均与⊙O相切，则直线BC也与⊙O相切的充要条件为

(浙江台州市洪家中学 邬天泉 318015)

2535已知a，b，c>0，求证：

(河南省南阳师范学院软件学院 李居之 孙文雪 473061)