核心素养：教学的第三条主线①

渠东剑

(南京市秦淮区教师发展中心 南京市高中数学渠东剑名师工作室 210002)

1 问题的提出

一般认为，数学教学有两条主线：知识主线与方法主线．其中知识主线是明线，即教学要突出知识发生发展的过程，体现知识的来龙去脉；方法主线是暗线，思想方法蕴藏于数学知识的发生发展过程之中，被誉为数学知识的精髓，数学的灵魂，需要教师挖掘、提炼并贯穿到知识的教学中去[1]．当下，《普通高中数学课程标准(2017年版)》(以下简称《课标》)提出了数学学科核心素养(以下简称核心素养)，那么，它对教学实践将产生怎样的影响？它与原有的上述两条主线有何关系？或者说，在教学实践层面，我们应该如何去主动落实《课标》精神，努力发展学生的核心素养呢？

发展学生核心素养是课程总目标，一定意义下是长远目标．核心素养的养成是日积月累的结果，基于核心素养的教学需要整体设计、分步实施，[2]《课标》也倡导主题(单元)教学设计．但是，从另一个角度说，课堂是教学的主阵地，教学实施是通过具体的一课时一课时地去完成的．可以说课时教学是组成教学实施的基本单位．那么，就核心素养目标的达成而言，每一节课都应为形成和发展核心素养作出可能的贡献．这也就可以认为，每一课时都应该在核心素养的引导下，去实施教学．从而，探讨核心素养导向下的课时教学，无论是理论层面，还是就实践需求，无疑具有重要的意义．

基于此，就课时教学实践而言，本文拟在已有上述两主条线的基础上，探索核心素养下的课时教学，并将以“平面向量基本定理”的教学为例说明．笔者的观点是，核心素养是教学的第三条主线——素养眼线，起教学向导的作用．眼线，这里取 “暗中侦察情况、必要时担任向导”之意(据《现代汉语词典(第6版)》)．这样，就将形成数学教学的三条主线，并且三条主线之间的关系是，突出知识明线，看重方法暗线，看见素养眼线．

2 核心素养：教学的第三条主线

核心素养应当成为教学的第三条主线：教学的眼线．教学把准三条主线有两层涵义．第一，教学设计要高屋建瓴：以核心素养为导向，以思想方法为重点，以知识落实为载体．第二，教学实践要扎扎实实：以知识为根基，以思想方法为主干，以核心素养为目标．

2.1 从课程目标认识

根据课程目标，通过高中数学课程的学习，学生能获得发展所必需的“四基”；进而，提高“四能”，发展核心素养，终极目标或外在表现是“三会”．形成和发展核心素养的本源是知识[3]，不突出知识的教学，发展核心素养的目标终将落空．

反过来，“学科核心素养是学生通过学科学习而逐步形成的……”[4]核心素养综合地体现在 “发现和提出问题、分析和解决问题”的过程中；提高“四能”离不开“四基”，或者说“四能”是在“四基”的基础上发展起来的．例如，“发现问题”的能力，就要在情境中用“数学的眼光”去观察并发现问题，进而形成更高境界的“数学的眼光”、更高层次的“发现问题”的能力．这就是说，要形成和发展核心素养，就要落实“四基”，进而提高“四能”；落实“四基”就意味着要突出知识与思想方法，因为“四基”本身就包含基础知识、基本思想方法；甚至知识本身就蕴含着方法，脱离知识的所谓思想方法是不存在的．笔者试图以框图描述这三条主线与“课程”、“四基”、“四能”、核心素养与“三会”之间的关系，如图1．

图1 教学三条主线的关系

2.2 从知识与能力关系理解

综观知识与能力熟重熟轻的历史纷争，人们愈加认识到二者对立统一的关系，知识是生成能力的本源，已成为一个基本的命题．[3]首先，知识本身就包含陈述性知识与程序性知识，一定意义下，程序性知识就是思想方法；其次，由知识学习转化而来的能力，又将对知识的学习与运用，产生积极的促进作用；再次，这种由知识学习转化而来的能力，其实蕴含着思维习惯和方法，这其实就是核心素养．[2]所以，教学突出知识主线，以知识发生发展的过程为基本线索，是培养能力、落实核心素养目标所必须的．

2.3 从三主条线内涵去考量

其一，看见眼线，意味着核心素养应当成为教学的向导．相对于具体的、显现的知识与技能、思想与方法而言，核心素养处于更上位层次．它不仅包含知识技能、思想方法，还有情感、态度与价值观的内涵．看见眼线，就是要心中有核心素养目标，以核心素养为向导，去引领教学的实践．

其二，看重暗线，就是仍然要注重数学思想方法．知识是显性而具体的，蕴含在知识中的思想方法是数学的本质，也是数学育人的根本．一定意义下，数学思想方法既是核心素养的重要内容，又是发展核心素养的依托．因而，教学实践中应充分挖掘知识发生发展过程中的思想方法，并有意渗透到教学过程中去．这是每一节课都需要努力而为之的，而且要有高度的自觉与积极的主动性．

其三，突出明线，即突出知识的来龙去脉，突出知识发生发展的过程．教学要以知识为载体，以问题为导向，以解决问题为动力，以知识发生发展的逻辑过程为基本线索展开，使知识的教学，成为在教师的指导下，学生不断发现和提出问题、分析和解决问题的过程；使学生的学习成为数学再发现、再创造的过程，让知识从学生的头脑中自然流淌出来．

具体地，不断地发现和提出问题、分析和解决问题，就是要让课堂教学“问题结构”化：学习从问题情境开始，这个情境可以是生活情境、数学情境或科学情境；教学就是基于情境，启发学生发现并提出问题；面对提出的问题，就要分析与解决问题；解决后的问题，又成为新的情境，(这个情境大多属于数学情境)基于数学“进一步”研究的需要，又将提出新的问题；面对这个新的问题，又要分析与解决问题……这就是依托知识发生发展的线索，不断发现与提出问题、分析与解决问题的过程．进而，基于这样的教学过程，形成和发展学生的核心素养．

3 基于三条主线的教学设计举例

平面向量基本定理是“平面向量”中的一条重要定理，冠有“基本”二字，足见其基础性、发展性与核心地位．这里，将基于上述三条主线视角，分析教学内容、尝试设计教学，探索基于三条主线下的教学实践．

为叙述方便，这里先将平面向量基本定理抄录如下：

如果e1,e2是同一个平面内两个不共线的向量，那么对于这一平面内的任一向量a，有且只有一对实数λ1,λ2，使a=λ1e1+λ2e2．

3.1 基于三条主线的内容分析

3.1.1知识主线

第一，分析教材“平面向量”知识发展的脉络．平面向量基本定理位于向量的概念、向量的运算(加法、减法、数乘)之后 ，后续内容则是平面向量的坐标表示、坐标形式下的向量运算(加法、减法、数乘、数量积)．之前的平面向量用有向线段表示，其运算形式(例如向量加法的平行四边形法则)属于几何范畴．也就是说，向量兼有数与形双重特征，但平面向量基本定理之前的内容侧重于几何特征背景下的研究．即使是向量的数量积，也完全可以放在平面向量基本定理之前．基于此，我们似乎可以更清楚地看出本章的知识发展脉络，如图2：

图2 平面向量知识线路图

进而，寻求平面向量的代数形式，并基于代数形式研究其运算，(这正是数学研究代数对象的重要手段)就成为自然而必要的了．显然，平面向量基本定理是探索其代数形式的基础．在确定的一组基底之下，向量的本质就是有序实数对，这其实已经是仿射坐标的意义了．从这一点来说，平面向量基本定理是探索向量代数形式表示、并基于代数形式研究平面向量运算的基础．

第二，一定意义下，向量共线定理的本质是，直线是一维的，研究了两个向量共线，也就同时研究了两个向量的不共线．平面向量基本定理的本质是，平面是二维的．若以基底“生长”的视角分析，{λ1e1+λ2e2}(λ1,λ2∈R，e1,e2是不共线的向量 )可以“生成”平面内的任一向量．换言之，平面内的任意三个向量必线性相关．由此说开去，空间向量基本定理表明空间是三维的，后续n维线性空间中的极大无关组……都可以看成向量共线定理、平面向量基本定理、空间向量基本定理的推广与发展．所以，突出平面是二维的本质，是平面向量基本定理教学过程中所不容忽视的．

第三，在平面向量基本定理中，两个实数λ1,λ2有三个要素：一是存在，二是有序，三是唯一．平面向量基本定理的探索过程可以分为两部分：一是基于平行四边形法则，将一个向量在两个方向(基底)上“分解”；二是在分解后利用向量共线定理去探寻λ1,λ2．存在性可以从“作图”(几何分解)与应用向量共线定理的过程去理解，而唯一性似乎不容易做到严密论证——这里的几何作图过程，一定意义下是归纳推理，不可能穷尽所有情形，因而也就不能作为严密的推理过程．

基于此，教学中似乎应该让学生充分经历“作图”的过程，包括选择一些可能的情形去验证，比如向量a为零向量、与一个基向量共线，等等．在作图实施分解的过程中达到心理认可，即这样的分解是可能的，有序实数对λ1,λ2是存在的；体验“分解”的结果应当是唯一的，也就是认同有序实数对λ1,λ2是唯一的．让学生心理认同平面向量基本定理，也许就达到了教学要求．

3.1.2方法主线

平面向量基本定理及其建立过程，蕴含了诸多数学思想方法，要在建构平面向量基本定理的教学过程中，也就是在知识发生发展的过程中，有意渗透，着力突出的．

其一，数形结合思想方法：平面向量基本定理的探索过程应该是依据平行四边形法则，从几何图形出发，得到在两个向量(基底)方向上的分解，这属于“形”的范畴；然后利用向量共线定理，得到有序实数对λ1,λ2，这是数形结合的结果．其二，化归转化思想方法：依据平面向量基本定理，在确定一组基底的条件下，平面内的任一向量都可以用这一组基底线性表示，而且表示是唯一的；在此意义下，平面内的所有向量，都可以转化为这一组基底去研究．其三，有限与无限思想：用有限刻画无限，在平面向量基本定理的意义下，平面内任意两个向量之间的“差异”，本质上就是这一有序实数对的不同．其四，变与不变思想：当一组基底确定后，平面内的任一向量，(这是变化的)都可以唯一地由这两个向量(基底)线性表示，(这是不变的)．其五，分类讨论思想方法：就探索平面向量基本定理的过程而言，针对“不同位置”的向量的分解，例如零向量与非零向量、与基底共线向量等，其中蕴含着分类讨论的思想方法．

3.1.3素养主线

从学生学习角度，就平面向量基本定理的建构过程，主要体现出以下几种关键能力：数学建模、直观想象、逻辑推理．关键能力是核心素养的重要成分．进而可以认为，教学中应该注重提高这几种关键能力，事实上也就是在发展学生的核心素养[3]．

(1)数学建模

平面向量基本定理可以认为是建立了平面向量表示的一种模型．将任一向量在两个方向(基底)上进行分解，依据的是平行四边形法则，这可谓是“用数学方法解决问题”．将这一过程理解为“数学建模”有积极意义：按李尚志教授观点，“……用现成公式加以变通解决不现成的问题，就是数学核心素养中的‘数学建模’”；[5]在认定其为“数学建模”基础上的教学，就要主动突出数学建模的过程，这对深化数学应用，培养创新意识，提高实践能力，进而发展其数学建模核心素养，将起到重要的积极的作用．

(2)直观想象

在建立平面向量基本定理的过程中，尤其是任一向量在两个方向(基底)上的分解，是通过几何图形、利用平行四边形法则进行的．其中有对“任一向量”的分类探究，得到统一的结论．这正是“借助几何直观……利用……图形……建立形与数的关系，构建数学问题的直观模型．”[4]所以，在本课过程中，充分利用几何图形，描述问题、直观理解、探索关系，是发展直观想象核心素养所需要的．

(3)逻辑推理

主要表现为两部分．一方面是通过分类讨论，就各种可能的情形进行推理：平面内任一向量都可以在两个方向(基底)上分解；这种分解的结果是唯一的．这个过程实质上是逻辑推理，但限于条件，不能给出严格的演绎推理证明．例如，除了依平行四边形法则分解，是否还有另外不同的分解途径，这些途径与此分解的结果是否相同，都不易给出严格证明．所以，从学生认知心理角度，这里的推理认定为合情推理似乎更恰当些．

另一方面，完成任一向量在两个方向(基底)上的分解后，利用向量共线定理证明这一有序实数对“存在且唯一”，则属于演绎推理了．这也是建立平面向量基本定理的基础．与此同时，也体现出了向量共线定理是平面向量基本定理的特例，即有序实数对中有一个数为0；平面向量基本定理是向量共线定理的推广——一维到二维．

逻辑推理主要表现为：“……发现问题和提出问题，探索和表述论证过程……”[4]所以，在平面向量基本定理探索过程的教学中，要创设恰当情境，启发引导学生主动提出问题，利用图形探索，依据已有的向量共线定理进行推理，并尝试概括平面向量基本定理，达到较为充分的心理认可……为发展学生核心素养，做出可能的努力．

3.2 基于三条主线的课时教学设计(片断)

如前所述，教学应该突出三条主线，三条主线的关系是：突出知识主线，看重方法暗线，看见素养眼线．发展核心素是根本目标，但核心素养综合地体现在发现和提出问题、分析与解决问题的过程中．从本课内容中所析取出的三个核心素养，其“主要表现”为：数学建模“在实际情境中从数学的视角提出问题……”；逻辑推理“……发现问题和提出问题”．[3]发现和提出问题，就要基于情境，提出数学问题；分析与解决问题，就是要分析与解决所提出的问题．所以基于这三条主线的教学设计，仍然要以解决问题为导向，以知识发生发展的逻辑过程为基本线索，为学生构建前后一致、逻辑连贯的探究学习过程．[6]在知识的教学中渗透数学思想方法，进而为发展学生的核心素养作出可能的贡献．其中，启发引导学生主动提出问题，可能是本课的重中之重．[7]

这里，就“情境与问题”，[3]具体到本课即创设情境，提出本课题给出如下选择与思考．

(1)从共线向量定理引入

两个向量有何关系？——共线与不共线，共线时有向量共线定理；研究了共线，也就同时研究了不共线.

平面内三个向量有何关系？若其中存在两个向量共线的情形，则问题可转化为两个向量是否共线的问题，这是已经解决了的问题；若不存在任两个向量共线的情形，那么它们将有何关系？——将它们平移到同一个起点，画出图形，结合平行四边形法则……尝试提出问题……

(2)从探求向量代数表示引入

向量兼有数与形的特征，用有向线段表示向量，用平行四边形法则进行向量加法、减法运算，一定意义下属于几何范畴．基于此背景提出问题：

——你能提出什么问题？

——是否可能存在向量的代数形式？进而研究代数形式下向量的运算？

这样就明确了学习的任务，探究的方向．至于怎样研究，就要回到已有的认知基础，即回到几何情境上去．或者说，教师要给出情境，提出具体任务：既然两个向量可以合成一个向量，那么探索一个向量在两个向量方向上的分解可能是有意义的……比如知道两个向量中的一个，以及它们的合向量，可否求作另一个……

另一种思路值得探讨：从平面直角坐标系到有序实数对，这虽与教材安排顺序及坐标的由来相悖，但也许有合理之处：从熟悉到陌生，从特殊到一般，并且重点突出了坐标的本质——有序实数对．设想如下：

——用代数去表示向量，还要兼有几何特征，你觉得在什么情境下探讨较方便？

启发学生萌发到平面直角坐标系中去研究的念头，并基于平面直角坐标系，从探寻特殊的基向量(事实上是标准正交基)出发，通过任一向量都可以用标准正交基线性表示，构建三个向量之间的关系，通过运算推理，得到一个向量用另外两个向量线性表示的结论，此时 “离开”平面直角坐标系背景，得到定理．笔者认为，可以视学情允许，尝试这种思路，并进一步与常规思路对比分析．

(3)从物理背景中引入

借助于“力的平衡”情境，观察力的合成与分解，类比向量与力的共同特征，提出类似的问题：向量在两个方向(基底)上的分解．这可能是比较自然合理的，而且是基于“科学情境”提出问题．这对于发展学生核心素养是有益的：引导学生善于观察，在“关联的情境”中提出数学问题，主动发现研究的方法，类比迁移到所研究的新问题上去，并借助已有知识(平行四边形法则)去解决所提出的新问题……

(4)从平行四边形法则引入

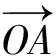
图3 向量的合成与分解