关注探究拓展过程 发展数学核心素养①——以一道中考几何模拟试题的解答与拓展过程为例

白雪峰 郭文征

(1.北京第17中学 100124；2.北京市芳草地国际学校富力分校 100121)

《普通高中数学课程标准(2017年版)》(以下简称“标准”)明确指出：数学在形成人的理性思维精神、科学精神和促进个人智力发展的过程中发挥着不可替代的作用．数学教学要以发展学生数学学科核心素养为导向，深刻把握数学内容的本质，引导学生会用数学的思维思考世界．[1]正如G·波利亚指出：思维应该在学生的头脑中产生出来，而教师仅仅应起一个产婆的作用．因此，教师要善于通过精准选择学习材料，系统设计探究任务，合理组织学习活动，激发学生学习兴趣，指导学生体验发现，激活学生数学思维，发展学生的数学核心素养．

在探究过程中，学生围绕某个数学问题展开研究学习，通过主动思考将逐步理解直观与严谨的关系，体验发现与创造的乐趣，学生敢于拓展与探究的思维品质、勇于批判与质疑的理性精神都将得到不同程度的深化与发展．下面，笔者仅以2018年北京市平谷区中考数学第一次模拟试卷第27题为例，阐述这方面的研究与实践．

问题在△ABC中，AB=AC，CD⊥BC于点C，交∠ABC的平分线于点D，AE平分∠BAC交BD于点E，过点E作EF∥BC交AC于点F，连接DF．

(1)补全图1；

(2)如图1，当∠BAC=90°时，

①求证：BE=DE；

②写出判断DF与AB的位置关系的思路(不用写出证明过程)；

(3)如图2，当∠BAC=α时，直接写出α，DF，AE的关系．

图1

图2

本题是一道拓展探究空间广阔、数学育人功能丰富、充分体现素养立意的几何试题．命题者以特殊三角形为背景，从研究等腰三角形和直角三角形的性质为切入点，步步推进，层层深入，将问题不断拓展到一般的等腰三角形，同时，基于三角形相关的基础知识和基本技能的考查，突出考查了学生的合情推理、演绎推理能力和创新思维品质．为了能够全面反映和深度理解命题者的命题意图，笔者首先给出上述问题每一问的严格证明．

1 原模拟试题及其全面解答

(1)补全图1，如图3，过点E作EF∥BC交AC于点F，连接DF．

图3

(2)如图3，①证明，延长AE与BC交于点H．

因为AB=AC，∠BAC=90°，

所以△ABC为等腰直角三角形．

又AE为顶角∠BAC的平分线，

所以AH⊥BC，且H为BC的中点．

注意到DC⊥BC，所以AH∥DC．

所以E为BD的中点．即BE=DE．

②判断DF∥AB．

说明该模拟试题是把等腰直角△ABC中的几何性质拓展到一般的等腰三角形，笔者希望把上述问题中的等腰三角形的性质拓展到一般直角三角形．更进一步地，再把其中等腰直角三角形的性质拓展到一般的三角形．因此，笔者将给出问题(2)中②的多种证明，为探究拓展铺垫证明思路．

图3(a)

证法1如图3(a)，延长DF与BC交于点G．

因为△ABC为等腰直角三角形，

所以∠ACB=45°．

因为DC⊥BC，

所以∠DCF=45°．

在△DBG中，

因为E为BD中点，EF∥BG，

所以F为DG的中点．

所以CF为直角△DCG斜边DG的中线．

所以FC=FD．

所以∠CDF=45°．

所以∠DFC=90°．

注意到∠BAC=90°，所以DF∥AB．

证法2如图3(b)，过点D作DK垂直BA的延长线于点K，则有DC=DK，DK∥AF．设BD与AC交于点G，易证∠ABG=∠CBG，∠1=∠2=∠3=∠4=∠CDG．

图3(b)

所以AE=AG，CD=CG．

过点G作GP⊥BC于点P，

则有GP=GA=AE．

易证△AEF≌△GPC，

即两个等腰直角三角形全等．

所以AF=CG，所以AF=DK．

所以四边形AFDK为矩形．

所以DF⊥AC．

又BA⊥AC，所以DF∥AB．

证法3如图3(c)，延长CD与BA的延长线交于点G．

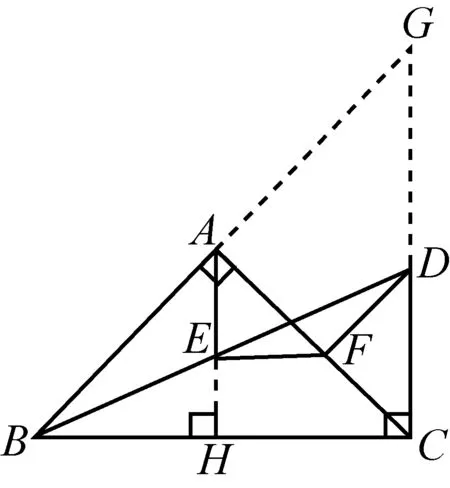
图3(c)

因为EF∥HC，

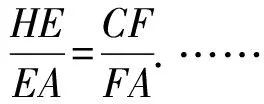
因为AH⊥BC，GC⊥BC，

所以AH∥CG．

所以DF∥GA，即DF∥AB．

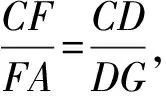
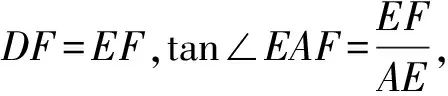
证明如图4，延长AE与BC交于点H，则有∠1=∠2，AH⊥BC．

图4

因为DC⊥BC，所以AH∥DC．

所以∠3=∠2=∠1．

延长DF与BC交于点G,

因为E为BD中点，

又EF∥BG，

所以F为DG的中点．

所以CF为Rt△DCG的斜边DG的中线，

所以FC=FD,所以∠3=∠4,所以∠1=∠4．

所以∠ABC=∠DGC．

所以AB∥DG，即DF∥AB．

所以∠6=∠8．

因为EF∥BC，所以∠7=∠5．

因为BD为∠ABC平分线，所以∠5=∠6．

所以∠7=∠8．所以DF=EF．

因为EF∥BC，所以∠AEF=∠AHC=90°．

说明在图4中，AE为∠BAC的平分线，BE为∠ABC的平分线，所以E为△BAC的内心．FC=FD，又FD=FE，所以FC=FD=FE，即点F为以D、C、E为顶点的三角形的外心．从“内心”“外心”切入，我们可以拓展第(3)问，即把原问题中等腰直角三角形的背景拓展演变为以一般三角形为背景的一个新问题．

2 问题拓展与解析

基于上述问题证明和拓展的思路，笔者把原中考题拓展到一般的直角三角形，进而再拓展到一般的三角形．

拓展问题1如图5，在△ABC中，BA⊥CA，AH⊥BC于点H，DC⊥BC于点C，交∠ABC的平分线于点D，BD交AH于点E，过点E作EF∥BC交AC于点F，连接DF．

求证：DF∥AB，DF=EF．

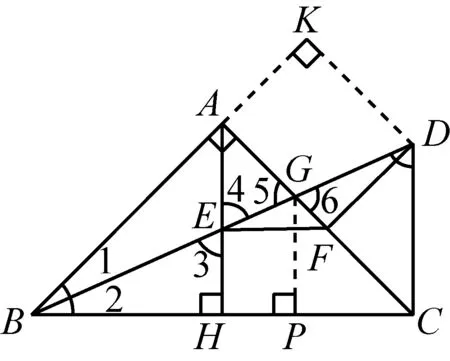
图5

证明如图5，过点D作DK垂直于BA的延长线于点K，则有DK∥FA，DC=DK．设BD与AC交于点G，易证∠1=∠2，∠3=∠4=∠5=∠6=∠CDG．所以AE=AG，CG=CD．

过点G作GP⊥BC于点P，

则有AG=GP=AE．

因为EF∥BC，

所以∠AEF=∠AHC=90°，

∠AFE=∠GCP．

所以Rt△AEF≌Rt△GPC．

所以AF=CG=DC=DK．

所以四边形AFDK为矩形．所以DF⊥AC．

又BA⊥AC，所以DF∥AB，∠1=∠EDF．

因为EF∥BC，所以∠2=∠DEF．

所以∠EDF=∠DEF．所以EF=DF．

说明如图5(a)，在Rt△ABC中，∠BAC=90°，AH⊥BC于点H，∠ABC的平分线交AH于点E，交AC于点G，则有AE=AG．本问题是中考数学及几何习题集上常见的问题．如图5(b)，在Rt△ABC中，∠BAC=90°，AH⊥BC于点H，∠ABC的平分线交AH于点E，交AC于点G．EF∥BC交AC于点F，则有AF=GC．这个问题是上面问题的引申题，拓展问题1也可以看成是上面问题的拓展．

图5(a)

图5(b)

图6

拓展问题2已知：如图6，E为△ABC的内心，EF∥BC交AC于点F，CD∥AE交BE的延长线于点D．求证：F为△DCE的外心．

证明如图6，延长AE交BC于点H，延长CD交BA的延长线于点G，连接DF．因为EF∥BC，

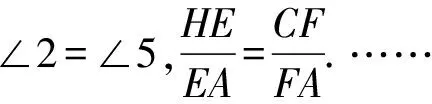
因为CD∥AE，

所以∠1=∠6．

因为E为△ABC的内心，

所以∠1=∠2，∠3=∠4．

所以∠5=∠6．所以EF=DF．

因为DF∥AB，DC∥AE且方向相同，

所以∠3=∠8．所以∠4=∠8．所以∠7=∠8．

所以CF=DF．所以EF=DF=CF．

所以F为△DCE的外心．

说明证明拓展问题2的最终目标就是要证明EF、DF、CF三条线段相等．回顾上述证明过程，笔者基于已知条件中的平行条件，通过两次利用平行线截线段成比例定理，再证得一组平行线，即DF∥AB，最后通过点E为△ABC的内心和三组平行线等条件证得∠5与∠6、∠7与∠8两组角分别相等，从而获得两个等腰三角形△EFD和△CFD，使问题得证．

3 深度反思与启示

前苏联著名教育实践家和教育理论家苏霍姆林斯基告诉教师：“在人的心灵深处，都有一种根深蒂固的需要，这就是希望感到自己是一个发现者、研究者、探索者．在儿童的精神世界中，这种需要特别强烈．”[2]笔者认为，中学生正处在思维发展、能力提升和品格塑造的黄金时期，有意义的数学学习活动正是促进学生思维品质和学习能力提升的重要平台．因此，更需要教师引导和指导学生在接受和记忆、模仿和练习的基础上，大胆地开展思考与发现、探究与创新的学习活动，在系统建构知识体系的基础上，形成深入思考的习惯、探究的方法和创造的信心，不断深化对数学思想与价值观点的理解．

3.1 让独立思考成为学生数学学习的新常态

学生的数学学习活动应该是生动活泼、个性鲜活的有意义的过程，学习方式也一定是丰富多彩的，认真听讲、积极思考、动手实践、主动探索、合作探究、表达交流、展示分享等等．[3]在课堂教学中，教师要基于内容、学情等主客观条件，善于选择恰当的学习方式，其中独立思考不应被冷落．

独立思考是一个人内心成长的重要过程，是学生形成客观判断能力、质疑思维品质和勇于探究能力的有效途径．因此，教师要善于设计学习情境、活动任务和思考问题，激发学生乐于思考的内在动力和潜能；在提出思考问题、布置活动任务后，要学会停顿和耐心等待，为学生创设独立思考问题、深度理解问题、形成表达意见、展开研讨交流和修正完善结论等思维活动的时空．同时，通过仔细观察学生的面部表情和活动状态，科学分析并准确研判学生的学习心理状态，恰时、恰点、恰当的启发和追问，或者及时调整和改进教学走向．在学生回答时，要善于引导全班学生认真倾听，深入思考同伴的回答情况，运用延迟评价理论，引导学生自评或互评，以提高学生思考的深度和广度．长此以往，独立思考必将成为学生开展数学学习的新常态．

当独立、深刻且规范化的思考变成了学生的数学学习习惯，当学会有逻辑且创造性的思考问题成为教师课堂教学的重要目标，当思想交锋、智慧碰撞、师生共同学习和探讨交流成为数学课堂的必然样态，数学育人目标的实现也将成为可能．

3.2 让拓展探究成为学生数学发现的源动力

“标准”倡导教师要转变数学教学方式，在实践中推动探究式教学，重视学生自主参与及其探究能力的培养，发展学生的数学核心素养．平面几何问题的推理证明是培养学生创造性思维品质、发展学生逻辑推理素养和理性思维精神的有效载体，平面几何问题的研究过程也是促进学生深入参与学习、培养学生探究能力的重要途径，中学数学教师应该十分重视并充分发挥平面几何教学的教育价值．

例如，在解决平面几何问题时常常需要添加辅助线，恰当准确地添加辅助线不仅可以使问题迎刃而解，还可以使问题的解决过程简化，论证表述简洁．但是，在课堂教学中，学生对添加辅助线常常感到困惑无助，不明所以．学生不明白为何要添加辅助线，更不理解每一种添加辅助线的方法到底是如何想到的，学生常常自责都是因为自己脑子不好使，想不到要这样或那样添加辅助线．时间久了，学生便失去了学习平面几何的自信心，遇到几何问题或难题只想躲着走，更别谈体验思考的乐趣和成功的喜悦了．要想改变这样的学习效果，就需要教师精心选择几何问题，精致设计探究活动，引导学生理解添加辅助线的目的，即通过合理添加辅助线将内隐在问题中的几何图形的特征和性质外显出来，将题设条件和结论之间建立起逻辑关系，进而创造利用定义、定理等解决几何问题的条件，达到推证结论的目的．同时，教师要重视几何直观对提高学生探究能力的重要作用，指导学生学会基于对几何图形特征的深入观察分析展开想象，引导学生借助几何图形直觉地发现和描述问题，形成大胆的设想、联想或猜想，以此为线索提出解决问题的方案，探索推理论证的过程，有逻辑地进行表达和交流，进而经过精细地逻辑加工得出问题的完整解答．

教师要努力让拓展探究成为学生数学发现的动力之源，切实引导学生不断追问添加辅助线的思路是如何想到的，耐心指导学生回顾反思不同添加辅助线的思路对证明过程的影响，通过类比学习和对比研究驱动学生积极思考和主动探究，通过经历探求简洁思路和简明的方法过程，掌握添加辅助线的一般思路和基本规律，体会蕴涵于几何问题解决过程中的思维深刻之美、逻辑严谨之美和表达简洁之美．

3.3 让数学表达成为学生素养发展的助推器

数学教育承载着落实立德树人的根本任务，提升学生的数学核心素养，引导学生学会运用数学的语言表达世界是重要的育人目标之一．在中学数学课堂教学中，教师要充分发挥学生的学习主体作用，努力成为学生开展有效学习的设计者、组织者、引导者与合作者．在学生学习的重难点、思维障碍点等关键之处，教师要敢于慢下来，甚至是停下来，让学生获得足够的时间和空间，充分体验观察、实践、猜想、计算、推理和验证的学习活动过程，进一步拓宽学生思考、表达和交流的途径和方式，指导学生把没想明白、理解不清、说不出来的困惑和问题大胆地表达出来，教师也要学会耐心倾听学生学习过程中心里话、悄悄话，通过指导学生输出促进他们的输入，开启学生思维和讨论的大门，促进师生、生生之间高质量的思维上的互动．当学习的课堂变成了一个和谐温馨的对话场所，课堂的学习也就会变得灵活生动起来，师生将会获得更多意外的精彩，共同体验到学习知识、探讨问题、获得发现的快乐．

众所周知，数学是关于思维的科学，数学独特的育人功能主要在培养学生的思维，特别是逻辑思维，要使学生学会思考，特别是学会有逻辑的思考、创造性的思考．平面几何在培养学生思维能力方面具有不可替代的作用．[4]

在平面几何教学中，教师要善于利用那些“有意义且不复杂”的题目启发学生，示以思维之道．通过引导学生深入挖掘几何图形的重要特征，帮助学生借助图形把握几何问题的数学本质，指导学生通过“一题多证(解)、一题多问、一题多变”等变式教学方式深入地开展思考和探究拓展，形成研究平面几何问题的基本套路和思维体系，培养他们重论据、有条理、合乎逻辑的思维品质和理性精神，将数学之大道自然融入问题的发现、提出、分析与解决问题的全过程之中，切实发挥平面几何教学的教育价值.