2019年东京大学入学考试理科数学题目与解析
2020-04-28董心君
董心君
(东南大学交通学院 211189)
1 试题与解析
东京大学的自主招生考试起源于1961年,除了1969年年初由于“とうだいふんそう” (东京大学纷争)事件取消,至今已经是第58年.考试分为文理科,理科时间两个半小时,一共六道题,考试范围涉及不定积分、函数、立体几何、复数平面、线性代数等内容.本文翻译并解析了2019年的理科数学试题.
1.求定积分



解:如图1,设AQ长x,DR长y,


图1
S△DPR+S四边形BCRP
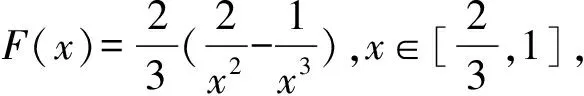

3.空间坐标内有5点A(2,0,0),B(0,2,0),C(-2,0,0),D(0,-2,0),E(0,0,-2),将过线段AB中点M、线段AD中点N,且与直线AE平行的平面设为α.设点P(p,0,2),其中2 (1)在同一平面上画出八面体PABCDE被y=0所截图形与α被y=0所截图形. (2)求出八面体PABCDE被α所截切面为八边形时p的范围. (3)若实数p在第(2)问的所求范围内,在由八面体PABCDE被α所截的平面内,点(x,y,z)在y≥0、z≥0的范围内移动,求坐标系内的点(y,z)的移动范围的面积. 得-2a-2c=0, 令a=1,得α:x-z-1=0, 其被y=0所截部分即为直线z=x-1. 八面体PABCDE可分为四棱锥P-ABCD与四棱锥E-ABCD,点P、E、A、C都在平面y=0上,因此八面体PABCDE被y=0所截部分为四边形AECP. 如图2,当2 图2 (2)不妨先讨论八面体PABCDE的 12条棱与α的交点个数. 当2 当p=3时,棱边PA、PB、PC、PD与α交于P点,不合题意. 当3 综上,当3 (3)求y≥0、z≥0的部分,考虑平面α与四面体P-ABC的截面即可, 由对称性可知,线段PD与α交点坐标 图3 4.n为大于1的整数 (1)求n2+1与5n2+9的最大公约数dn. (2)证明(n2+1)(5n2+9)不是整数的平方. 解:(1)n=1时,d1=2;n=2时,d2=1. 若n为偶数,显然n2+1与4互质,dn为1. 若n为奇数,不妨设n=2k+1,k≥1, n2+1=2(2k2+2k+1),2k2+2k+1为奇数, 此时n2+1与4的最大公约数为2. (2)先证明一个命题:给定两个互质的正整数(均大于1),则它们的乘积为完全平方数的充要条件是这两个数都是完全平方数.证明如下: 必要性:由于两个数互质,它们必定没有相同的质因子.考虑完全平方数的质因子分解,则其每个质因子必定都是偶数次幂,且把它们分配到互质的两个数后,每个数的质因子都必定还是偶数次幂,即两个数都是完全平方数. 充分性:显然. n为偶数时,dn=1,n2+1显然不是完全平方数,因此(n2+1)(5n2+9)不为完全平方数. n为奇数时,不妨设n=2k+1,k≥1,(n2+1)·(5n2+9)=4(2k2+2k+1)(10k2+10k+7),dn=2,即证明(2k2+2k+1)(10k2+10k+7)为完全平方数,则必须2k2+2k+1、10k2+10k+7均为完全平方数,而10k2+10k+7的个位数恒为7,必不为完全平方数,即(n2+1)(5n2+9)不为完全平方数. 综上,命题得证. 5.回答以下问题 (1)n为大于1的整数.证明关于x的方程x2n-1=cosx有唯一实数解an. (2)对于第(1)问的实数解an,证明cosan>cos1. (3)对于第(1)问的给定数列{an},求 (1)证明:-1≤cosx≤1,若存在实数解an,an∈(-1,1). 令F(x)=x2n-1-cosx,F(0)=-1,F(1)=1-cos1>0,F(-1)=-1-cos1<0. 0 在(-1,0)内,0 综上,命题得证. (2)余弦函数在(0,1)递减,第(1)问已知0 两边取极限,故 6.复数α,β,γ,δ与实数a,b满足下面3个条件, 条件1:α,β,γ,δ互异; 条件2:α,β,γ,δ为4次方程z4-2z3-2az+b=0的解; 条件3:αβ+γδ为纯虚数. (1)若α,β,γ,δ中恰好有2个实数,证明剩下的2个复数共轭; (2)用a表示b; (3)将α+β的范围在复平面上表示出来. 解:(1)由条件2得方程: (z-α)(z-β)(z-γ)(z-δ)=0, 展开后和原方程对比系数: α+β+γ+δ=2,αβγδ=b, αβγ+αγδ+αβδ+βγδ=2a, 不妨设α∈R、β∈R,则γ+δ∈R,γδ∈R,由韦达定理逆定理可知:γ、δ必为某一元二次方程的两根,由一元二次方程求根公式可知γ与δ必为共轭复数. (2)由条件3可知,方程必有复数解,故原方程有1或 2对共轭复数解,下分类讨论: 1)若方程有2对共轭复数解,不妨设方程4个解为m+ni,m-ni,1-m-ti,1-m+ti,其中m、n、t∈R. (m+ni)(1-m+ti)+(m-ni)(1-m-ti) =2m(1-m)-2nt∈R, (m+ni)(m-ni)+(1+ti)(1-ti) =1+m2+n2+t2∈R, 与条件3矛盾,不成立. 2)故方程有一对实数解,一对虚数解,设4个解为m,n,s-ti,s+ti,其中m、n、s、t∈R. 条件3成立,仅有m(s+ti)+n(s-ti)=(m+n)s+(m-n)ti为纯虚数, 故m=-n,四个解为±n、1-ti,1+ti.n、t均为不为0的实数. 故有(z-n)(z+n)(z-1+ti)(z-1-ti)=0,展开后与原方程对比系数,有: 消去参数,得b=-a2. (3)不妨令α=n、β=1-ti,α+β=1+n-ti, 图4 通过前文对2019年东京大学入学考试理科试题的介绍,可以发现东京大学的数学招生题有如下特点: (1)难度由浅入深,第一道积分题与国内研究生入学考试数学科目简答题难度相当,第二道平面几何、第三道题立体几何相当于国内部分地区高考中档题,后三道题难度较大,与国内知名大学自主招生压轴题相当. (2)知识内容考查范围大、数量多.第一题积分考察了学生的分部积分能力以及对常用积分公式的计算;第二题本质考察的是函数求极值问题;第三题与国内主流的立体几何考察内容不同,考察的是学生的三维图形想象能力;第四题涉及最大公约数,本质上考察的是质因数分解;第五题涉及数列、极限,其中第一问的放缩、第三问的求极限部分难度较大;压轴题是关于一元高次方程的解,解题所涉及的“棣莫弗定理”、“虚根成对定理”,是高中数字竞赛的教学内容. (3)题目数量少,步骤多,更注重考察学生的探究能力以及综合解题能力,每个题目各小问层次分明,难度递增,考察内容丰富.事实上,复试阶段的数学试题更能体现这一点,学生要在2个半小时的时间内解决三道题,极大考察了学生的阅读与研究能力. 由于中日两国教育资源、教学理念、高考制度不尽相同,我们不能对日本的招生题目进行完全照搬学习,但显然日本考卷在题型设置、考察内容等方面,是值得借鉴并学习的.适逢中国高考制度改革,国内知名大学的自主招生政策也陆续出炉,希望各方能通过借鉴国外的试卷的长处,改进现有的数学考卷,能更合理、有效地选拔人才.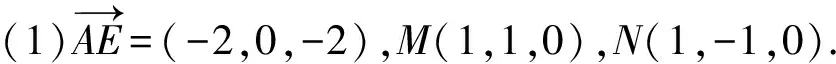
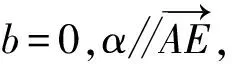

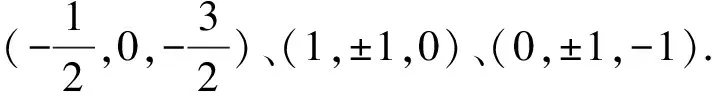










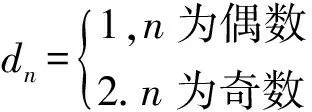


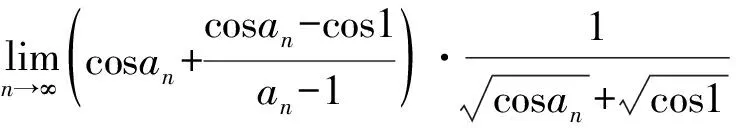


2 总结与反思
