基于加权K近邻的特征选择方法

李双杰，张开翔，王士栋，王淑琴

（天津师范大学 计算机与信息工程学院，天津 300387）

在当今大数据时代，很多应用中数据集的维度很高，尤其在DNA 微序列分析、图像处理、模式识别和文本分类等领域，数据具有极高的维度[1-3]，然而，在分类任务中，过高维度造成的“维度诅咒”现象会导致过拟合，从而降低学习模型的泛化能力[4]，而且许多特征都是不相关或者冗余特征，它们在分类学习过程中毫无用处.特征选择是机器学习的一个重要的数据预处理过程[5-6]， 其目标就是剔除不相关和冗余特征，以减少学习维度，并在可接受的时间内获得高准确率，同时降低训练模型所用的时间和存储空间[7].

在过去几年里，各种各样的特征选择算法被相继提出[8].根据分类器是否独立，特征选择方法可以分为Filter、Wrapper 和 Embedded 3 类.由于在选择候选特征子集时，Filter 方法与分类器相分离[9-11]，因此Filter方法相对简单，时间复杂度较低，可以和多种分类器结合.Wrapper 方法通常以分类器的性能作为候选特征子集的评价准则[12]， 因此它具有较好的分类性能，但其计算开销通常比Filter 方法大很多.Embedded 方法结合了Filter 方法和Wrapper 方法的优点，在学习算法训练过程中可以自动进行特征选择[13]，因此它通常优于Filter 方法和Wrapper 方法.

在模式识别中，K 近邻算法经常用于分类和回归任务[14-15].K 近邻的优势是算法简单且对异常值不敏感.近年来，它也被用于特征选择方法的研究.文献[16]提出了一种基于KNN 的加权策略（MKNN）方法，它使用传统的信息增益作为特征选择方法，MKNN 作为分析基因表达数据的分类器，该方法根据数据集中每一类别中样本到该类中心点的距离对样本进行加权，从而使K 个近邻样本对判定测试样本类别的贡献不同，但该方法在计算距离时没有考虑特征的重要性.文献[17]将KNN 作为一个基本单元集成到特征选择框架中，用以评价候选特征子集的优劣，该方法通过随机选择多个特征子集，用KNN 评价特征子集的分类准确率，最后将相应准确率的平均值作为特征的支持度，支持度越高表示特征与类别的相关性越大， 该方法将KNN 视为一个黑盒子， 没有对KNN 算法展开研究.在对测试样本的类别进行判定时，一方面，应依据其K 个近邻样本与其距离的大小不同来决定每个近邻样本对类别的贡献，距离越小的贡献也应越大；另一方面，由于每个特征对样本类别的重要程度是不同的，所以在计算样本间距离时，还应考虑每个特征的重要程度.为此，本文提出了一种基于加权K 近邻的特征选择算法，该算法在计算样本类别时既考虑每个特征的重要程度，又考虑近邻样本的距离，并使用遗传算法搜索最优特征权重向量，最后按最优特征权重向量对所有特征降序排序，依次选出对应的前N 个特征组成特征子集，并用分类器评价其质量，本文方法属于Filter 方法.使用6 个真实数据集，将本文方法与现有的 3 种特征选择方法 MIFS[18]、DISR[19]和 CIFE[20]进行比较， 并使用 K 近邻（KNN）、随机森林（random forest）、朴素贝叶斯（NB）、决策树（decision tree）和支持向量机（SVM）5 种分类器对每个方法所选择的特征进行分类预测，实验结果表明本文方法具有较好的分类性能.

1 基于加权K近邻的特征选择方法

本文提出的基于加权K 近邻的特征选择方法，简记为 WKNNFS（feature selection based on weighted K-nearest neighbors）.首先初始化一个种群，种群中每个个体代表一个特征权重向量；然后用加权K 近邻预测样本类别，并设计合适的适应度函数；最后用遗传算法搜索最优特征权重向量.

1.1 相关定义

对于分类任务，测试样本的类别由K 个近邻投票决定，将测试样本归为票数最多的类别.对于回归任务，测试样本的类别由K 个近邻的目标值的算术平均值决定.以下若无特殊说明均为处理回归任务.给定一个回归问题 D=（F，X，Y）， F={f1， f2，…， fm}为特征集合， X={x1，x2，…，xn}为包含 n 个样本的数据集，xi=（xi1，xi2，…，xim）（1≤i≤n）为样本 xi的观测值， Y={y1，y2，…，yn}为目标变量集合，则测试样本 xi的预测值Pi为

其中：K 为KNN 中选择的近邻个数；yj为K 个近邻样本的目标变量.

定义一个特征权重向量 wf=（wf1，wf2，…，wfm）， 则对特征加权后的样本观测值用Hadamard 积表示为

使用特征加权后样本xi与xj的欧几里得距离为

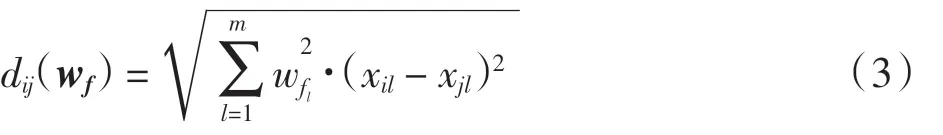
传统的K 近邻方法中，训练集中用于预测测试样本类别的K 个近邻样本的贡献是相同的，这忽略了不同近邻样本的重要性的大小，距离越小，它们属于同一类别的可能性越大，也就越重要.因此，可以对K个近邻的贡献进行加权，距离越小的近邻分配的权重越大.距离加权函数w 应满足以下性质：

（1）w（d）为一个单调递减函数.

（2） w（0） =1.

（3）w（∞）=0.

本文采用的距离加权函数为

考虑特征加权与距离加权后测试样本xi的预测值Pi（wf）定义为

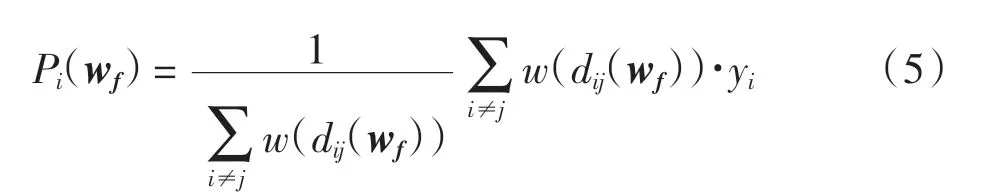
损失函数用预测值Pi（wf）与目标函数的真实值yi的差表示，定义损失函数为

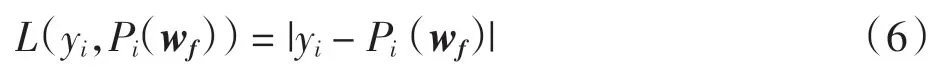
成本函数用所有训练样本损失函数的平均值表示，成本函数值越小说明整体的预测误差越小.成本函数定义为

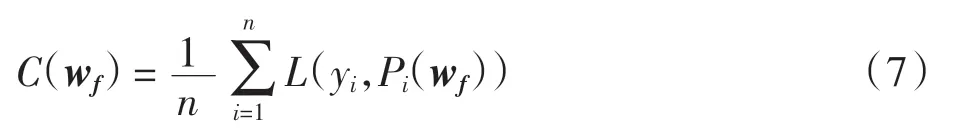
1.2 遗传算法

采用遗传算法搜索最优特征权重向量.

（1）初始化种群：使用（0，1）中的实数随机初始化含有m 位基因的个体，每个个体代表一个特征权重向量.

（2）适应度函数：个体t 的适应度函数定义为

其中Max 是给定的使Ft（wf）≥0 的正整数.

（3）选择算子： 使用轮盘赌选择（也称为比例选择方法）[21]作为选择算子.

（4）交叉算子： 因为本文使用的是实数编码方式，因此采用算术交叉算子，使下一代尽可能地遗传上一代中优秀个体的性状.先根据概率随机选择一对父代个体P1、P2作为双亲，然后进行如下随机线性组合产生 2 个新的子代个体

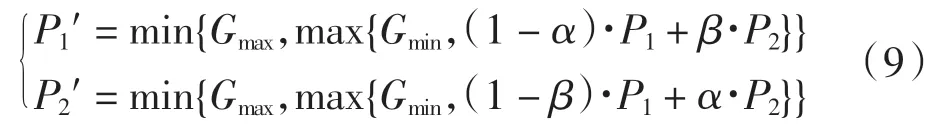
其中：α、β 为（0，1）中的随机数，个体基因的取值范围为[Gmin， Gmax].如果（1 - α）·P1+ β·P2的值小于 Gmin（或大于Gmax）， 则P1′的值为Gmin（或Gmax）， P2′的值同理可得.

（5）变异算子：变异算子采用高斯变异，这种操作方式能重点搜索原个体附近的某个局部区域.高斯变异使用符合均值为μ、方差为σ2的正态分布的一个随机数Q 来替换原来的基因值.Q 的计算公式为

其中： ri是在[0，1]范围内均匀分布的随机数， μ 和 σ的计算公式为

1.3 WKNNFS特征选择方法

对于回归问题D=（F，X，Y），首先，用实数编码方式初始化一个种群， 种群中每个个体为一个权重向量；然后，对于当前代的每个个体t，用基于K 近邻的方法计算训练集中每个样本的预测值Pi（wf）及该个体对应的适应度函数值Ft（wf），为了更好地找到全局最优解，将当前代最大的适应度函数值和对应个体保存到Results 中；最后，分别执行选择、交叉、变异3 个遗传算子产生新的种群，并重复上述操作直到满足终止条件，即达到给定的迭代次数.

迭代操作结束后，将Results 中的适应度函数值降序排序，获得适应度值最高的个体，则可得到最优特征权重向量，再对最优特征权重降序排序，即可得到对应特征分类能力的降序序列.

WKNNFS 特征选择方法的具体流程如下：

2 实验与性能分析

2.1 数据集

为验证WKNNFS 算法的正确性和有效性， 在6个数据集 Q_green、hcc-data2、Sonar、clean1、Prostate 和brain 上进行实验，前4 个数据集下载自UCI 机器学习库[22]，后2 个数据集下载自学习网站http：//ligarto.org/.实验中对这些数据均做了归一化处理，所用数据集的具体描述见表1.

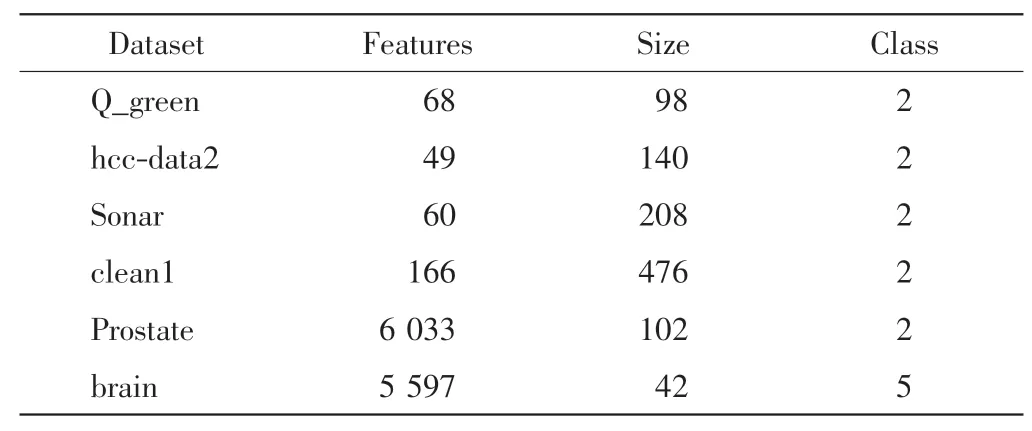
表1 数据集Tab.1 Datasets

2.2 实验环境及参数设置

使用PyCharm 集成开发环境，对每个数据集进行十重交叉检验.在以上6 个数据集上，将WKNNFS 与现有的3 种特征选择方法MIFS、DISR 和CIFE 进行比较，并使用K 近邻、随机森林、朴素贝叶斯、决策树和支持向量机5 种分类器对每个方法所选择的特征进行分类预测.实验中初始化种群包含80 个个体，迭代次数为260 次，交叉概率为0.8，变异概率为0.08.

2.3 实验结果及性能分析

实验所用数据集中部分是不平衡数据集，所以本文采用F1-measuer 指标来衡量分类性能.F1-measure指标综合了精确度（precision）和召回率（recall），其定义为实验结果见图1，图中，横坐标表示选取前N 个特征，纵坐标为选取前N 个特征后5 个分类器进行分类预测得到的F1 的平均值.

由图1 可见，WKNNFS 与其他3 种方法相比，不仅获得的分类性能最高， 而且在多数情况下最快获得了最高分类性能.在数据集Q_green、hcc-data2 和Sonar 上（图1（a）～（c））， WKNNFS 相比另外 3 种方法能够很快达到最高分类性能.在数据集clean1 上（图1（d））， 当选取前 N（N=1，2，…，20）个特征时， 4 种方法的分类性能相近，但随着特征数的增加，WKNNFS的性能明显优于另外3 种方法.在数据集Prostate 和brain 上（图1（e）～（f））， WKNNFS 达到最高分类性能的过程较慢， 这可能是因为这2 个数据集的维度较高.由图1（a）和（b）可见， 4 种方法的分类性能达到最高后， 再增加所选特征数， 分类性能反而呈下降趋势，这表明特征数过高可能会降低模型的分类性能.

表2 给出了在6 个数据集上4 种方法获得的最高分类性能（F1）及其对应的特征数（m）.每个数据集上的最高分类性能用粗体表示.

由表2 可见，在6 个数据集上WKNNFS 达到的最高分类性能均高于其他方法.当达到最高分类性能时，WKNNFS 在所有数据集上都优于CIFE 方法，即达到最高分类性能时选取的特征数较少.WKNNFS 与另外2 种方法相比，当达到最高分类性能时，在4 个数据集（hcc-data2、Sonar、Prostate 和 brain）上选取的特征数较少，在数据集Q_green 上选取的特征数相差不大，而在数据集clean1 上选取的特征数较多，这可能是因为遗传算法在搜索最优特征权重向量过程中陷入局部最优， 而后又跳出局部最优（由图1（d）WKNNFS 的分类性能曲线可见，在N =13 和N =35附近曲线下降）.

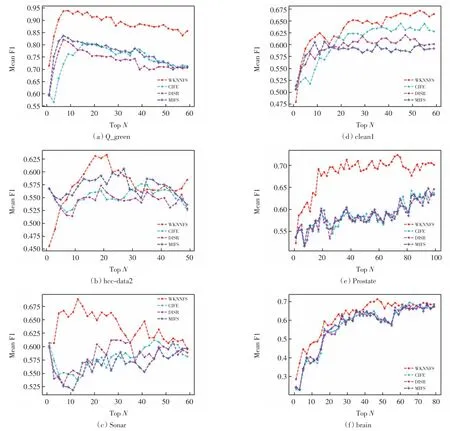
图1 4 种方法在不同数据集上F1 的平均值Fig.1 Mean of F1 on different datasets of 4 methods

表2 在6 个数据集上4 种方法的最高分类性能（F1）及对应的特征数（m）Tab.2 Highest classification performances and the number of features selected of 4 methods on 6 datasets

3 结语

特征选择是机器学习和数据挖掘等领域常用的降维技术.本文提出了基于加权K 近邻的特征选择方法，同时使用遗传算法搜索最优特征权重向量，在6个真实数据集上与其他3 个特征选择方法进行比较实验，结果表明，WKNNFS 获得的分类性能最高，且能较快获得最高分类性能.在未来的工作中可以尝试其他距离公式或遗传算子， 以进一步提高分类准确率，降低预测误差.