2个三能级原子的非平衡热纠缠

孙 悦，郭金良

（天津师范大学 物理与材料科学学院，天津 300387）

量子信息技术[1]的飞速发展给科技带来了新的可能性，同时关于量子力学的研究进入到了空前繁荣的时代.爱因斯坦在研究爱因斯坦-波多尔斯基-罗森悖论（Einstein-Podolsky-Rosen paradox）的过程中正式提出量子纠缠[2-4]的概念，在随后的时间里，作为处理和传递信息的一种新的重要资源，量子纠缠受到众多科学家的广泛研究.近年来， 人们对纠缠态的研究逐渐从封闭量子系统的平衡热纠缠转向开放量子系统的非平衡热纠缠.在开放量子系统中制备和保存纠缠的最大障碍是系统与环境相互作用引起的退相干[5-6].由于一个真正的量子系统是开放的，它不可避免地会受到周围环境的影响，从而使纠缠遭到破坏，因此在研究和制备纠缠态[7]时要考虑周围环境的影响.近年来，相关研究多集中在2 个比特的纠缠动力学，考虑2 个粒子分别与2 个热库相互作用， 以及不同温度情况下，量子纠缠随时间的演化规律[8-10].但现有研究多考虑的是两比特二能级系统，对三能级甚至更高能级的非平衡热纠缠的动力学研究并不多见，因此研究高能级的动力学演化具有重要意义.

本研究采用对数Negativity 的方法对2 个不同玻色库耦合下2 个三能级的开放量子系统的纠缠进行度量[11-12]，首先给出了系统的哈密顿量并用数值模拟的方法得到系统的密度矩阵，然后对非平衡热纠缠随时间的演化情况进行分析，重点讨论了系统的相关参数与初态对该量子纠缠的影响.

1 哈密顿模型

考虑2 个三能级qutrit-qutrit 系统，每个粒子均与2 个独立的玻色库相互耦合，2 个玻色库的温度分别为T1和T2，系统的哈密顿量可以写为[13]

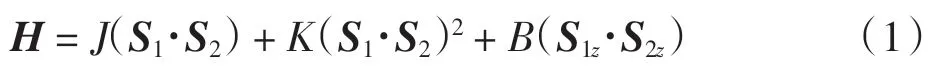
式中：Sα（α=x，y，z）为自旋算符；J 为自旋相互作用的线性耦合强度；K 为非线性耦合常数；B 为沿z 方向的外加磁场.自旋算符的3 个分量（i=1，2）分别取如下形式

用|-1〉，|0〉，|1〉表示基态、第 1 激发态和第 2 激发态.在基失|-1，-1〉，|-1，0〉，|-1，1〉|0，-1〉，|0，0〉，|0，1〉|1，-1〉，|1，0〉，|1，1〉下，可以得到系统的本征值和本征态[13]：

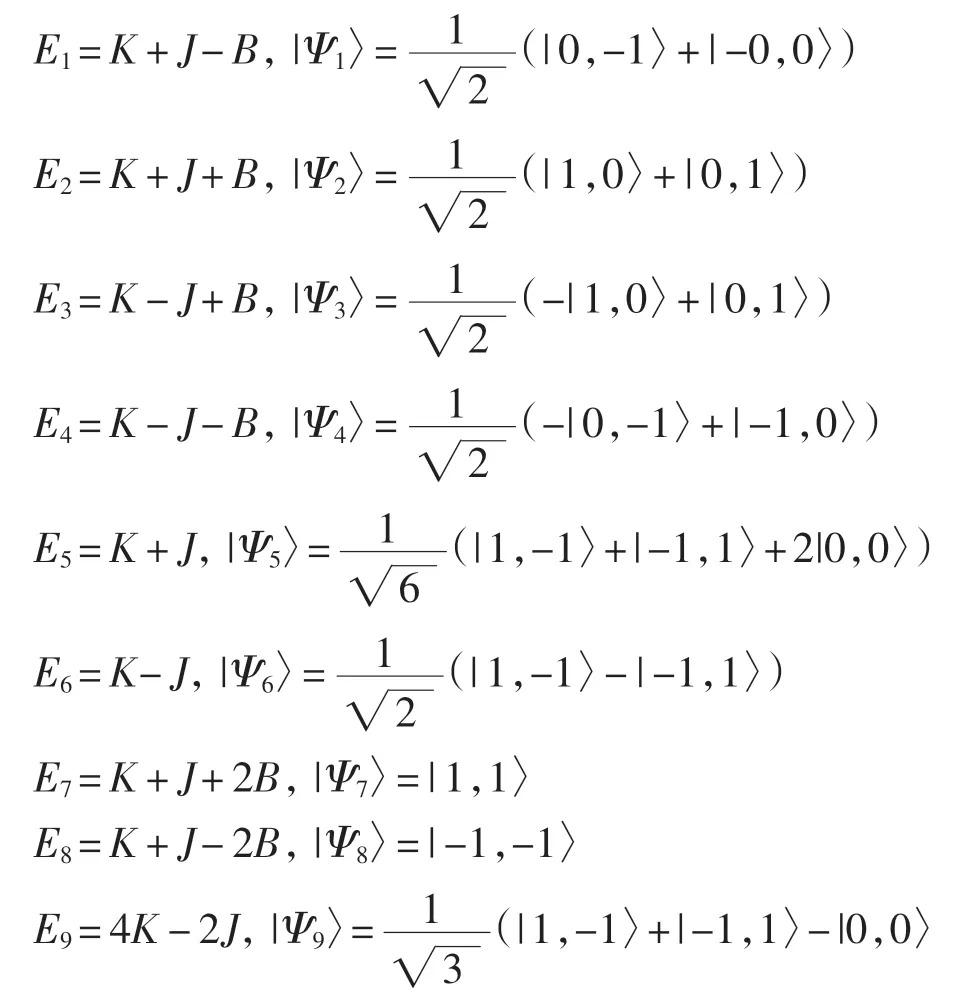
每个自旋粒子（j=1，2）热库的哈密顿量为

为了解决分析问题，只考虑系统与环境间能量交换的影响， 并排除相位差.自旋子系统和玻色库间的相互作用可表示为

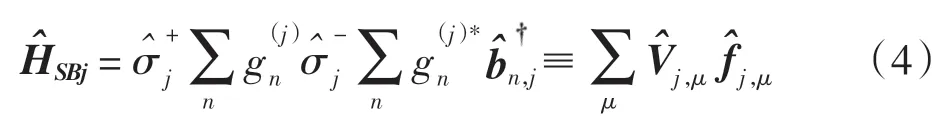
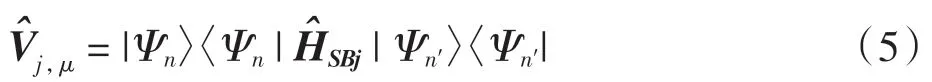
式（5）中：|Ψn〉和 |Ψn′〉为系统哈密顿量的本征态；跃迁频率 ωj，μ可由求得.如果对于相同频率存在不同的跃迁，则需要对与相同频率差相对应的所有跃迁求和.

在系统本征态|Ψi〉的表象下，耗散项可以写为简单形式

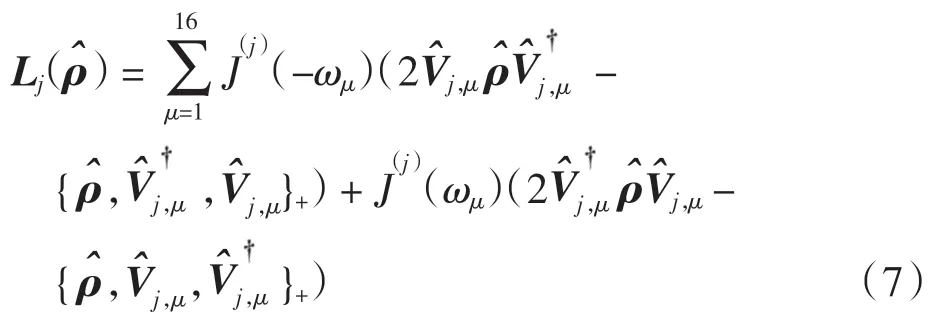
经计算，式（1）中哈密顿量的跃迁算符和跃迁频率可表示为

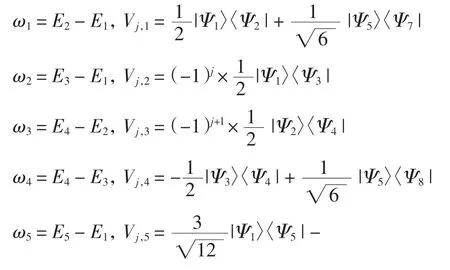
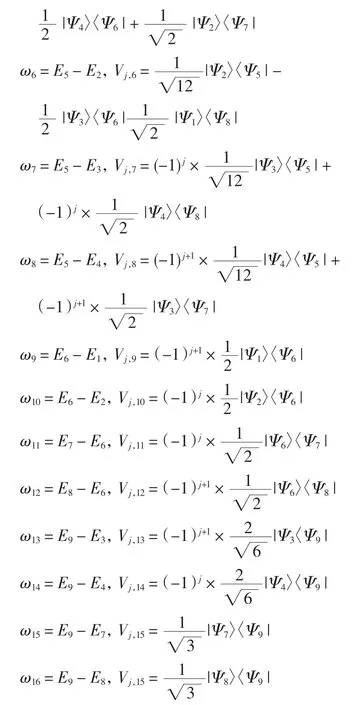
跃迁算符和跃迁频率表达式中，玻色子库被视为一组无限谐振子，因此谱密度变为J(j)（ωμ）=γj（ωμ）nj（ωμ），其中其中βj=1/KBTj（KB== 1）.为了计算简便，常认为γj（ωμ）=γj.

利用波恩-马尔可夫主方程（式（6））计算可得系统密度矩阵对角元的微分方程组，本研究利用数值模拟的方式求解此微分方程组.而非对角元微分方程可以通过简单计算得到解析解.选择系统的初态为

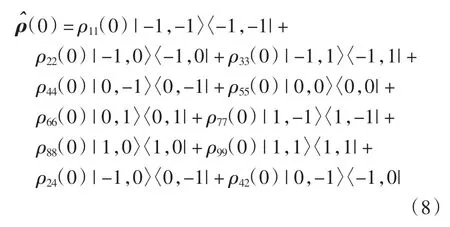
2 非平衡热纠缠

研究非平衡的热纠缠， 一般需要对纠缠进行度量， 进而研究量子纠缠随时间演化过程中的特点.在两比特二能级的自旋系统中，concurrence（并发度）是经常被使用的度量方法[16].但在度量高维Herbert 空间中系统的纠缠时，如本研究中的高能级系统，nega-tivity（负度）是一种有效的度量方法.负度被定义为[17]

粒子分别与2 个不同温度的热库相互耦合，研究在所选的初态下混合自旋系统的纠缠动力学，结果如图1 所示.

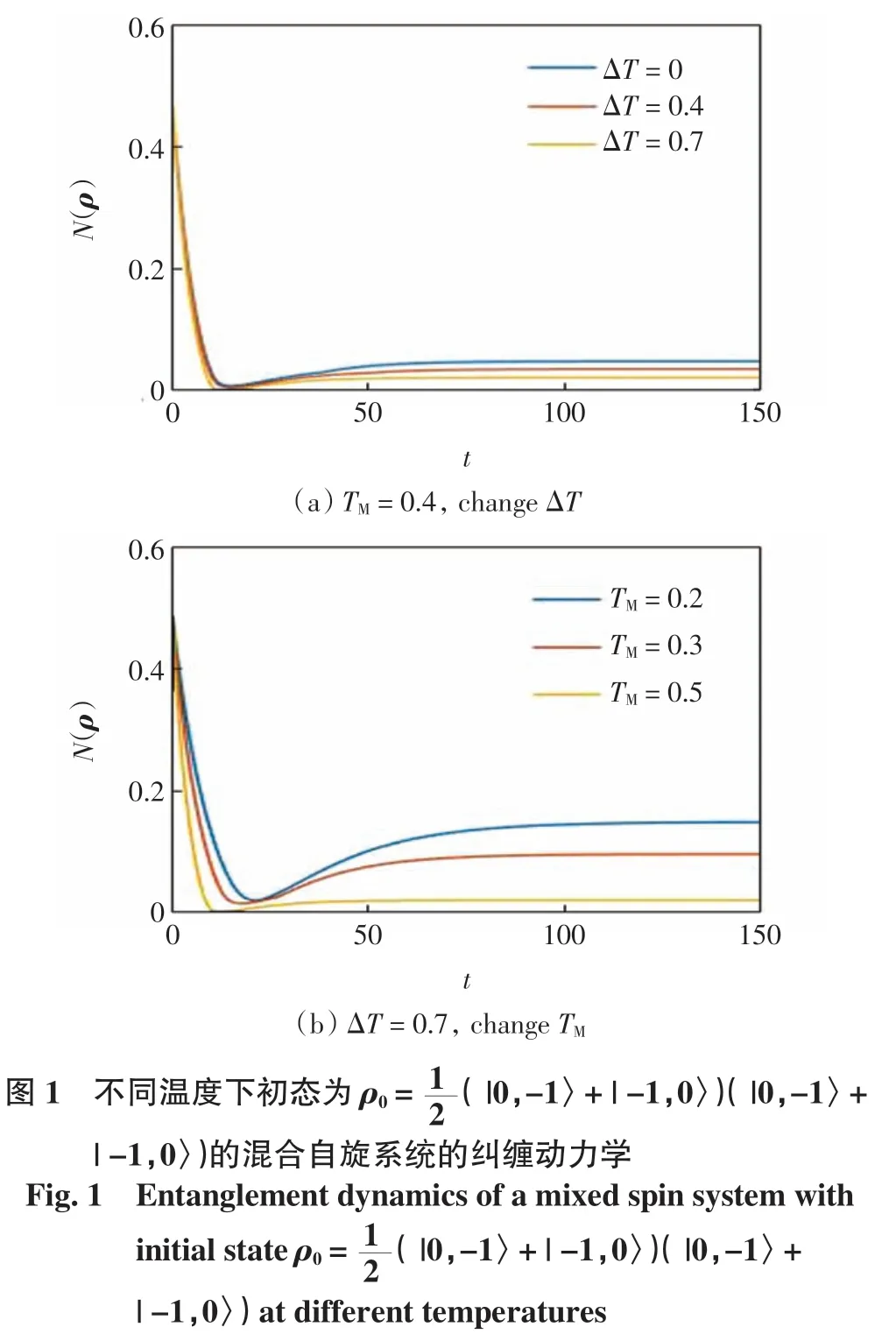
图1 中， 参数 γ1= γ1=0.02，K=-0.3，B=0.4，J=-0.065.图1（a）为在保持平均温度不变的情况下，不同温差ΔT（ΔT = T1-T2）下的纠缠演化，图1（b）为在 ΔT 不变的情况下，改变 TM时的纠缠演化.

由图1 可以看出，纠缠随时间先迅速衰减，随后达到稳定.此外，随着两库温度差ΔT 和平均温度TM的升高，纠缠衰减得越来越快，最终达到稳定纠缠时的值越小.当ΔT 和TM足够大时，如ΔT=0.7 和TM=0.5时，纠缠会在有限时间内消失，即出现纠缠的突然死亡现象[18].减小ΔT 可以在一定程度上增加纠缠的稳定性，说明平衡态的纠缠稳定性优于非平衡态.降低TM会使纠缠猝死现象减弱并消失，从而延缓纠缠减弱的速度.

图2 为不同初态对自旋系统量子纠缠动力学的影响， 其中参数 γ1=γ1=0.02，K=-0.3，B=0.4，J=-0.065，ΔT=0.2，TM=0.4.在初始时刻，可分态 |1，-1〉和|-1，-1〉的纠缠从0 开始演化，初态| 1，-1〉的纠缠在较短的时间内有一个较大的峰值，但持续时间很短.纠缠态的纠缠从 0.5 开始演化，当时间较长时纠缠值趋于稳定.初态| -1，-1〉）的初始纠缠为 1，是最大纠缠态.由图2（a）和图2（d）可以清楚地看到，在 ρ0=|1，-1〉〈1，-1|和 ρ0=（|-1，-1〉）2 种初态下，纠缠在随时间演化的过程中发生振荡，最终达到一个稳定值.这说明在演化过程中两比特之间的能量进行了交换.而由图2（b）和图2（c）可以看出，在 ρ0= | -1，-1〉〈-1，-1|以及| -1，0〉）（|0，-1〉+|-1，0〉）2 种初态下，纠缠没有随时间振荡而是直接达到一个稳态.因此，由图2 可知，无论初态如何，在时间趋近于无穷时，纠缠的稳定值是一致的，说明稳态的大小与初态无关.

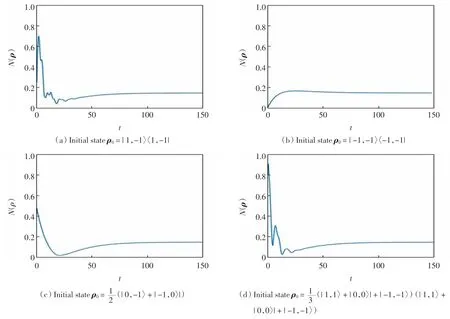
图2 不同初态下混合自旋系统的纠缠动力学Fig.2 Entanglement dynamics of a mixed spin system in different initial states

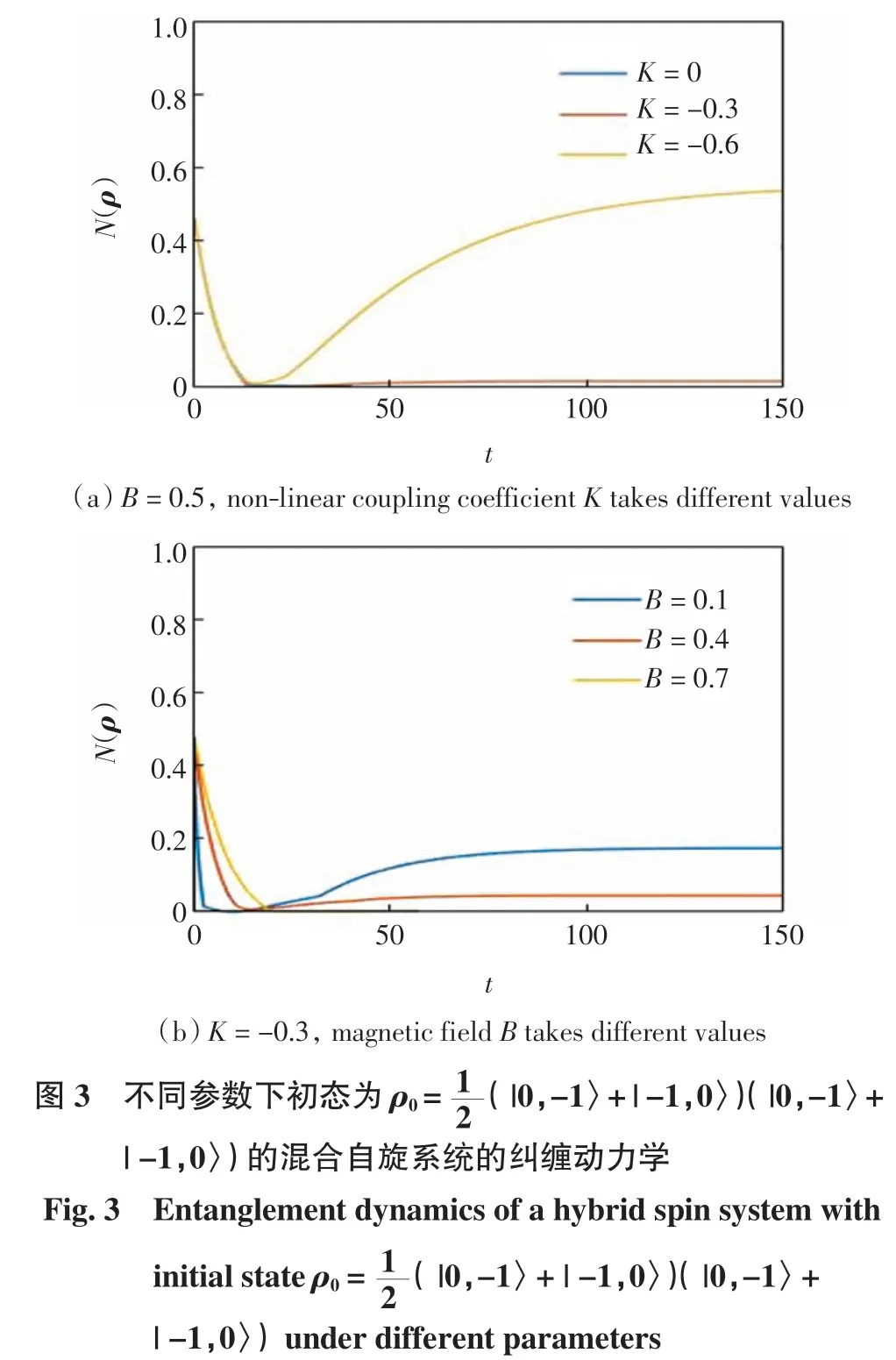
图3 为不同的非线性耦合系数K 和磁场B 对纠缠演化的影响， 其中 γ1= γ1=0.02， ΔT=0.2，TM=0.4.由图3（a）可以看出，当K=0 时，纠缠会突然死亡且不再起复.随着K 绝对值的增大， 纠缠在死亡一段时间后重新出现， 有一个较低的稳定值.继续增大K 的绝对值，当K=-0.6 时，纠缠猝死现象消失，且纠缠的稳态出现非常明显的提高.由图3（b）可知，随着磁场B值的增大，纠缠的稳定性被明显破坏.当B=0.7 时，纠缠在一段时间后消失.B 值若较小，纠缠会在非常短的时间产生猝死，而后随时间的演化稳定在一个比较大的稳定值.综上所述， 非线性耦合常数K 对纠缠的影响是有益的，可以通过提高K 的绝对值得到明显的纠缠， 而磁场B 的存在对纠缠的影响是有害的，B 的增大不仅会降低稳定纠缠甚至会使纠缠彻底消失.

3 结论

本文主要研究了与2 个热库相互作用的三能级qutrit-qutrit 系统的纠缠演化特性，结果表明：

（1）温差ΔT 和平均温度TM的增大均会降低纠缠的稳定性，说明热库温度对量子纠缠的产生及其稳定具有较大的破坏作用，要有效抑制这种退相干，需要适当降低热库的温度.

（2）不同初态的非平衡热纠缠的动力学演化不同，由于两比特间的能量交换，纠缠会随时间发生振动，但尽管初态不同，最后仍能达到一样的稳态值.

（3）非线性耦合常数K 的存在能够给纠缠带来有益的影响，可以通过增大K 的绝对值获得更好的稳定纠缠.而磁场B 会破坏系统的纠缠， 要想获得稳定纠缠可以降低磁场强度的大小.