广义岭估计的一种新的改进方法

殷立爽，范永辉

（天津师范大学数学科学学院，天津 300387）

研究线性回归模型

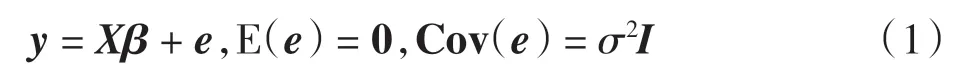
其中：y 为n×1 的随机观测向量；X 为n×p 的设计阵，其秩为p；β 为p×1 的未知回归系数向量；e 为n×1的随机误差向量；σ 为未知参数.

对于回归自变量较多的大型回归问题，回归自变量之间往往存在着近似线性关系，称为复共线性.当设计阵X 存在复共线性时，会使β 的均方误差变得很大，从而使最小二乘（LS）估计的性能变坏，因此有必要对β 进行修正.一个理想的改进方法是在降低均方误差的同时使得均方残差不能增加的太多，为此相关学者做了许多研究[1-7].文献[2]针对最小二乘估计的不足，提出了回归系数的广义根方估计（K），其中K为对角阵，并给出了其显式解.文献[3]针对特征根很小而接近于零的部分，运用压缩最小二乘估计长度的思想提出了岭型组合主成分估计.文献[4]提出了广义岭型组合主成分估计，改变了文献[3]中矩阵对角元素中的岭参数，并给出了岭参数的选取方法.文献[5]针对线性模型中回归系数的估计给出一个估计类：广义压缩最小二乘估计.文献[6]给出了Gamma 回归模型中岭估计的几种改进岭参数.文献[7]提出了logistic 回归模型的限制性岭估计.本文结合岭估计和主成分估计提出了一种广义岭估计的改进方法，在均方误差意义下，证明了改进的岭估计优于最小二乘估计、 普通岭估计和主成分估计.

1 k1，k1，r型岭估计

为方便，引入线性回归模型（1）的典则形式.X′X为正定矩阵， 故可设 λ1≥…≥λp≥0 为 X′X 的特征值，φ1，…，φp为对应的标准正交化特征向量，记Φ=（φ1，…，φp），Φ 为 p×p 的标准正交阵，令 Λ=diag{λ1，…，λp}，于是 X′X= ΦΛΦ′.模型（1）的典则形式为

其中： Z = XΦ， α = Φ′β.Z′Z = Φ′X′XΦ = Λ =diag{λ1，…，λp}， α 的 LS 估计为

2 岭参数的确定

3 k1，k2，r型岭估计与主成分估计的比较

4 算例

λ1、λ2的贡献率为因此确定r=2.采用k1，k2，r 型岭估计来估计回归系数，其迭代法过程如下：

步骤 1： 计算出 α1、α2、 α3的值，作为初始值；

步骤 2： 由式（9）计算 k1和 k2， 利用 k1、 k2， 采用R 语言计算新的 α1、 α2、 α3；

步骤 3： 重复步骤 2， 直至 α1、 α2、 α3的值均趋于稳定时，确定k1和k2.

经计算确定k1=2.80，k2=6.70，进而得到对应的k1，k2，r 型岭估计为

各变量的平均值为

相应地有

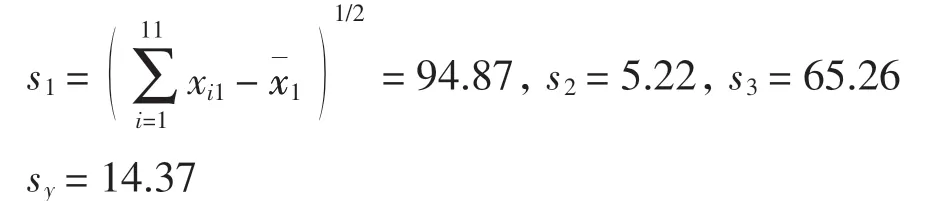
从而得到 k1，k2，r 型岭估计回归方程为

为与其他估计进行比较，表1 给出了LS 估计、岭估计、主成分估计和k1，k2，r 型岭估计回归方程的各项系数.由表 1 可见， k1，k2，r 型岭估计与普通岭估计和主成分估计都比较接近，而与LS 估计相比， x1和x3的系数变化较大，并且x1系数的符号也发生了变化.

表1 算例问题4 种估计的回归方程系数Tab.1 Coefficients of regression equations for 4 kinds of estimator