此处“无声”胜“有声”

吴文祥

【摘要】“缄默知识”由英国哲学家波兰尼提出，其认为缄默知识是更加微妙、不可言说的知识，是一种经常使用，但是不能通过语言文字符号直接传递的知识。在初中数学教学中，相对于显性知识而言，教师对缄默知识的传递往往能够实现一种此处“无声”胜“有声”的效果。文章对此做出了相关介绍。

【关键词】此处无声胜有声;初中数学;缄默知识;传递

一、前言

数学是一门对学生理性思维要求很高的学科，很多知识与智慧是在无声无息的积累中生成的。缄默知识又被称为“内隐知识”，是人认识事物、解决问题过程中所依赖的一种理解和自信。在初中数学教学中，教师能够将缄默知识有效地传递出去，往往可以实现一种此处“无声”胜“有声”的效果，对学生的数学成长发展会产生诸多裨益，是今后教师教学研究的重点。

二、感知存在是缄默知识传递的基础

缄默知识是一种不可名状的知识，它存在于人的认知过程中。在初中数学教学中，缄默知识虽然看不见，摸不着，但是无处不在。教师若想要对缄默知识进行传递，就必须要先使学生感知缄默知识的存在。学生只有认识到缄默知识是真实存在的，才愿意深入地挖掘缄默知识，并重视缄默知识的学习。如笔者在执教过程中，会通过“直接”和“间接”两种形式帮助学生感知体会缄默知识的存在，从而实现此处“无声”胜“有声”的教学效果。

1.直接法

所谓“直接法”，主要是指教师通过想象比喻、生活转换和PPT整合的方式，尽可能地将缄默知识形象化，从而促使学生理解缄默知识的含义，帮助学生直观地认识缄默知识。如笔者就曾经用了这样一个比喻直观地阐述缄默知识：人在走路的过程中，有的人并没有强化记忆，但是对于之前走过的路了如指掌;有的人努力记忆，却犹如“路痴”，即使走了很多遍，也不记得走过的道路。这就是缄默知识的体现[1]。在解答数学问题的过程中也是如此。缄默知识就好比“思路”，有了缄默知识，可以快速地调取脑海中的公式法则，即使对于指向性不强的问题，也可以快速地得出答案。因此在初中数学学习过程中，缄默知识是无处不在的。像这样的例子还有很多，在实践教学过程中，教师要借助直接刺激的方式，帮助学生理解缄默知识的含义。

2.间接法

所谓“间接法”，就是让学生在潜移默化的过程中感知缄默知识的存在，让学生认识到缄默知识是数学世界中最美的知识。如英国数学家哈代就曾经说过：“数学的美是难以定义形容的，但是一种真实存在的美。”这其实就是数学缄默知识的美[2]。如在初中数学学习中，“对称轴”“函数曲线”“平面几何”都是存在一种真实之美的，这种美虽然用语言无法描述，但是在心灵上可以认知体会。在实际教学过程中，教师要不断地对学生进行间接引导渗透，帮助学生感知缄默知识的存在，并体会到缄默知识是介于逻辑思维与直觉思维之间的一种思维形式。这种思维形式是学习数学知识的重要突破口，也是缄默知识真实存在的一种证明。

三、挖掘作用是缄默知识传递的保障

在初中数学学习过程中，缄默知识的学习是具有重要意义的。相比较显性知识，教师对缄默知识的传递，更能实现一种此处“无声”胜“有声”的教学效果。在教育改革的新形势下，教师要更新传统守旧的教学观念，注意对缄默知识的作用进行挖掘，推动学生数学学习的更好发展。对此，笔者提出以下几个方面的建议。

1.概念教学，留有余地

概念是数学知识的基本依据，在初中数学教学中，理解数学知识概念，是学生学好数学的先决条件，同时也是学生做题、解题的基础。以往教师在对学生进行概念教学时，总是恨不得将所有的知识都展现出来，不留余地地全盘灌输给学生。这种教学方式看似毫无保留，但由于没有激发调动学生的主动思维意识，反而对教学效果造成了一定的负面影响。以“三角函数”知识教学为例，这一知识在中考计算题中的出现频率很高。初中阶段学生需要掌握30°、45°、60°特殊的三角函数值，如表1。

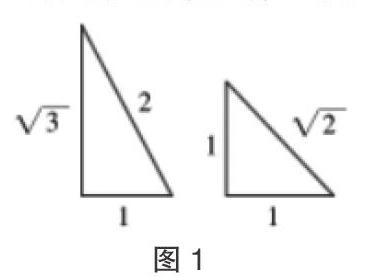
以往在讲解这一知识时，很多教师都是将上述三角函数值直观地展示出来，并让学生进行背诵记忆，但在实际应用的过程中，学生还是容易混淆遗忘。而在缄默知识传递教学中，教师无需向学生出示三角函数值，只需将图1所示的图形展示出来即可，然后引导学生观察图形，借助两个特殊直角三角形的特殊边长自行求解，为学生提供一个获取缄默知识的空间，从而通过图形对照的方式，记忆不同角度对应的三角函数值。在这样的教学方式下，知识不是教师直接喂到学生嘴里的，而是学生自己掌握和消化了知识概念，形成缄默知识，帮助学生形成永久性的记忆，可以帮助学生减少知识遗忘，为学生的学习提供了保障[3]。

2.数学阅读，学会分析

阅读不仅是语文或者英语学科的学习专利，初中数学学习中也是需要阅读的。良好的阅读能力是学生数学学习、理解的保障。然而在教学过程中教师都有这样的心得体会，就是数学阅读能力培养无从入手，无法对学生进行系统的指导，只能学生自己体会分析，这其实就是数学缄默知识传递的过程。

如在进行“垂径定理”教学时，“垂直于弦的直径平分弦，并且平分弦所对的两条弧”叫作“垂径定理”，这一定理内容虽然只有21个字，但是多数学生难解其意。虽然结合图形教学可以在一定程度上改善效果，但依旧存在一定的局限性。对此，在传递缄默知识的教学中，教师可以采用这样的方式对学生进行引导，如要求学生像阅读古诗一样，对 “垂径定理”概念进行阅读，如“垂直于弦的/直径/平分/弦，并且/平分/弦所对的两条弧”，这样的阅读方式能够更好地帮助学生把握住定理内容中的關键词，以及句子中主谓语之间的关系，然后教师再结合图形指导阅读，学生就会更加清晰地理解体会“垂径定理”知识[2]。在这样的阅读分析引领下，学生可以自然而然地体会如何在阅读中“抓重点”，从而促进学生数学阅读能力的提升。除此之外，教师还可以传授学生圈画法、问题罗列法等提高数学阅读能力的方法。这就是无形中将积累缄默知识方法传递给学生的一种体现。随着学生阅读能力的不断提升，学生的数学学习之路也会走得更加顺畅，从而实现了一种此处“无声”胜“有声”的教学效果。

3.问题解决，重视方法

在初中数学教学中，很多教师都反映学生的解题能力不强。导致此种现象的重要原因就是学生缺少缄默思维。可以说，在解决数学问题时，缄默知识的运用是解题的第一步，具有缄默知识的学生会自己思考“如何解决”，从而快速地确定解题思路，找到解题的突破口。

例如：“在直角坐标系xOy中，点O的坐标为（0，0），有一个动点A，坐标为（t，t），在第一象限，动点B（0，m）在y轴上。当AB=4时，问△OAB面积的最大值为多少？”在解答这样的数学问题时，大多数学生根据自身的缄默知识，第一反应就是建立直角坐标系，但是在建立直角坐标系之后发现无法更进一步解题，因此陷入解题困境。正确的解题思路应该为将O、A、B三点置于圆中，当点O到AB的垂线段经过圆心时，此时的三角形面积就是最大的。而在对学生进行缄默知识传递时，显然不能直接将这一解题思路告知学生，教师可以通过侧面引导的方式，逐步地帮助学生建立解题思路。

如教师可以引导学生做出这样的思考，即△OAB中∠O是一个固定值45°，AB的长度4也是确定的，只有点O是一个动点，它与AB的位置关系不断地发生变化，正是因为有了这样的变化，△OAB的面积才发生了变化。问题转化为：在圆中长为4的定弦AB所对的圆周角∠O是45°，求动点O到直线AB的最大距离。这样的引导会让学生思考“是什么元素决定了三角形的面积呢？”在思考的过程中，学生就会逐步树立正确的解题思路。这就是教师向学生传授缄默知识的一种体现。

在整个初中阶段的数学学习中，解题方法很多都是固定的，如直接法、补形法、分割法等。缄默知识的传递，使学生对解题方法进行积累，对学生的数学学习成长有诸多裨益，可促使学生的解题能力不断提高，实现此处“无声”胜“有声”的教学效果。

四、结语

相比可以直接用语言、文字、符号直接表达的显性知识，缄默知识则隐形地存在于人的认知过程中，其虽然“不可名状”，但是是真实存在的。在初中数学教学中，教师对缄默知识进行传递，可以更好地帮助学生领悟知识精髓，实现一种此处“无声”胜“有声”的教学效果，因此缄默知识传递是值得今后广大初中教师同仁探索研究的课题。

【参考文献】

[1]薛峰.此处“无声”胜“有声”——浅谈初中数学教学中缄默知识的传递[J].数学教学通讯，2019（14）：38-39，51.

[2]李光友.此时无声胜有声——浅谈初中数学问题教学中学生思想品质的培养[J].学生之友（初中版）下，2016（07）：67.

[3]陆一黎.此时无声胜有声——缄默知识在美术教学中的运用淺探[J].中国美术教育，2011（03）：4-7.

[4]曹焱.发展学生数学素养，“板书”无声胜有声——结构式板书在初中数学素养教学中的探索与实践[J].数学教学通讯，2019（11）：74-76.