弹簧摆到底能摆多高?
——由一道高三联考题引发的思考和研究
2020-04-23江俊勤
江俊勤
(广东第二师范学院物理与信息工程系,广东 广州 510303)
1 衡中同卷——2019年全国高三联考理综卷第21题及其答案
图1 弹簧与小球的初始状态

(A) 弹簧的最大长度大于L.
(B) 小球到达的最高点高于O点.
(C) 小球到达的最高点与O点等高.
(D) 小球到达最高点时弹簧弹力为0.
试题答案与解析: (A)、(B).

2 用机械能守恒定律做定性分析
原考题所给的答案“选项(B)正确,(C)错误”明显是一个想当然的武断结论、其解析也逻辑混乱,错误地认为开始时系统的机械能mv02/2+EpF>mgL就保证了小球到达的最高点高于O点. 在原题答案的解析中,明显漏掉了最高点处小球可能有较大的动能mvx2/2 (x为水平方向,y为竖直方向,O为坐标原点;如图2所示),也没有考虑小球在最高点时的弹力势能,这两项的大小将直接影响着小球所能到达的高度,下面先从机械能守恒定律出发进行定性分析.
设弹簧的劲度系数为k,松弛状态(自然状态)的长度为L0,最高处小球的纵坐标为ymax、弹簧的长度为l;以小球的初始位置为重力势能的零点,则开始时系统的机械能为mv02/2+EpF=mv02/2+k(L-L0)2/2>mgL;在最高点处系统的机械能为mvx2/2+k(l-L0)2/2+mg(L+ymax).由机械能守恒定律得
mv02/2+k(L-L0)2/2=mvx2/2+k(l-L0)2/2+mgL+mgymax.
(1)
式(1)右边前两项mvx2/2和k(l-L0)2/2的大小都是未知的,从题设条件我们并不知道mv02/2+k(L-L0)2/2是比mvx2/2+k(l-L0)2/2+mgL大还是小,故不能确定ymax>0还是ymax≤0,即无法保证小球到达的最高点高于O点!
小球到底能摆多高?小球到达的最高点能不能高于O点?为了彻底解答本问题,必须从牛顿第二定律出发进行定量分析.
3 动力学方程和数值分析
(2)
由牛顿第二定律可知摆球的动力学方程为
(3)
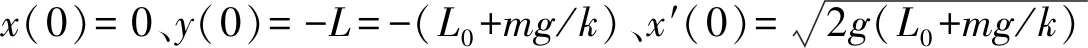
本文固定取m=0.1 kg,L0=0.5 m,而k取各种不同数值进行求解. 先取较小的劲度系数,例如k/m=110 N/(m·kg)(即m=0.1 kg、k=11 N/m),则摆球在1.5 s、12 s和180 s内的运动轨迹分别如图2~4 所示,球到达的最高点自始至终都低于O点,即选项(B)“小球到达的最高点高于O点”是不能实现的.
小球处于平衡时合力为0,突然获得一水平速度后沿水平方向做直线运动并开始拉伸弹簧(所以选项(A)正确),随着弹簧长度增加拉力增大,小球向上做曲线运动(然后弹簧开始处于压缩状态);第一次到达最高点(严格来说应称为y的极大值点)处之后受外推弹力作用向右下方运动,第一次到达最低点处(y的极小值处)在惯性和弹簧力拉扯下向左上方向运动,并跨越中线(x=0)到达左边,如图2所示,在1.5 s内小球的运动轨迹开始呈现出“上下左右反复”的复杂性;图3给出了12 s内的运动轨迹,小球的运动轨迹杂乱无章、左右不对称;但经历足够长的时间后,运动轨迹表现出规律性——小球运动轨迹被限制在某种带状的有限区域内并呈现出大体上的左右对称,180 s内的运动轨迹如图4所示.

图2 当k/m=110 N/(m·kg)和L0=0.5 m时,小球在1.5 s内的运动轨迹
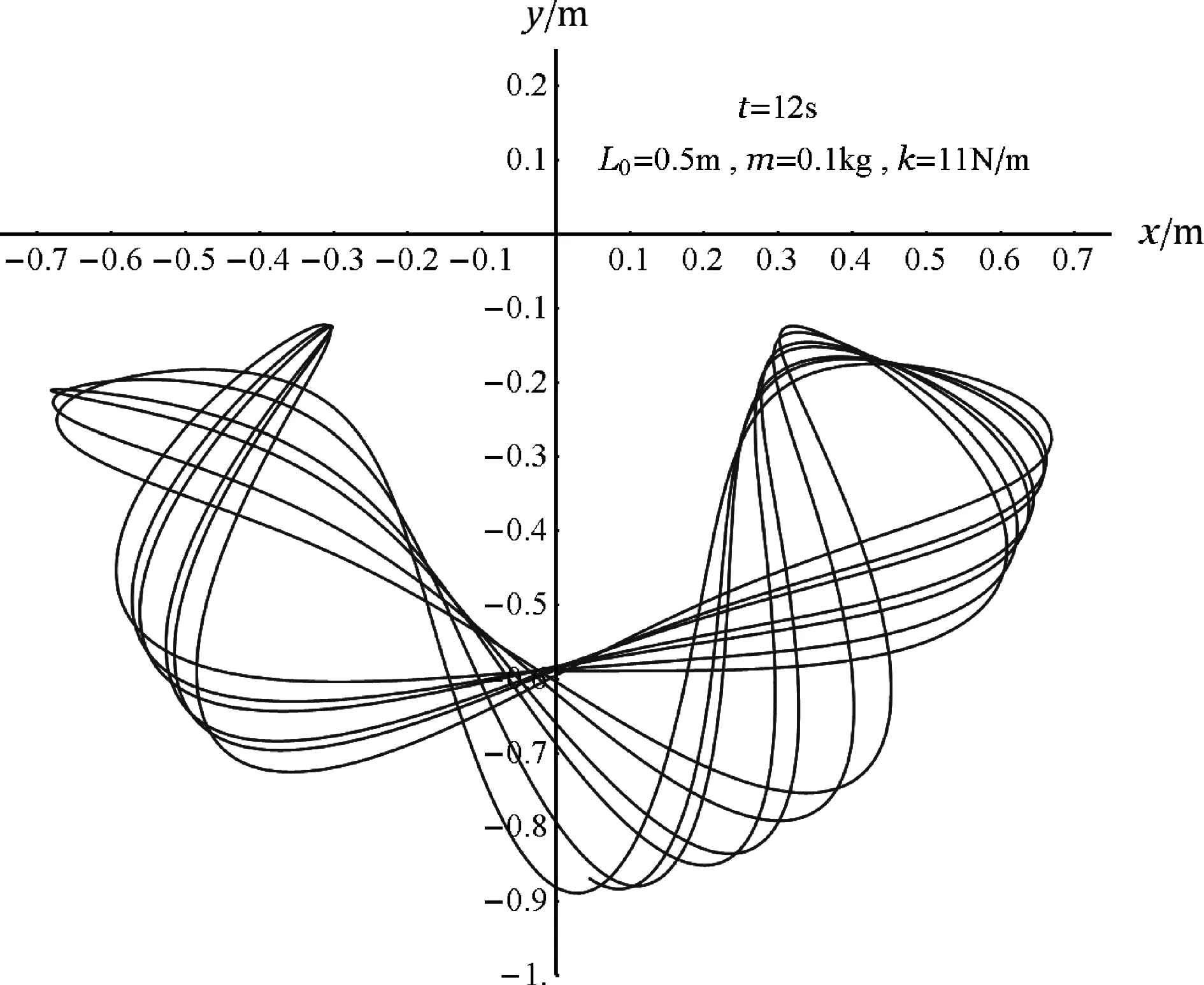
图3 当k/m=110 N/(m·kg)和L0=0.5 m时,小球在12 s内的运动轨迹
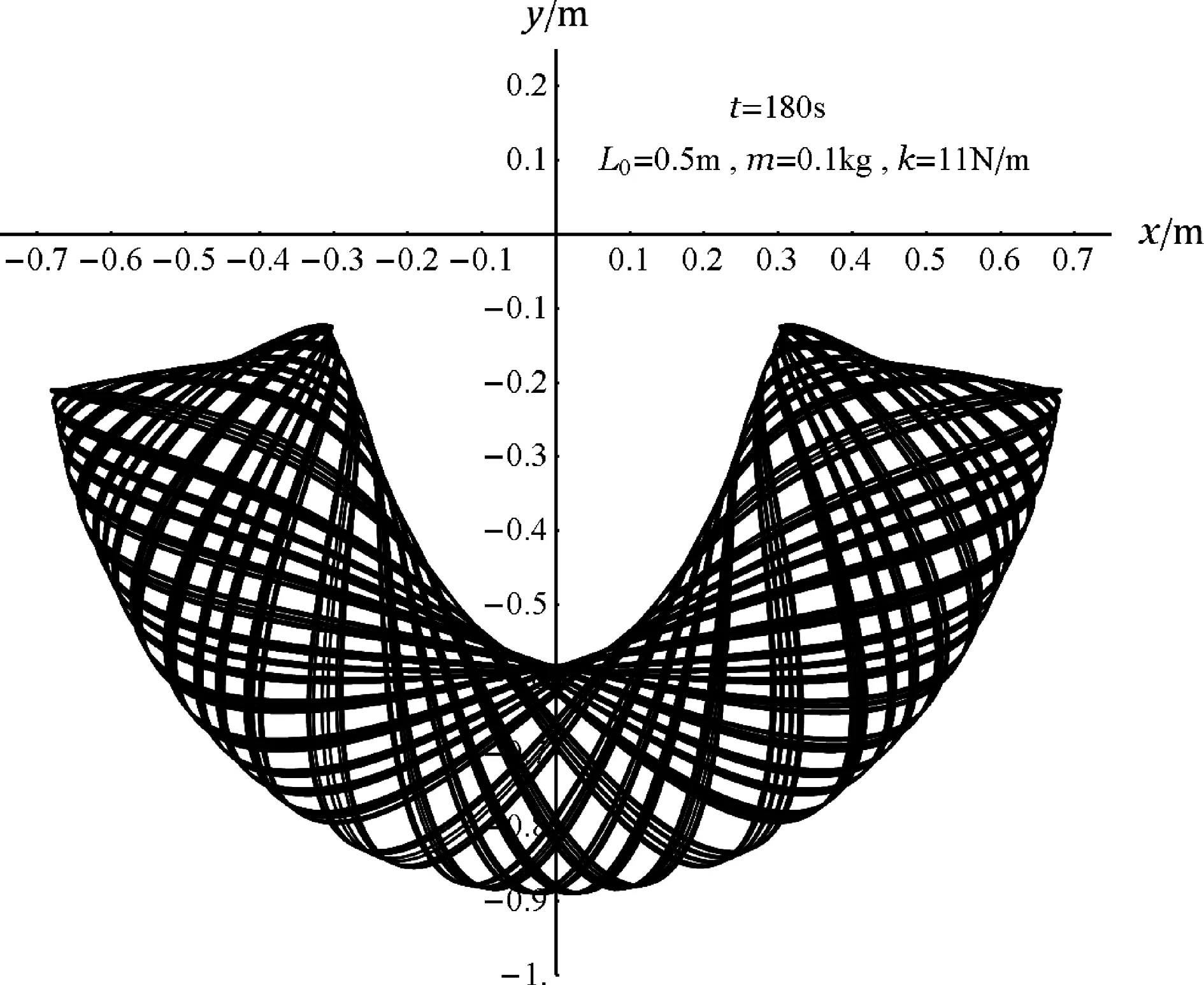
图4 当k/m=110 N/(m·kg)和L0=0.5 m时,小球在180 s内的运动轨迹
图2~4显示:当k/m=110 N/(m·kg) 时, 最高点处小球具有较大的动能mvx2/2或较大的弹力势能k(l-L0)2/2,所以虽然mv02/2+EpF>mgL,但小球的最高点低于O点(ymax<0). 更多的模拟表明在k/m≤134 N/(m·kg) 时都是如此.
若取大一些的劲度系数, 如k/m=150 N/(m·kg)(即m=0.1 kg、k=15 N/m), 则摆球在1.5 s、3.5 s、12 s和180 s内的运动轨迹分别如图5~8 所示.
从图5~图8可知,当k/m=150 N/(m·kg) (即m=0.1 kg和k=15 N/m)时,能实现摆球到达的最高点高于O点. 但是,在小球向上运动的过程中,不是每次摆到“最高点(严格来说是高处反转点或y的极大值)”都高于O点,更不是一开始就能高于O点:图6显示直到第3.5 s前夕的第四个高处反转点时才第一次出现高于O点的机会,图7表明前12 s内才有两次出现高于O点的情况(当ymax>0时该极大值点处小球的动能和弹力势能都较小).
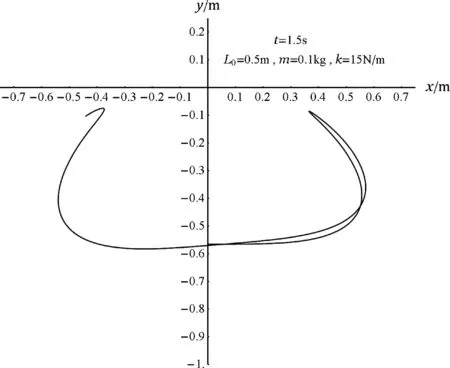
图5 当k/m=150 N/(m·kg) 和L0=0.5 m时,小球在1.5 s内的运动轨迹
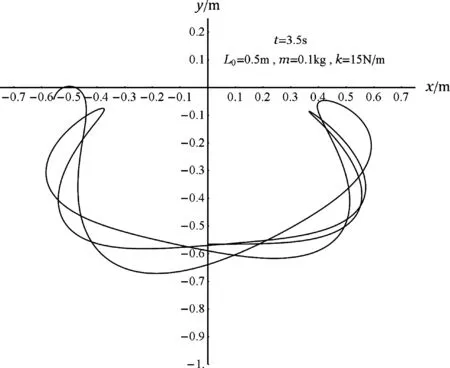
图6 当k/m=150 N/(m·kg)和L0=0.5 m时,小球在3.5 s内的运动轨迹

图7 当k/m=150 N/(m·kg)和L0=0.5 m时,小球在12 s内的运动轨迹

图8 当k/m=150 N/(m·kg)和L0=0.5 m时,小球在180 s内的运动轨迹
进一步的数值结果表明:只要134 N/(m·kg) 取更大的劲度系数,例如k/m=200 N/(m·kg) (即m=0.1 kg 、k=20 N/m),则摆球在180秒内的运动轨迹如图9所示,小球到达的最高点又是都低于O点. 图9 当k/m=200 N/(m·kg) 和L0=0.5 m时,小球在180 s内的运动轨迹 本文先从机械能守恒定律出发对2019年全国高三联考理综卷第21题进行了定性讨论,结果表明:从机械能守恒定律出发无法判断摆球到达的最高点能不能高于O点,考题的原答案及其解析都是欠妥的. 为了让问题有明确的答案,本文接着从摆球遵循的牛顿第二定律出发、使用著名通用软件Mathematica对该问题进行具体深入的数值计算和检验,由具体的计算结果可以得出如下结论: (1) 选项(A)“弹簧的最大长度大于L”是正确的. (2) 选项(B)“小球到达的最高点高于O点”不一定能实现,只有小球质量m和弹簧劲度系数k满足某些特殊条件才能实现,若取m=0.1 kg和L0=0.5 m,则只有劲度系数在较狭窄的范围内13.4 N/m (3) 既然在m和k满足某些特殊条件可以实现小球到达的最高点高于O点,那么选项(C)“小球到达的最高点与O点等高”的可能性就不能完全排除在外. 总之,小球到达的最高点能否高于O点由弹簧的自然长度L0和劲度系数与小球质量的比值k/m共同决定,本考题的原答案及其分析都是不对的,它给物理教师的警示是:在设计新型题目时务必小心谨慎,最大限度地避免“想当然”. 公开推出新题之前应该从大学物理的高度认真审视其科学性,如果遇到没有简单解析解而无法得出明确结论的情况,则最好能利用通用软件进行数值检验.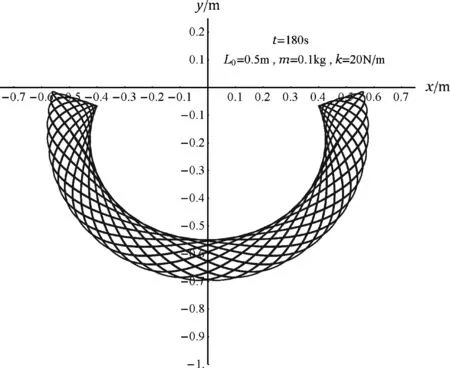
4 结论与讨论
