中心引力场下天体运动的椭圆轨道证明

王 磊

(盘锦市高级中学,辽宁 盘锦 124000)

天体运动是高中物理必修2的内容,之前学生已经掌握了圆周运动和功能关系等辅助学习天体运动的物理知识. 天体运动首先从开普勒的三大定律讲起,而开普勒三定律的得出并未做任何理论推导,这使得教师主要以灌输的方式教,学生以记忆的方式学.“为什么是椭圆?”、“为什么扫过的面积是相等的?”、“为什么是和半长轴的立方成正比而不是短轴?”这些得不到答案的问题让以椭圆为基础的开普勒三定律显得尤为神秘,尤其是当遇到天体运动的椭圆问题时,学生更是觉得不可捉摸,难以处理.而在物理竞赛以及自主招生物理考试中,关于天体运动椭圆轨道的考察又较为常见,所以在相关物理教学中对天体运动椭圆轨道的证明和展开讲解是有必要的.

1609年年轻的德国科学家开普勒猜测行星沿椭圆轨道运动,开普勒发现他老师弟谷观测的火星运行数据无论是用哥白尼的日心说圆轨道理论还是托勒密的地心说本均轮轨道理论都不能很好匹配,唯有椭圆形轨道才能完美解释老师观测的火星位置数据.[1]这样开普勒提出了他的第一个伟大发现“椭圆定律”并相继发现了“面积定律”,10年之后才提出他的“周期定律”.[2]

开普勒之后,对天体运动的研究吸引了很多物理学家,比如伽利略、布里阿德、惠更斯、哈雷、胡克等,[3]他们对于圆周运动向心力,星体间引力与星体间距离平方成反比等天体运动相关理论研究均有一定的贡献,但真正在天体运动研究领域光芒盖过开普勒的是在其3大定律提出后半个多世纪——在其3大定律基础上发展得出更具普适性的万有引力定律的牛顿.不仅如此,牛顿用其发明的微积分数学方法证明了与有心力场中心距离平方成反比的引力场中物体的运动轨迹为椭圆.这是对开普勒“椭圆定律”的第一次完备的数学证明.[4]但牛顿在其著作《自然哲学的数学原理》书中所应用的微积分方法是以几何的形式出现的,后来,拉格朗日、哈密顿等人对经典力学进行形式上的改造,大规模使用现代微积分方法而排斥初等几何学,但其物理思想并没有超出牛顿的框架.

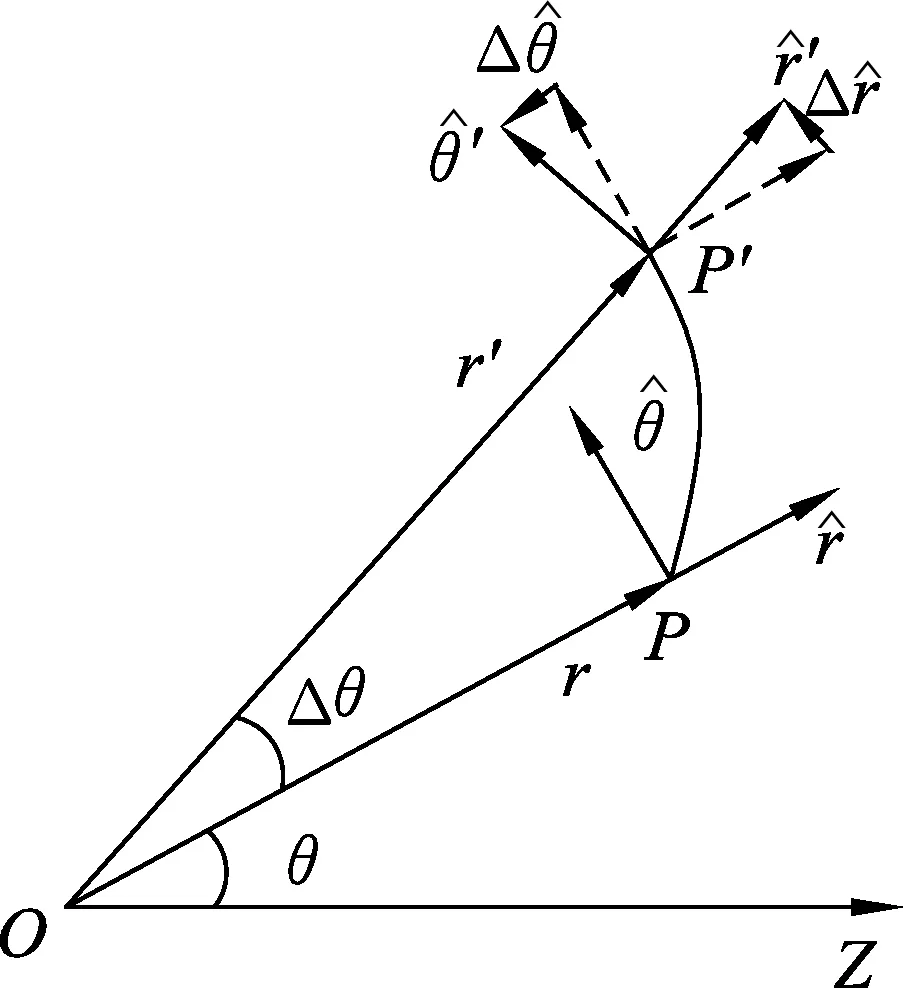
图1 极坐标下运动学

1 平面极坐标下运动学

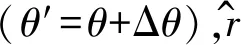
(1)

(2)

在极坐标系OZ下研究物体运动到P点时的位置、速度、和加速度有:[5]

(2) 物体在P点的速度为

(3)

写成微分形式有

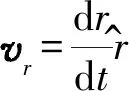
(3) 物体在P点的加速度为

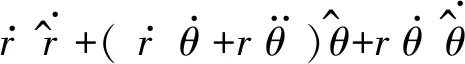
代入(1)、(2)式得

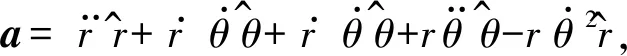
(4)

(4)式写成微分形式有

2 极坐标下天体运动轨迹方程

径向:

(5)

横向:

(6)

由环绕天体运动在有心力作用下角动量守恒,有心引力场下L为定值,有

可得

(7)

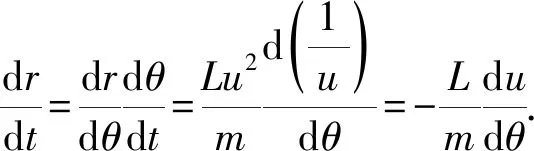
(9)

将(7)、(9)式代入(5)式可得

整理得

(10)

该方程为二阶齐次常微分方程,其解为

(11)

该方程是否为椭圆方程呢?

3 椭圆轨迹方程在笛卡尔坐标系和极坐标系下的转换

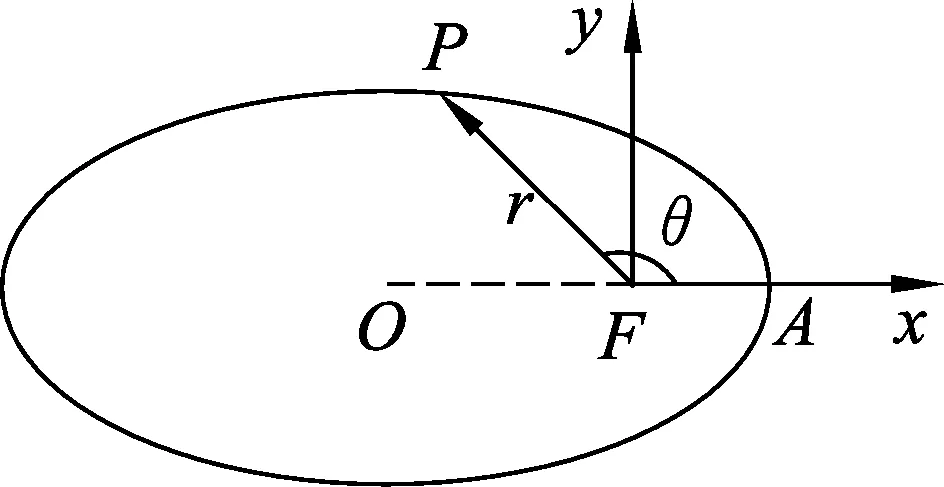
图2 笛卡尔坐标与极坐标下椭圆

(12)

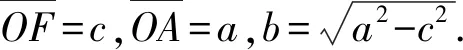
(b2r2cos2θ+a2r2sin2θ)+2cb2rcosθ+(b2c2-a2b2)=0.

整理得

r2(b2cos2θ+a2-a2cos2θ)+2cb2rcosθ-b4=0,

进一步整理得

r2(a2-c2cos2θ)+2cb2rcosθ-b4=0.

(13)

该方程为r的二次方程,应用韦达定理可得其解为

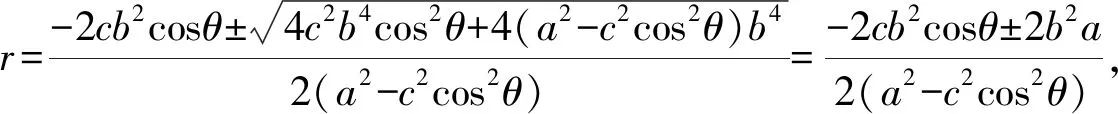
由r>0有

(14)

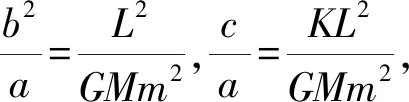
4 引力场下椭圆轨道方程的确定

某环绕天体椭圆轨迹(图3),设其椭圆长轴A1A2=2a,短轴B1B2=2b,两焦点距离F1F2=2c,中心天体位于右焦点F1处.根据图像有F1P=r，F2P=2a-r、∠F1PF2=π-2θ,[6]在ΔF1PF2中运用余弦定理有

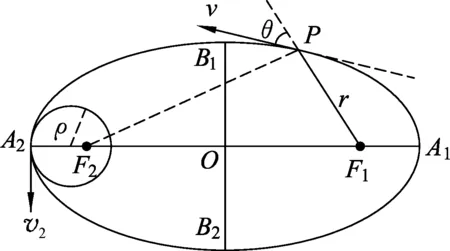
图3 椭圆轨道及其曲率圆

r2+(2a-r)2-2r(2a-r)cos(π-2θ)=

(2c)2,

(15)

(3)式结合a2=b2+c2以及三角函数公式

cos(π-2θ)=-cos2θ=2sin2θ-1,

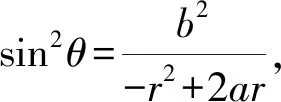
(16)

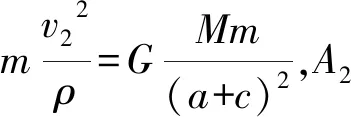
(17)

(18)

将(16)、(17)式代入(18)式可得

(19)

质量为M的中心天体引力场下,质量为m的环绕天体的轨道能E(E<0)与角动量L已知,以椭圆中心为坐标原点,长轴为x轴,短轴为y轴的笛卡尔坐标系中，则其运动轨迹方程为

其中E<0.

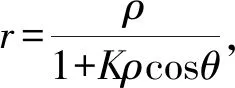
总结:本文在极坐标下得到了万有引力作用下环绕天体的运动轨迹方程,并通过笛卡尔坐标系与极坐标系下椭圆方程的转换,对比得出中心天体引力作用下环绕天体的运动轨迹方程为椭圆.该椭圆轨道由环绕天体角动量和轨道能确定.最后本文给出了基于角动量和轨道能的笛卡尔坐标系下与极坐标系下的椭圆轨道方程.