基于有限元分析的螺纹连接强度设计技术研究

李俊岩，包婷萍，侯鹏飞，成兆义，陈安平

基于有限元分析的螺纹连接强度设计技术研究

李俊岩，包婷萍，侯鹏飞，成兆义，陈安平

（北京精密机电控制设备研究所，北京，100076）

通过对螺纹连接强度的研究，确定适用于航空航天等对轻量化具有较高要求领域的螺纹连接优化强度设计方法。采用有限元分析方法对螺纹牙的强度校核进行了仿真分析，通过提取螺纹牙的接触力获得了螺纹连接的承载力分布规律，为传统螺纹强度计算中的旋合圈数提供了新的解决途径。

有限元分析；螺纹牙；接触力

0 引 言

螺纹连接是一种广泛使用的可拆卸固定连接方式，具有结构简单、连接可靠、拆卸方便等优点。传统的设计方法对于螺纹的旋合圈数没有给出具体的确定方法，而选取的旋合圈数与螺纹牙应力强度校核值成反比例线性关系，旋合圈数选取过小，使螺纹公称直径选用过大，导致产品质量增加；旋合圈数选取过大，使螺纹牙应力校核值较真实值偏大，存在螺纹失效的风险。本文基于现代先进有限元分析方法，对螺纹受力进行分析，并得出螺纹接触力与旋合圈数的关系，为螺纹强度设计提供理论依据。

1 螺纹连接传统设计方法

螺纹牙的受力分析，传统的设计方法是将螺纹牙展开后，将其视为悬臂梁，外螺纹及内螺纹展开受力示意分别如图1、图2所示。螺纹牙承受沿螺栓轴向的载荷力，根据集中力的原则，则力的作用点位于螺纹牙中径。

图1 外螺纹展开受力示意

图2 内螺纹展开受力示意

外螺纹的剪切应力为

内螺纹的剪切应力为

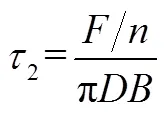
外螺纹的弯曲压力为

内螺纹的弯曲压力为

外螺纹的挤压应力为

内螺纹的挤压应力为

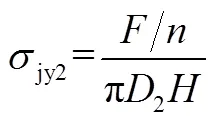
传统的螺纹牙校核方法为根据单个螺纹的受力，对内、外螺纹牙的剪切、弯曲及挤压应力进行计算，其中螺纹牙的应力与旋合圈数成反比例线形关系，因此，螺纹圈数的确定是螺纹牙校核的关键，传统的设计方法一般认为旋合圈数为3～10，应力的误差散布非常大，往往造成螺纹选用过大或过小，尤其是对于产品的质量限制比较严格的航天领域，给产品设计人员造成较大困扰。

2 有限元仿真分析方法

由于传统的理论计算仅能够反映螺纹连接处的综合受力情况，不能够真实地反映螺纹旋合圈数对螺纹牙的强度影响，因此，本文采用ANSYS Workbench有限元分析软件对螺纹连接进行仿真分析，提取每圈螺纹牙的接触力，并进行统计分析，梳理出接触力与螺纹旋合圈数的关系。

2.1 建立数字化三维模型

首先，采用CREO三维设计软件建立简化数字化模型，模型主要由螺孔（内螺纹）、螺栓（外螺纹）以及连接件3部分组成，其螺纹牙为标准三角形螺纹，具体结构如图3所示。

螺纹牙多圈模型采用单圈阵列方式，将每圈螺纹作为单独特征，便于实现ANSYS有限元分析每圈螺纹接触定义以及螺纹接触力的提取。

图3 螺纹连接简化模型

2.2 有限元模型参数设定

通过CREO与ANSYS Workbench仿真接口将三维模型导入ANSYS Workbench仿真环境，对模型进行材料设定、接触设定、网格设定、载荷约束设定以及模型求解。

2.2.1 材料参数设定

为确定不同材料对螺纹接触力的影响，根据航天伺服系统的常用材料，本文采用了两种组合方式，螺钉、螺孔组合分别为钢-钢组合和钢-铝组合，具体材料参数如表1所示[4]。

表1 材料参数

Tab.1 Material Parameter

项目弹性模量/GPa泊松比 结构钢2000.3 铝合金710.33

2.2.2 边界参数设置

为真实反映螺纹的结合方式，将螺纹副的结合方式设置为frictional（摩擦接触）[5]，其当量摩擦系数为0.15，具体边界设置如图4所示。

图4 螺纹边界设置

2.2.3 网格参数设置

综合考虑产品的仿真精度以及对计算资源的需求，采用整体网格划分与螺纹接触面网格细化的网格参数设置策略，具体参数设置如表2所示。

表2 网格参数

Tab.2 Mesh Parameter

项目主网格尺寸/mm接触面网格尺寸/mm 螺钉20.3 螺孔2 连接座50.3

2.2.4 载荷参数设置

对于轴向载荷螺纹连接方式，为确保在轴向载荷作用下连接零件可靠接触，通常需施加大于轴向载荷的预紧力，因此，按照产品的实际使用工况，将螺孔施加固定约束（Fixed Support），在螺钉轴向施加螺纹预紧力（Bolt Pretension）[5]，载荷参数设置如图5所示。

图5 螺纹载荷设置

2.2.5 求解参数设置

为获取每圈旋合螺纹牙所承受的轴向载荷，在螺纹部位添加接触力传感器（Probe）[5]，通过传感器可以获取每圈内、外螺纹在承载情况下相互之间的接触力，该接触力可以反映出每圈螺纹的真实承载情况。接触力施加如图6所示。

图6 螺纹接触力求解设置

2.3 螺纹接触力的统计分析

本文以航天伺服领域中常用的M6、M8、M10 三种螺纹规格作为分析对象，通过有限元仿真分析，分析螺距以及材料差异对螺纹牙承载力分布的影响。结构钢螺钉、螺孔组合以及结构钢螺钉和铝合金螺孔组合的第1～10有效旋合螺纹牙的接触力数据分别如表3和表4所示。

表3 钢-钢组合螺纹牙接触力仿真数据

Tab.3 Simulation Data of Contact Force between Steel and Steel Thread Connection

螺纹规格/mm轴向载荷/N第n圈螺纹接触力/N（n=1，2，…，10） 12345678910 M10×1.560001221909.8670.4513.4399.1322.1258.7223189.4172.8 M10×1.2560001074.1845.7655.1524.6426.2355.7306.4272246.9219.2 M10×16000906.4779.6637.2533.8453.4398.1362.9342.5328.2303.6 M10×0.756000762.6706.8626556.2498.4456.9428.6408.8390.6360 M8×1.254000794.6606.4447.4341.3262.8206.9166.1136.8114.897.4 M8×14000679.6561.3441.9356.1290.7242.5209.5187.8172.3156 M8×0.754000566.1500.9423.9364.1315.1280.8257.8244.8235.9220.5 M6×12400481.7370.8274.9200.7162.9122.997.175.660.246.1 M6×0.752400395.8330.6266.8218.8179.9151.6131.6118.310892.4

表4 钢-铝组合螺纹牙接触力仿真数据

Tab.4 Simulation Data of Contact Force between Steel and Aluminium Thread Connection

螺纹规格/mm轴向载荷/N第n圈螺纹接触力/N（n=2，3，…，11） 234567891011 M10×1.560001049.3833.5642.1519.8429.5367319.8293.3277.3277.2 M10×1.256000933787.4630.1523.1443.6388.7353.9335.3329.8330.3 M10×16000787.2732.7619.1533.3465.6421.3396.5387.9393.2408.1 M10×0.756000633.7660.9609552.6502.8470451.7448.3457.9483.7 M8×1.254000689.5562.9437.1353.6290243.5209.6187174167 M8×14000578.1518.1426.2358.6306.8269245.2233230233.5 M8×0.754000463.3463.5412.5365.4325.5298.7283.6279.8286.1302.3 M6×12400407.9344.2271.8220.6181.4149.7126.7109.698.891.4 M6×0.752400301258.8223.3193.2171.2156.5148.9147.4150.4106.8

对仿真数据进行统计分析，得出如下结论：对于同种材料，不同螺纹规格，螺纹连接的承载力分布与螺距相关，其变化趋势符合下述3次多项式关系，多项式各系数分别如表5和表6所示。

多项式的形式如下：

表5 钢-钢组合多项式系数

Tab.5 Polynomial Coefficient of Steel and Steel

螺距/mmabcd 1.5-3.06×10-47.87×10-3-7.20×10-22.67×10-1 1.25-2.33×10-46.24×10-3-6.04×10-22.43×10-1 1-2.02×10-45.47×10-3-5.37×10-22.28×10-1 0.75-8.3×10-52.64×10-3-3.05×10-21.77×10-1

表6 钢-铝组合多项式系数

Tab.6 Polynomial Coefficient of Steel and Aluminium

螺距/mmabcd 1.5-1.76×10-45.14×10-3-5.14×10-22.21×10-1 1.25-1.27×10-44.04×10-3-4.33×10-22.04×10-1 1-7.41×10-52.93×10-3-3.54×10-21.89×10-1 0.752.29×10-58.39×10-4-1.75×10-21.43×10-1

根据多项式分别计算绘制钢-钢组合和钢-铝组合的螺纹承载力分布曲线，分别如图7和图8所示。

图7 钢螺钉-钢螺孔载荷分布曲线

图8 钢螺钉-铝螺孔载荷分布曲线

分析图7、图8曲线得出如下结论：

a）在内外螺纹均为结构钢的情况下，螺距越大，第1圈螺纹的承载力越大，且第1圈的承载力高于其他圈。当螺距为1.5 mm时，第1圈承载力占螺纹总载荷的20%；当螺距为0.75 mm时，第1圈承载力占螺纹总载荷的15%；

b）在螺距相同的情况下，内螺纹为结构钢的承载力高于铝合金。当螺距为1.5 mm时，其中不锈钢第1圈承载力占螺纹总载荷的20%，铝合金为第1圈承载力占螺纹总载荷的17.5%。

因此，对于内、外螺纹均为结构钢或内、外螺纹分别为铝合金、结构钢的螺纹连接，基于安全性设计的原则，其螺纹旋合圈数为5。

3 结 论

本文采用ANSYS有限元分析对航天伺服系统常用的连接螺纹进行了仿真分析，通过分析旋合螺纹每圈的接触力获得了螺纹牙的承载力分布规律及曲线，为传统螺纹强度设计中的旋合圈数的确定提供了新的解决途径。

[1] 孙训方, 方孝淑, 关来泰. 材料力学[M]. 北京: 高等教育出版社, 2009.

Sun Xunfang, Fang Xiaoshu, Guan Laitai. Mechanics of materials[M]. Beijing: Higher Education Press, 2009.

[2] 成大先. 机械设计手册（第五版）[M]. 北京: 化学工业出版社, 2014.

Cheng Daxian. Mechanical design manual(5th Edition)[M]. Beijing: Chemical Industry Press, 2014.

[3] 濮良贵, 纪名刚. 机械设计[M]. 北京: 高等教育出版社, 2006.

Pu Lianggui, Ji Minggang. Mechanical design[M]. Beijing: Higher Education Press, 2006.

[4] 宋小龙, 安继儒. 新编中外金属材料手册[M]. 北京: 化学工业出版社, 2012.

Song Xiaolong, An Jiru. New manual of Chinese and foreign metal materials[M]. Beijing: Chemical Industry Press, 2012.

[5] 许京荆. ANSYS Workbench 工程实例详解[M]. 北京: 人民邮电出版社, 2015.

Xu Jingjing. ANSYS Workbench details of engineering examples[M]. Beijing: Posts & Telecom Press, 2015.

The Research on Design Technology of Thread Connection Strength Based on Finite Element Analysis

Li Jun-yan, Bao Ting-ping, Hou Peng-fei, Cheng Zhao-yi, Chen An-ping

(Beijing Institute of Precision Mechatronics and Controls, Beijing, 100076)

The strength check of threaded teeth is simulated and analyzed by finite element method. The bearing capacity distribution law of thread connection is obtained by extracting the contact force of threaded teeth, which provides a new way to solve the number of turning circles in traditional thread strength calculation.

finite element analysis; threaded teeth; contact force

TH123+.3

A

1004-7182(2020)02-0078-05

10.7654/j.issn.1004-7182.20200215

李俊岩（1981-），男，高级工程师，主要研究方向为伺服系统。

包婷萍（1978-），女，高级工程师，主要研究方向为伺服控制。

侯鹏飞（1989-），男，工程师，主要研究方向为伺服系统。

成兆义（1978-），男，研究员，主要研究方向为伺服系统。

陈安平（1980-），男，研究员，主要研究方向为伺服系统。

2019-03-11；

2019-10-08