高超声速巡航气动参数/轨迹联合优化与算法比较

王开强，张柏楠，左 光，侯砚泽

高超声速巡航气动参数/轨迹联合优化与算法比较

王开强，张柏楠，左 光，侯砚泽

（北京空间技术研制试验中心，北京，100094）

针对高超声速稳态巡航飞行的气动参数/轨迹联合优化问题，设计了嵌套形式的两级优化器。其中，内层优化器针对巡航轨迹进行优化，优化算法选用序列二次规划算法（Sequential Quadratic Programming，SQP）；外层优化器基于巡航轨迹的优化结果，对气动参数进行优化，分别采用序列二次规划算法、遗传算法（Genetic Algorithm，GA）和基于两者的混合算法进行优化。对整个联合优化问题进行了描述，对嵌套联合优化的方法优势和流程进行了说明。给出了嵌套优化器在内外2层的优化模型，包含设计变量、目标函数和约束条件。最后，进行了多组联合优化仿真，得到了巡航航程随升阻比提高的优化幅度曲线。同时，对不同外层优化算法下的优化全局性、计算效率等进行了对比分析，并结合各方法的优缺点，给出了实际优化问题中优化算法选用的建议。

高超声速稳态巡航；气动参数；巡航轨迹；联合优化；嵌套两级优化

0 引 言

高超声速巡航飞行器具有更快的巡航飞行速度以及更高的巡航高度，有助于低成本地实现可重复的二级入轨以及天地往返飞行，近年来得到了广泛的重视和研究。巡航飞行是整个飞行过程中的重要飞行阶段，扮演很重要的角色。目前，美国X-43高超声速飞行器已实现了马赫数大于7的稳态巡航飞行[1,2]。

目前已有很多关于巡航轨迹优化的研究。Starkey等[3,4]对高超声速乘波体飞行器的巡航轨迹进行了优化，其中应用了差分进化算法和Matlab优化工具箱。Wang等[5]结合采用直接打靶法、第2代直接搜索域法和序列二次规划算法（Sequential Quadratic Programming，SQP），对高超声速稳态巡航轨迹进行了多目标优化。Chen等[6]基于Matlab优化工具箱，分别以每千米的燃油消耗率和总燃油消耗量最小为优化目标，对高超声速乘波体飞行器的稳态巡航、周期性巡航飞行轨迹进行了优化和对比。Kang等[7,8]设计了内外嵌套形式的两级优化器，对高超声速最优周期性巡航轨迹进行了优化。其中内层优化器采用SQP算法，针对巡航攻角的控制变量进行优化；外层优化器采用遗传算法（Genetic Algorithm，GA），对巡航飞行的初值进行优化。

目前已有部分将轨迹、气动相结合的优化研究。Bowcutt[9]基于多学科设计优化方法，开展了吸气式高超声速飞行器航程最大的优化研究，包含气动、轨迹、控制等学科。Tsuchiya等[10]同样将多学科优化方法应用于吸气式高超声速实验飞行器的设计中，建立了外形几何模型、气动及代理模型、轨迹模型等多个学科模型，通过优化得到飞行器的最优外形和相应飞行轨迹。张红文等[11]对高超声速乘波体再入飞行器的外形/轨迹进行了一体化优化，其中首先给出一组离散的乘波体高宽比作为轨迹优化中的静态参数，然后针对每个高宽比取值分别进行轨迹优化，最后从中挑选航程最优的轨迹及相应的乘波体高宽比作为最终优化解。

目前，在巡航轨迹优化研究中，均以固定的气动参数作为输入参数。而在将气动优化、巡航轨迹优化相结合的部分研究中，轨迹的部分参数（例如巡航高度、马赫数）已进行了预先设定，轨迹优化空间有限。或是气动参数采用静态参数的方式进行遍历估计，没有采用优化的手段，其优化效率和优化结果都受到一定限制。本文考虑到巡航飞行在整个任务过程中扮演的重要角色，通过气动参数/轨迹的联合优化，探讨轨迹性能参数随气动参数优化幅度的变化关系，从而得到其对气动参数优化方向的设计期望。由于在气动参数和巡航轨迹两部分均采用优化的方式，因此可以充分挖掘这两部分的优化空间，同时为气动外形设计和巡航轨迹设计提供更具意义的参考。

此外，在优化算法方面，SQP算法在轨迹优化领域应用较多，也出现了GA与SQP算法相结合的轨迹混合优化[8,12]。而气动领域，GA的应用相对较多[13,14]。在一体化优化方面，已有部分将GA与SQP算法相结合的混合优化研究[15]。因此，本文的联合优化中，分别采用SQP算法、GA和基于两者的混合优化算法进行优化。对各方法的特点进行比较分析，并给出实际应用时优化算法选用建议。

1 优化问题与优化策略

1.1 联合优化问题与方法

通常轨迹性能参数的提升希望飞行器的升阻比尽量增大，但是升阻比增加的同时会带来飞行器气动外形设计难度的增加。针对该优化设计矛盾，本文在气动参数方面，设定了一组升阻比增量限值，通过气动参数/轨迹联合优化，探讨巡航轨迹性能优化幅度与升阻比提升幅度的量化关系，为实际有关两者的权衡协调设计提供参考。

联合优化的具体优化思路为：以一定的气动参数为基准参考，确定相应气动参数优化允许的取值范围；然后针对每个升阻比增量限值，在上述气动参数范围内，搜寻令某巡航轨迹性能指标达到最优时的气动参数取值及相应的巡航飞行状态，此时升阻比的增加幅度应不超过设定的增量限值；随后对不同升阻比增量限制下的气动参数和巡航轨迹的优化结果进行对比，得到巡航轨迹性能的优化幅度与升阻比提升幅度的量化关系。整个联合优化实际上是内外嵌套形式的两级优化。外层为气动参数优化，内层为巡航轨迹优化。

对于内层的巡航轨迹优化，采用SQP算法，其处理非线性优化问题时具有很好的搜索效果和效率优势，已广泛应用于轨迹优化领域。对于外层的气动参数优化，本文分别采用SQP算法、GA、和基于GA生成初值后再采用SQP算法的混合优化算法进行优化，对3种方法的优化全局性和计算效率进行对比。整个联合优化流程如图1所示。

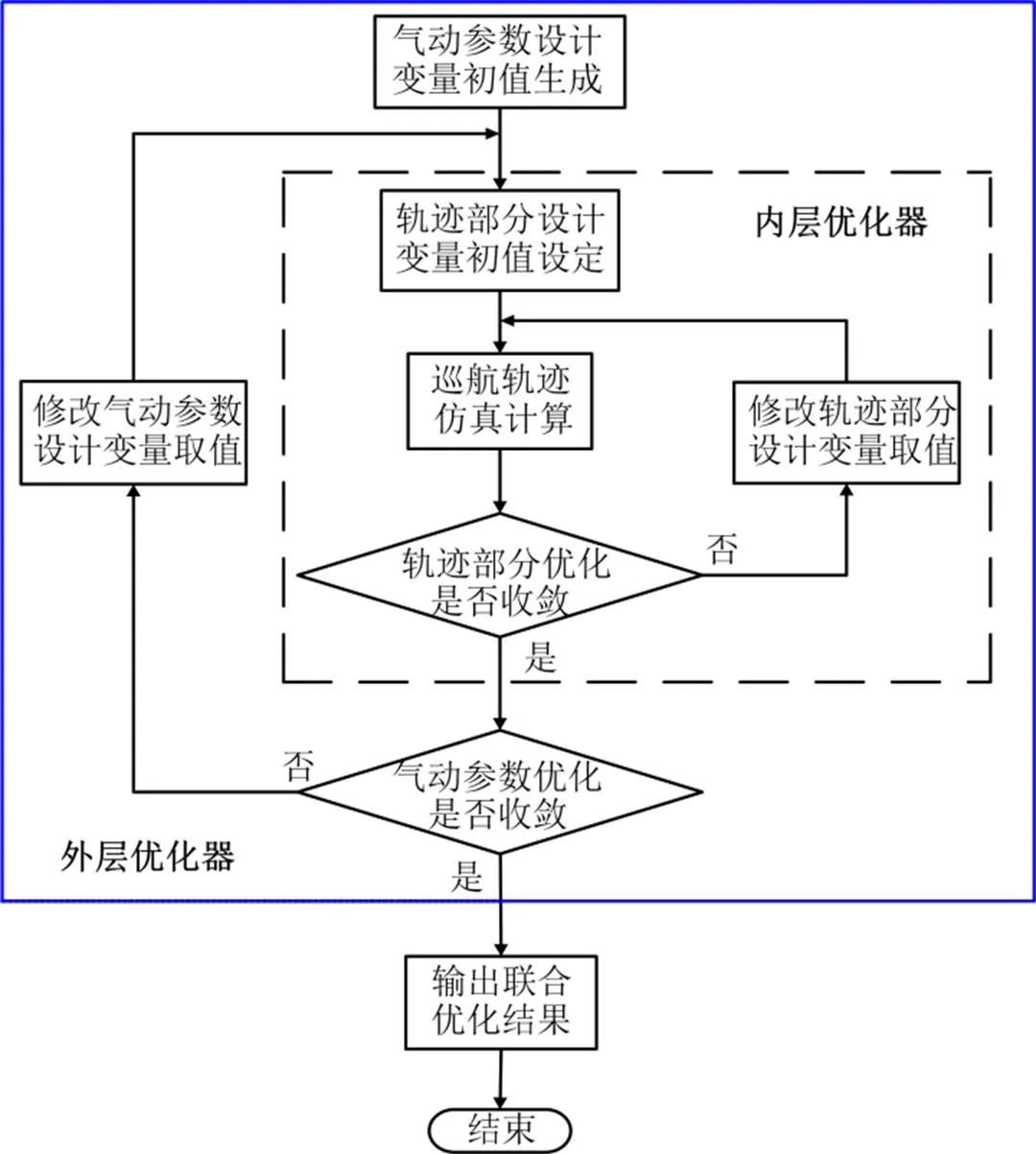
图1 气动参数/轨迹联合优化流程

采用内外嵌套形式的两级联合优化器，可以有针对性的对气动参数、轨迹两类设计变量进行优化，通过内外两级优化器的共同寻优，搜寻联合优化问题的最优解。而联合优化中约束条件的满足，则通过内、外层优化器有针对性的实现。相比于将气动参数、轨迹参数混合在一起的一体化优化形式，该方法的优化规模更小。与此同时，将轨迹优化和气动参数优化分开后交互迭代进行，可以灵活的根据实际需求切换各部分优化时的优化算法选用。例如，本文在外层的气动优化方面，除了采用SQP算法之外，还采用了GA和两者混合的算法，其优化的全局性得到了保证。相比于采用SQP算法的一体化优化，其可以更加充分地搜索和挖掘气动参数的优化空间；而相比于采用GA等进化算法的一体化优化，可以减小轨迹参数部分的优化计算时间。本文联合优化的设计变量、优化目标及约束条件描述如下。

1.1.1 设计变量

本文的联合优化设计变量包括气动参数、巡航轨迹状态参数两部分。

气动参数优化的设计变量为升力系数和阻力系数。对飞行器进行气动参数分析计算时，考虑到CFD计算量巨大，因此通常选取有限的马赫数、攻角进行气动参数分析计算，以表征飞行器的气动特性。例如，美国X-43飞行器就在马赫数为0.3~25的范围内选取了15个特征点，并针对每个马赫数按照5°的步长计算了-10~20°范围内7个攻角下的气动参数[16]。本文采用相同的思路，通过有限的马赫数、攻角特征点的气动参数表征整个飞行器的气动特性。联合优化中，以不同马赫数和攻角下的升力系数L0和阻力系数D0为气动参数基准，取一定百分比的变化范围作为气动参数优化的取值区间。外层优化器根据内层轨迹优化得到的最优马赫数、最优攻角结果，在上述区间内，对相关的马赫数、攻角特征点的气动参数进行优化。

轨迹部分设计变量为巡航初始时刻的高度0cr、马赫数0cr和巡航期间的飞行攻角cr。值得说明的是，巡航飞行期间攻角设为缓慢的线性变化，以保证稳态巡航飞行。

1.1.2 优化目标

本文联合优化部分考虑的优化目标为：巡航飞行航程cr最长。航程的增加有助于扩大飞行器的可达区域覆盖。

1.1.3 约束条件

本文的高超声速巡航为稳态巡航状态，即巡航马赫数基本不变，且航迹角基本为零，由动力学方程可知此时的巡航高度也基本不变。考虑到实际飞行中很难保证马赫数、航迹角的变化量绝对为零，因此需对两者设定一个很小的容许变化范围，如下所示：

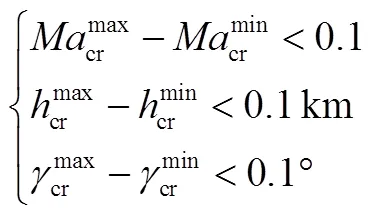
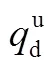
气动参数方面，关于前文提到的升阻比增量，本文采用升阻比增加百分率（简称升阻比增加率）Δ描述，其定义为气动参数优化解的升阻比相比于基准升阻比增加的百分率。关于升阻比增量的限制约束为

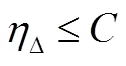
式中为设定的升阻比增加率限值。

1.2 优化模型

本文设计了嵌套形式的两级优化器，求解整个气动参数/轨迹联合优化问题。其中，内层优化器针对轨迹部分的3个设计变量进行优化，优化目标函数与整个联合优化问题的目标相一致，约束条件为稳态巡航关于马赫数、高度、航迹角以及动压的约束。内层优化模型如下：

外层优化器基于巡航轨迹部分的优化结果，针对表1中的8个气动参数进行优化，优化器的目标函数与联合优化问题的优化目标相同，约束条件为升阻比增加率的约束。外层优化模型如下：

式中L，D分别为升力系数和阻力系数。

2 气动参数与巡航轨迹分析模型

本文采用X-43的气动数据和桑格尔的冲压发动机数据，进行气动参数和巡航轨迹的联合优化。考虑到桑格尔发动机的工作马赫数上限为7，工作高度上限为40 km，攻角上限为6°，因此整个高超声速巡航考虑的巡航马赫数范围为6~7，巡航高度范围为20~40 km。巡航攻角方面，本文参考X-43的巡航攻角标称值2.5°[17]，考虑的取值范围为0~3°。

2.1 气动参数模型

依据文献[16]，得到X-43飞行器在马赫数为6~7、攻角为0~5°范围内的升力系数L0和阻力系数D0，如表1所示。其中，原始文献仅有马赫数为6、8时的气动数据，本文对马赫数为6和8的数据进行线性插值，得到马赫数为7的相应气动参数。本文研究的马赫数为6~7、攻角0~3°范围内其余飞行状态下的气动参数均通过原始数据线性插值得到。

以L0、D0为气动参数基准，取±20%的变化范围作为本文气动参数优化变量L和D的取值区间，如表1所示。

表1 气动参数设计变量取值范围

Tab.1 Ranges for Aerodynamic Design Variables

马赫数攻角/(°)CL0CD0CL/CL0CD/CD0 600.01390.0259[0.8, 1.2][0.8, 1.2] 50.13910.0431[0.8, 1.2][0.8, 1.2] 700.01360.0248[0.8, 1.2][0.8, 1.2] 50.13080.0413[0.8, 1.2][0.8, 1.2]

2.2 巡航飞行动力学模型

本文考虑的高超声速稳态巡航飞行过程不进行横侧向的转弯，因此仅考虑飞行器在纵向平面内的运动。另外，为简化分析，巡航轨迹动力学模型中忽略地球自转运动。本文采用的纵向平面动力学方程如下：

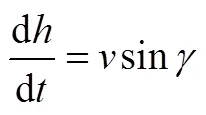
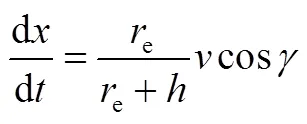
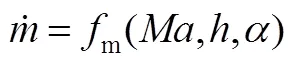
式中t，m分别为根据已知发动机数据，得到的发动机推力和质量秒耗量的线性插值函数关系。

和分别为气动升力和阻力，计算如下：

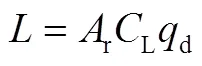
式中r为飞行器的参考面积，本文取r=2 m2；动压d计算如下：

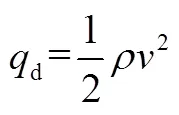
式中为大气密度。

2.3 大气模型

大气模型采用美国SA76模型[6]，此时可根据飞行高度计算得到大气密度和大气温度：

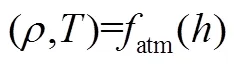
式中atm为SA76模型根据飞行高度计算大气密度、温度的函数关系。此时一定高度上的声速s可由以下公式计算：

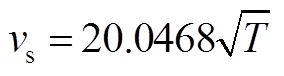
从而进一步计算得到相应高度上的马赫数：

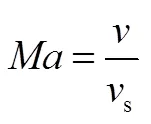
3 优化结果与比较分析

本文按照升阻比增加率Δ分别等于0、10%、20%、30%、40%和50%，采用Matlab R2016a软件进行了上述6组联合优化的仿真。其中，优化算法采用Matlab自带的SQP算法和GA优化算法函数。另外，飞行器空重为1300 kg，燃油质量为100 kg。

3.1 优化结果

6组优化结果中，最优巡航马赫数均为7，因此气动参数设计变量中，仅马赫数等于7的4个气动参数得到了有效优化。本节限于篇幅，不罗列所有6组的详细优化结果。仅列出能体现3种算法特性的代表性算例结果。

a）Δ=0。

采用3种优化算法得到的优化解如表2所示，其中将优化得到的升力系数L和阻力系数D与原X-43飞行器的相应系数L0和D0的比值在表中予以展现，以便于更清晰地分析优化解相对于原数据的变化幅度。可以看出，本算例中，SQP算法得到的优化解的巡航航程最优，且其计算时间很短，这与SQP算法优化初值的设定接近于最优解有关；而GA则得到了最优航程附近的设计解；混合算法则由于SQP算法在GA优化生成的初值附近没有搜寻至更优的设计解，因此得到的优化解与GA相同，未能得到比SQP算法更好的结果。优化结果与比较如表2所示。

表2 优化结果与比较（ηΔ=0）

Tab.2 Optimization Result and Comparison (ηΔ=0)

参数外层优化器 SQP算法GA算法GA+SQP 联合优化目标巡航飞行航程xcr/km278271271 外层优化CL/CL0(Ma=7)0°攻角1.20.880.88 5°攻角1.21.121.12 CD/CD0(Ma=7)0°攻角1.20.880.88 5°攻角1.21.121.12 内层优化初始巡航高度h0cr/km27.326.826.8 初始巡航马赫数Ma0cr777 最大巡航攻角/(°)333 最小巡航攻角/(°)2.862.732.71 总巡航时间/s134130130 优化用时/min2239533995

b）Δ=10%。

3种优化算法得到的优化解如表3所示。

表3 优化结果与比较（ηΔ=10%）

Tab.3 Optimization Result and Comparison (ηΔ=10%)

参数外层优化器 SQP算法GA算法GA+SQP 联合优化目标巡航飞行航程xcr/km282297297 外层优化CL/CL0(Ma=7)0°攻角1.190.900.90 5°攻角1.191.191.19 CD/CD0(Ma=7)0°攻角1.090.850.85 5°攻角1.081.081.08 内层优化初始巡航高度h0cr/km27.327.127.1 初始巡航马赫数Ma0cr777 最大巡航攻角/(°)333 最小巡航攻角/(°)2.752.752.72 总巡航时间/s135142142 优化用时/min18444774606

本例中，SQP算法得到了局部最优解，体现了其全局搜索能力相对较弱的劣势。而GA和混合算法均优化得到了更好的优化解，体现出了GA很好的全局性。其中，混合算法则由于SQP算法在GA的初值附近没有搜寻出更好的设计解，因此得到的结果与GA相同。同样的上述算法特性也体现在Δ=20%的算例结果中，其优化结果见表6，本文不再单独赘述。

c）Δ=30%。

3种优化算法得到的优化解如表4所示。

表4 优化结果与比较（ηΔ=30%）

Tab.4 Optimization Result and Comparison (ηΔ=30%)

参数外层优化器 SQP算法GA算法GA+SQP 联合优化目标巡航飞行航程xcr/km333339344 外层优化 CL/CL0(Ma=7)0°攻角1.181.061.04 5°攻角1.181.21.2 CD/CD0(Ma=7)0°攻角0.910.850.8 5°攻角0.910.920.93 内层优化初始巡航高度h0cr/km27.227.227.2 初始巡航马赫数Ma0cr777 最大巡航攻角/(°)333 最小巡航攻角/(°)2.732.722.73 总巡航时间/s160162165 优化用时/min6344204494

其中，SQP算法优化得到了某局部最优解，GA则相对改善了优化解的全局性，混合算法则很好地综合了GA的全局性好和SQP算法局部搜索能力强的优点，得到了更优的优化解。同样的上述算法特性也体现在Δ=40%的结果中。其优化结果如表6所示。

d）Δ=50%。

基于3种优化算法得到的优化解如表5所示。其中，SQP算法和混合算法均优化得到了全局性很好的优化解，而GA则体现了其局部优化能力弱的劣势。优化结果与比较见表5。

表5 优化结果与比较（ηΔ=50%）

Tab.5 Optimization Result and Comparison (ηΔ=50%)

参数外层优化器 SQP算法GA算法GA+SQP 联合优化目标巡航飞行航程xcr/km385380385 外层优化 CL/CL0(Ma=7)0°攻角1.21.161.2 5°攻角1.21.21.2 CD/CD0(Ma=7)0°攻角0.80.810.8 5°攻角0.80.810.8

续表5

参数外层优化器 SQP算法GA算法GA+SQP 内层优化初始巡航高度h0cr/km27.327.327.3 初始巡航马赫数Ma0cr777 最大巡航攻角/(°)333 最小巡航攻角/(°)2.742.742.74 总巡航时间/s184182184 优化用时/min1556635678

3.2 比较与分析

将不同升阻比增加率下的气动参数/轨迹联合优化解及优化耗时汇总对比如表6所示。其中，定义基于X-43原气动参数的航程最优巡航轨迹为基准解，定义优化解的巡航航程相对于基准解航程提升的百分率为巡航航程增加率。其随升阻比增加率的变化如图2所示。将基准解的巡航轨迹与部分升阻比参数下的优化巡航轨迹进行了对比，如图3所示。可以看出3条巡航轨迹中巡航高度变化很小，满足本文的稳态巡航要求。

分析表2~5和图2可知，各最优解对于巡航飞行航程的改进较为明显，相比于基准解的航程提升幅度最大可达50%。巡航航程增加幅度随升阻比增加率的变化基本呈现线性关系。实际设计中，需结合巡航轨迹设计需求和气动外形设计的技术难度进行权衡设计。

图2 巡航航程随升阻比增加的关系曲线

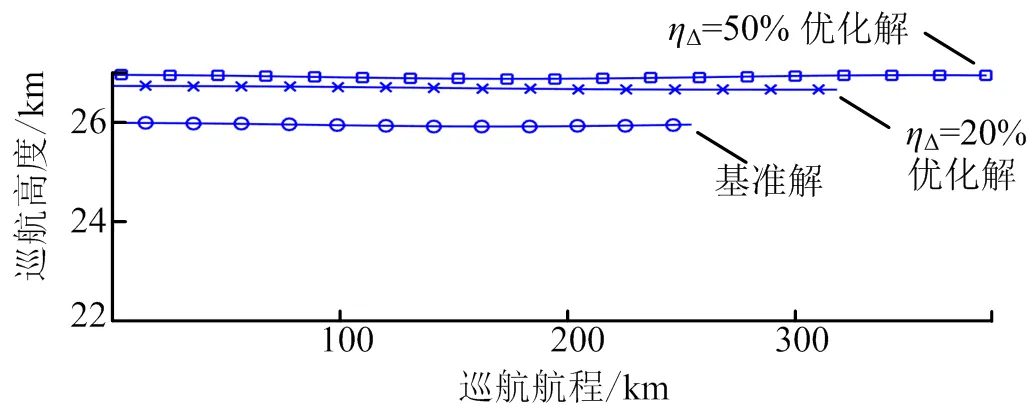
图3 巡航轨迹

表6 优化结果汇总与对比

Tab.6 Optimization Result and Comparison

参数基准解优化解 ηΔ=0ηΔ=10%ηΔ=20%ηΔ=30%ηΔ=40%ηΔ=50% 最优巡航航程xcr/km256278297320344365385 巡航航程增加率08.6%16%25%34.3%42.6%50.4% 优化解的巡航航程与最优航程之比SQP—100%94.9%95%96.8%98.1%100% GA—97.5%100%100%98.5%99.5%98.7% GA+SQP—97.5%100%100%100%100%100% 优化时间与混合算法耗时之比SQP—0.55%4%2.1%1.4%4.2%0.26% GA—98.9%97.2%98.5%98.4%95.4%99.7%

从表6可以看出，外层气动参数优化基于SQP算法得到的优化解大致在全局最优解附近，其局部最优解相比于目标函数全局最优值的削减幅度约5%，但是其计算效率极高，计算耗时通常在GA算法以及混合算法的1%量级。当初值设置非常理想时，SQP算法可以直接搜寻到全局最优解，此时的计算耗时进一步缩短，仅为GA和混合算法的0.1%量级。而当外层气动参数优化采用GA时，其优化解的全局性相较于SQP算法得到了一定改善，相比于目标函数最优值的削减幅度约为2.5%，但其计算效率很低。而外层采用GA+SQP的混合优化时，基本可以确保得到全局性的最优解，但是其采用了GA作为后一步的SQP算法优化的初值生成器，因此计算效率仍然很低。

4 结 论

本文针对高超声速巡航飞行的气动参数/轨迹联合优化问题，设计了嵌套形式的两级优化器，建立了各级优化模型。其中，内层优化器基于SQP算法针对巡航轨迹进行优化；外层优化器基于巡航轨迹的优化结果，分别采用SQP算法、GA算法和GA+SQP的混合算法进行气动参数优化。得到的结论如下：

a）本文得到的各组联合优化解的巡航航程均优于基准解，提升幅度最大可达50%。在每组优化中，外层优化器搜索得到了升阻比提升幅度一定时的最优升力系数和阻力系数取值。因此，本文关于嵌套形式两级优化器的设计、优化模型的定义以及相关优化算法的选用合理有效，可有针对性地完成气动参数部分和巡航轨迹部分的优化，从而实现整个联合优化问题的有效求解。

b）优化算法方面，SQP算法易得到局部优化解，但其计算效率很高。当初值给的非常合理时，SQP算法可以得到全局性的最优解，此时计算耗时可进一步缩短。遗传算法GA得到的优化解在全局性方面得到了改善，但其计算效率很低。而GA+SQP的混合优化算法基本可以确保得到全局最优解，但其计算耗时仍然很长。实际优化应用中，需根据优化解的全局性要求和容许的设计时间，选用合适的优化算法。

[1] Mcclinton C R, Rausch V L, Nguyen L T, Sitz J R. Preliminary X-43 flight test results[J]. Acta Astronautica, 2005, 57(2): 266-276.

[2] Baumann E. X-43A flight controls[R]. NASA- 20060047627, 2006.

[3] Starkey R, Rankins F, Pines D. Coupled waverider/trajectory optimization for hypersonic cruise[R]. AIAA 2005-530, 2005.

[4] Starkey R, Rankins F, Pines D. Effects of hypersonic cruise trajectory optimization coupled with airbreathing vehicle design[R]. AIAA 2006-337, 2006.

[5] Wang K Q, Zhang B N, Hou Y Z. Multiobjective optimization of steady-state cruise trajectory for a hypersonic vehicle[C]. Beijing: In Proceedings of 3rd IEEE International Conference on Control Science and Systems Engineering (ICCSSE), 130-135, 2017.

[6] Chen R H, et al. Optimization and implementation of periodic cruise for a hypersonic vehicle[J]. Journal of Guidance, Control and Dynamics, 2006, 29(5): 1032-1040.

[7] Kang B N, Spencer D B, Tang S, Jordan D. Study of optimal periodic cruise trajectories via tradespace visualization[R]. AIAA 2009-6285, 2009.

[8] Kang B N, Spencer D B, Tang S, Jordan D. Optimal periodic cruise trajectories via a two-level optimization method[J]. Journal of Spacecraft and Rockets, 2010, 47(4): 597-613.

[9] Bowcutt K G. Multidisciplinary optimization of airbreathing hypersonic vehicles[J]. Journal of Propulsion and Power, 2001, 17(6): 1184-1190.

[10] Tsuchiya T, Takenaka Y, Taguchi H. Multidisciplinary design optimization for hypersonic experimental vehicle[J]. AIAA Journal, 2007, 45(7): 1655-1662.

[11] 张红文, 张科南, 陈万春. 带静态参数的高超声速飞行器轨迹优化算法[J]. 北京航空航天大学学报, 2014 (2): 141-147.

Zhang Hongwen, Zhang Kenan, Chen Wanchun. Indirect method for trajectory optimization of hypersonic vehicle with static parameters[J]. Journal of Beijing University of Aeronautics and Astronautics, 2014(2): 141-147.

[12] 张鼎逆, 刘毅. 基于改进遗传算法和序列二次规划的再入轨迹优化[J]. 浙江大学学报（工学版）, 2014, 48(1): 161-167.

Zhang Dingni, Liu Yi. Reentry trajectory optimization based on improved genetic algorithm and sequential quadratic programming[J]. Journal of Zhejiang University (Engineering Science), 2014, 48(1): 161-167.

[13] 车竞, 唐硕, 何开锋. 高超声速巡航飞行器机身多目标优化设计[J]. 实验流体力学, 2008, 22(1): 55-60.

Che Jing, Tang S, He Kaifeng. Multi-objective optimization design of airframe for hypersonic cruise vehicle[J]. Journal of Experiments in Fluid Mechanics, 2008, 22(1): 55-60.

[14] 刘济民, 侯志强, 宋贵宝, 朱旭程. 高超声速巡航导弹乘波构型优化设计与性能分析[J]. 空气动力学学报, 2011, 29(1): 118-123.

Liu Jimin, Hou Zhiqiang, Song Guibao, Zhu Xucheng. Optimization design and aerodynamic characteristic analysis of waverider based hypersonic cruise missile configuration[J]. Acta Aeodynamica Sinica, 2011, 29(1): 118-123.

[15] 胡凡, 杨希祥, 江振宇, 张为华. 固体运载火箭轨迹/总体参数一体化优化设计研究[J]. 固体火箭技术, 2010, 33(6): 599-602, 610

Hu Fan, Yang Xixiang, Jiang Zhenyu, Zhang Weihua. Optimization design and aerodynamic characteristic analysis of waverider based hypersonic cruise missile configuration[J]. Acta Aeodynamica Sinica, 2011, 29(1): 118-123.

[16] Brock M A. Performance study of Two-Stage-To-Orbit reusable launch vehicle propulsion alternatives[D]. Ohio: Air Force Institute of Technology, 2004.

[17] Bahm C, Baumann E, Martin J, et al. The X-43A Hyper-X Mach 7 flight 2 guidance, navigation, and control overview and flight test results[R]. AIAA 2005-3275, 2005.

Integrated Optimization of Aerodynamic Parameters and Trajectory for Hypersonic Cruise Flight and Algorithm Comparison

Wang Kai-qiang, Zhang Bai-nan, Zuo Guang, Hou Yan-ze

(Institute of Manned Space System Engineering, China Academy of Space Technology, Beijing, 100094)

To solve the integrated optimization problem of aerodynamic parameters and trajectory for hypersonic steady-state cruise, a nested two-level optimizer is designed. The inner loop is for cruise trajectory optimization using Sequential Quadratic Programming (SQP) algorithm, while the outer one is to optimize the aerodynamic parameters based on the trajectory optimization result with the use of SQP, Genetic Algorithm (GA) and the hybrid of the two algorithms, respectively. The whole integrated optimization problem is described, and advantages as well as the procedure of the nested integrated optimization are illustrated. Then, the optimization models on both levels of the nested optimizer are given, including the design variables, objective functions and constraints. Finally, a group of optimizations are implemented, and the variation curve between the increase percentage in the cruise range and the lift-drag ratio improvement is acquired. In addition, the three algorithms utilized in the outer loop optimization are compared in terms of the globality of the optimal solution and the optimization efficiency. According to the advantages and disadvantages of the algorithms, some suggestions are given for the optimization algorithm choosing in the practical problems.

hypersonic steady-state cruise; aerodynamic parameters; cruise trajectory; integrated optimization; nested two-level optimization

V421.1

A

1004-7182(2020)02-0016-08

10.7654/j.issn.1004-7182.20200204

王开强（1988-），男，博士，工程师，主要研究方向为飞行器总体参数设计优化、飞行力学与轨迹优化。

张柏楠（1962-），男，研究员，主要研究方向为飞行器系统总体设计。

左 光（1971-），男，研究员，主要研究方向为飞行器总体与气动设计。

侯砚泽（1982-），男，博士，高级工程师，主要研究方向为飞行器总体与控制设计。

2018-01-19；

2019-05-08

国家自然科学基金（61403028）