亚轨道飞行器返回轨迹设计方法

韩 璐，石宝兰，毕永涛，黄 宇

亚轨道飞行器返回轨迹设计方法

韩 璐，石宝兰，毕永涛，黄 宇

（北京宇航系统工程研究所，北京，100076）

针对亚轨道飞行器返回轨迹设计难点以及当前已有方法和模型的不足，提出了一种亚轨道飞行器返回轨迹设计方法。将返回轨迹分为初始返回段和机动转弯段，在机动转弯过程引入航向角偏差参数，并根据该参数标志的转弯终点对倾侧角进行迭代求解，能够有效处理亚轨道飞行器返回过程大范围机动转弯问题以及返回过程的各类约束，并通过算例验证了方法的可行性。设计方法符合亚轨道飞行器返回轨迹特点，能够满足设计要求。

亚轨道飞行器；返回轨迹；设计方法

0 引 言

近年来，为了更加便捷地探索和利用亚轨道空间，各国对可重复使用亚轨道飞行器进行了不懈研究[1~4]。为了降低使用和维护成本，要求亚轨道飞行器在亚轨道完成空间任务后，能依靠自身能量返回指定着陆场。

对于升力式飞行器的再入轨迹设计方法，航天飞机再入采用了基于阻力加速度的标称轨迹法[5,6]。陆平在拟平衡滑翔假设条件下，提出一种将再入过程不等式约束转化为对倾侧角幅值约束的在线轨迹生成方法[7]。Mease提出了一种降阶模型的在线阻力加速度参考剖面生成方法[8,9]，并将传统二维纵向制导律推广到三维。

然而，亚轨道飞行器返回轨迹与当前已有升力式再入航天器存在较大的差别：a）当前已有升力式再入航天器再入初始能量大且能量相对固定（从绕地轨道返回），航程容易满足，横向机动距离需求小。而亚轨道飞行器返回初始状态（初始能量）由所执行的具体任务决定；b）亚轨道飞行器在完成任务后返回过程中，很可能需要在大范围三维空间进行转弯机动，难以对剩余航程进行准确预估，而文献[5]~[9]中的方法均需对飞行器剩余航程进行预先估计，难以直接应用。

因此，当前已有的再入模型均无法完全适用于亚轨道飞行器返回轨迹设计。本文根据亚轨道飞行器返回轨迹特点，提出适用于亚轨道飞行器返回轨迹的设计方法，并通过典型算例，对方法的可行性进行验证。

1 数学模型

1.1 问题描述

亚轨道飞行器完成预定任务后返回指定的着陆场，其返回剖面示意如图1所示。

图1 亚轨道飞行器返回剖面

亚轨道飞行器完成预定任务后动压较小，需在适当降低飞行高度、提升动压后进行机动转弯。为了返回指定的着陆点，需使得转弯结束后飞行器的飞行方向满足预定要求。同时，返回过程中飞行器必须满足力热环境约束。为保证飞行器最终成功降落于指定着陆场，返回过程中飞行器抵达相距着陆点一定距离的某个界面（末端能量管理界面）时，飞行状态需满足一定条件，从末端能量管理界面至飞行器最终着陆之间的飞行过程不在本文研究范围内。

1.2 动力学模型

亚轨道飞行器无动力返回，假设返回过程中侧滑角为零，返回段动力学方程为

1.3 约束条件

亚轨道飞行器返回过程主要约束条件包括动压、法向过载和驻点热流约束：

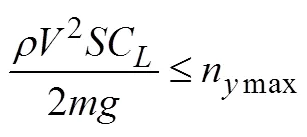
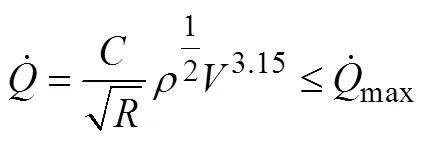
亚轨道飞行器抵达末端能量管理界面时的飞行状态需满足一定条件，主要包括飞行高度和飞行速度：

2 返回轨迹设计方法

根据亚轨道飞行器返回过程特点，将返回轨迹划分为初始返回段和机动转弯段，并分别采用不同的轨迹设计方法。

2.1 初始返回段

亚轨道飞行器在转弯过程中按照拟平衡滑翔条件（Quasi-equilibrium Glide Condition，QEGC）飞行，因此需使飞行器在初始返回段结束时平滑过渡至平衡滑翔条件。

为避免同时设计攻角和倾侧角所带来的困难，采用预先设计确定的攻角剖面，并采用常值倾侧角，倾侧角方向指向飞行器转弯方向。计算倾侧角时，可使倾侧角从某值起始，计算动力学方程式（1），并以式（6）为条件判断初始返回段终点（飞行器处于预先确定的初始返回段和机动转弯段交班速度时的飞行状态）是否满足拟平衡滑翔条件。如果满足拟平衡滑翔条件则转入转弯段；如果不能满足，则对当前倾侧角增加（或减小）某步长值，并重新计算式（1）和检验式（6），直至满足拟平衡滑翔条件。

2.2 机动转弯段

在文献[5]~[9]中，基于飞行器纵向剩余航程预估，对倾侧角剖面进行求解。但亚轨道飞行器初始能量随具体投送任务的不同而不同，因此其返回轨迹形状不规则，且为返回至指定着陆场某些情况下转弯过程飞行方向变化较大，这使得亚轨道飞行器剩余航程的估算十分困难，采用传统方法估算剩余航程结果与实际差别较大，当前已有模型不能完全适用于亚轨道飞行器返回段轨迹设计。

机动转弯段轨迹设计同样采用预先设计确定的攻角剖面，转弯过程中按照拟平衡滑翔条件飞行，满足以下条件：

在转弯过程中，飞行器速度单调递减，且初始和终端速度可根据初始转弯段和末端能量管理界面约束条件明确，因此将式（1）转换成以速度为积分变量的形式：

在转弯过程中，倾侧角取值如下：

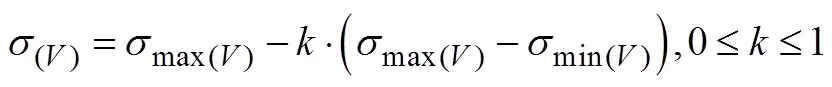
3 算例与分析

某亚轨道飞行器返回初始条件为：初始质量50 t，高度60 km，速度为=14，距发射场纵向距离3250 km，横向距离0 km，弹道倾角5°，弹道偏角0°。飞行器按要求降落于指定着陆场，要求飞行器抵达末端能量管理界面某点（高度30 km，与发射点纵向距离4000 km，横向距离0 km）时，飞行速度750 m/s。飞行器返回轨迹计算结果如图2~6所示。

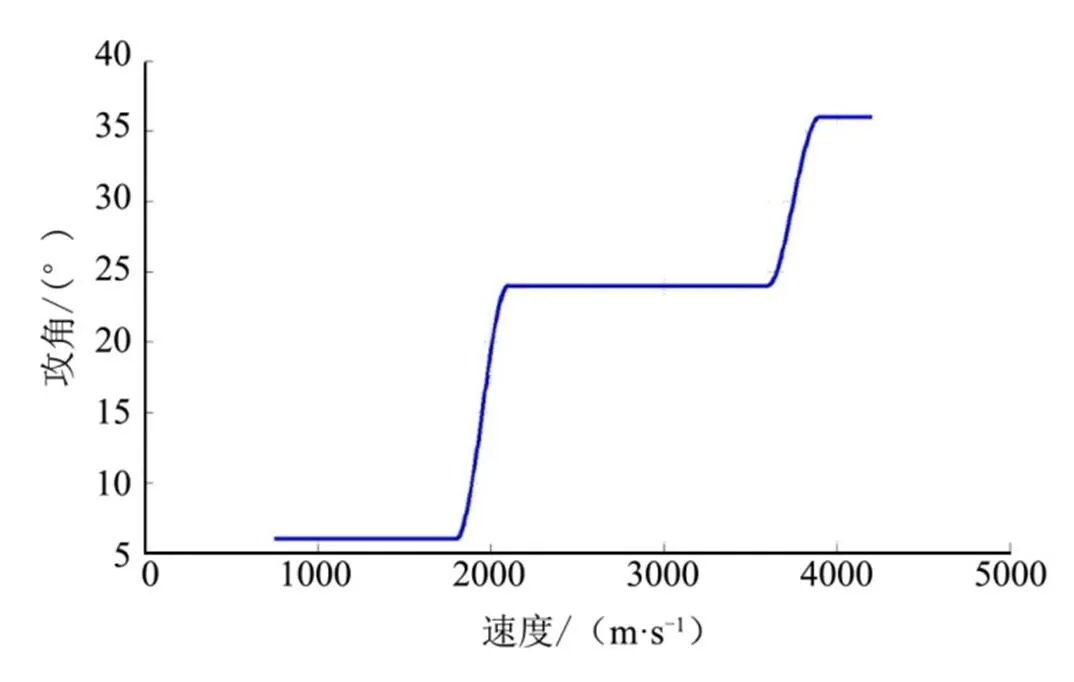
图2 攻角曲线

图3 倾侧角曲线

图4 纵程-高度曲线

图5 纵程-侧向距离曲线

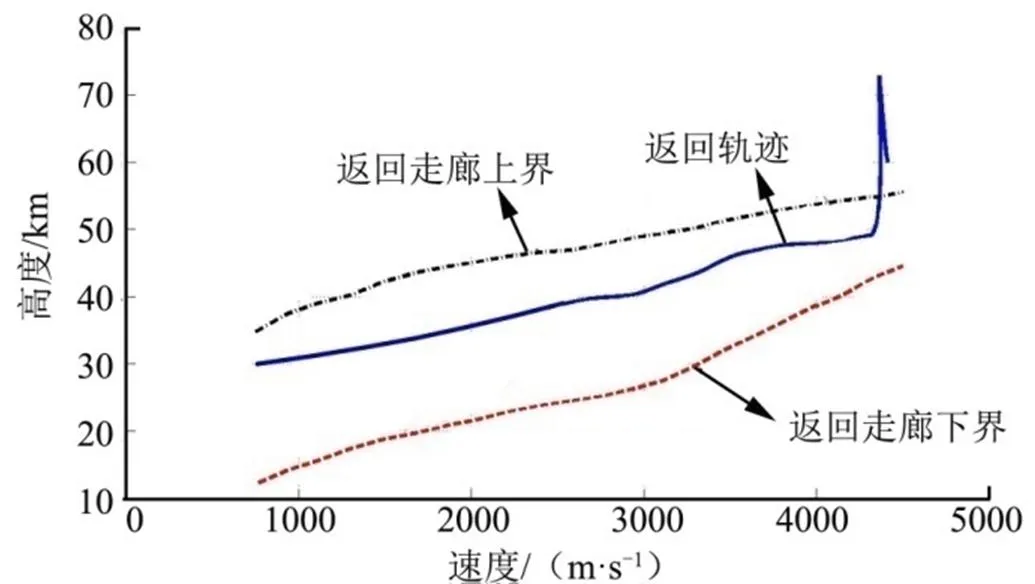
图6 速度-高度曲线

由图5可知，如果采用传统方法预估剩余航程，则剩余航程约750 km，由于剩余航程过短，无法迭代收敛至正确结果。

应用本文方法和模型，算例中，飞行器在执行完预定任务后，初始返回段倾侧角为50°，在高度约49 km处满足拟平衡滑翔条件并进入转弯段，此时速度为=13，转弯段结束时刻航向角偏差约0.5°。当速度为750 m/s时，飞行器高度约30 km，满足终端约束条件。由图6可知，飞行器在返回全程满足所有约束条件。应用本文模型，飞行器实际飞行距离约2100 km。

4 结 论

本文根据亚轨道飞行器返回轨迹特点和返回过程存在的特殊问题，建立了适应于亚轨道飞行器返回轨迹设计的方法和模型，并通过典型算例，对方法和模型的可行性进行了验证。经研究得出如下结论：

a）亚轨道飞行器完成预定任务后返回，需在大范围三维空间进行转弯机动，且返回初始条件随所执行任务的不同而存在较大的变化范围，难以对剩余航程进行准确预估，当前已有方法和模型无法直接应用；

b）方法基于亚轨道飞行器返回轨迹特点，能满足亚轨道飞行器返回轨迹生成要求以及各类约束条件；

c）方法以及所建立轨迹设计模型能够推广应用于亚轨道有动力飞行器返回轨迹设计，适用范围广。

[1] 陈宏, 何国强. RBCC和TBCC组合发动机在RLV上的应用[J]. 火箭推进, 2008, 34(3): 39-43.

Chen Hong, He Guoqiang. Application of RBCC and TBCC engines to RLVs[J]. Journal of Rocket Propulsion, 2008, 34(3): 39-43.

[2] 崔乃刚, 等. 垂直起降可重复使用运载器发展现状与关键技术分析[J]. 宇航总体技术, 2018, 2(2): 27-42.

Cui Naigang, et al. Development and key technologies of vertical takeoff vertical landing reusable launch vehicle[J]. Astronautical Systems Engineering Technology, 2018, 2(2): 27-42.

[3] 龚春林, 等. 适应于RBCC运载器的轨迹优化建模研究[J]. 宇航学报,2013, 34(12): 1592-1598.

Gong Chunlin, et al. Research on modeling of trajectory optimization for RBCC-powered RLV[J]. Journal of Astronautics, 2013, 34(12): 1592-1598.

[4] 龚春林, 韩璐. RBCC可重复使用运载器上升段轨迹优化设计[J]. 固体火箭技术, 2012, 35(3): 290-295.

Gong Chunlin, Han Lu. Optimization of ascent trajectory for RBCC-powered RLV[J]. Journal of Solid Rocket Technology, 2012, 35(3): 290-295.

[5] Harpold J C, Graves C A Jr. Shuttle entry guidance[J]. Journal of the Astronautical Sciences, 1979, 27(3): 239-268.

[6] 赵汉元. 飞行器再入动力学和制导[M]. 长沙: 国防科技大学出版社,1997.

Zhao Hanyuan. Dynamics and guidance for reentry vehicles[M]. Changsha: National University of Defense Technology Press, 1997.

[7] Shen Z J, Lu P. Onboard generation of three-dimensional constrained entry trajectories[J]. Journal of Guidance, Control, and Dynamics, 2003, 26(1): 111-121.

[8] Mease K D. Reduced-order entry trajectory planning for acceleration guidance[J]. Journal of Guidance, Control and Dynamics, 2002, 25(2): 257-266.

[9] Mease K D. Design and evaluation of an acceleration guidance algorithm for entry[J]. Journal of Spacecraft and Rockets, 2004, 41(6): 986-996.

Flyback Trajectory Design Method for Suborbital RLVs

Han Lu, Shi Bao-lan, Bi Yong-tao, Huang Yu

(Beijing Institute of Aerospace Systems Engineering, Beijing, 100076)

In order to solve the design difficulty of the flyback trajectory of the suborbital RLVs(Reusable Launch Vehicle) and the shortcomings of the existing methods and models, a new flyback trajectory design method for Suborbital RLVs is studied. The flyback trajectory is divided into an initial return segment and a maneuvering turn segment, the angular deviation of azimuth is imposed during maneuvering，and the bank angle is iteratively calculated based on the turning end marked by this parameter to deal with large-scale maneuvering problems during the return process of suborbital RLVs, and all the constraints are satisfied. The feasibility of the method is verified by a numerical example. The method accords with the characteristics of flyback trajectory and satisfies the mission requirements.

suborbital RLVs; flyback trajectory; design method

V475.9

A

1004-7182(2020)02-0007-04

10.7654/j.issn.1004-7182.20200202

韩 璐（1989-），男，工程师，主要研究方向为飞行器总体设计。

石宝兰（1988-），女，工程师，主要研究方向为飞行器总体设计。

毕永涛（1982-），男，高级工程师，主要研究方向为飞行器总体设计。

黄 宇（1984-），男，高级工程师，主要研究方向为飞行器总体设计。

2019-04-11；

2019-07-02