惯性稳定平台的扰动观测器/不完全微分PID复合控制

钟婧佳，杨功流，王 汀，于 沛

惯性稳定平台的扰动观测器/不完全微分PID复合控制

钟婧佳，杨功流，王 汀，于 沛

（北京航空航天大学仪器科学与光电工程学院，北京，100191）

为提高惯性稳定平台控制系统的稳态性能，提出了一种扰动观测器与不完全微分PID相结合的复合控制算法。利用扰动观测器将控制系统中存在的外部扰动观测出来并补偿到原系统中，在增强系统扰动抑制能力、提高鲁棒性的同时，提高系统稳定精度。仿真结果表明：扰动观测器/不完全微分PID复合控制算法可显著改善惯性稳定平台的稳态性能，对比于常规PID校正方法，复合控制方法不仅提高了系统的响应速度，而且显著提高系统的扰动抑制能力，提高稳定精度。

惯性稳定平台；扰动观测器；不完全微分PID；扰动抑制

0 引 言

惯性稳定平台是平台式惯导系统的重要组成部分，可以为惯性测量装置提供稳定的工作环境和测量基准，并广泛应用于航天飞行器、火箭、导弹、潜艇等众多领域中[1~4]。其中稳定平台的精度将直接影响导航、制导的精度，其不仅取决于惯性仪表的测量精度，还取决于平台稳定回路的性能[5~7]。稳定回路是通过克服作用在框架轴上的干扰力矩等外界干扰而维持平台稳定的，因此，如何有效克服外界干扰是稳定回路算法设计的研究重点。

随着稳定回路数字化控制方案的不断发展，经典PID校正和超前滞后校正控制方法已经趋于成熟，但仍存在干扰抑制能力不足的问题[8,9]。很多学者把现代控制理论应用到平台稳定回路控制系统的设计中进行仿真分析，中科院数学与系统科学研究院系统科学所的宋金来模拟仿真了二阶自抗扰控制（ADRC）下稳定回路的相应特性。目前，其算法对于二阶系统的应用较为成熟[10]。针对提高系统鲁棒性问题，北京控制仪器研究所的魏宗康博士进行了平台稳定回路的∞鲁棒控制设计研究，经仿真取得了较好的结果[11]。中航工业第六一三研究所的王合龙等人，提出了采用变结构控制对陀螺稳定平台进行伺服控制的方法，一定程度地增强了系统的鲁棒性[12]。针对抑制系统外部扰动的问题，长春光机所的朱明超等人[13]提出了一种自适应前馈控制方法来提高惯性稳定平台控制的指令跟踪性能。目前稳定回路中现代控制方法多数还处于实验室仿真阶段，在工程中应用较少[14]。

本文首先根据实际平台稳定回路的结构及工作原理对控制系统进行建模及分析，并对比分析了经典PID校正、不完全微分PID校正在稳定回路中的仿真效果，总结不完全微分PID的优势及仍然存在的问题。接着根据实际平台惯导系统在不完全微分PID的基础上设计了扰动观测器，以实现高阶系统的复合控制，旨在减小平台稳定过程中外界扰动对稳定回路的影响，提高鲁棒性。最后通过仿真实验验证，证明本文控制方法的可行性。

1 惯性平台稳定回路原理分析

1.1 基本工作原理及模型建立

本文以单自由度积分陀螺仪构成的平台稳定回路为研究对象，对其基本工作原理及控制算法展开了研究，旨在提高系统的动态性能和稳态性能。平台稳定回路的工作原理可以理解为一个伺服控制系统，作用在框架轴上的干扰力矩使平台发生偏转产生角速度，并被陀螺仪敏感进而发生进动，产生的角度偏差通过一系列电路最终转换为控制电信号控制力矩电机输出，从而产生与干扰力矩大小相等方向相反的平衡力矩，使平台停止转动而稳定在惯性空间中[15]。平台系统的3条稳定回路的结构组成基本相同，本文主要对台体轴稳定回路进行了建模、仿真与实验，其控制回路原理框图如图1所示。

图1 平台稳定回路原理框图

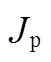
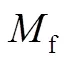
1.2 未校正系统稳定性分析

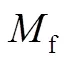
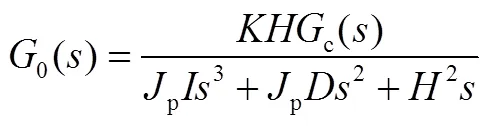
为便于选取校正网络所需环节，这里取，即对未校正系统进行稳定性分析，则可得稳定回路未校正时系统开环幅频特性如图2所示。

由图2可知，未校正网络系统的相角裕度及幅值裕度都不满足系统稳定的条件，因此需引入校正控制网络以提高系统的稳定性，改善系统动态及稳态性能。根据线性系统的校正原理可知，该校正网络至少需引入微分环节提高相角裕度，为消除静差还需要引入积分环节，再通过与比例环节相配合调整截止频率达到期望的响应输出[16]。因此，采用PID控制可以简单方便地对系统进行校正，本文后续章节将对经典PID控制进行分析并做出合理的改进以适应实际需要。

2 不完全微分PID与PID控制

2.1 不完全微分PID与PID的原理分析

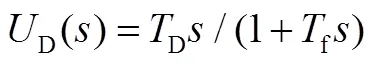
对不完全微分环节进行离散化递推处理，可得：

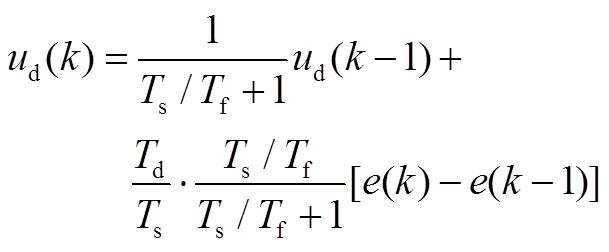
当微分环节的输入设置为阶跃函数时，其阶跃响应在各个采样周期内都有输出，而不是集中在第1个采样周期内，其在各个采样周期的输出可表示为

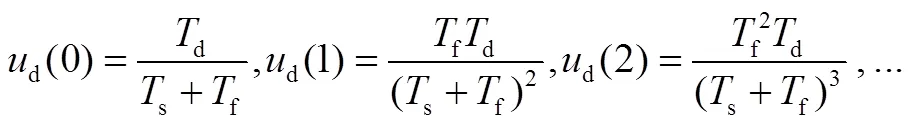
可以看出，加入惯性环节的不完全微分控制可以拉长微分作用时间，削弱微分在第1采样周期内的作用强度，这有助于抑制噪声干扰并加快系统响应速度。二者在各采样周期内的阶跃响应输出强度与作用时间对比如图3所示。

2.2 不完全微分PID与PID控制的仿真对比

在初始前放电压为±0.5 V的方波，非定常值干扰力矩的初始条件下，针对2.1节中的惯性稳定回路数学模型，分别采用PID控制和不完全微分PID控制对稳定回路进行校正，对比干扰力矩下稳定平台转动角速度输出曲线，如图4所示。

由图4可知，不完全微分PID控制相较于PID控制，其系统响应曲线超调量明显降低，响应速度也得到提高。微分环节有助于加快系统的响应速度，减小超调量，但同时会使得系统抑制干扰的能力减弱[19]。经典PID数字控制的微分环节只在第1个采样周期内起作用，不能按照系统偏差信号的变化趋势在整个调节过程中起作用，且微分在第1个采样周期内作用很强，易引入高频干扰量降低系统抗干扰能力或是产生溢出现象。

图4 不完全微分PID与PID控制下系统输出对比

不完全微分PID数字控制很大程度地削弱了微分项在第1个采样周期内的输出强度并拉长了微分的作用时间，使得数字控制器输出的微分作用能在各个采样周期按照偏差信号的变化趋势均匀地输出，从而提高系统响应速度，减小超调量并一定程度地提高了系统地抗高频干扰的能力，改善系统的性能，但对于低频干扰力矩的抑制效果并不明显。

3 扰动观测器/不完全微分PID复合控制器设计

3.1 扰动观测器基本原理

通过2.2节仿真实验可知，不完全PID控制虽然提高系统响应速度，改善动态性能，但对于低频干扰力矩的抑制效果并不明显。为更好的抑制低频扰动对控制系统带来的影响，拟在不完全微分PID控制的基础上设计扰动观测器，即实现复合控制。其中扰动观测器的主要思想是通过测量实际系统输出并和标称模型输出进行对比，估计可能存在的外部干扰和因系统模型建立不准确而带来的误差总和，并将此估计值反馈补偿给控制系统，达到消除干扰的目的。其原理如图5所示。

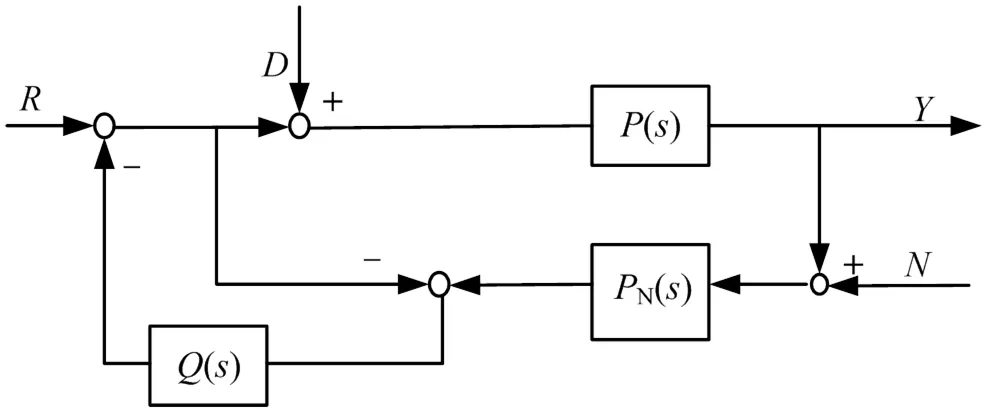
图5 扰动观测器的原理框图

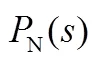
3.2 基于扰动观测器的复合控制器设计

结合平台稳定回路结构、工作原理以及扰动观测器的设计思想，本文设计了一种扰动观测器以补偿外界干扰对稳定回路造成的影响，并与不完全微分PID控制相互配合，进一步提高平台系统的鲁棒性。其原理如图6所示。

图6 稳定回路复合控制原理框图

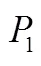
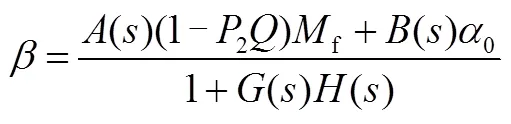
式中

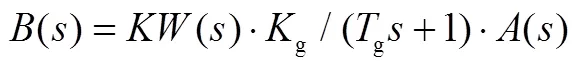
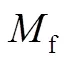
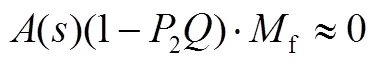
4 实验验证

为验证加入扰动观测器的复合控制方法对平台转动时低频干扰的抑制效果，在相同非常值干扰力矩影响下，分别对不完全微分PID的经典控制稳定回路和基于观测器的复合控制稳定回路进行仿真对比，分析框架轴转动角速度输出曲线。

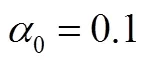
在相同初始条件下，对不完全微分PID控制及复合控制方法分别进行仿真试验，对比两种控制方法对平台框架轴抗干扰能力的影响。

图7 平台框架轴角速度在两种控制方法下的输出对比

图8 系统跟踪误差在两种控制方法下的对比

由图8可知，加入扰动观测器的复合控制可以在不影响系统动态特性的同时，显著提升稳态特性。其中框架轴最大摇摆幅度由0.2 rad/s降至0.03 rad/s，系统跟踪误差最大摇摆力矩幅度由0.015 N降至4×10-4N。

同时可以看出，由于高阶系统与扰动观测器的滤波作用，高斯白噪声对系统跟踪误差的影响很小，而对于框架角速度输出，虽然也存在一定的滤波作用，高斯白噪声的加入依然会使平台框架轴在稳定位置发生一定程度的摇摆和抖动。因此，基于观测器的复合控制可以在不影响不完全微分PID的控制品质的同时，显著提升系统稳定状态时抑制低频干扰的能力，改善系统的稳态特性，但对于功率谱密度在整个频域内均匀分布的白噪声而言，其抑制效果有待提高。

为进一步确定扰动观测器合适的低通滤波器时间常数，这里选取不同取值的时间常数进行过仿真试验，得到框架轴稳定时的角速度变化情况如图9所示。

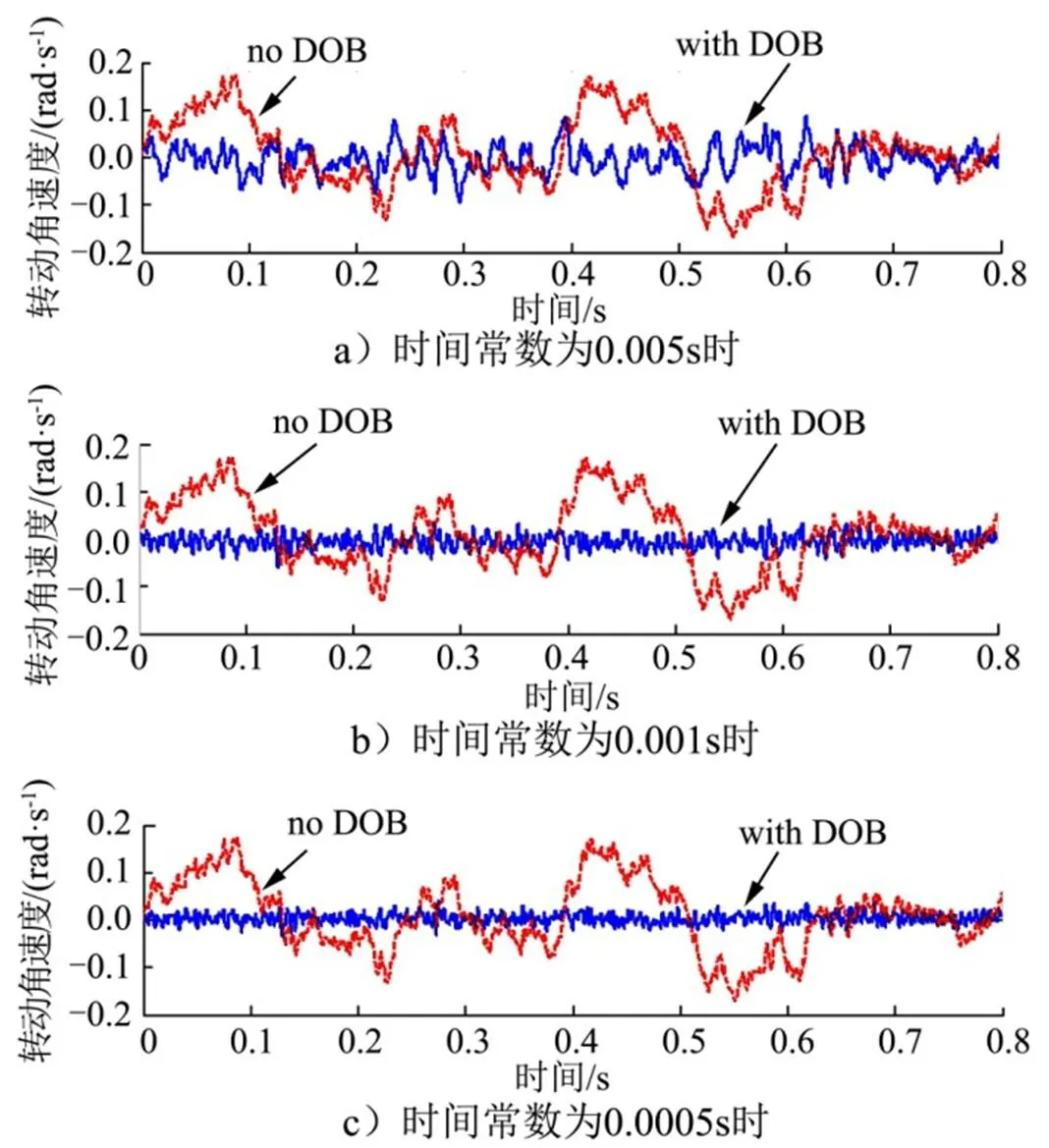
图9 平台框架轴在两种控制方法下的稳态输出对比

由图9可知，当调整扰动观测器的低通滤波器时间常数可以一定程度地改变系统抗干扰能力，当时间常数减小，滤波带宽提高时，系统的干扰抑制能力更强。但并不能说明滤波器的时间常数越小越好，时间常数过小不仅不易工程实现，还可能会降低扰动观测器的稳定性，使系统发生谐振。因此，滤波器时间常数的选取要在系统扰动抑制效果与稳定性之间权衡。应根据实际系统合理选择。

对比于其他控制方法，自抗扰控制及自适应控制方法由于需要大量参数的试凑及高阶权值矩阵的迭代，较为适用于双自由度陀螺稳定平台为代表的二阶系统，而以单自由度陀螺仪组成的高阶系统为被控对象，基于观测器的复合控制方法可以很大程度上减小计算量。此外，不同于∞鲁棒控制、变结构控制等纯鲁棒控制，复合控制将观测器与不完全微分PID相结合，在保证系统的低超调，快响应速度的同时，可以将平台框架轴在低频干扰力矩下的摇摆幅度降低一个量级，很大程度地改善系统的稳态特性，提高系统的鲁棒性。

5 结 论

本文以单自由度积分陀螺仪构成的平台稳定回路为研究对象，对系统的校正网络展开了研究。首先采用不完全微分PID控制可以对经典PID控制中的微分环节进行改进，以削弱微分环节在第1个采样周期内的输出强度，拉长微分作用时间，使系统响应输出的动态品质得到提高。针对经典控制理论的系统鲁棒性不好的问题，本文提出了扰动观测器与不完全微分PID相结合的方法对稳定回路进行校正，并对这一复合控制稳定回路的抑制干扰能力进行实验仿真。仿真结果表明，对比于常规PID控制方法，扰动观测器/不完全微分PID复合控制可以在提高稳定回路响应速度、减小超调量的同时，大幅提高系统抑制低频干扰的能力，改善稳态性能。

[1] 徐景硕, 周胜明, 蒋华君. 惯性导航系统的发展及其关键技术综述[J]. 科技信息, 2009, 35(2): 865-866.

Xu Jingshuo, Zhou Shengming, Jiang Huajun. Overview of the development and key technologies of inertial navigation system[J]. Science and Technology Information, 2009, 35(2): 865-866.

[2] 周徐昌, 沈建森. 惯性导航技术的发展及其应用[J]. 兵工自动化, 2006, 25(9): 5-56.

Zhou Xuchang, Shen Jiansen. Development and application of inertial navigation technology[J]. Ordance Industry Automation, 2006, 25(9): 55-56.

[3] 祝彬, 郑娟. 美国惯性导航与制导技术的新发展[J]. 中国航天, 2008, 1(1): 43-45.

Zhu Bin, Zheng Juan. New development of inertial navigation and guidance technology in the United States[J]. CASC, 2008, 1(1): 43-45.

[4] 吴俊伟. 惯性导航基础[M]. 哈尔滨: 哈尔滨工程大学出版社, 2001.

Wu Junwei. Inertial navigation foundation[M]. Harbin: Harbin Engineering University Press, 1990.

[5] 付常亮, 王玮. 三轴旋转式惯导平台框架控制耦合问题研究[J]. 微型机与应用, 2015, 34(4): 79-82.

Fu Changliang, Wang Wei. Research on control coupling of three axisrotary inertial navigation platform frame[J]. Microcomuter and Its Application, 2015, 34(4): 79-82.

[6] 杨阳. 数字式双轴陀螺稳瞄控制系统设计[D]. 南京: 南京理工大学, 2013.

Yang Yang. Design of digital biaxial gyro stabilized sight control system[D]. Nanjing: Nanjin Uniersity of Science and Technology, 2013.

[7] 贾福利. 平台稳定回路数字控制器的研究[D]. 哈尔滨: 哈尔滨工业大学, 2006.

Jia Fuli. Research on digital controller of platform stabilization loop[D]. Harbin: Harbin Institute of Technology, 2006.

[8] Ang K H, Chong G. PID control system analysis design and technology[J]. IEEE Trans. Syst. Tech, 2005, 13(4): 559-576.

[9] 贡志波, 朱天辉, 彭鹏, 等. 平台式惯导系统伺服回路故障分析与改进措施[J]. 西安航空学院学报, 2017, 35(3): 12-15.

Gong Zhibo, Zhu Tianhui, Peng Peng, et al. Fault analysis and improvement measures of servo loop for platform inertial navigation system[J]. Journal of Xi'an Institute of Aeronautics, 2017, 35(3): 12-15.

[10] 宋金来，甘作新，韩京清. 自抗扰控制技术滤波特性的研究[J]. 控制与决策, 2003, 18(1): 110-119.

Song Jinlai, Gan Zuoxin, Han Jingqing. Study on the filtering characteristics of auto disturbance rejection control[J]. Control and Decision, 2003, 18(1): 110-119.

[11] 魏宗康. 动调陀螺四轴平台系统建模及其智能控制设计[D]. 北京: 中国运载火箭技术研究院, 2001.

Wei Zongkang. Modeling and intelligent control design of dynamically tuned gyroscope four axis platform system[D]. Beijing: China Launch Vehicle Technology Research Institute, 2001.

[12] 王合龙, 朱培申, 姜世发. 陀螺稳定平台框架伺服系统变结构控制器的设计和仿真[J]. 电光与控制, 1998, (2): 24-29.

Wang Helong, Zhu Peishen, Jiang Shifa. Design and simulation of variable structure controller for gyro stabilized platform frame servo system[J]. Electronics Optics & Control, 1998, (2): 24-29.

[13] 朱明超, 刘慧, 张鑫, 贾宏光. 惯性稳定平台自适应前馈控制[J]. 光学精密工程, 2015, 23(1): 141-148.

Zhu Mingchao, Liu Hui, Zhang Xin, Jia Hongguang. Adaptive feedforward control for inertial stabilized platform[J]. Optical Precision Engineering, 2015, 23(1): 141-148.

[14] 杨曌. 基于现代控制理论的电机应用实例[J]. 2013, 43(2): 33-35.

Yang Zhao. An example of motor application based on modern control theory[J]. 2013, 43(2): 33-35.

[15] 舒骏逸. 两轴四框架跟踪平台伺服控制系统的设计与实现[D]. 北京: 北京理工大学, 2016.

Shu Junyi. Design and implementation of servo control system for two axis and four frame tracking platform[D]. Beijing: Beijing Institute of Technology, 2016.

[16] 刘胜. 自动控制原理[M]. 北京: 国防工业出版社, 2012.

Liu Sheng. Principle of automatic control[M]. Beijing: National Defense Industry Press, 2012.

[17] 徐江华. 自整定PID控制的理论、软件及应用研究[D]. 上海: 上海交通大学, 2004.

Xu Jianghua. Research on theory, software and application of self tuning PID control[D]. Shanghai: Shanghai Jiao Tong University, 2004.

[18] Shinskey F G. Process control systems[M]. New York: McCraw-Hill, 1979.

[19] Abdo M M, et al. Stabilization loop of a two axes gimbal system using self-tuning PID type fuzzy controller[J]. ISA Trans., 2014, 53(2): 591-602.

[20] Hirata K, et al. Stability analysis of disturbance observer based controllers for two-wheel wheelchair systems[J]. Adv Robot., 2014, 28(7): 67-77.

Disturbance Observer/Incomplete Differential PID Compound Control for Inertial Stabilized Platform

Zhong Jing-jia, Yang Gong-liu, Wang Ting, Yu Pei

(School of Instrumentation Science and Opto-electronics Engineering, Beihang University, Beijing, 100191）

In order to improve the steady-state performance of inertial stabilized control loop, a compound control algorithm combining disturbance observer (DOB) with incomplete differential PID is proposed. The DOB is used to observe the external disturbances in the control loop and compensate it to the original system. It improves the stability of the system while enhancing the disturbance rejection and robustness. The simulation results show that the disturbance observer / incomplete differential PID compound control algorithm can significantly improve the steady-state performance of the inertial stabilized platform. Compared to the conventional PID control, the compound control method not only improves the response speed of the system, but also improves the disturbance rejection capability of the system and the stability accuracy.

inertial stabilized platform; disturbance observer; incomplete differential PID; disturbance rejection

V448

A

1004-7182(2020)02-0072-06

10.7654/j.issn.1004-7182.20200214

钟婧佳（1994-），女，助理工程师，主要从事导航、制导与控制的研究。

杨功流（1968-），男，研究员，博导，主要从事导航与控制方向的研究。

王 汀（1972-），男，研究员，博导，主要从事导航、制导与控制的研究。

于 沛（1989-），女，博士研究生，主要从事导航、制导与控制的研究。

2019-06-01；

2019-09-19