基于遗传算法的高过载永磁伺服电机设计与优化
2020-04-20秦璧勋赵世伟招家鑫杨向宇
秦璧勋,赵世伟,招家鑫,杨向宇
(华南理工大学 电力学院,广州510640)
0 引 言
在工业伺服领域,电机经常运行在负载间歇突变的工况。而在系统对动态响应能力要求较高的应用场景中,要求电机负载出现急剧变化时,电机的输出转矩要能跟随负载的变化,转速也要保持恒定值不能下降。因此,研究高过载能力的电机,在指定尺寸之内使得电机尽可能输出高的功率,这种提升极限输出转矩能力的电机具有普遍的应用意义。
电机在其转矩超过额定转矩时,输出转矩不会随着输入电流呈线性增长,而是出现饱和现象。在过载状态下,电机出现定子铁心饱和、电枢反应过强、直轴去磁作用过大、电机温升过高和电机可靠性下降等现象[1]。
针对上述限制因素,文献[2]采用增加永磁体厚度和加大气隙长度来增强电机短时过载能力。在电机过载时,为防止磁钢出现不可逆退磁现象,分析了不同厚度的最大去磁工作点;并确定永磁体厚度从性能上使电动机的直轴电抗合理以及反电动势合理。分析了气隙长度与短时过载能力的计算曲线,得出在一定区间内随着气隙长度的增加,电抗参数减少,电机的短时过载能力增加的结论。在转子结构上,文献[3]提出因内置式永磁电机电枢反应电抗高于表贴式电机,而使得在相同大小的电流激励下,内置式电机的反电动势增长更快而超过控制器输出电压的结论,因此在相同控制器电压情况下,表贴式电机过载能力更强。存在的问题是两者对比时,没有控制其余影响电机电枢反应电抗的参数相同,例如定子裂比,定子槽尺寸以及导体数、绕组形式等。内置式永磁同步电机可以通过改善其转子结构和绕组形式来减小交直轴电抗,并且由于交直轴磁路存在差异会产生磁阻转矩;而凸极率高的结构产生的磁阻转矩最高比例可占总电磁转矩40%[4],因此可利用磁阻转矩显著提升电机的过载能力,并扩展电机恒功率运行的范围。
遗传算法(GA)最早于1975年由密歇根大学的 Jonh Holland 在解释自然界中的生物适应性过程中模仿物种进化的原理所构造的人工系统的模型,它以自然选择和演变过程为基础并且不需要求导,模拟生物进化过程中类似于遗传、变异的过程,是一种以“优胜劣汰,适者生存”规则来求取最优解的全局收敛算法[5]。本文以极限转矩、转矩波动和波形畸变率为优化目标,构造多目标函数,根据场路结合法计算并结合样机制造的工业标准微调后的模型参数作为初始种群,采用遗传算法对电机参数进行优化,进一步提升了电机性能。
1 PMSM输出转矩分析
分析PMSM常用的方法是用dq轴数学模型。取转子永磁体基波磁场轴线为d轴,q轴逆时针超前d轴90°,建立永磁同步电机dq轴数学模型。
电压方程:
(1)
(2)
磁链方程:
ψd=Ldid+Lmdif
(3)
ψq=Lqiq
(4)
电磁转矩方程:
Tem=p(ψdiq-ψqid)
(5)
式中,u为电压,i电流,ψ为磁链,下标d、q分别表示各物理量在d轴、q轴的分量;R1为电枢绕组电阻,ω为电机角速度,Ld、Lq为dq轴等效电枢电感,Lmd为定转子间dq轴互感,if为永磁体等效励磁电流,Tem为电机电磁转矩,p为极对数。
图1为PMSM的空间矢量图,其中β为定子磁链和永磁体产生的磁链的空间电角度,θ为转子位置角。
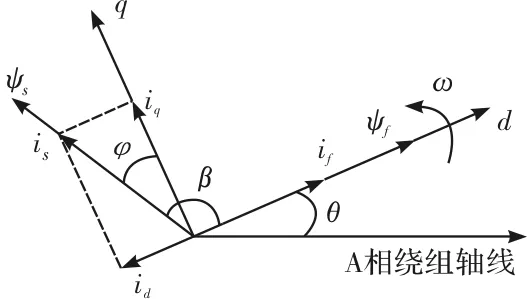
图1 PMSM空间矢量图
将式(3)、式(4)代入式(5),并根据图1中定子电流空间矢量关系,将电磁转矩进一步表示为空间矢量形式:
Tem=p[Lmdifissinβ+(Ld-Lq)idiq]=
p[ψffiq+(Ld-Lq)idiq]
(6)
上式表明,永磁同步电机的力矩包含两个部分:一部分是pψfiq,为永磁电机的永磁转矩Tm;另一部分p(Ld-Lq)idiq,是由于转子不对称,即由于磁路上磁阻不均匀产生的磁阻转矩。此次设计内置式永磁电机属于凸极电机,为提高磁阻转矩,从电机磁路结构方面考虑,可以加大磁路的不对称性,即在磁路设计上,可以提高凸极率作为目标。
(7)
将式(7)代入式(6),输出转矩为
(8)
式中,ψf为永磁体磁链,ψf=E0/ω,E0为空载反电动势;i1定子相电流有效值;φ为i1和E0夹角,也称内功率因数角;ΔL为Ld-Lq。
式(8)对φ求导,得到:
(9)
令式(9)为零,得:
(10)
对式(8)二次求导,得:
(11)
依据d2Tem/dφ2≤0时,Tem取得极大值,因此当转矩取极大值时对应的φ值为
(12)
为方便计算,取K=(Ld-Lq)|i1|/ψf,进一步得到转矩最大值为
(13)
由上式可以看出,影响永磁同步电机的峰值转矩的主要因素为极对数p、空载反电动势E0、电枢电流I1、交轴电感Lq、直轴电感Ld等参数。
其中,空载反电动势E0主要和主磁通大小φ有关,而永磁电机运行过程中磁通和磁动势由永磁体提供,因此可以改变永磁体尺寸或性能来合理设计E0,进而提升峰值转矩。
另一方面,由于内置式永磁同步电机的交、直轴磁路都经由定、转子齿部,气隙和定子轭部闭合,因此交、直轴电抗和定子齿部宽度,定子槽宽度、高度以及气隙长度等参数有关,考虑到样机加工的工艺限制,气隙长度不宜取得太小,选取的范围有限,因此不予考虑其影响。
综上所述,本次研究的重点是分析出定子齿部宽度,定子槽高度和永磁体尺寸等参数对电机过载能力的影响规律。
2 IPMSM过载能力研究
2.1 设计方案
参照安川伺服电机SGM7A-20A,设计一台额定功率为2 kW( 8极、24槽) 的永磁同步电动机,并进行有限元仿真验证设计的理论,初步电机设计方案的要求和对照电机的参数如表所示。
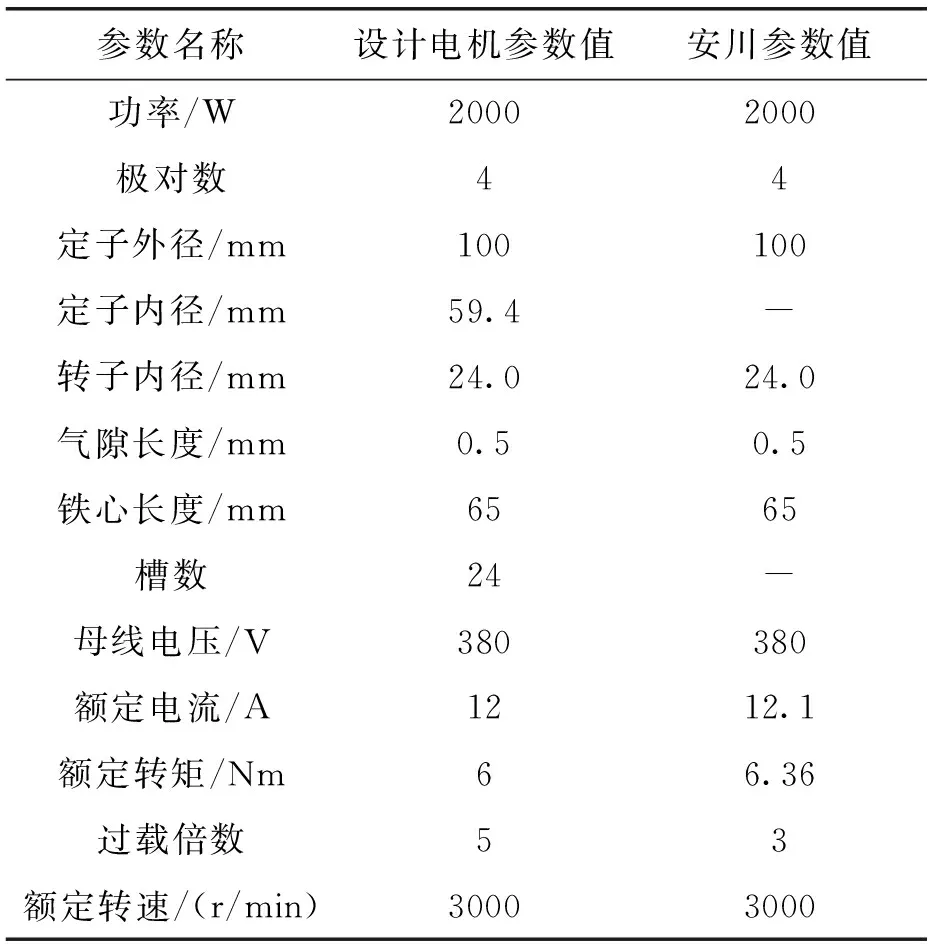
表1 电机设计主要参数
图2 初选电机模型图
2.2 齿部宽度和槽高度对过载能力的影响
高过载电机运行中需要数倍级的额定电枢电流,需要更多的电负荷,则需要更大的槽面积容纳导线,减少电机的铜耗,最终提高输出转矩。但是齿槽宽度比过小,较小的齿面积会则会让电机更早出现磁饱和现象,铁耗则会增加,电机效率降低,输出能力降低,铁心发热电机温升增高等不利影响。考虑到在过载时铜耗是电机损耗的主要因素,铁耗可以忽略,因此,本次设计中电机的磁负荷研究主要集中在如何提高峰值转矩。
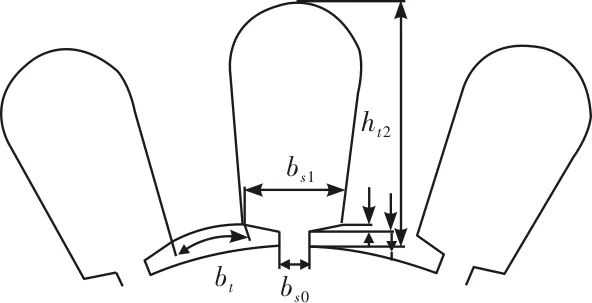
图3 定子冲片图
表1着重分析了在7倍额定电流情况下,不同齿部宽度bt对电机进入饱和运行区的分析,仅改变了齿部宽度bt和并同时调整导体数和导体截面积来控制槽满率接近75%,其他尺寸参数保持不变。
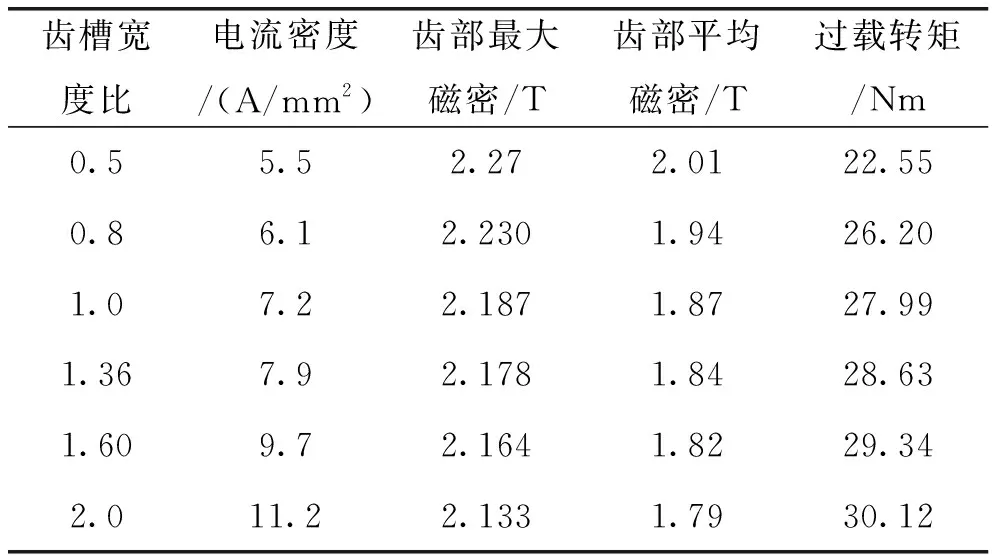
表2 齿部宽度对电机参数影响
(其中,电流密度为额定电流所对应的电流密度,齿部最大、平均磁密为7倍额定电流时对应的值。)
上表结果表明:齿槽宽比越小时,齿部磁密越饱和,过载转矩越低;齿槽宽比越大时,齿部磁密更低,有利于实现高的过载转矩。
但矛盾之处在于齿槽宽比越大时,槽面积越少,电流密度会增加,热负荷上升显著。考虑到热负荷的限制,根据经验,永磁电机电流密度一般选择在8A/mm2以下,因此齿槽宽度比在1.36附近最为合适,满足散热要求的同时较其他比例更不容易进入饱和区间,有利于实现转矩更高过载。
图4 齿部磁密测量位置
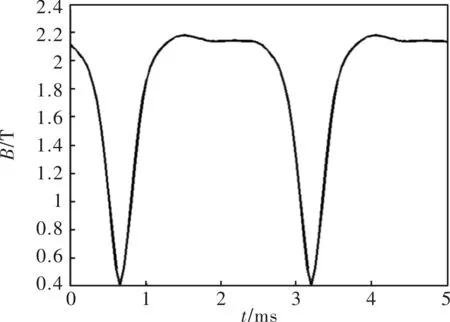
图5 过载运行时齿部磁密图(齿槽宽比1.36)
槽高度ht2的变化对输出转矩造成影响在两方面:从上表可分析出,在一定范围内,电机过载输出转矩随着槽高度降低而增大,另一方面转矩脉动呈现上升的状态。槽高度的减小可以拓展轭部高度,降低轭部饱和程度,但考虑到槽高过小时,转矩脉动较大的问题以及电枢绕组空间过小的问题,因此轭高应该给予一定裕量,故控制槽高ht2为9 mm。
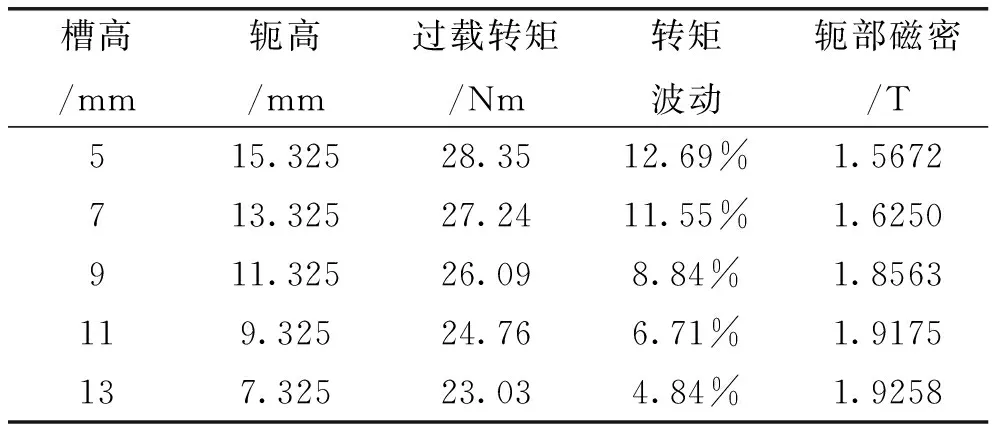
表3 槽高对电机参数影响
2.3 永磁体厚度对过载能力的影响
永磁体在运行中,作为磁源向外磁路提供磁动势。增加永磁体厚度,能提高每对极磁动势幅值,这样可以增加磁负荷提高最大输出转矩。
表4详细分析了在5倍过载电流情况下,随着永磁体厚度增加时,感应电动势以及过载比和定子齿轭部磁密变化情况。
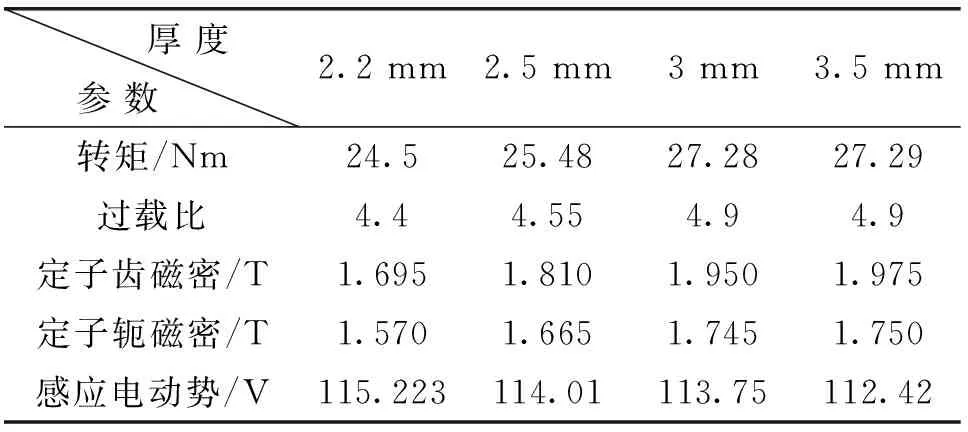
表4 永磁体厚度对电机参数影响
结果表明,随着永磁体的厚度增加,输出转矩有所提高,过载比在一段区间内显著上升,并且定子磁饱和情况也会更饱和;另一个变化情况是随着厚度增加,感应电动势有所下降,原因是在磁动势回路中,磁钢本身也是磁阻,并且磁导率和空气相当,因此在厚度增加时,磁阻越大,绕组的电感越小,减弱了电枢反应的影响。
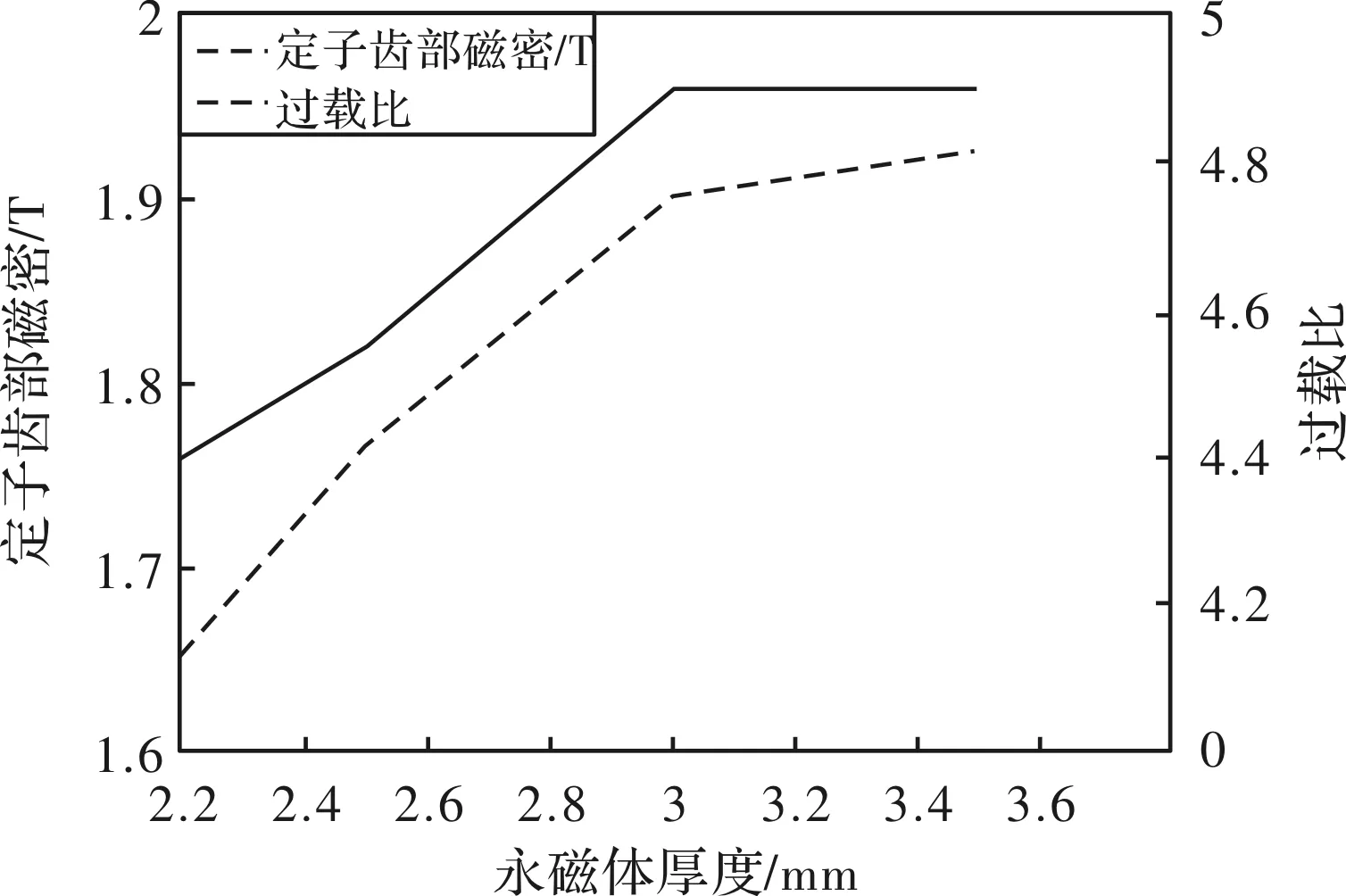
图6 永磁体厚度对过载比和磁饱和的影响
图(3)从表(3)中单独分离出永磁体厚度对过载比和定子铁心磁饱和度影响的情况。
从图中可以看出永磁体厚度越厚时,过载比和输出能力能进一步提高,但是一方面从磁饱和度限制的情况来看,定子齿部磁密一般不超过1.85T,厚度超过3 mm继续增加时,定子齿部磁密越容易进入饱和非线性区间;另一方面,从节约成本的角度看,厚度3 mm已经可以接近5倍过载的需要,进一步增加厚度所提升的空间有限。因此从两个角度分析后,设定永磁体的厚度为3 mm。
2.4 过载能力的评定
为了检验设计的电机转矩输出性能,进行了有限元仿真分析,通过改变输入电流,分别输入1倍到8倍(间隔0.5倍)的额定电流观察输出转矩。各倍数额定电流激励下的输出转矩情况如图4所示。
由上图分析可知,当输入电流达到84 A,即额定电流的7倍时,转矩增长见缓,并且继续增加电流时,转矩增长趋于饱和;且输入电流达到84 A时,感应电动势有效值为145.56 V,其对应的线电压幅值为356.54 V,尚在母线电压的380 V限制范围内。
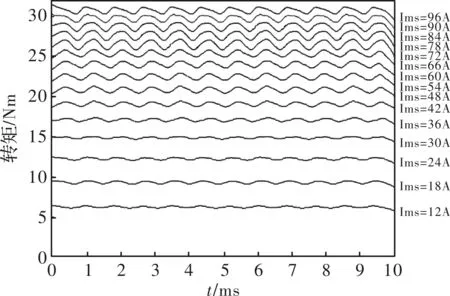
图7 不同电流激励下的输出转矩
由于控制器容量限制,所以在电机最高输入电流限制下,选定额定电流7倍的值作为最高电流,此时电机输出转矩接近30 Nm,过载倍数接近5倍。
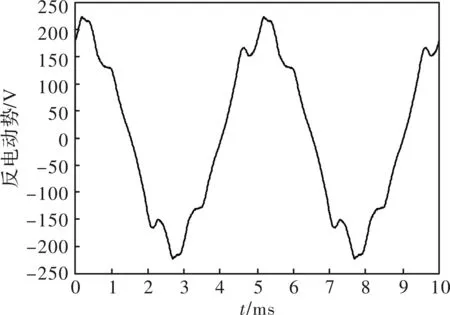
图8 7倍额定电流一相感应电动势波形
3 遗传算法优化
3.1 遗传算法基本原理
遗传算法(GA)的求解过程可分为以下步骤:
1)编码
对优化问题中每个自变量用设定的编码方案编码成有限长度的字符串,由n个自变量字符串组成的1条染色体,对应于1组电机结构参数。
2)确定种群大小
种群大小即为染色体的数目,它是由所有可能的解组成的解集。
3)评估适应度
遗传算法按照个体适应度来评估其遗传至下一代的概率。通常要先算出每个个体目标函数大小,按照一定转化规律转化为适应度。
4)选择
选取优良的个体进行繁殖,来构成下一代群体。
5)交叉
对于上一步已选中的个体,随机选中染色体的某位置,将双亲的该位置遗传信息予以互换,其余位置的基因不变,以此产生两个后代。
6)变异
变异是随机选中个体对其随机进行某一位置的基因信息进行反转,变异以一定概率进行并且和交叉配合有效增加种群多样性,克服早熟等缺点。
本次优化的基本遗传算法流程图如图9所示。
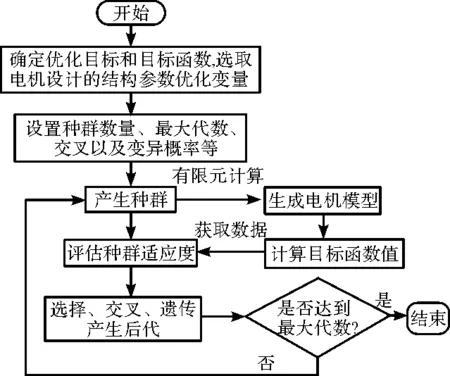
图9 IPMSM基本遗传算法流程图
3.2 优化设计的数学模型建立
1)优化变量的选取
理论上讲,电机所有结构参数均可作为优化设计变量,实际上,一般选取对电机优化目标影响较大的参数即可。考虑气隙磁场对转矩影响较大,经过理论分析及大量仿真发现下列尺寸对电机的转矩具有较大影响:永磁体磁化方向长度HM、永磁体底部到转子内径距离O2、相邻两极间距离RIB、转子外径DO2、铁心轴向长度LEF等5个变量,因此上述变量可作为优化设计变量,在保证定子外径以及气隙长度不变前提下,这些相关参数是综合考虑了电机性能和实际加工制作后所选取的。记设计变量为
x=[x1,x2,x3,x4,x5]T=
[HM,O2,RIB,DO2,LEF]T
(14)
相关优化参数变化范围以及模型图如图10所示。
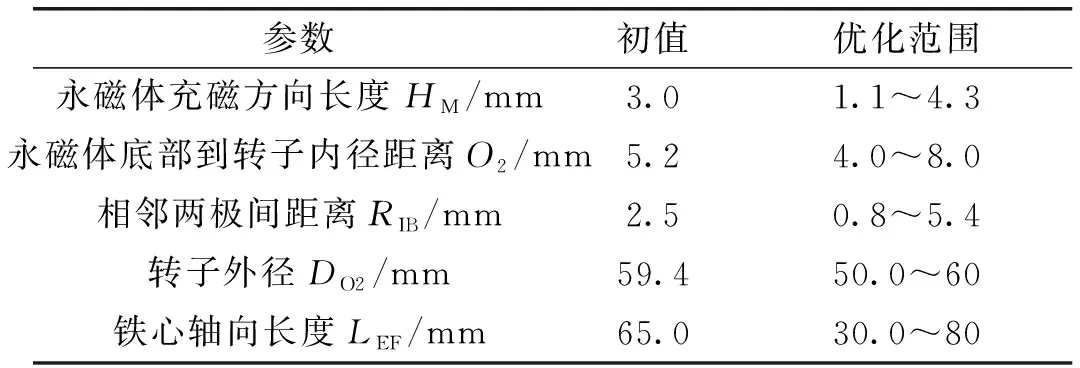
表5 主要优化参数的初值和变化范围
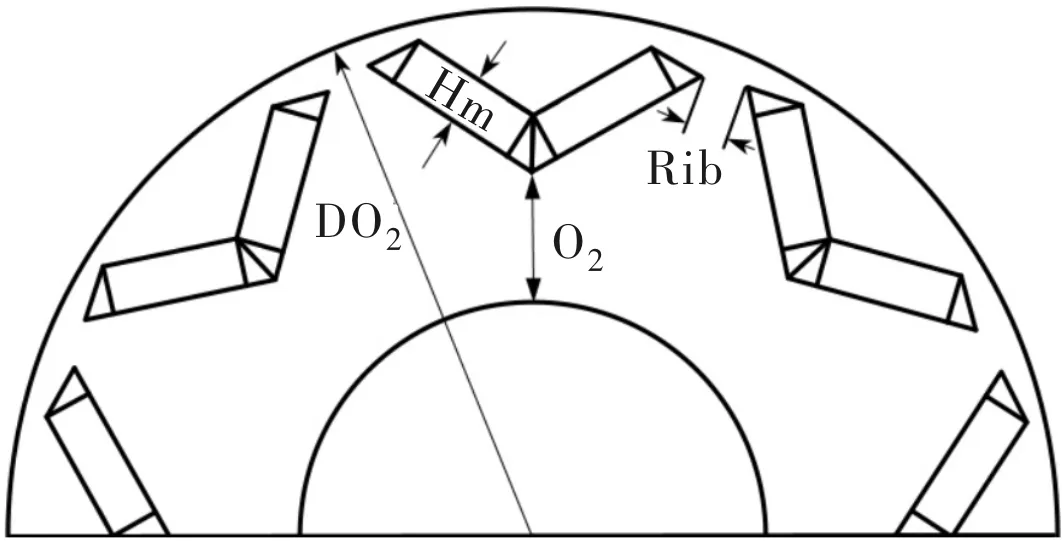
图10 IPMSM优化参数模型图
2)目标函数的确定
在本次电机优化设计过程中,过载能力作为设计的重要目标要优先考虑,其次考虑到电机运行性能,因此结合波形畸变率作为设计目标,建立的目标函数如下:
minf(X)=-ω1×T/T0+ω2×THD/THD0+1
(15)
式中,ω1和ω2为权重系数,满足ω1+ω2=1,此次优化取ω1=0.6,ω2=0.4,主要优化提升转矩的同时兼顾降低转矩脉动以及波形畸变率;T是转矩,负号目的是为了最大值;THD是空载气隙磁密波形畸变率,期望是最小;T0和THD0是为了消除两个目标的数量级差异而设置的基准值。
3)约束条件的设置
电机优化设计中需要设置约束条件以满足实际要求和工艺限制,同时是为了引导优化过程的向包含目标最优解的可行域进行搜索。
本文除对数学模型的优化变量上有限制外,还考虑到在高过载情况下,定子齿、轭部磁密可能会过高的现象,因此重点对饱和现象加以约束,即选取过载情况下的定子齿部磁密Bt、轭部磁密Bj进行限制,另外还选取其余性能约束,包括气隙磁密Bδ、效率η、过载转矩T以及槽满率Sf加以约束。根据综合设计经验数据以及数学模型的边界范围, 选择变量约束和函数约束如下:
(16)
永磁同步电机优化属于有约束、非线性的多目标优化问题,但GA属于一种无约束优化方法,并且不能单独处理约束条件,因此引入罚函数,让目标函数与其一起构成无约束的增广目标函数,当适应度函数中出现违反约束的个体时,罚函数予以惩罚,因此可以转化为无约束优化问题。罚函数构建如下:
(17)
其中,H(y)为阶跃函数:
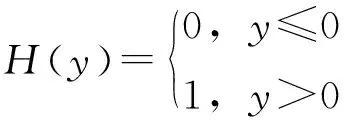
(18)
因此,增广目标函数为
F(x)=f(x)+p(x)
(19)
3.3 优化前后结果对比

表6 主要优化参数优化前后数值对比
为验证GA优化算法的有效性,下面对比分析了优化前后IPMSM的电磁性能:
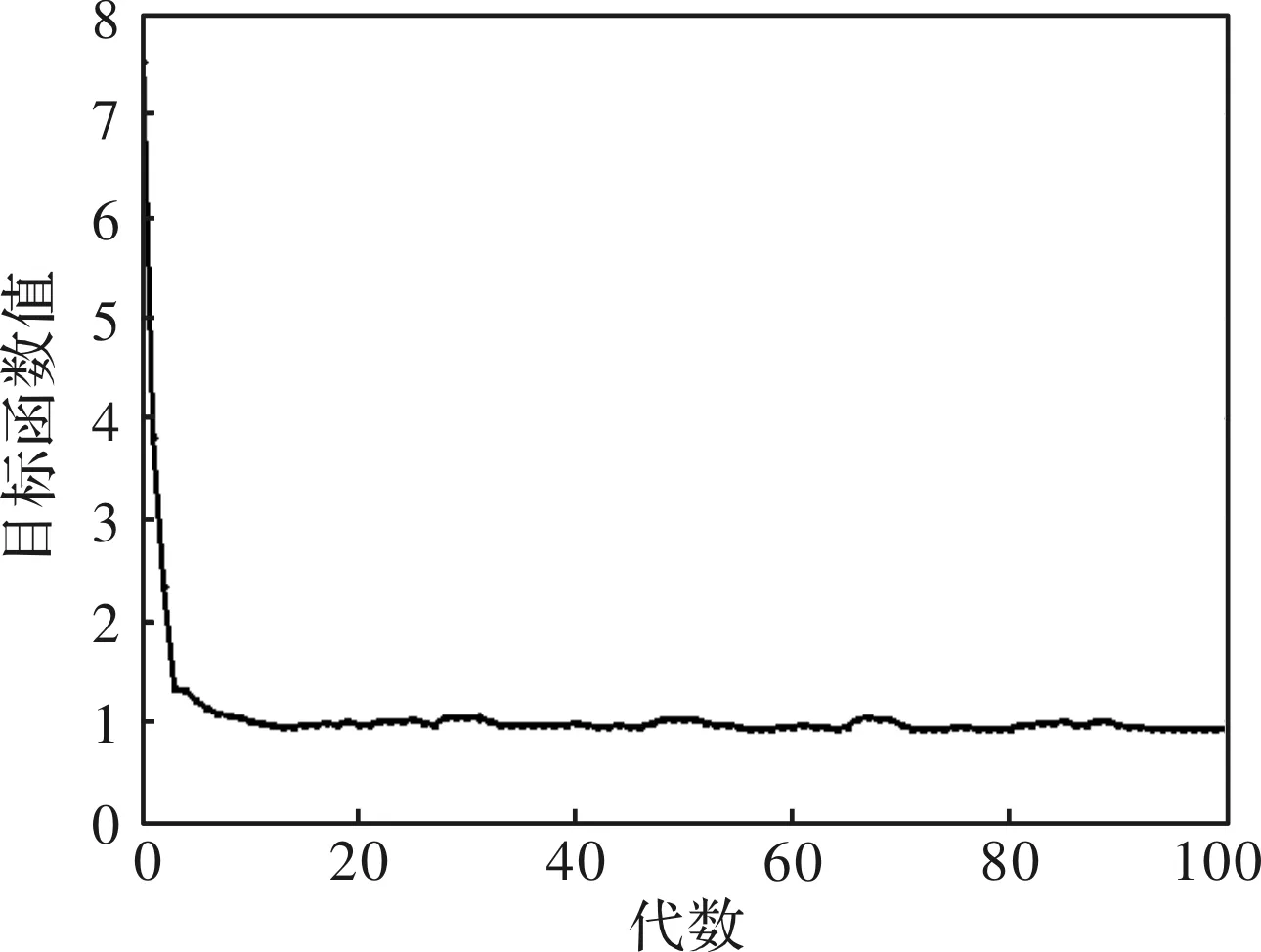
图11 遗传算法目标函数值
首先遗传算法的目标函数值经过数代优化后此后逐渐收敛到1附近,优化的主要目标是峰值转矩及波形畸变率。
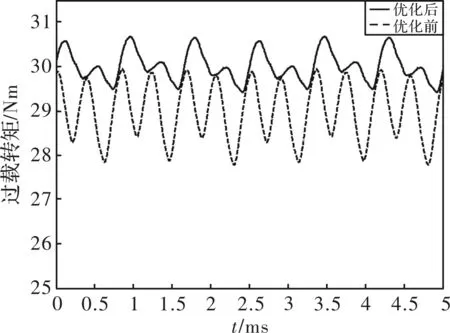
图12 优化前后峰值转矩对比图
优化之前的峰值转矩为28.49 Nm;优化后,峰值转矩达到30.20 Nm,峰值转矩提升幅度6%。
提升峰值转矩的同时对转矩脉动的抑制是很有必要的,因为转矩脉动抑制以后会对整个电机的平稳运行有很大的改善。优化后,转矩脉动从7.5%降至4.37%,提高了电机的平稳运行性。
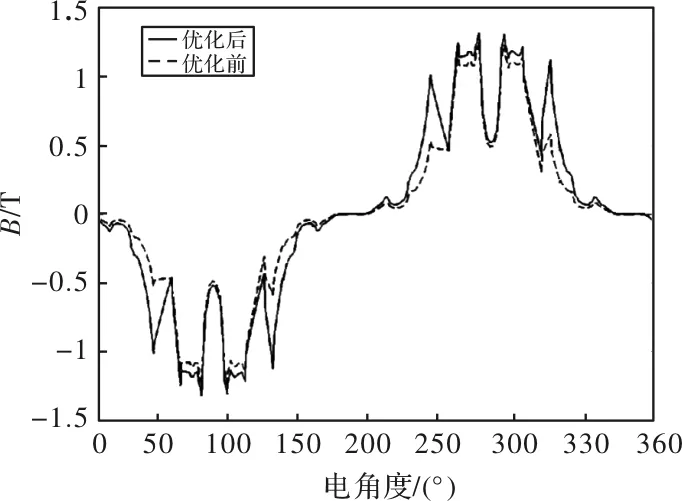
图13 气隙磁密对比图
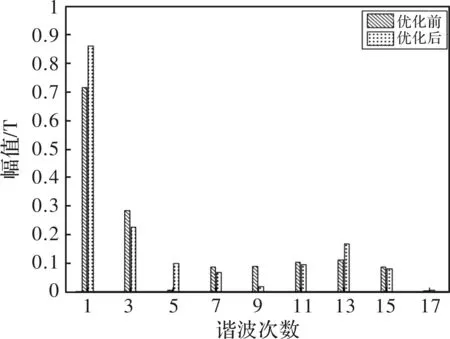
图14 气隙磁密FFT对比图
气隙磁密影响电机能输出的转矩大小,优化后的基波气隙磁密得以提高,从优化前后的波形对比上看,优化后的波形更接近正弦形状。
气隙磁密傅里叶分解图显示,优化后基波幅值上升,从0.714T提升至0.86T,除5次谐波、13次谐波外的其余高次谐波含量在优化后均得到了不同程度的抑制,表明此次优化提升了峰值转矩的同时降低了波形畸变率。
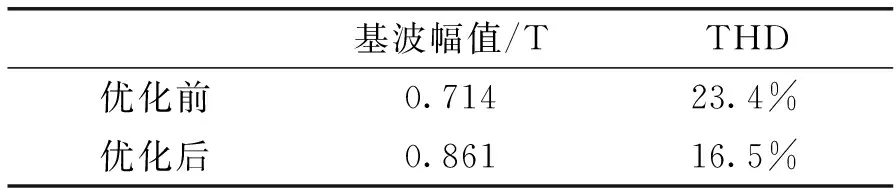
表7 优化前后性能指标对比
4 结 论
从推导永磁同步电机的极限输出转矩的公式入手,分析出一系列存在影响过载能力的因素:空载反电动势和凸极率等电磁参数,从而改变结构参数例如定子齿宽比、永磁体厚度等,在指定外径尺寸和磁饱和以及电机输入容量等边际条件内,尽可能提高电机极限输出转矩,设计出1台额定功率2 kW,并通过遗传算法优化使过载能力达到5倍的永磁同步电机。本文设计的电机过载能力和同等尺寸和同功率的常规电机相比,具有过载能力强的特点,可应用在工业伺服领域中具有极端特殊要求的场景,因此具有广阔的应用价值。
