应用新型Halbach阵列的PCB定子轴向磁通永磁电机性能分析
2020-04-20夏加宽冯小雪王晓远
夏加宽,李 响,,冯小雪,王晓远,王 达,张 晔
(1.沈阳工业大学 电气工程学院,沈阳 110870;2.国家电网沈阳供电公司,沈阳 110003;3.天津大学 电气自动化与信息工程学院,天津 300072;4.国家电网铁岭供电公司,辽宁 铁岭 112000)
0 引 言
轴向磁通永磁电机(Axial Flux Permanent Magnet, AFPM)与径向磁通永磁电机不同,气隙磁通是沿轴向的,其气隙呈平面型。由于其具有轴向尺寸短、电枢绕组电感小、无齿槽转矩、效率高等优点近年来受到越来越多的关注[1,2]。AFPM作为一种性能优异的伺服电机广泛应用于电动汽车、风力发电、航空航天等诸多领域。PCB(Printed Circuit Board)定子无铁心AFPM可以大幅度减轻电机的重量,消除了定子铁耗,无齿槽转矩,实现对线圈的准确定位,电机伺服性好,且利于批量加工生产[3,4]。但采用了PCB无铁心定子结构会使电机定子线圈交链的磁通量减少,因此在进行PCB无铁心AFPM电机设计时对气隙磁密幅值及正弦性有了更高的要求。与传统的AFPM电机不同,PCB定子电机定子绕组直接布在印制线路板上,在PCB板面积一定的条件下,定子绕组的匝数与线宽及线距呈现对立关系[5]。为了使PCB板具有一定的过流能力,同时考虑到散热问题,PCB板要具有一定的厚度,故气隙长度不可能过短。考虑到电机的重量、成本及轴向长度,PCB定子电机的转子磁钢不宜太厚。因此,优化转子磁钢磁极分布就成为了提高PCB定子电机输出性能的首选方法。
Halbach永磁体阵列在永磁电机的设计中具有广泛应用,国内外均有专家学者对Halbach永磁体阵列进行研究。文献[6]应用Halbcah永磁体阵列设计了一台盘式无铁心电机,用2D仿真结果与3D仿真结果进行了对比,并分析了90°、60°及45°Halbach永磁体阵列对气隙磁密及转矩密度的影响,但其只进行了仿真分析,没有进行实验验证。文献[7]利用矢量磁位对Halbach永磁体阵列所产生的磁场进行了解析分析,并应用到无铁心永磁同步直线电机上,结果表明高次谐波得到了明显减弱,但反电动势的幅值略有减小。文献[8]研究了以获得基波幅值极大值与正弦性畸变率极小值为多目标的混合全局优化算法。文献[9]研究了不同气隙长度及永磁体厚度对应用Halbach永磁体阵列的盘式电机的影响,但它仅改变了Halbach永磁体阵列的角度,对于Halbach永磁体阵列的形状并未进行深入的探讨。就目前来看,对于应用于AFPM电机的Halbach永磁体阵列的研究主要集中于磁钢的磁化角度,以及磁钢与背铁的厚度配比[10-14]。但对于改变Halbach永磁体阵列的磁极形状对气隙磁密及漏磁的影响,尤其是从转子的内径处及外径处分别探讨漏磁情况,一直以来鲜有研究。
本文对应用新型Halbach永磁体阵列的PCB定子无铁心轴向磁通永磁同步电机的性能参数进行了分析。该新型Halbach永磁体阵列将磁极内径处和外径处的极角参数视为相互独立的变量,由不同圆心扇形的主磁极及辅助磁极的形状,改变轴向磁化永磁体及切向磁化永磁体在内径处及外径处所占的弧长及辅助磁极使主辅磁极在磁钢上的分布更加合理。在保证永磁体用量不变即电机成本几乎不增加的前提下,使得PCB定子无铁心轴向磁通永磁同步电机的性能得到了提升。同时建立了电机的三维电磁场计算模型,利用有限元法仿真了PCB定子无铁心永磁同步盘式电机的气隙磁通密度及漏磁。针对不同形状的主磁极及辅助磁极并对气隙磁密基波幅值和正弦性畸变率并进行了对比分析。最后通过样机实验,验证了仿真结果的准确性。为PCB定子无铁心盘式电机的磁钢结构设计提供一定的参考依据和实际工程价值。
1 PCB定子AFPM性能参数分析
为了更好的分析PCB定子盘式电机的气隙磁密、漏磁情况、空载反电势等参数。本文建立了PCB定子AFPM的整机模型,如图1所示。仿真分析时,对电机模型进行了如下的假设[15]:
1)永磁体被均匀磁化,且表面光滑,拼装时两块永磁体可以实现无缝对接。
2)PCB定子线圈的磁导率近似等于空气的磁导率,故在计算空载气隙磁密时将线圈作为气隙部分处理。
3)忽略电机转动时温升对永磁体磁性及电机性能的影响。
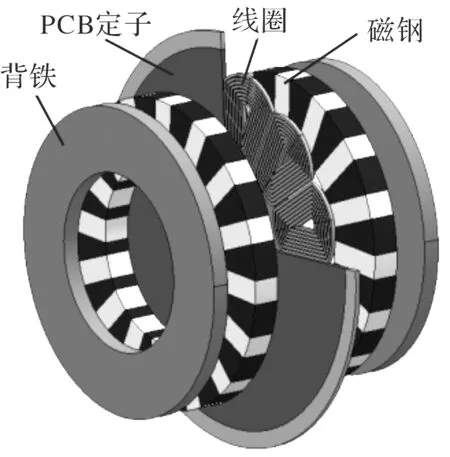
图1 PCB定子AFPM模型
电机参数见表1。
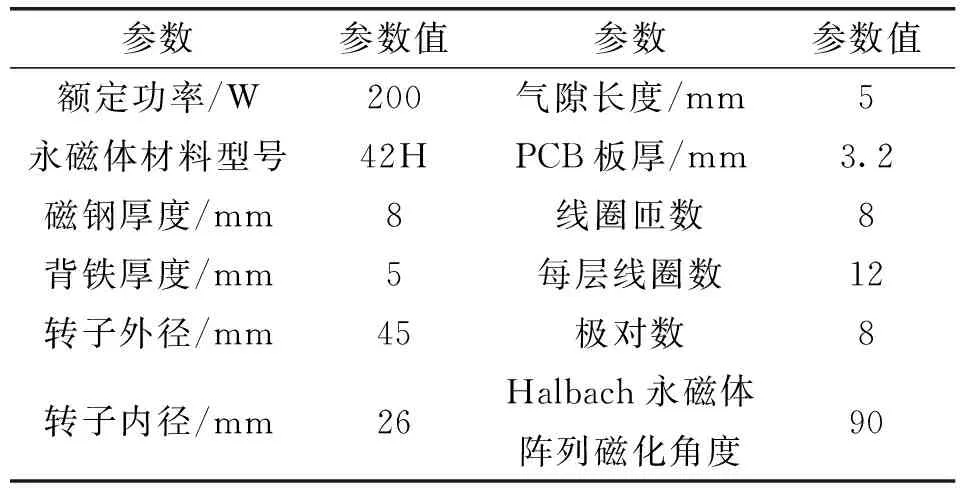
表1 电机的基本参数及设计要求
1.1 气隙磁密分析
AFPM气隙磁场为三维分布的磁场,进行三维电磁场的解析计算十分困难,故取平均半径处的磁路进行分析。
假设磁性材料为均匀磁化,则满足公式
B=μ0M+μ0H
(1)
式中,B为磁感应强度,M为磁化强度,H为磁场强度。
若将AFPM等效为2D的直线电机模型,并且假设电机沿半径方向为x轴方向,轴向方向为z方向。则Halbach型永磁体阵列的磁化强度函数可以表示为
(2)
式中,Bx与BZ分别为永磁体沿电机径向x方向和轴向z方向的磁感应强度。其表达式分别为
(3)
(4)
式中,αp为极弧系数,Br为永磁体的剩磁强度。利用麦克斯韦方程组进行电磁场计算,则AFPM气隙磁通密度的表达式为
(5)
1.2 电机输出反电势分析
本文采用的PCB定子线圈为同心式螺旋型绕组。由于PCB定子为无铁心结构,因此在这种情况下,每一匝绕组所交链的磁通量均不相同,因此需要分别对每一匝线圈分别进行分析。
对于一个单匝线圈,其产生的反电势的有效值为
Eq=4.44fΦm
(6)
其中,f为导体中感应电动势的频率,Φm为电机每极下基波磁通量。Φm可以表示为
(7)
其中,Bmax为气隙磁通的基波幅值,Si为第i匝线圈在磁极下的有效面积。
对于整个PCB定子,可以将其看成是若干匝同心线圈的组合。因此,可以分别求解每一匝线圈的绕组系数,再进行叠加。整个PCB定子的反电势有效值为
E=4.44fN∑knΦm
(8)
式中,∑kn为每匝线圈的绕组系数之和,N为PCB绕组的层数。
2 新型Halbach永磁体阵列
Halbach永磁阵列可以提高气隙磁密,并保证气隙磁密的正弦性,弥补无铁芯结构对主磁路磁通带来的负面影响,有效提高了电机的转矩密度[16]。若将90°Halbach阵列轴向磁化永磁体定义为主磁极,切向磁化永磁体定义为辅助磁极。传统AFPM轴向磁通永磁同步电机的转子多采用主辅磁极同圆心的90°Halbach永磁体阵列形式。本文新型的Halbach永磁体阵列采用主辅磁极不同圆心的结构,即是从主磁极的内径和外径与中心线的夹角处出发,研究新型Halbach永磁体阵列对电机性能的影响。转子中新型Halbach永磁体阵列磁钢参数示意图如图2所示。
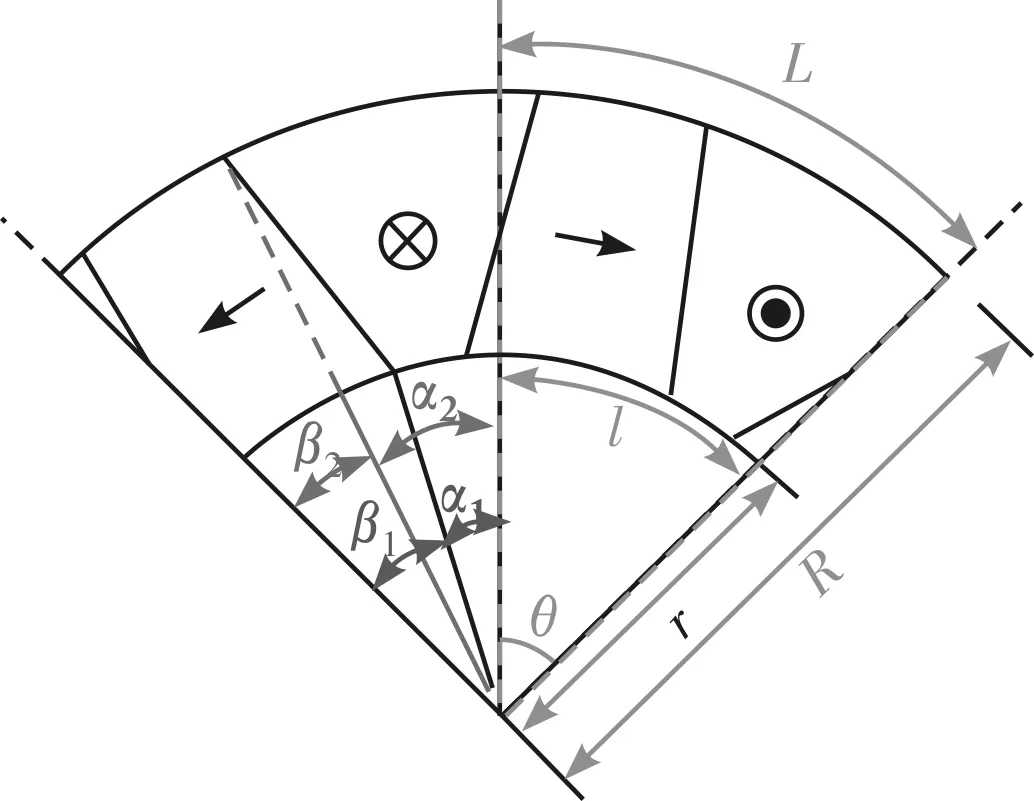
图2 新型Halbach永磁体阵列磁钢参数示意图
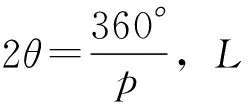
应用新型Halbach永磁阵列的PCB定子无铁心AFPM的转子模型如图3所示,其中,电机的极弧系数取1。
图3 PCB定子电机转子部分模型
3 仿真结果分析
本文采用有限元分析方法对该新型Halbach阵列轴向磁通永磁电机气隙磁通密度进行仿真分析,样机参数如表1所示。PCB定子选取8层板,12个线圈,为了方便仿真分析,认为模型中的每匝导体与自身闭合。PCB定子绕组的形状选取一种介于梯形和圆形之间的混合型绕组。这种形状混合型绕组结合了圆形绕组与梯形绕组的优势,与梯形绕组得到的电动势相差很小,且端部较短,减小了绕组电阻,在负载时减小铜耗,降低发热,使得绕组可能通过更大的电密,从而提高功率密度,增加转矩。
3.1 气隙磁通密度的评价函数
在AFPM的设计中,气隙磁通密度对电机的反电势及输出转矩有直接影响,且气隙磁通密度的正弦性也可以反映电机的漏磁。因此,本文采用一个包含气隙磁密基波幅值及各次谐波幅值的评价函数F作为评价新型Halbach永磁体阵列磁钢是否合理的主要评判参数。
(9)
式中,BZ1为气隙磁通密度沿轴向的基波幅值,BZ3、BZ5、BZ7为别为轴向磁通密度3次谐波、5次谐波、7次谐波的幅值。
3.2 气隙磁密仿真分析
本文研究了永磁体内外径极角不同时,即永磁体内外径不同圆心时,永磁体形状及分布对气隙磁密的影响。通过分别改变Halbach的永磁体在内径处及外径处与中心线的夹角即改变α1、β1及α2、β2,进而改变Halbach永磁体的形状及在磁钢上的分布。图4给出了轴向气隙磁通密度基波幅值随主磁极与内径处的夹角α1和与外径处夹角α2变化的三维散点图。为了便于观察,将该三维散点图分别以x轴和y轴为轴心,对x;z平面和y;z平面进行投影,结果如图4(a)和图4(b)所示。
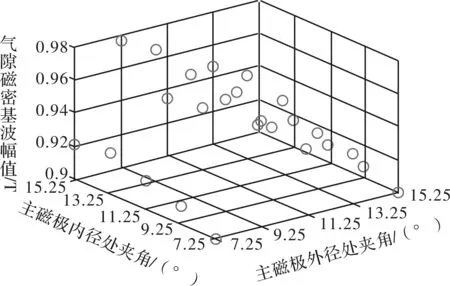
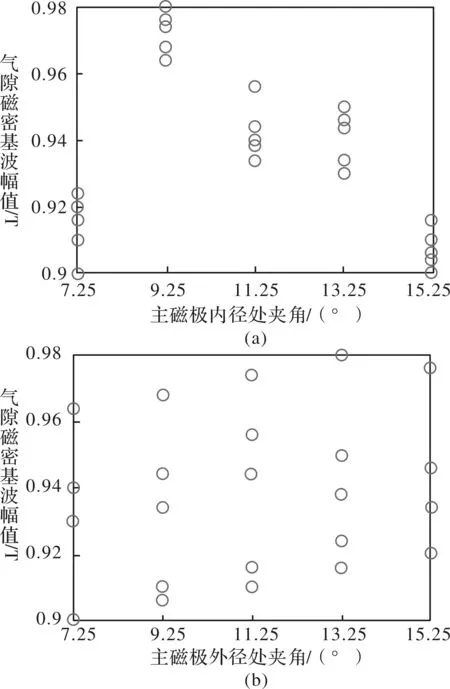
图4 气隙磁通密度基波幅值随圆心角变化曲线
从图4可以看出:当α1=9.25°且α2=13.5°时,气隙磁密基波幅值达到最大,约为0.973T。
评价函数可以很好地反映气隙磁通密度的正弦性,因此本文给出了α1和α2取不同值时评价函数F的值,如表2所示。
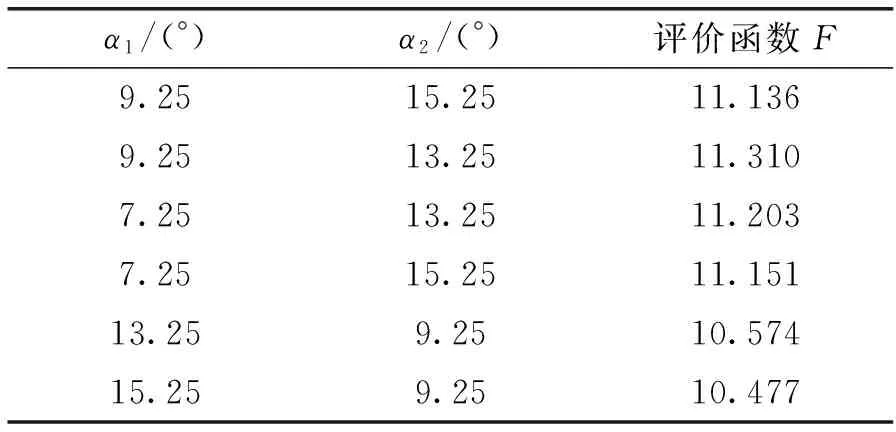
表2 α1和α2取不同值时评价函数值
由表2可以看出:当α1=9.25°且α2=13.5°时,评价函数达到最大值,说明此时气隙磁密基波幅值较大且漏磁较小。
为了进行对比分析,本文进一步仿真了传统Halbach永磁体阵列的PCB定子无铁心AFPM的气隙磁密分布。传统90°Halbach永磁体阵列磁极的内径处及外径处同圆心角相同,因此α1=α2=α,表3给出了不同α值时的评价函数值。

表3 不同α取值对应的评价函数值
由表3可知:当主磁极极角α取11.25°时,即轴向磁化永磁体极角与切向磁化永磁体极角相等时,评价函数值F即基波所占能量比最高。
当α1=9.25°且α2=13.5°时,评价函数F最大,此时电机的气隙各个位置的磁密分布如图5所示。
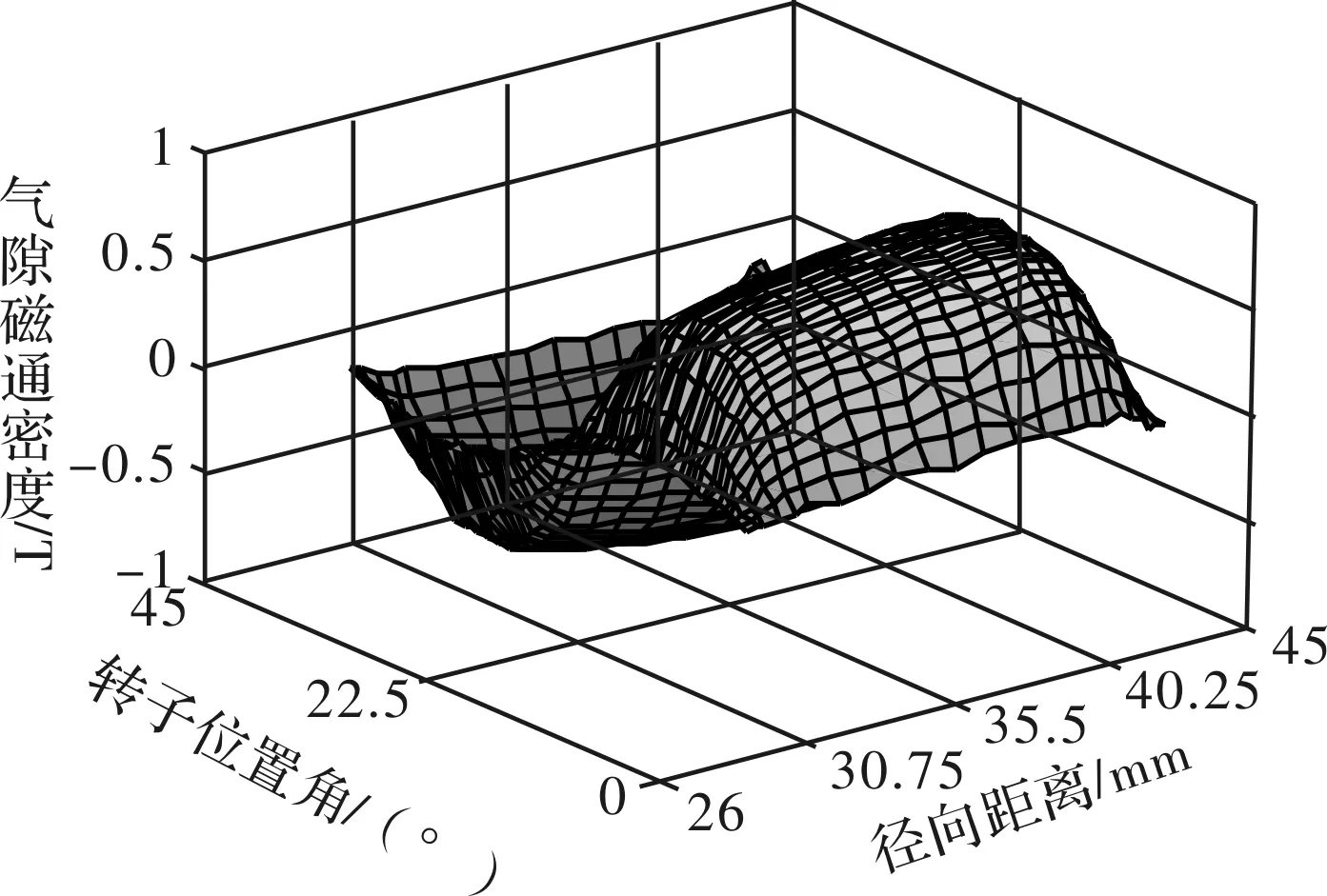
图5 气隙磁密在不同径向位置时随电角度变化曲线
图5中,θ为转子位置角,R为转子径向距离,由图5可知:气隙磁密沿半径方向呈先增大后减小的趋势,沿周向呈正弦变化的趋势。故该种情况即为本文所设计的新型Halbach永磁体阵列。此时气隙磁密的基波幅值及各次谐波幅值与传统的Halbach永磁体阵列最优结果即α1=α2=11.25°时的对比图如图6所示。
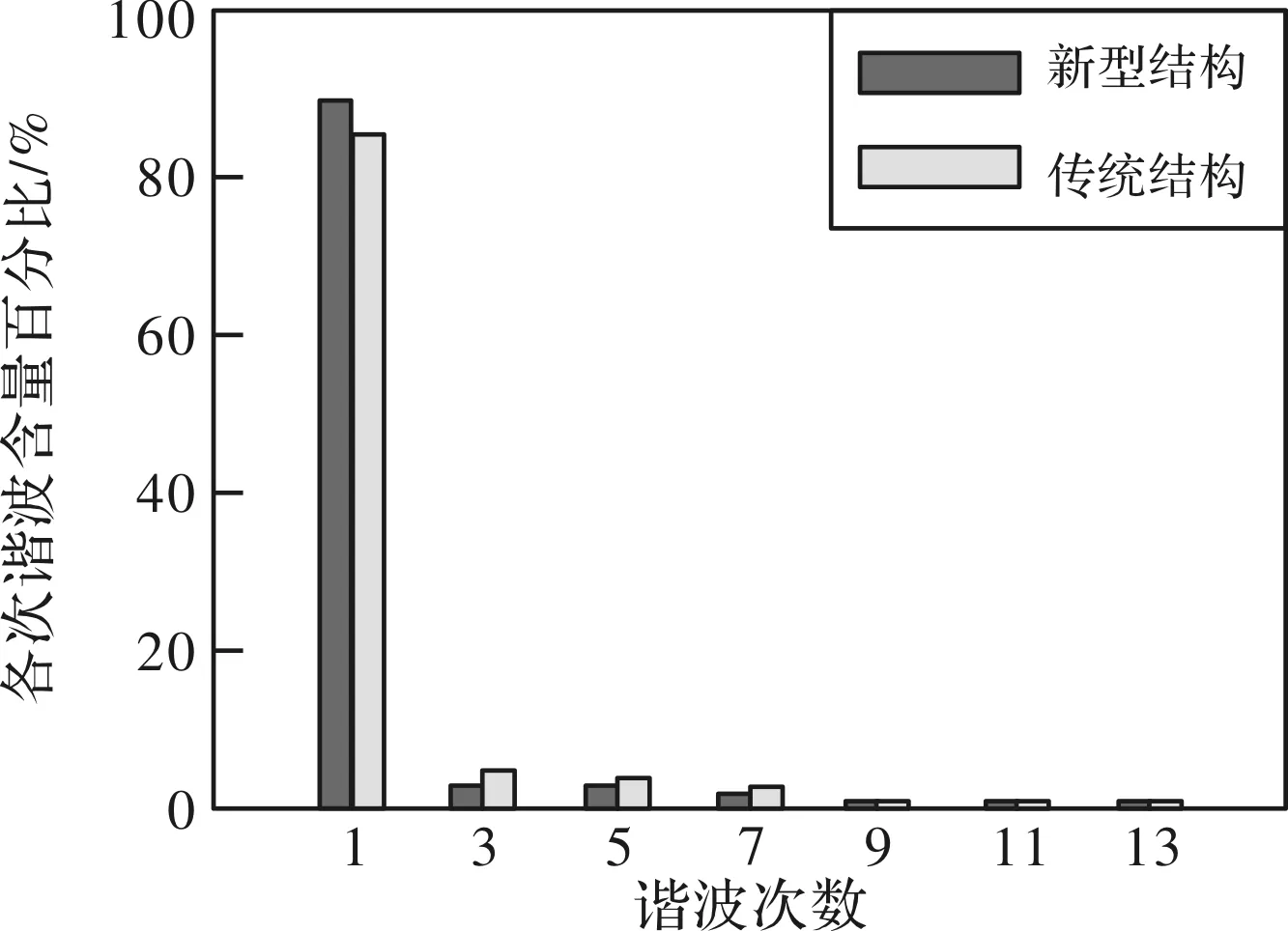
图6 基波幅值及各次谐波幅值对比图
由图6可知:该种新型Halbach永磁体阵列与传统的内外径等极角的Halbach永磁体阵列的最优结果相比,具有更大的基波幅值及更小的谐波含量。
新型Halbach永磁体阵列磁密分布云图如图7所示。
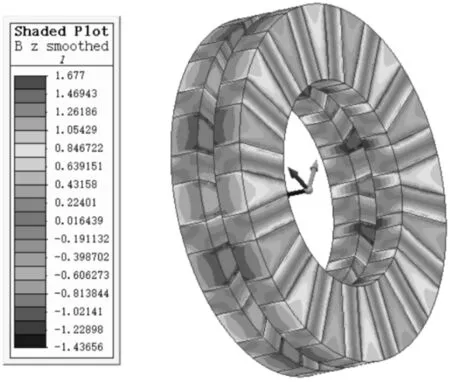
图7 新型Halbach永磁体阵列磁密分布云图
在相同永磁体用量情况下,常规轴向磁通无铁心永磁电机的磁密基波幅值仅为0.825T。由上面的仿真结果可知:PCB定子轴向磁通永磁电机用新型Halbach永磁体阵列在保证永磁体用量不变的前提下,气隙磁密的基波幅值与传统无铁心轴向盘式电机相比,上升了17.9%左右,与传统内外径等极角的Halbach永磁体阵列的最优结果相比,气隙磁密的基波幅值上升了3%左右,同时各奇次谐波的含量尤其是3次谐波的含量得到了削弱。
3.3 空载反电势仿真分析
本文对新型Halbach永磁体阵列的PCB定子无铁心AFPM和传统的PCB电机的空载反电势进行了仿真。仿真中,假设原动机在转速为500r/min的条件下拖动PCB定子永磁同步电机运行,得到电机的空载反电势波形如图8所示。由仿真波形可知:新型Halbach阵列的PCB定子无铁心AFPM反电动势的幅值为14.12V,而传统无铁心PCB电机空载反电势的幅值为12.63V,提高了11.8%左右。
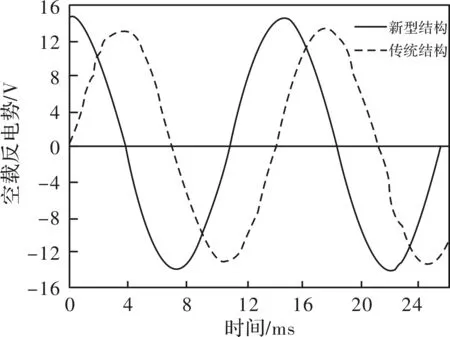
图8 空载反电势仿真图
4 样机实验
为了验证应用新型Halbach阵列的PCB定子无铁心AFPM的合理性和正确性,本文制作了样机并对电机的空载反电动势进行了验证。实验采用功率为200W的他励直流电动机作为原动机在转速为500r/min的条件下拖动PCB定子永磁同步电机运行,两者通过联轴器连接,测试实验平台如图9所示。
PCB定子轴向磁通永磁同步电机的空载反电势波形由示波器测量,实验测试结果如图10所示。由图10与图8中新型结构的仿真结果可知:实验波形和仿真波形基本呈正弦分布,且两者吻合较好。
5 结 论
本文对应用新型Halbach永磁体阵列的PCB定子无铁心轴向磁通永磁同步电机的性能进行了分析,以基波所占能量比作为评价磁钢设计是否合理的评价函数,通过改变Halbach阵列磁极的极角来调整主磁极及辅助磁极在磁钢上的分布,选出最优点,并利用有限元法仿真以及样机实验对分析结果进行验证,得出结论如下:
1)在保证永磁体用量不变的前提下,当主磁极内径与中心线的夹角α1=9.25°且外径与中心线的α2=13.5°时,气隙磁密基波幅值达到最大,约为0.973T。
2)在轴向磁化永磁体及切向磁化永磁体所占圆心角的等宽的基础上,适当增加轴向磁化永磁体在外径处所占的弧长,同时减少其在内径处所占的弧长可以有效地降低漏磁。轴向磁化永磁体在内径处减少的极角及在外径处增加的极角均为2°左右。
3)电机的仿真结果和实测结果吻合较好,因此本文建立的有限元分析计算模型以及设计方法是合理的。
