新型组合永磁偏置磁轴承磁路模型建立及优化设计

吴欣悦,徐衍亮,孙铭鑫

(山东大学 电气工程学院, 济南 250061)

0 引 言

目前，高速鼓风机、压缩机和涡轮分子真空泵等高速和高功率密度驱动器受到了广泛关注，轴承作为高速驱动设备的重要影响因素，逐渐成为了专家学者们的研究重点。与传统机械轴承相比，磁悬浮轴承具有无摩擦、寿命长、速度快、精度高等优点，更适合用于高速驱动设备。磁轴承通常分为主动磁轴承、被动磁轴承和混合磁轴承三种。由永磁体提供偏置磁场的混合型磁轴承具有功耗低、线圈数量少、结构紧凑的优势，而径向-轴向组合式混合磁轴承(Combined Radial-axial Hybrid Magnetic Bearing, CRAHMB)由于其长度短、成本低、零件数量少、功率密度高和转子动态响应更好而逐渐成为研究热点。文献[1]对于CRAHMB的拓扑结构及原理进行了介绍，并对该类磁轴承发展进行了预测，文献[2-5]对仅有一个致动目标的CRAHMB进行了磁路分析和结构设计。除了常见的CRAHMB拓扑结构，文献[6-7]介绍了两种新型结构的CRAHMB。目前CRAHMB相关论文大多为结构设计，相关的优化设计也仅仅是针对单一自由度轴承电磁力或者单个目标如功耗、体积等。文献[8-10]对于不同结构的径向磁轴承进行了结构优化设计，文献[11]对于多种拓扑结构的轴向磁轴承进行了优化设计。为获得更小的功耗文献[12]和文献[13]分别对主动型磁轴承和径向混合型磁轴承进行了能量优化。

本文首先介绍了带有两个致动目标的新型CRAHMB的结构原理，分析了补偿原理和补偿线圈设定方法。然后建立了该磁轴承的等效磁路，基于等效磁路法，对电磁力进行了解析计算，通过有限元方法仿真验证了等效磁路及电磁力解析计算的正确性，进一步阐明了该磁悬浮轴承设计的合理性。最后基于该等效磁路模型，采用多目标粒子种群算法(Multi-objective Particle Swarm Optimization, MOPSO)对该磁轴承进行了优化设计，并与初始模型进行对比，验证了优化的有效性。

1 CRAHMB的结构和工作原理

CRAHMB的结构如图1(a)所示，由径向定子、轴向定子、永磁体环、补偿线圈和转子铁心组成。径向定子由具有4个凸极的径向定子铁心及其上的径向控制线圈构成，轴向定子由截面为h形的环形轴向定子铁心及轴向环形控制线圈构成。永磁环位于径向定子和轴向定子之间，用于提供径向和轴向偏置磁通，分别如图1(b)、图1(c)中的ФRPM和ФAPM所示。缠绕在四个径向磁极上的四个径向线圈流有径向控制电流，产生如图1(b)中的径向控制磁通ФRCM，这一磁通与偏置磁通ФRPM配合，实现径向轴承的差动控制，保证径向两自由度的稳定悬浮。轴向环形控制线圈通有轴向控制电流，与补偿线圈产生的补偿磁通合成为如图1(c)所示的轴向控制磁通ФACM(具体补偿原理见下文)，这一控制磁通与径向偏置磁通ФAPM配合，实现轴向轴承的差动控制，保证轴向自由度的稳定悬浮。

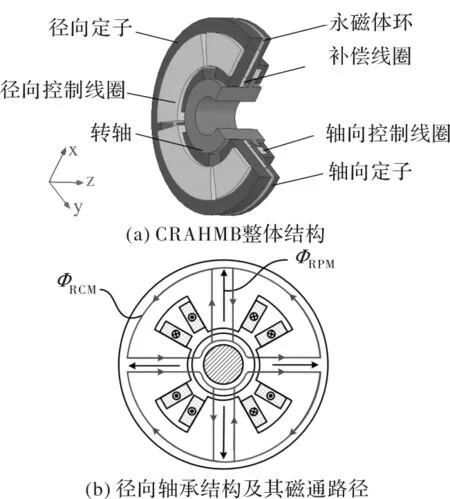
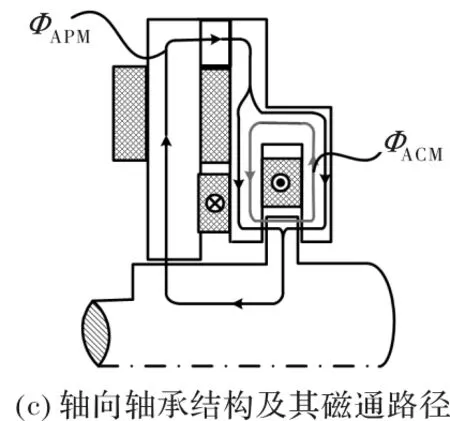
图1 CRAHMB的结构原理示意图

图2(a)为轴向控制线圈通入电流后产生的磁通，可以看出该磁通包括两部分，其一为穿过转轴推力盘、用于轴向轴承悬浮控制的控制磁通ФACM1，其二为经过径向定子铁心、只穿过一个轴向磁极面的漏磁通ФALM，这一漏磁通不但会造成径向轴承偏置磁通减小，影响径向电磁力，而且会干扰轴向轴承的稳定控制。为此在径向定子铁心与轴向定子铁心之间加一环形补偿线圈，该线圈通入电流产生的磁通如图2(b)ФBM所示，该磁通与轴向控制绕组产生的漏磁通相互抵消，轴向控制线圈和补偿线圈产生的合成磁通如图2(c)ФACM所示，有效消除了轴向控制线圈漏磁的影响。

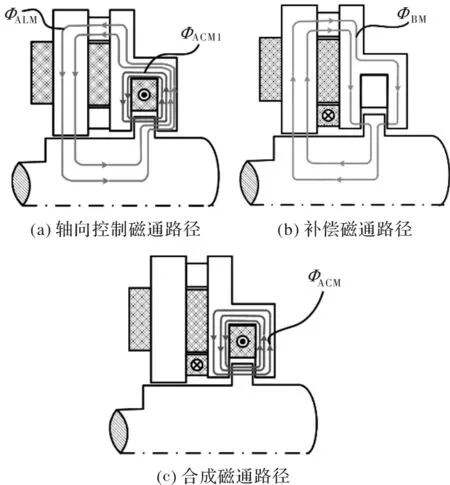
图2 补偿原理示意图

2 CRAHMB等效磁路模型的建立及电磁力计算

忽略定子和转子铁心磁阻，忽略漏磁，仅偏置磁通作用时CRAHMB整体等效磁路如图3所示，其中Fpm为永磁体磁动势，Rpm、Rx+、Rx-、Ry+、Ry-、Rz+、Rz-分别为永磁体磁阻、径向和轴向两侧气隙磁阻，Фpm、Фxm+、Фxm-、Фym+、Фym-、Фzm+、Фzm-分别为总偏置磁通、径向和轴向两侧气隙偏置磁通。

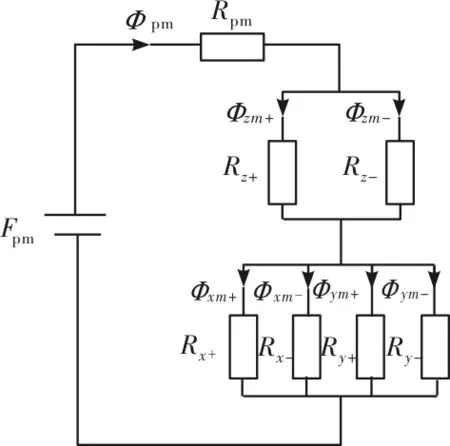
图3 仅考虑偏置磁通时CRAHMB整体等效磁路

由图3可以得到径向气隙偏置磁通Фxm+、Фxm-及轴向轴承气隙偏置磁通Фzm+、Фzm-分别表示为

(1)

图4为仅考虑控制磁通的径向轴承等效磁路，其中NxIx、NyIy为径向控制线圈产生的磁动势。

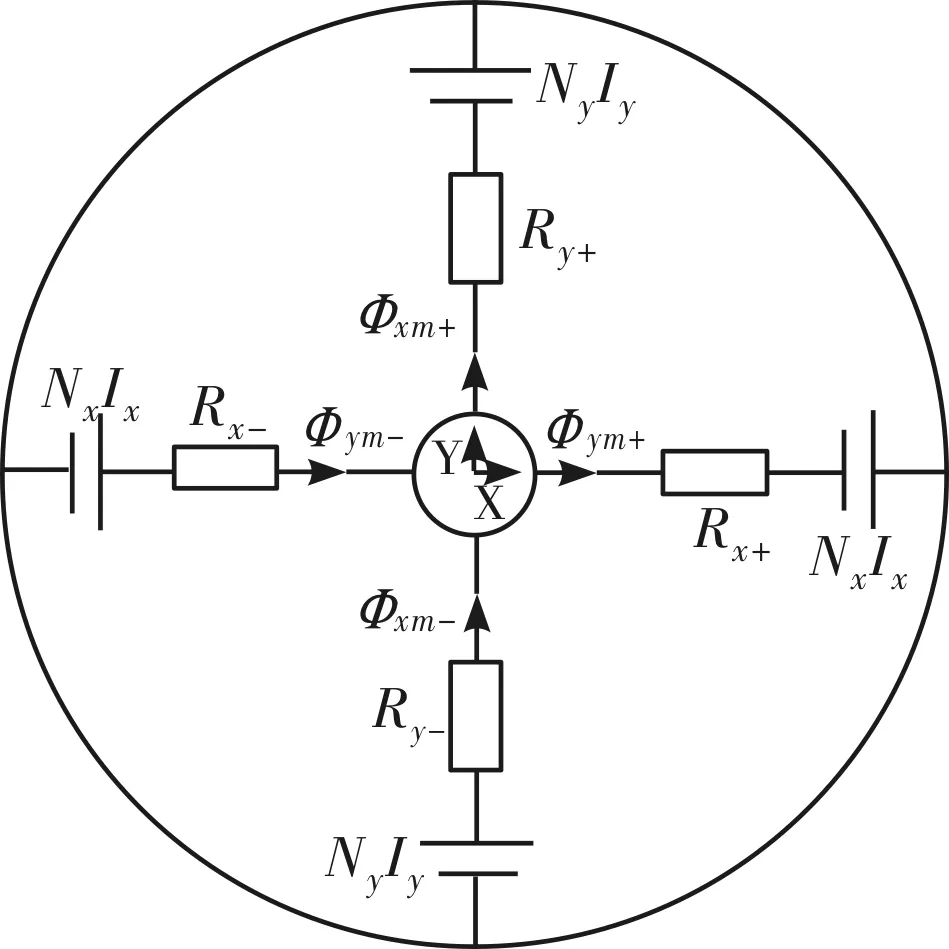
图4 仅考虑径向控制磁通时径向磁轴承等效磁路

设定图4径向磁轴承等效磁路中心节点磁势为F0, 根据基尔霍夫定律，可获得磁路方程，求出中心点磁势，进而计算出各部分径向控制磁通[14]：

(2)

即：

(3)

其中：

R=Rx+Rx-Ry++Rx+Rx-Ry-+
Rx+Ry+Ry-+Rx-Ry+Ry-

(4)

图5为仅考虑控制磁通和补偿磁通、不考虑偏置磁通的轴向轴承等效磁路，其中NzIz、NbIb分别为轴向控制线圈和补偿线圈产生的磁动势, ФZR为控制线圈和补偿线圈共同作用时径向定子的总磁通。

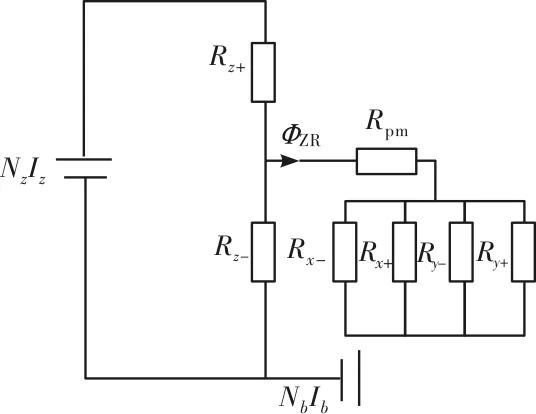
图5 仅考虑轴向控制磁通和补偿磁通时轴向磁轴承等效磁路

为了完全补偿轴向轴承控制磁通所产生漏磁的影响，轴向控制线圈和补偿线圈单独作用时产生的通过径向磁极的总磁通ФZRZ和ФZRB应大小相等、方向相反，使合成磁通ФZR为零。因此控制线圈电流Ib和补偿线圈电流Iz应满足以下关系：

(5)

其中：

(6)

由式(5)可得：

(7)

同时，由图5所示的轴向磁轴承等效磁路可得轴向控制磁通为

(8)

即：

(9)

由上述计算得到的径向、轴向两侧气隙磁通量，可以得到径向及轴向的电磁力Fx、Fz分别为[15]

(10)

当转轴位于平衡位置时，各个方向两侧气隙的磁阻相等,各方向电磁力大小为

(11)

其中：

(12)

由上述公式可知，当转轴位于平衡位置时，悬浮力与控制电流程线性关系，各个方向相互之间不存在耦合，当转轴偏离平衡位置时，轴向控制对径向没有影响，但X与Y方向会存在一定的耦合，这是大多数径向轴承固有的特性，不过在位移较小的情况下，由于气隙两侧磁阻差距不大，相应的电磁力与控制电流变化基本呈线性，对控制精度影响较小。

3 CRAHMB等效磁路模型的有限元分析验证

为验证上述CRAHMB磁路模型建立的正确性，分别采用上述建立的磁路模型和有限元仿真两种方法对该种磁轴承进行分析计算。示例轴承关键参数为表2初始值参数，根据上述补偿原理对补偿线圈进行设定。计算得到的永磁偏置磁场分布如图6所示。铁心中大部分区域的磁密小于0.8T，而靠近永磁体的局部磁密较高，达到了1.2T左右。总体而言，铁心基本未出现饱和。

图6 偏置磁通作用时径向和轴向截面磁密云图

两种方法所计算的径向和轴向的电磁力特性分别如图7和图8所示。由图7和图8可以看出：

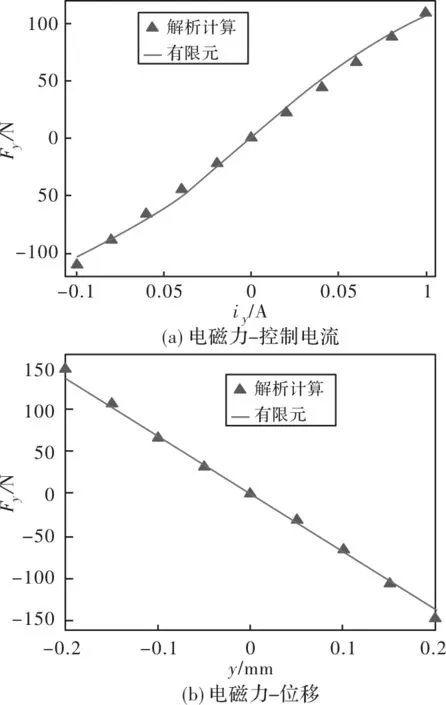
图7 径向电磁力特性

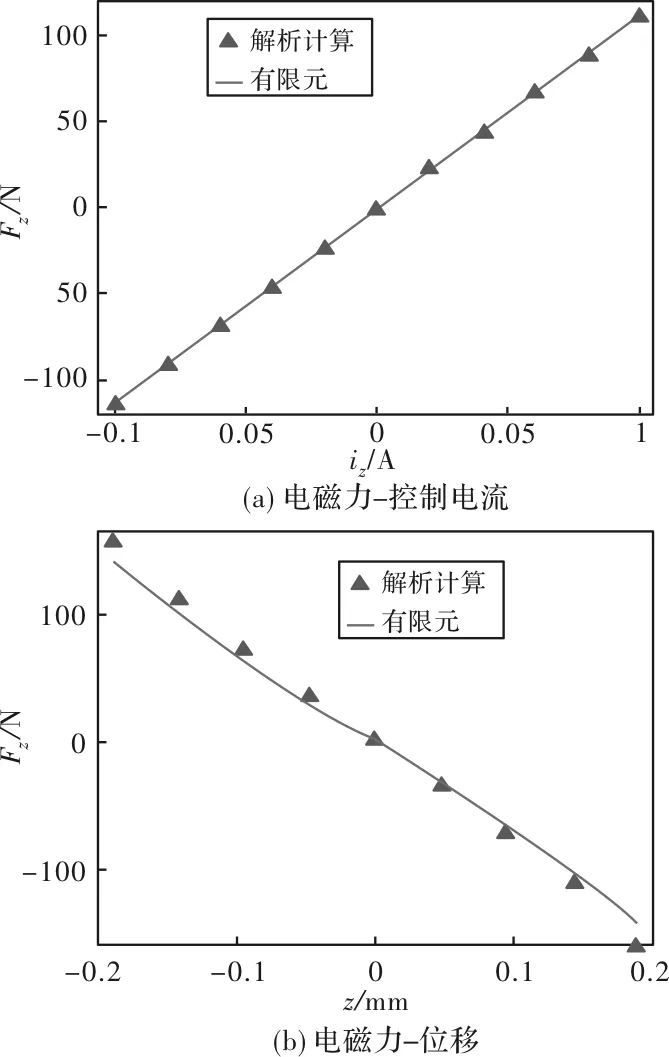
图8 轴向电磁力特性

1)磁路模型计算结果和电磁场有限元计算结果基本相符，说明了本文所建立的磁路模型的正确性，可以以该磁路模型进行磁轴承的优化设计。

2)径向轴承还是轴向轴承都具有良好的线性的电磁力特性，说明本磁轴承良好的性能及轴向控制磁通漏磁补偿的正确性。

4 基于CRAHMB磁路模型的磁轴承优化设计研究

磁轴承的体积常常受到生产成本和实际安装空间的限制，而电磁力的大小也与体积密切相关，因此对磁轴承进行径向电磁力、轴向电磁力、体积三个方面的多目标优化具有重要意义。

4.1 优化准备工作

(1)优化目标适应度函数。

径向电磁力和轴向电磁力解析表达式如式(11)所示，其中最大控制电流仍为1A。整个轴承所占体积V为所占圆筒型空间体积，即轴承最大径向面积乘以轴向总长度。

(2)选择设计变量。

磁轴承设计参数如图9所示，表1为参数与变量对应列表。

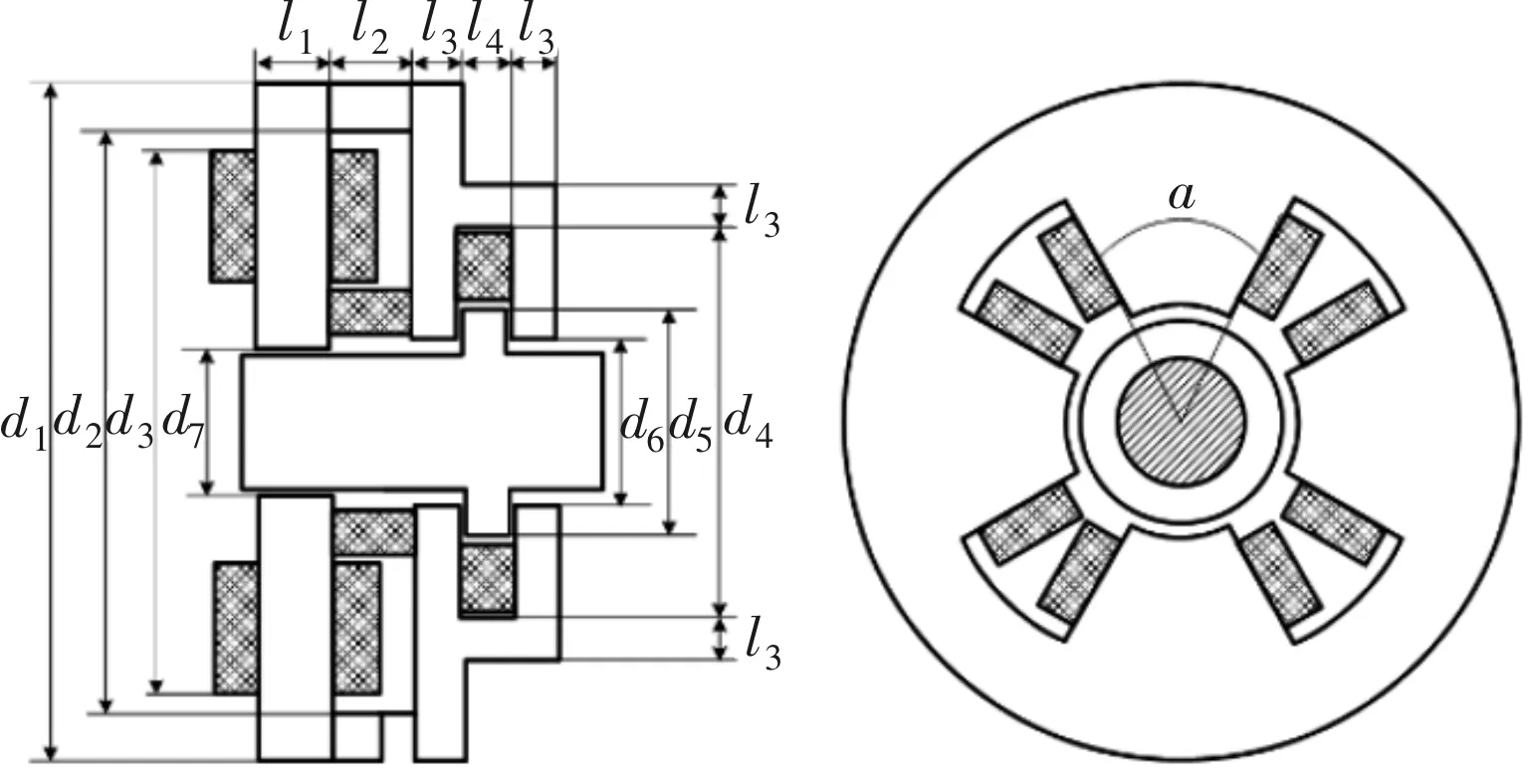
图9 CRAHMB的结构参数示意图

表1 CRAHMB结构参数与变量

其中转子铁心外径为固定值49 mm，平衡气隙厚度长度为0.5 mm，径向定子铁心内径d7为50 mm。为防止轴向磁通不经过轴向磁极，直接进入转轴，根据有限元设计经验，轴向定子内径d6固定为56 mm。由于电磁力大小只与d1、d2、l1、l2、d5、a这六个参数有关，因此为简化设计，仅对这六个参数进行优化，其他参数可根据设计经验预先确定。本次优化固定轴向定子铁心厚度l3为5 mm，l4为7 mm，推力盘厚度为6 mm，d3、d4可在设计完成后根据槽满率确定。

(3)约束

根据体积的大小要求，能够确定径向定子的外径的上限和整个磁轴承的轴向长度的上限。各个设计参数的优化取值范围可大致确定，如表2所示。

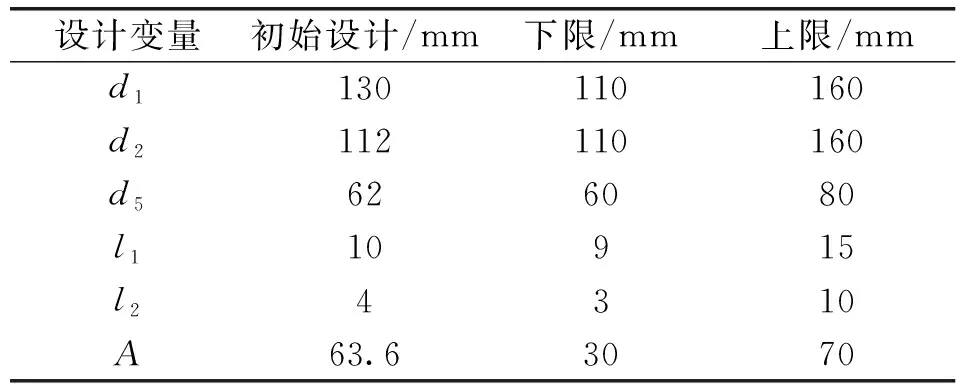
表2 设计参数初始值及范围

本文铁心材料的饱和磁密约为1.5T，考虑到安全裕度，最大密度限制在1.4T。轴承达到最大负载能力，偏置磁密和控制磁密约为0.7T。因此，磁通密度约束为

(13)

式中,Bpi和Bci分别是偏置磁密和控制磁密，i=x，y，z分别代表每个气隙。Bj为各部分铁心磁密。

槽满率约束需满足以下条件：

(14)

式中,n为控制线圈匝数，径向轴向均为160匝，dc为线圈直径0.38 mm，kc为槽满率系数0.6。

4.2 优化算法及流程

本文选用多目标粒子群优化算法进行磁轴承优化设计[16]，按照Pareto 最优原则，对径向电磁力、轴向电磁力、体积三项目标进行优化，采用精英归档策略，每个粒子的个体最优位置按照 Pareto 支配关系进行更新，所有粒子的全体最优位置从档案库中选取。该方法不需要加权权重，可以获得大量优质的非劣解，决策者可以根据具体需求选取符合要求的满意解，大大简便优化设计时间。该MOPSO 法中，群体规模为50，最大迭代次数为100，惯性权重从 1.2 到 0.1 线性递减，加速因子c1= 2，c2=2。采用 Matlab 进行编程仿真。优化算法流程如下所示[17]:

Step1: 初始化种群。给定多目标粒子群算法的控制参数、迭代次数、群体规模，初始化粒子位置和速度，设定初始位置为最初的个体历史最佳位置，计算初始粒子的适应度值。

Step2：初始筛选非劣解集。在满足所有约束的前提下，根据Pareto最优概念从初始粒子种群中筛选出非劣解集。

Step3：更新粒子速度和位置和迭代次数。根据个体的历史最佳位置、惯性因子和学习因子，更新粒子速度和位置。每更新一次粒子，迭代次数加1。

Step4：更新个体历史最佳位置。根据Pareto最优概念，判断更新前粒子是否受到当前粒子支配，若受支配，则更改当前粒子位置为个体最佳历史位置，若不受支配，则在两者之间随机选择。

Step5:更新非劣解集。在满足约束前提下，从当前粒子中筛选非劣解加入到非劣解集中，并将其中重复粒子剔除。

Step6：判断是否达到最大迭代次数，若达到迭代次数，则输出此时非劣解集及其适应度值；否则返回Step3。

4.3 优化结果分析

图10、图11给出了MOPSO算法获得的径向电磁力和轴向电磁力关于体积的Pareto最优解前端，即非劣解集。其中每个粒子都是所占体积值下能获得最大电磁力的最优方案。选择其中较有代表性的方案1和方案2与初始方案对比，对比详细情况如表3所示。

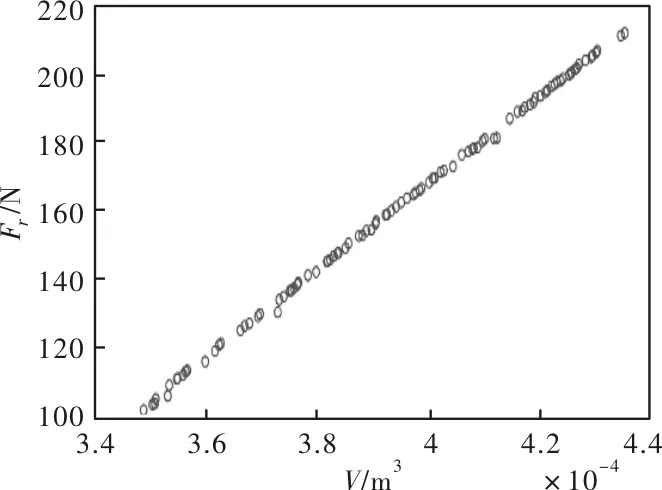
图10 径向电磁力的Pareto最优解前端

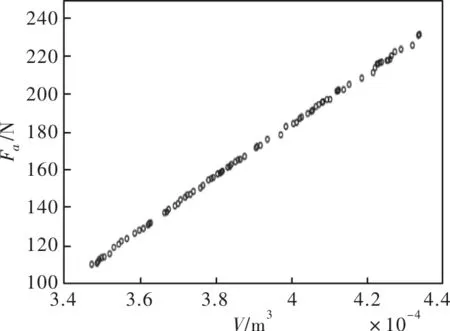
图11 轴向电磁力的Pareto最优解前端

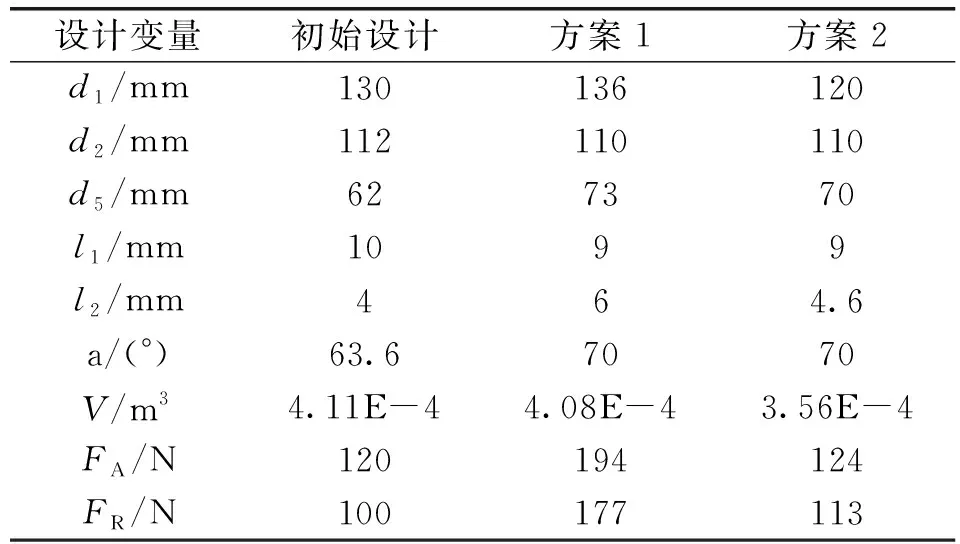
表3 MOPSO优化结果分析

由表3可以看出，方案1与初始方案体积相同，但是电磁力却远高于初始方案，其中轴向电磁力提高61.6%，径向电磁力提高77%。方案2与初始方案的轴向电磁力大致相同，但体积却减少了13%，径向电磁力也略高于初始方案。以上的方案对比证明了优化的有效性，大大提高了设计效率。

5 结 论

本文研究了一种新型结构的径向-轴向组合式混合磁悬浮轴承，对于该磁轴承的结构和工作原理进行了详细的阐述。由于轴向控制磁通漏磁会对径向和轴向控制的产生影响，选择采用补偿线圈对漏磁通进行补偿，分析了补偿原理和补偿线圈设定方法，建立了整个轴承的磁路模型，并基于该磁路模型对电磁力进行了解析计算。以初始模型为例，通过有限元仿真验证了磁路模型的准确性和补偿线圈设定的合理性。

本文将磁轴承轴向电磁力及径向电磁力、体积作为优化目标，采用多目标粒子种群优化算法对轴承的主要设计参数进行优化，得到了一系列非劣解。选择其中具有代表性的优化方案与初始方案对比，均获得了较好的优化效果，为该类磁轴承的优化设计与分析提供了新思路。