直流偏磁情况下的定子永磁电机铁耗计算

程 明，李 彪，王景霞

(1.东南大学 电气工程学院，南京 210096;2.国网徐州供电公司，江苏 徐州 221005)

0 引 言

随着永磁材料和电力电子技术的迅猛发展，定子永磁电机得到日益广泛的关注。与传统转子永磁电机不同，定子永磁电机将永磁体固定在定子上，极大简化了转子结构，排除了由于高速旋转而产生的离心力所带来的隐患；同时，永磁体安装在定子，有利于电机的散热，降低了永磁体发生不可逆退磁的几率[1]。但是，由于永磁体安装在定子上，定子铁心不可避免地受到直流偏磁的影响，且由于定子槽的存在，导致定转子铁心中磁密波形发生不同的偏磁现象[2]，这时采用传统的损耗模型计算磁滞损耗将产生较大误差。

近年来，有许多学者开始研究直流偏磁对电机铁耗的影响。文献[3]指出直流偏磁影响的主要是磁滞损耗，且随着频率和交流磁密幅值的增加，其影响越小。文献[4]虽然没有提及直流偏磁，但其提出的分段式模型对准确计算电机铁耗有较大意义。文献[5]提出了SPG模型，该模型在纯正弦激励情况下考虑了磁路饱和的情况，计算精度相对较高。文献[6]提出了一种简单通用的硅钢片铁耗预测方法，该方法可以计及直流偏磁的影响且不用进行大量实验。文献[7]提出了一种基于斯坦梅茨方程的磁滞损耗改进模型，该模型同时考虑了直流偏磁Bdc和磁密幅值Bm对磁滞损耗的影响，且给出了一个适用范围较大的计算模型；文献[8]在前者的基础上对铁耗模型进行了改进，所得模型在偏磁小于0.6T时取得了更好的拟合效果，进一步提高了偏磁情况下铁耗计算模型的准确度。对于上述两个模型，虽然很好地描述了直流偏磁与磁滞损耗之间的关系，但是这两种模型的系数是在多种交流磁密幅值情况下对所有数据进行拟合得到的，因此并不能达到精细化的铁耗计算。

本文以一台双凸极定子永磁电机为例，研究分析了定子永磁电机内部存在的直流偏磁现象。然后利用爱泼斯坦方圈进行偏磁铁耗实验，基于实验数据和传统偏磁铁耗模型提出了一种考虑磁密幅值的偏磁铁耗计算模型，将该模型应用于二维有限元分析软件，对双凸极定子永磁电机进行铁耗计算，并与传统模型进行了对比。最后，对该电机进行了铁损实验，进一步验证了模型的准确性。

1 定子永磁电机磁密波形特点

图1为一台双凸极定子永磁电机的二维模型，对该电机进行有限元电磁场分析。图2给出本电机所用硅钢片发生直流偏磁时的小磁滞回环。其中，Bm为一定的交流励磁电压下没有直流偏磁时测得的交流磁密幅值，Bm_dc为在同样的交流励磁电压情况下存在直流偏磁时测得的交流磁密幅值，Bdc为直流偏磁量。分别选取定子和转子上一点，画出磁密波形如图3所示，其中图3(a)为定子齿A点磁密波形，图3(b)为转子齿B点磁密波形，可以发现其磁密波形均发生了直流偏磁现象。直流偏磁对电机磁滞损耗产生影响，使温升增高，影响电机性能甚至损坏电机；因此在对定子永磁电机进行铁耗计算时，需要充分考虑直流偏磁带来的影响。

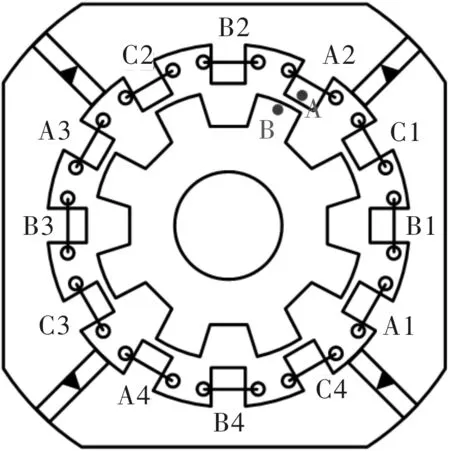
图1 双凸极定子永磁电机二维有限元模型

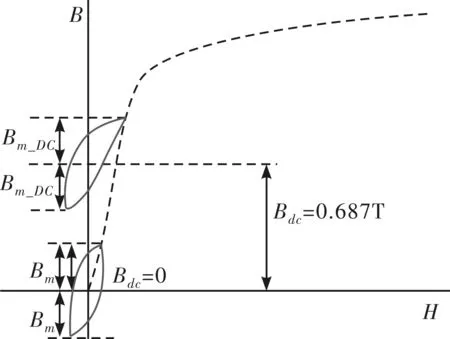
图2 直流偏磁情况下的小磁滞回环

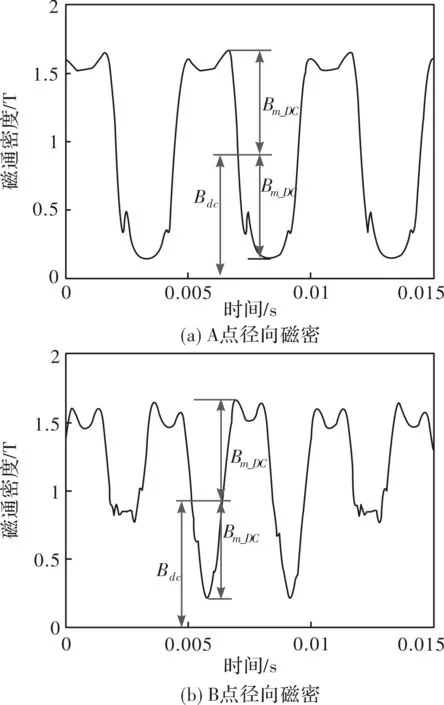
图3 定转子径向磁密波形

2 传统铁耗模型

2.1 传统铁耗模型介绍

当正弦电流供电时，Bertotti提出的经典铁耗模型得到了广泛的应用，其模型可表示为[9]

PBertotti=Ph+Pe+Pa
=khfBα+kef2B2+kaf1.5B1.5

(1)

式中，Ph、Pe和Pa分别表示磁滞损耗，涡流损耗和附加损耗，kh、ke，α，和kα为相应分量损耗的常系数，通常情况下α取2。

式(1)将铁耗分为三项式，在不同频率以及磁密幅值的情况下拟合求得相关系数，但是该模型并无法考虑直流偏磁对硅钢片损耗的影响，因此有学者提出了具有代表性的偏磁损耗模型1[7]：

Ph=f1(Bdc)·Ph0

(2)

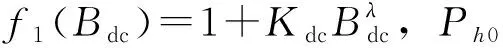
文献[8]将Bertotti模型简化成两系数的两项式，并在式(2)的基础上，添加了二次项，实现了对偏磁小于0.6T的细化拟合，改进后得到的偏磁模型2如下：

Ph=f2(Bdc)·Ph0

(3)

2.2 传统铁耗模型存在的问题

偏磁模型2虽然较好的描述了直流偏磁与铁耗的关系，但是该模型是在不同交流磁密幅值情况下拟合得到的，如图4所示，针对6种不同交流磁密幅值情况下进行的偏磁铁耗实验数据，进行处理并拟合，得到偏磁模型2拟合曲线；由图可以看出偏磁模型2的拟合曲线与实验结果在整体上取得了较好的吻合，然而在局部上存在一定误差，例如Bdc=0.8T时，Bm=0.5T对应的偏磁实验数据处理结果为1.21，Bm=0.6T对应的偏磁实验数据处理结果为1.75，然而偏磁模型2默认两种不同磁通密度幅值情况下的结果均为1.38。

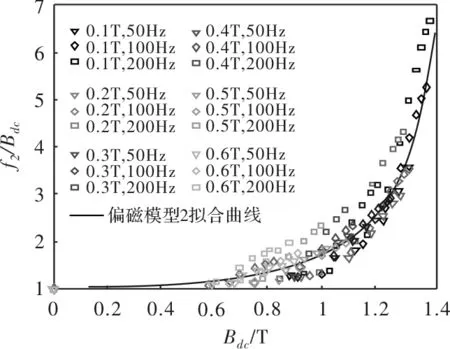
图4 偏磁模型2拟合情况

3 直流偏磁情况下的铁耗研究

3.1 无偏磁铁损系数

为了解决传统偏磁模型存在的问题，需要在不同磁通密度幅值的情况下，研究直流偏磁对铁耗带来的影响；进一步地，需要先获取无偏磁正弦交流供电情况下，硅钢片的Bertotti模型系数。

在工程应用中，式(1)的第三项即附加损耗非常小，因此常将其忽略，进而将式(1)简化为

Ph0=khfBα+kef2B2

(4)

利用爱泼斯坦方圈对硅钢片进行铁耗实验，实验装置如图5所示，实验对象为武钢生产的35WW250冷轧无取向硅钢片。在4组不同频率工况下，进行若干组纯交流铁耗实验，根据式(4)进行拟合，即可得到无偏磁铁损系数，拟合结果如表1所示，拟合情况如图6所示。实验铁耗计算公式为[8]

(5)

式中，PFe_exp为无偏磁时测量铁耗。i(t)为爱泼斯坦方圈励磁绕组侧的测量电流，e2(t)为测量绕组测的测量电压，T为一个周期的时间长度。

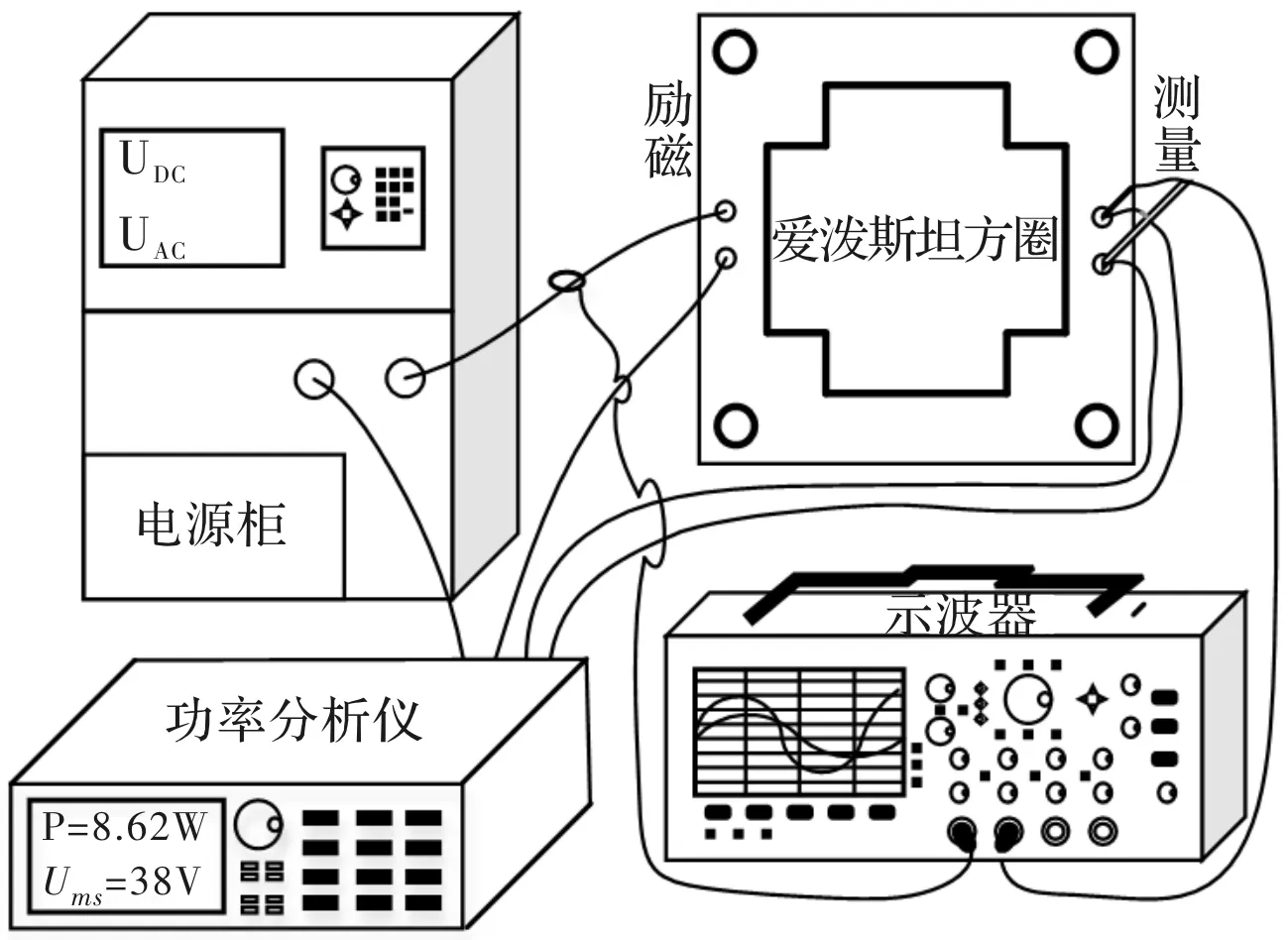
图5 直流偏磁实验装置示意图

表1 35WW250 Bertotti模型系数

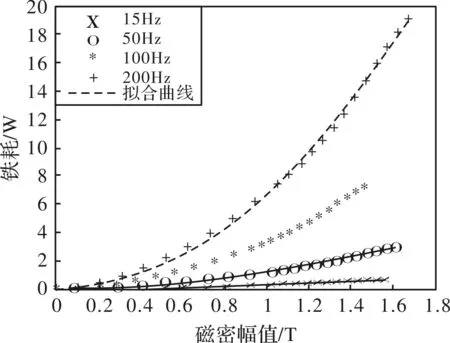
图6 低频无偏磁拟合的Bm-P0曲线

3.2 偏磁铁耗实验及数据处理

利用图5所示装置进行直流偏磁铁耗实验，与无偏磁铁耗实验不同的是，交流电源输出的是带有直流分量的电压，本文共进行了约440组偏磁铁耗实验，具体实验工况如表2所示。

表2 偏磁实验测量范围

将计算得到的无偏磁正弦交流供电下铁损系数带入式(4)可得到传统无偏磁铁耗模型为

wFe=135.65fBα+1.2507f2B2

(6)

根据式(6)分离出正弦情况下的涡流损耗和磁滞损耗计算公式可分别表示为

Peddy_sin=1.2507f2B2

(7)

Phys_sin=135.65fBα

(8)

研究表明，当存在直流偏磁时，绕组上的压降要大于同等交流励磁电压时不含直流偏磁的情况。因此，对于无偏磁和有偏磁两种情况下的铁耗实验，在这两种情况下，即使确保绕组中的交流激磁电压相同，前者的交流磁密幅值仍然会略高于后者[10]。另外，当发生直流偏磁时，式(5)中的e2(t)仅存交流分量，不能直接计算直流偏磁下的铁耗。因此，需要使用以下计算公式对偏磁情况下的铁耗测量值进行修正：

(9)

式中，PFe为与磁密幅值Bm同等的交流电压励磁下直流偏磁时修正后的铁耗测量值。

最后，联合式(8)和式(9)可得到磁滞损耗的测量值：

Phys_DC=PFe-Peddy_sin

(10)

此外，值得注意的是，直流偏磁在方圈中产生恒定磁场，但在方圈二次侧绕组中并不产生感应电势，因此直流偏磁Bdc并不能直接通过二次侧电压得到，通常要通过图7所示工程方法获得Bdc的大小。

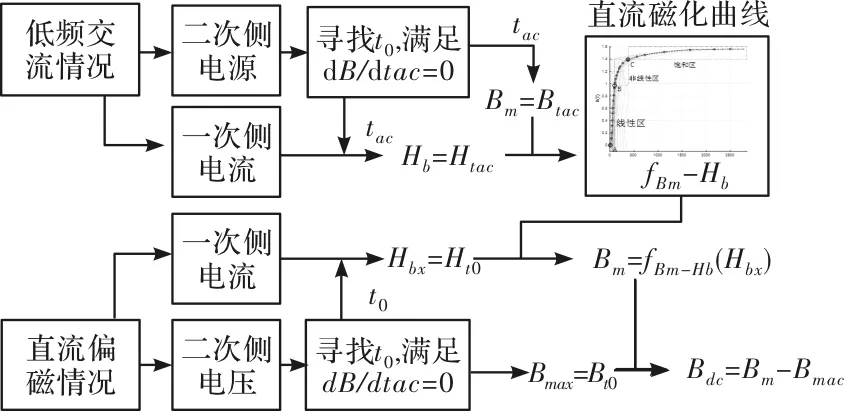
图7 Bdc计算过程示意图

3.3 传统偏磁模型的拟合

最终综合利用式(10)推导得到的偏磁铁耗测量值Phys_DC以及式(8)分离得到的铁耗计算值，在不同磁通密度幅值情况下，分别按照式(3)进行拟合。从Bm=0.1T工况开始拟合，当拟合到Bm=0.5T工况时，发现不同工况下拟合得到系数λ和Kl相差不大，而Kdc相差较大，拟合结果如图8所示。

由此取λ和Kl为固定值，本文取值如下：

(11)

将式(11)代入式(3)，重新拟合，得到0.1T～1T共10组数据的拟合结果如表3所示，拟合效果如图9所示。

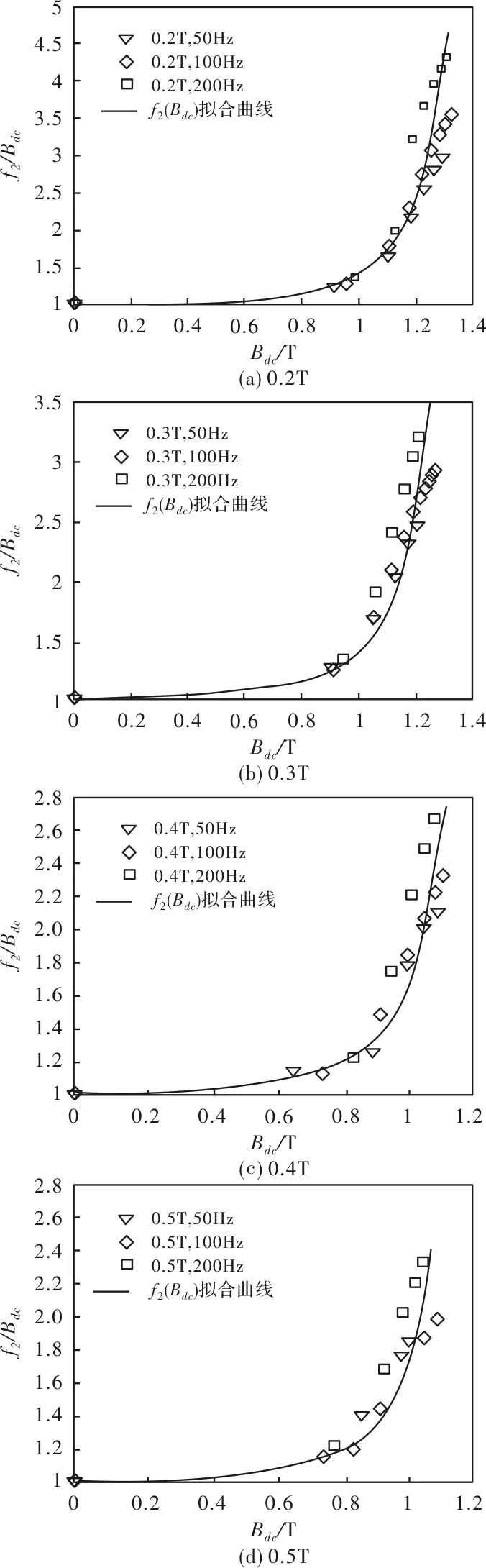
图8 不同磁密幅值情况下偏磁模型2的拟合

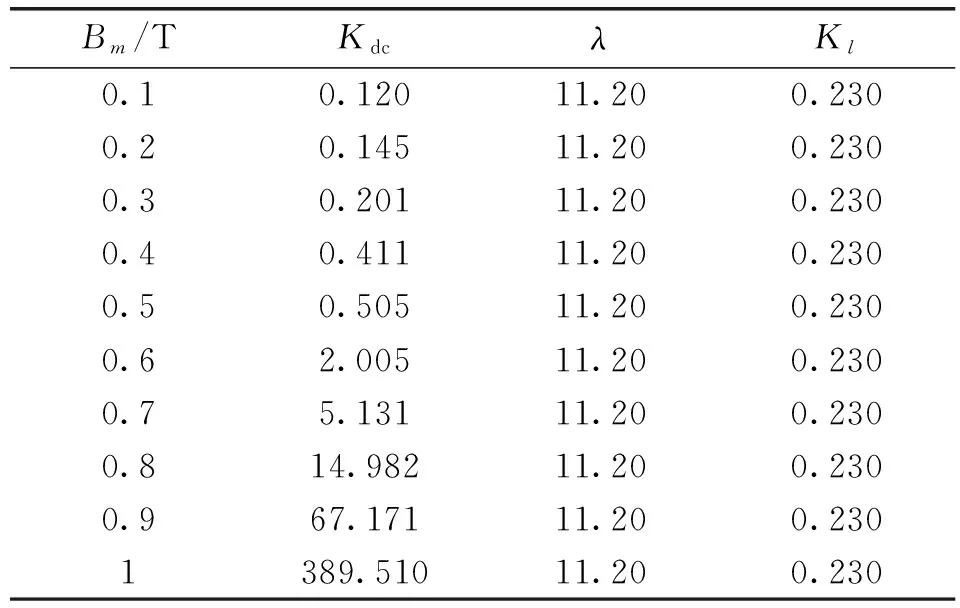
表3 0.1T至1T偏磁数据重新拟合结果

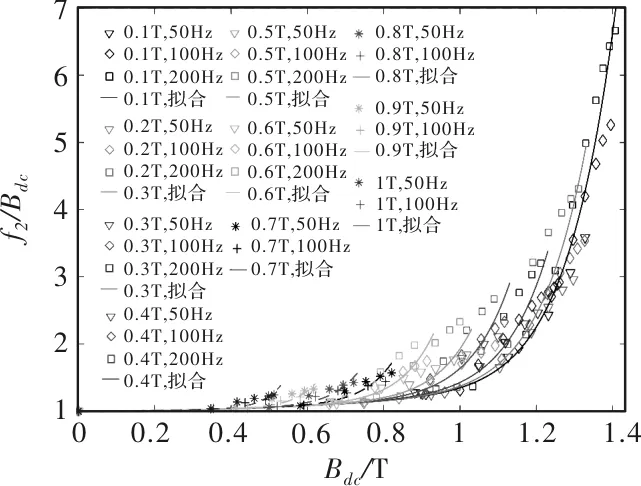
图9 所有偏磁数据的拟合结果

3.4 改进模型的提出

在表3的基础上，进一步研究偏磁模型中的系数Kdc与磁密幅值Bm的定量关系。由于表3中的Kdc数值差别较大，因此需要对Kdc做如下处理：

r=ln(Kdc)

(12)

式中，r为偏磁系数Kdc的自然对数，无任何意义，仅为方便拟合。处理后得到的数据与磁密幅值Bm的关系如图10所示，发现r与Bm之间可用如下函数描述：

(13)

式中，a、b、c均为常系数。

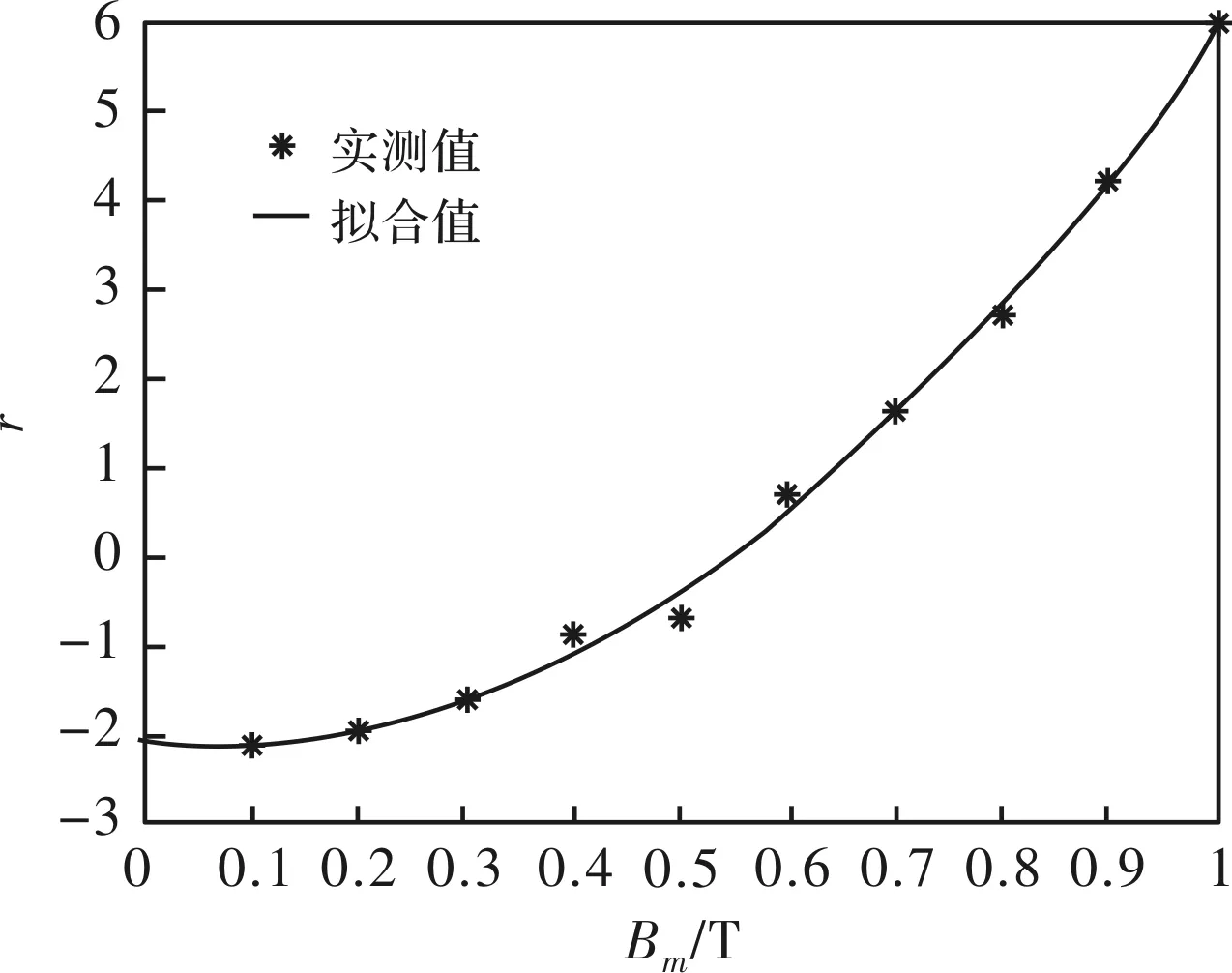
图10 归一化系数r与Bm关系曲线

在Matlab中对r与Bm按照式(13)进行拟合，得到拟合结果如表4所示，拟合多重测定系数R-square为0.9972，接近于1，表明拟合程度较好。

表4 改进模型系数

联合式(3)、式(10)至式(13)，并结合表4，最终得到改进后的偏磁模型为

(14)

4 电机的铁耗计算

在空载、1000 r/min工况下，采用不同模型对一台12/8极双凸极定子永磁电机进行铁耗计算，结果如表5所示，图11为一个周期内磁滞损耗随仿真时间变化的情况。由表可知，偏磁模型2与本文提出的模型由于考虑了直流偏磁情况，磁滞损耗相对传统铁耗模型分别增加了16.8%和17.6%。本文提出的模型磁滞损耗计算结果较偏磁模型2增加了0.69%，这是由于本文模型的系数综合考虑到直流偏磁大小以及磁密幅值大小所带来的影响，因此在计算磁滞损耗时，对于幅值不同的磁密波形，计算系数随之改变，因此模型的相对精度进一步提高。

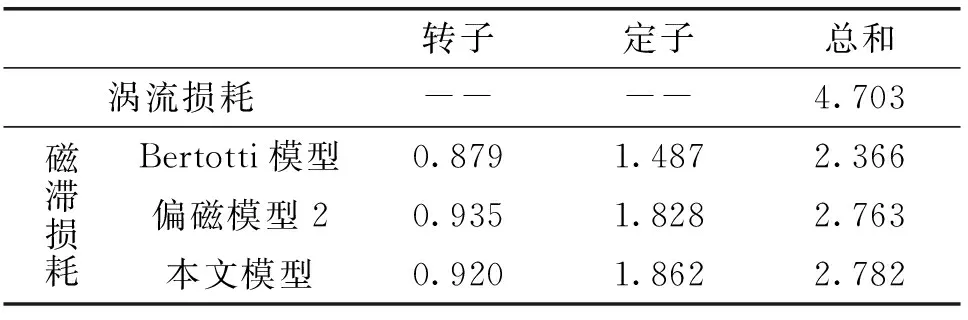
表5 DSPM铁耗计算结果

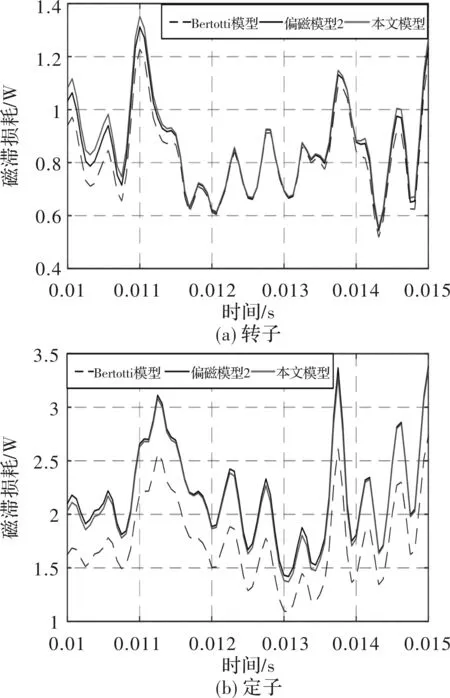
图11 双凸极定子永磁电机动态磁滞损耗对比图

5 实验验证

最后对这台12/8极双凸极定子永磁电机进行了空载损耗实验。在电机运行过程中存在铜耗、铁心损耗(包含硅钢片磁滞损耗和涡流损耗、永磁体涡流损耗、附加损耗等)、机械损耗、风磨损耗。电机空载时，绕组没有电流因而不存在铜耗；对于12/8极DSPM电机，在转子旋转过程中，永磁磁通所经磁路的磁阻可以认为恒定不变，因而永磁体的工作点基本不发生变化，因此可以认为永磁体涡流损耗几乎为零。DSPM电机的机械损耗以及风磨损耗通过一台相同尺寸的电励磁双凸极电机测量得到，实验时通过一台直流电机拖动该DSPM电机旋转，直流电机输出功率即为DSPM电机的铁耗及机械损耗和风磨损耗之和，因此DSPM电机的铁耗可由直流电机输出功率与机械损耗以及风磨损耗做差得到。

在不同转速情况下得到实验与模型计算结果的对比如图12所示。对比计算结果与实验结果可以发现，不同转速情况下，本文偏磁模型计算铁耗高于偏磁模型2计算铁耗，又高于传统铁耗模型计算铁耗；本文偏磁模型计算铁耗与铁耗实验结果吻合度较高。

图12 动态磁滞损耗对比图

6 结 论

本文从直流偏磁的角度出发，对双凸极定子永磁电机进行了铁耗计算。通过爱泼斯坦方圈对35WW250钢片进行直流偏磁实验，基于测量数据结果，提出了考虑磁密幅值的偏磁铁耗计算模型。总结如下：

1)定子永磁电机内部存在直流偏磁现象，直流偏磁现象会导致铁耗增加。

2)不同磁密幅值情况下磁滞损耗与偏磁大小的变化规律相似但有所不同，基于该规律本文提出一种考虑磁密幅值大小的偏磁铁耗计算模型。

3)本文提出的模型适用于存在直流偏磁现象的电机尤其是定子永磁电机，该模型能够反应不同磁密幅值情况下，偏磁对铁耗所带来的影响，其计算结果较未考虑偏磁的模型增加17.6%。此外，通过对双凸极定子永磁电机进行的空载损耗实验，进一步验证了模型的准确性。