基于SVPWM的时间谐波对永磁电机损耗的影响

2020-04-20韩雪岩郭谨博李宏浩朱龙飞

微电机 2020年11期

韩雪岩，郭谨博，李宏浩，朱龙飞

(沈阳工业大学国家稀土永磁电机工程技术研究中心，沈阳 110870)

0 引言

随着电力电子技术的发展，变频器被越来越多应用于永磁电机控制领域，使其具有更宽的调速范围，为电机稳定可靠运行提供便利[1]。但变频器的使用引入大量的电流时间谐波，该谐波磁场在电机中高速旋转，产生过热的温升，因此准确计算时间谐波引起电机损耗的大小及分布具有积极意义。

当今变频器采用较多的调制方式是：空间矢量脉宽调制Space Vector Pulse Width Modulation(SVPWM)技术，通过变频器不同开关模式的组合，形成空间电压矢量得到圆形空间磁链矢量，在电机内产生圆形旋转磁场[2]。变频器供电时，由于电压电流波形非正弦而产生谐波称为电流时间谐波，而产生的损耗为附加谐波损耗，其分别附加在定子绕组铜耗，基波铁耗，永磁体涡流损耗，周围结构件涡流损耗[3,4]。

国内外已有许多人对变频器供电引起的时间谐波造成的电机损耗进行了研究，并取得一定成果。文献[4,5]研究表贴式永磁电机在不同变频器参数、气隙长度和转子磁路结构时，以及不同供电方式下电机各部位附加损耗变化规律。文献[6]在变频器供电下，分析两种不同转子磁极结构的内置式永磁电机的损耗和温升分布规律。文献[7]从铁心材料方面研究非晶合金与硅钢片电机的谐波损耗。文献[8]提出一种时域与频域有限元相结合的方法，对变频器载波在永磁电机中产生的谐波损耗进行快速的计算。文献[9]提出一种在每个转子的形状上进行电磁场和电枢电压方程耦合的分析方法，对转子永磁体位置、隔磁桥形状进行优化。文献[10]对电机的磁场谐波含量进行研究，提出了一个确定电机的时间和空间谐波成分的简单方法。文献[11-12]利用电磁场与温度场耦合方法，研究电压谐波造成的电机损耗与温升影响和变化规律。

本文以表贴式永磁同步电机为例，并为更好体现SVPWM的优势，引入正弦脉宽调制Sinusoidal Pulse Width Modulation(SPWM)技术相对比，利用傅里叶分析两种方式下电流各次谐波大小及分布，并分析调制比、载波比对电流谐波的影响；运用时步有限元法，研究永磁电机的定转子铁心损耗、永磁体涡流损耗、绕组铜耗、周围金属构件涡流损耗的大小和分布规律；参考IEC60034-2-3:2013电机损耗和效率确定的试验方法搭建测试平台，校核有限元计算的损耗结果与试验结果。

1 SVPWM原理及模型

1.1 SVPWM算法原理

SVPWM是基于空间电压矢量合成的PWM如图1所示，六个非零电压矢量将圆形平面分成六个扇区，任一扇区的电压矢量由其相邻两个非零矢量以及零矢量通过通断时间不同组合而成，合成电压矢量匀速旋转，形成圆形的空间电压矢量，通过控制变频器开关状态产生的实际磁通近似圆形磁链。

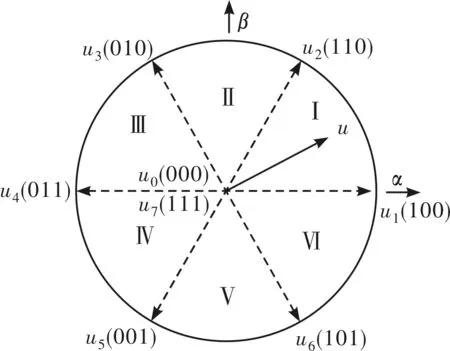
图1 SVPWM扇区与电压矢量图

SVPWM的调制波呈马鞍形，触发脉冲的生成原理如图2所示。

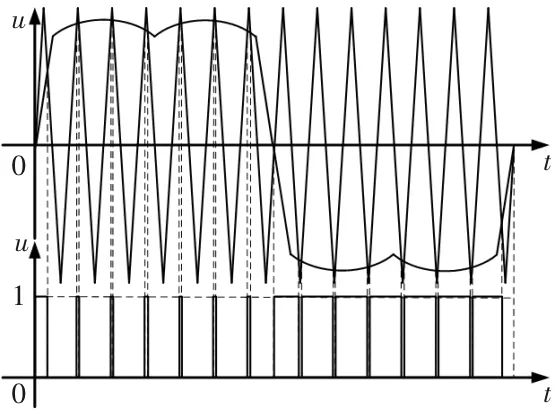
图2 SVPWM脉冲生成原理

在脉冲宽度调制过程中引入两个关键参数，三角载波频率fc与调制波频率fr之比，称为载波比N。

N=fc/fr

(1)

调制波幅值ur与三角载波幅值uc之比，称为调制比M。

M=ur/uc

(2)

1.2 仿真模型搭建

变频器主电路如图3所示，SVPWM产生的触发脉冲对主电路三个桥臂上的六个IGBT开关管的控制，能量从左边的直流源，经过中间的三相桥式PWM逆变电路，到右边永磁电机驱动所需的三相电压电流。其中PWM变频器是产生时间谐波的来源，电流谐波幅值与谐波丰富程度会直接影响永磁电机损耗。

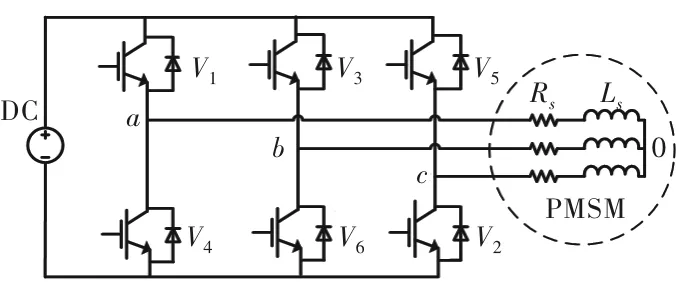
图3 PMSM-PWM变频器主电路结构图

基于Simulink搭建的SVPWM触发电路如图4所示。

在数据信息获取方面，本文主要通过公开的互联网渠道、各企业官网、新闻纪录等渠道，获取有效信息，同时辅助以前人的文献研究，对各企业商业模式进行归纳总结。

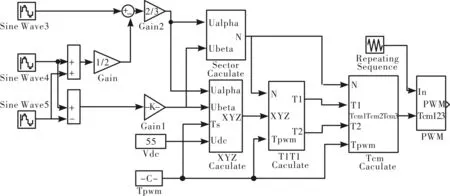
图4 SVPWM触发模拟电路

任何周期信号都能够由不同谐波的正弦波叠加而成，利用傅里叶级数分析电流波形的正弦型，以及研究各次电流时间谐波的影响情况。

(3)

为了反映波形的畸变程度，引入总谐波畸变率THD表示，定义如下：

(4)

式中,In为第n次谐波电流有效值；I1为基波电流有效值。

2 电流时间谐波变化及分布规律

引入SPWM方式与SVPWM相比较分析得出，SVPWM的电流谐波畸变率比SPWM低1%至2%，而电流基波幅值比SPWM高5A左右；研究载波比、调制比对SVPWM产生的谐波分布规律。

2.1 载波比与THD、基波电流幅值关系

从图5中分析得出，随着载波比的增加，THD呈减小趋势，而减小的速率在载波比N=15出现拐点，拐点前下降速率较快，拐点后下降速率变缓。

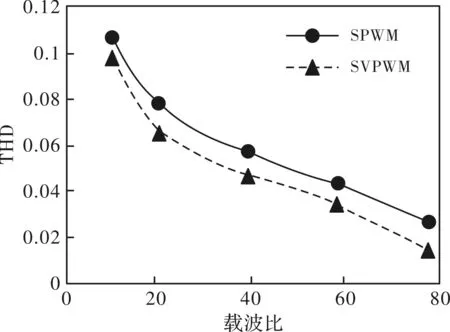
图5 M=0.6下，N与THD关系

从图6中看出电流基波幅值基本不随载波比变化。随着载波比的增加会导致开关器件的损耗增加，因此根据需要选用合适的载波比来平衡畸变率与开关损耗间的关系。

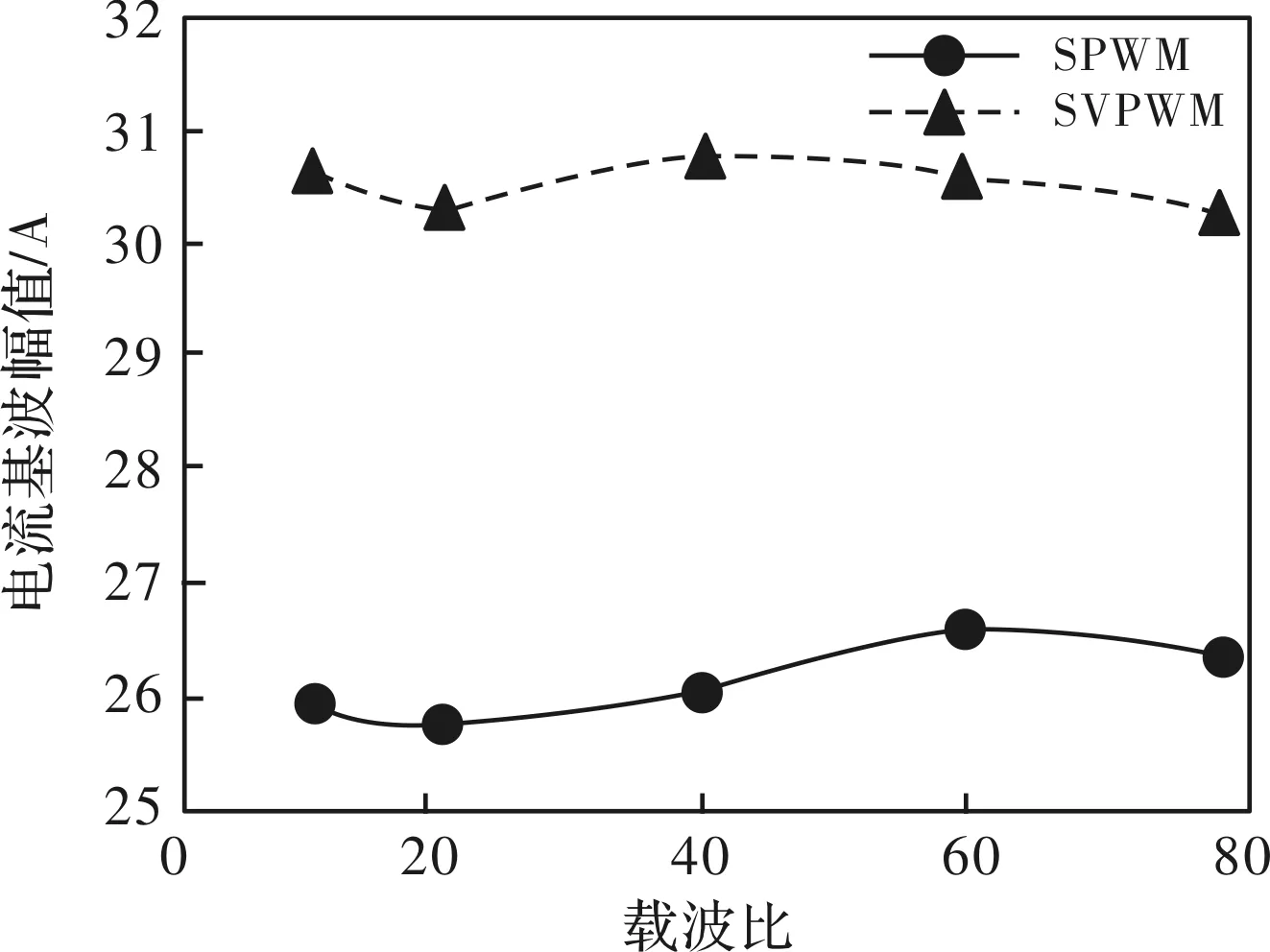
图6 M=0.6下，N与电流基波幅值关系

2.2 调制比与THD、基波电流幅值关系

从图7中能够分析得出，随着调制比的增加，谐波畸变率呈线性减小趋势。

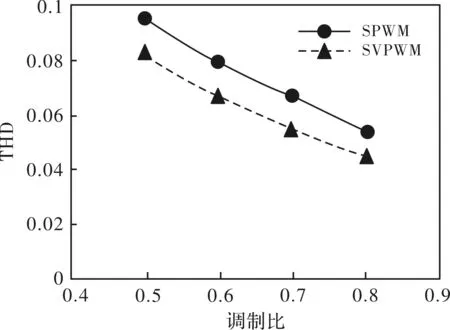
图7 N=20下，M与THD关系

从图8中得出电流基波幅值随着调制比的增加而线性增加。因此应选择较高的调制比，既能降低谐波畸变率，还能提高直流母线电压的利用率。

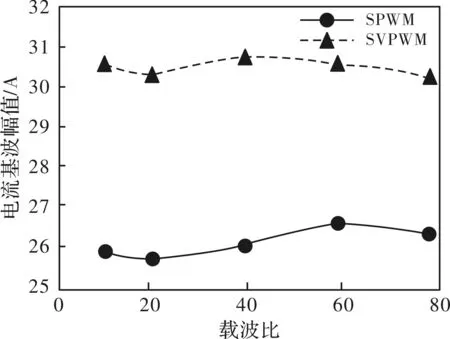
图8 N=20下，M与电流基波幅值关系

2.3 载波比对谐波分布影响

从图9分析得出，谐波电流幅值占基波2%的谐波主要集中在低次谐波区域；对于高次谐波区域，高电流幅值的谐波主要集中在载波频率以及载波频率的整数倍区域，谐波幅值占基波的1%以下。

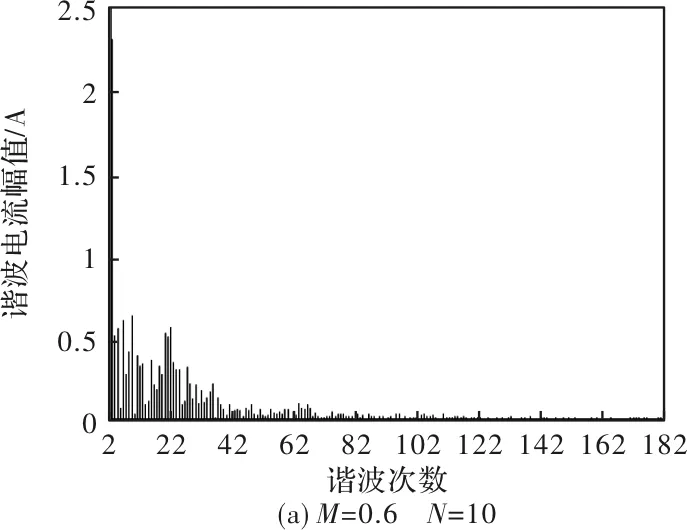
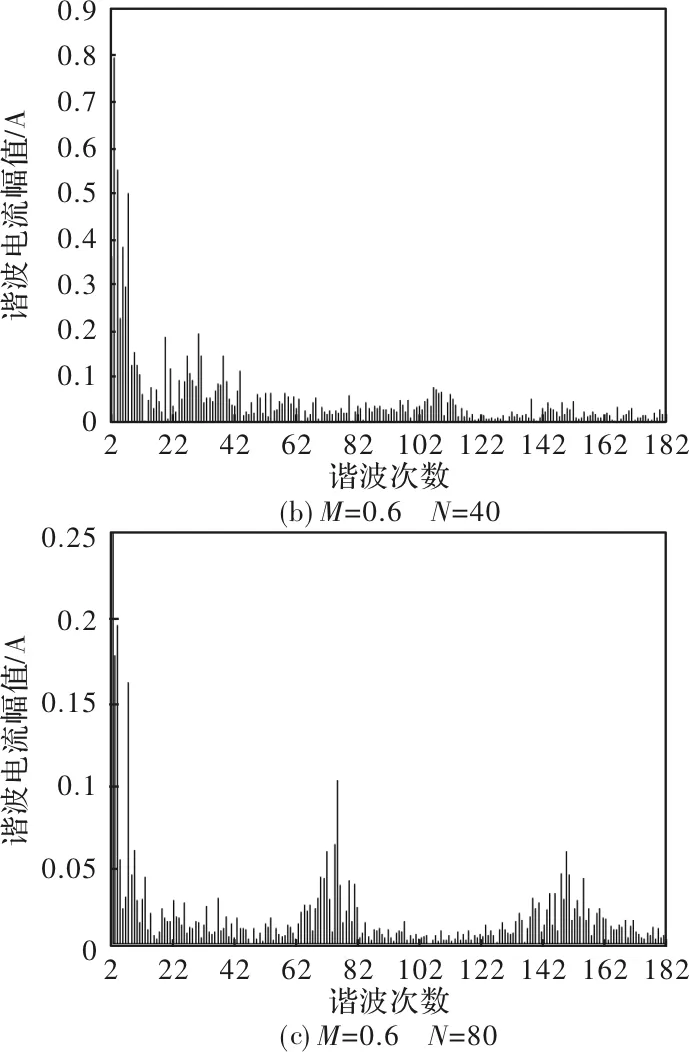
图9 SVPWM下固定调制比，改变载波比的谐波分布

2.4 调制比对谐波分布影响

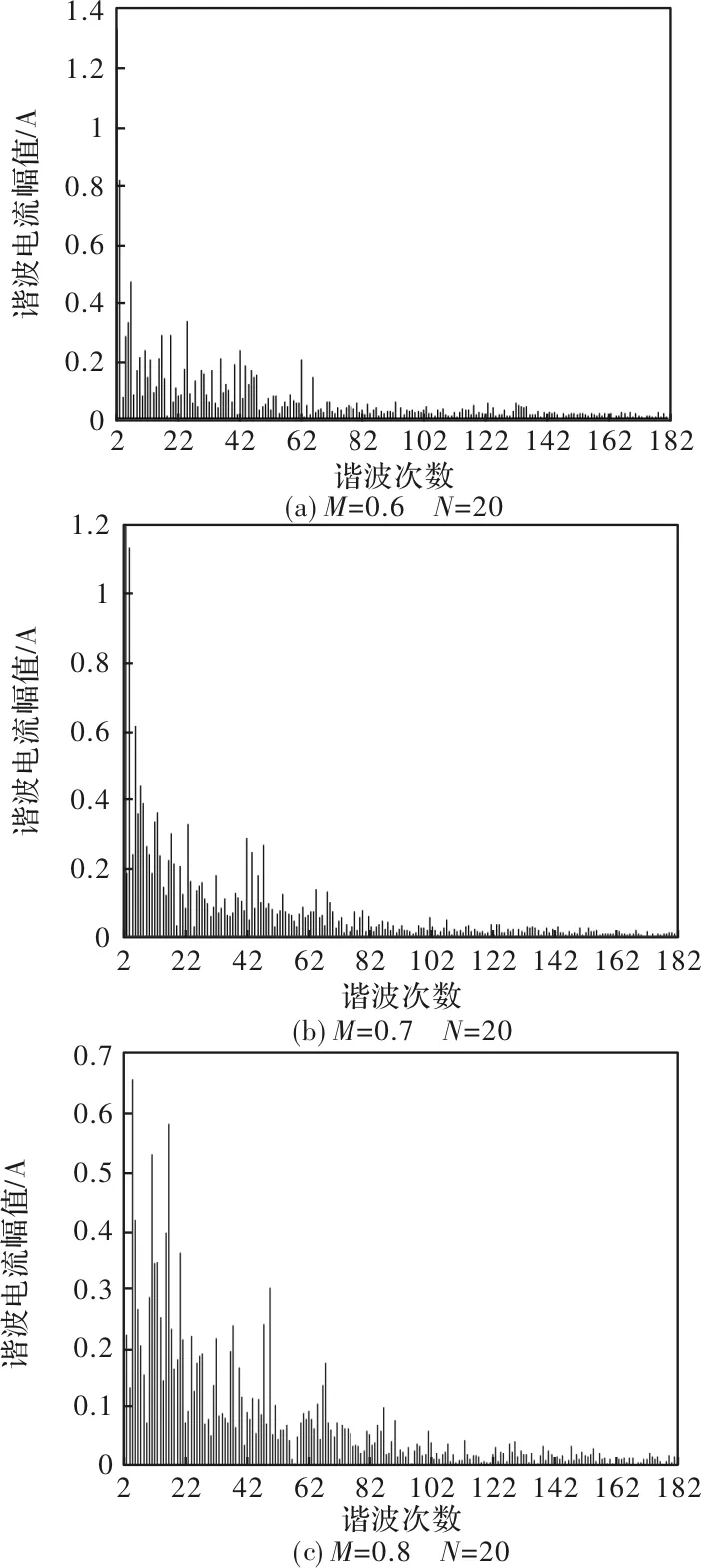
图10 SVPWM下固定载波比，改变调制比的谐波分布

3 时间谐波与电机损耗的关系

电流时间谐波产生的附加谐波损耗分别附加于定子绕组铜耗、基波铁耗、永磁体涡流损耗、周围金属结构件涡流损耗。利用Simulink、Simplorer、Maxwell场路耦合法分别计算负载变频器供电及负载正弦供电的永磁电机损耗，两者相减为附加谐波损耗。将采用SVPWM调制方式，变频器载波比为50，调制比为0.8，对永磁电机附加谐波损耗进行仿真计算。

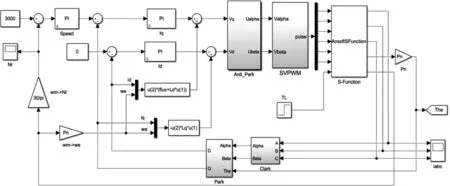
图11 三相永磁电机矢量控制仿真模型

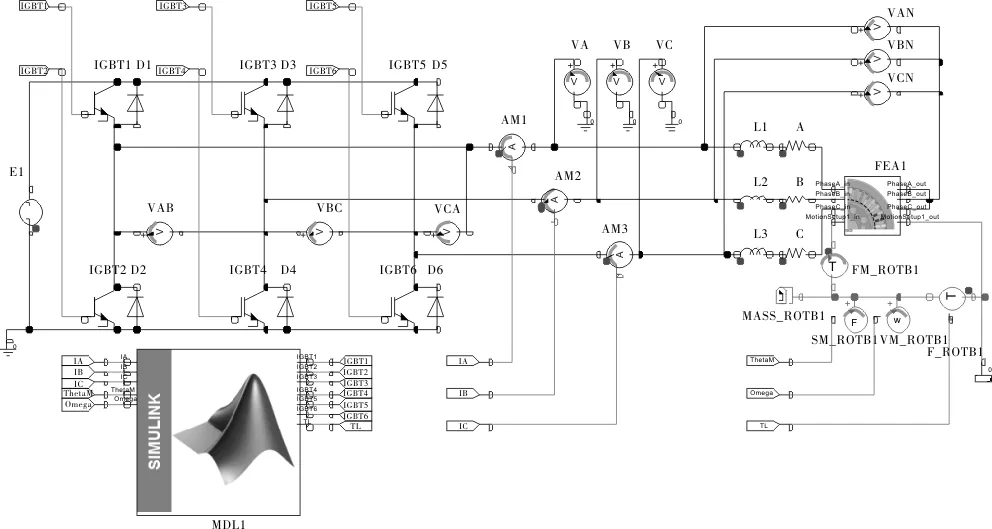
图12 三相永磁电机场路耦合联合仿真模型

3.1 电机参数

本文以表贴式永磁同步电动机为例，为了改善气隙磁密波形对永磁体进行了削角处理。永磁电机的主要参数如表1，永磁电机的截面图如图13所示。

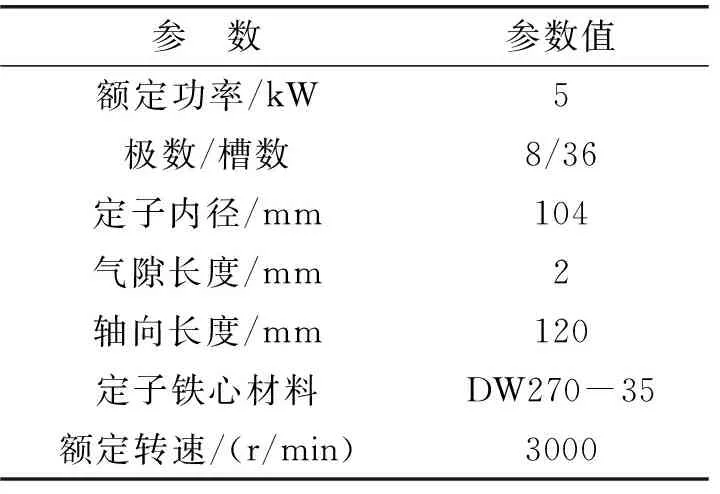
表1 表贴式永磁同步电动机主要参数

3.2 定子绕组铜耗计算

将变频器供电下的永磁电机铜耗与正弦供电下的相减，即为因时间谐波引起的铜耗增量。

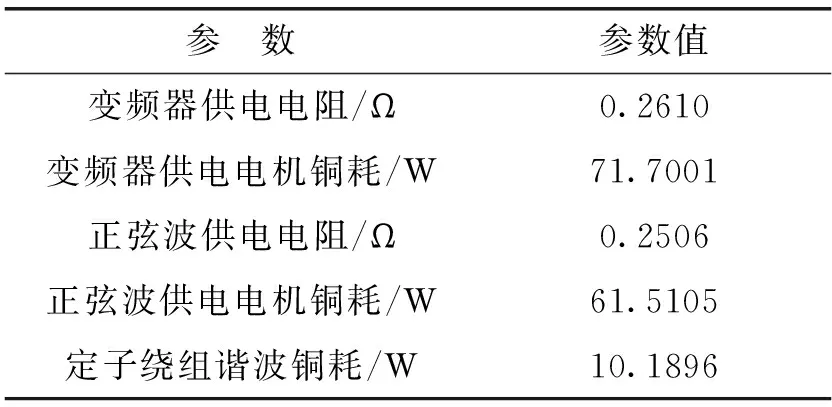
表2 永磁电机铜耗计算

3.3 定子铁心损耗计算

利用2D时步有限元法对永磁电机铁心损耗进行计算，为了更好研究时间谐波在定子铁心中的位置分布规律，现将电机定子铁心划分为四个区域：A为齿顶，B为齿身，C为齿根，D为轭部，并在永磁电机定子侧选取五个采样点如图13所示。

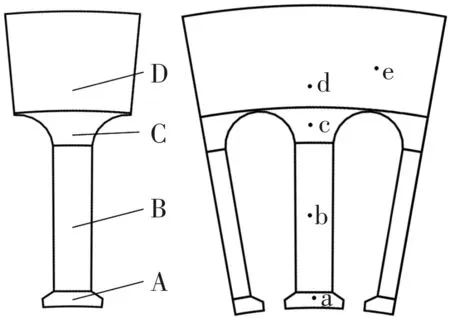
图13 电机定子区域划分及采样点选取

永磁电机磁密云图如图14所示。

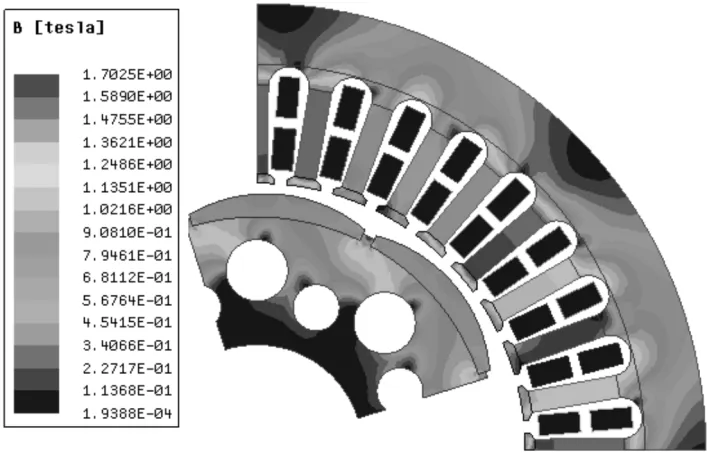
图14 电机磁密云图

由图15、图16分析得出，时间谐波对定子铁心损耗的影响主要以涡流损耗为主，定子侧的谐波损耗集中在齿身与轭部。但换成损耗密度单位时发现，附加谐波损耗密度由大到小依次为：齿顶、齿身、齿根、轭部。

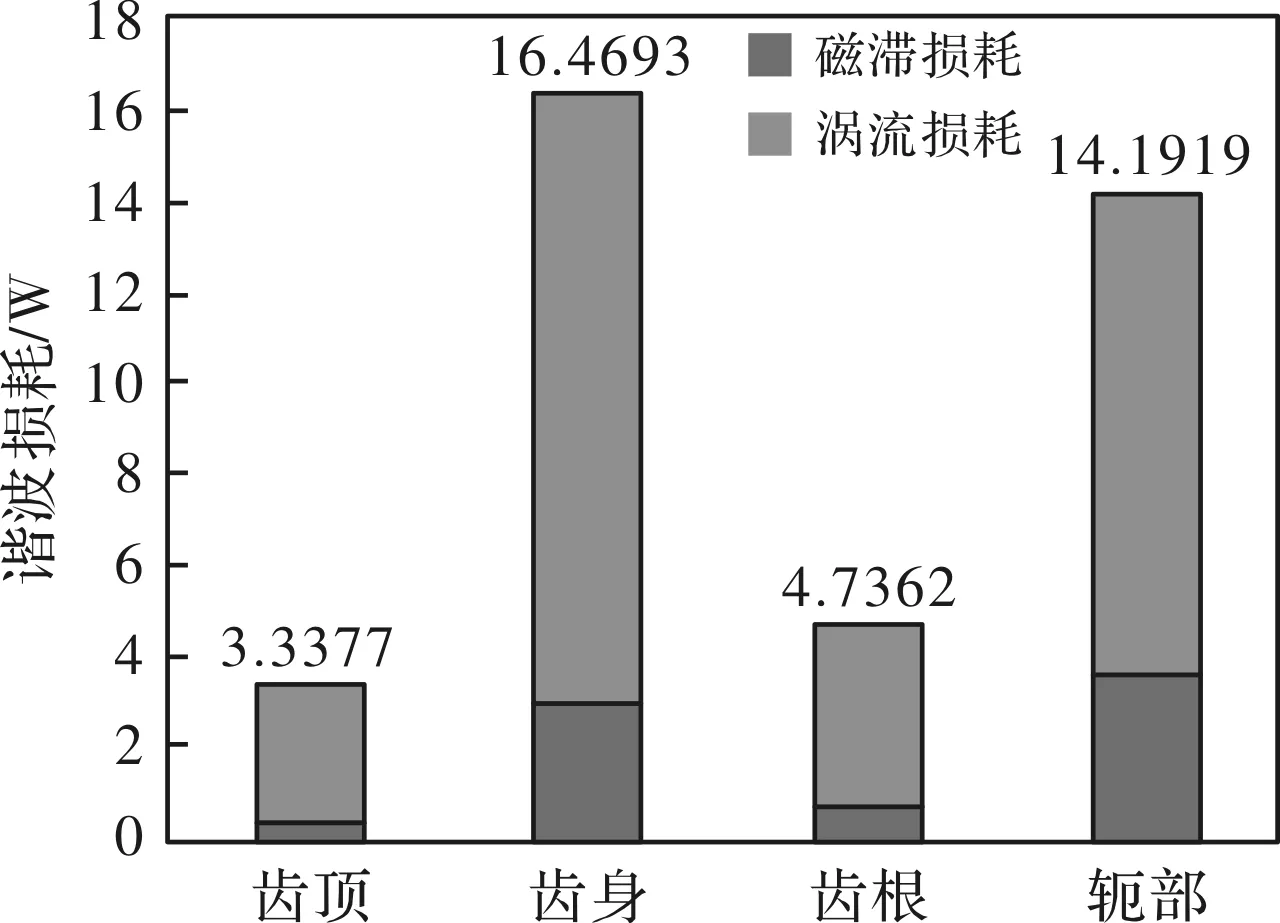
图15 电机铁心附加谐波损耗分布

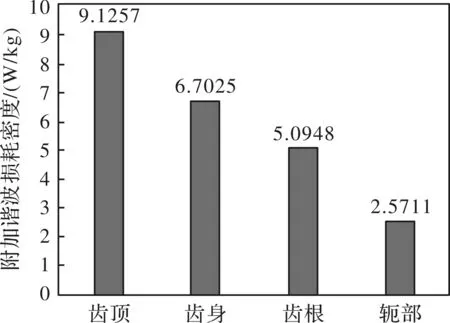
图16 定子区域附加谐波损耗分布

从图17中分析得出，变频器供电时各区域磁通密度变化范围比正弦波供电时大，并且磁密变化轨迹具有很多毛刺。从磁密磁化方式考虑，齿身仅为交变磁化，齿顶与齿根旋转磁化磁密主要为径向分量，轭部旋转磁化磁密主要为切向分量。

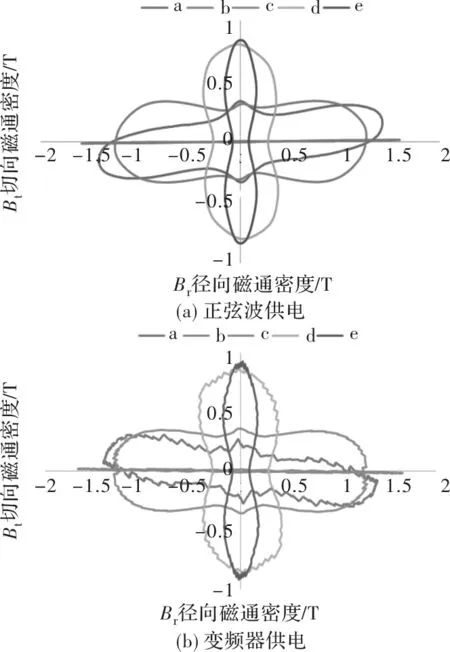
图17 空载下定子磁密变化

3.4 永磁体及周围金属构件损耗计算

针对永磁体和周围金属结构件附加谐波引起的涡流损耗增量部分，采用3D时步有限元法对其涡流损耗进行计算，如图18所示。

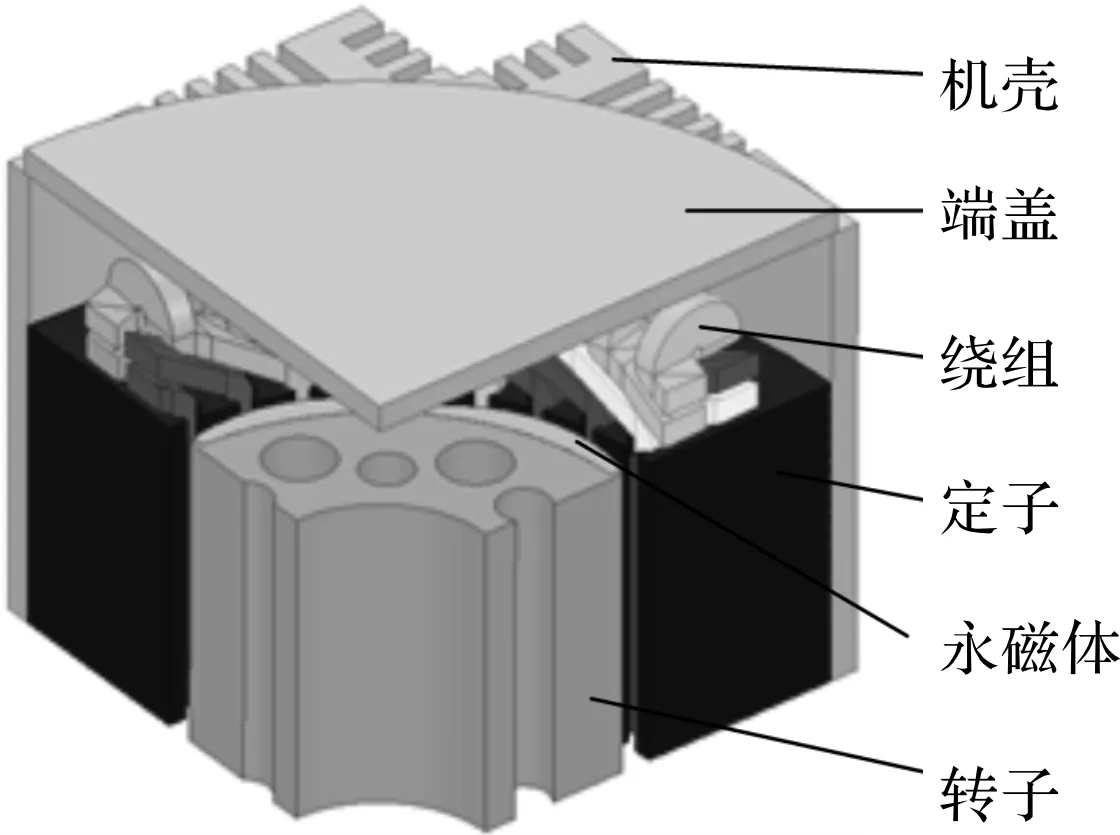
图18 电机3D有限元模型

通过表3得知，时间谐波对电机周围金属构件的影响不大，主要因时间谐波磁场的非同步转速对转子上永磁体造成涡流损耗较大影响。

表3 永磁体及周围金属构件涡流损耗计算

4 电机试验

本文将采用IEC60034-2-3:2013提出的附加谐波损耗的试验方法，结合现有的试验设备，为被试电机提供两套供电电源。由于正弦波电源需要较高的频率，不同于工频电，并且变频驱动永磁电机不能直接全压起动，需要搭建一套正弦波机组，作为正弦波电源使用，电机试验原理图如图19所示。

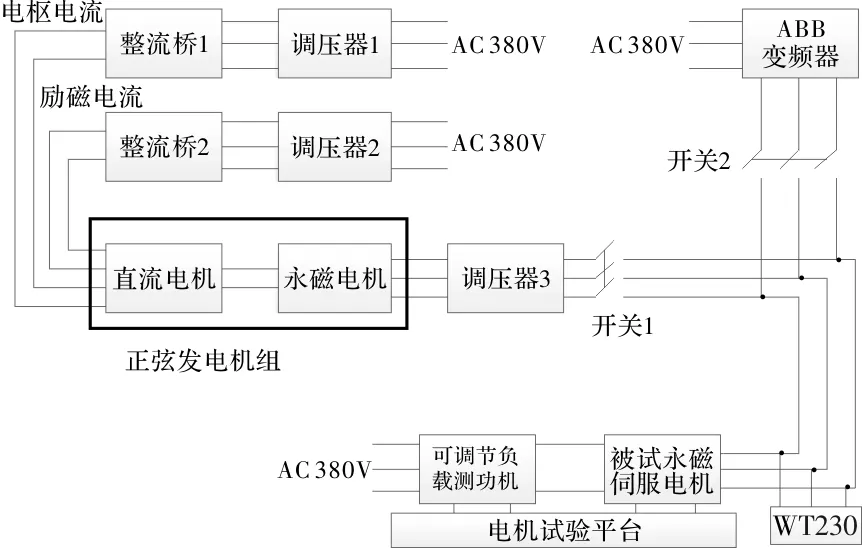
图19 试验原理图

根据国家试验标准，认为电机附加谐波损耗是随着电机负载变化而发生改变，为此将其分为恒定附加谐波损耗与负载附加谐波损耗两部分，如图20所示，永磁电机试验平台搭建如图21所示。

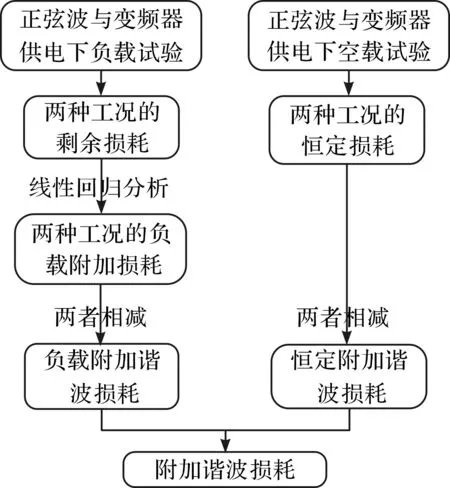
图20 附加谐波损耗试验计算流程

对于试验方法中铁心损耗部分引入如式(6)所示，对负载时的铁耗进行修正。

(6)

式中，BδN为负载气隙磁密值；Bδ0为空载气隙磁密值；PFe0为空载铁心损耗。

图21 电机试验平台

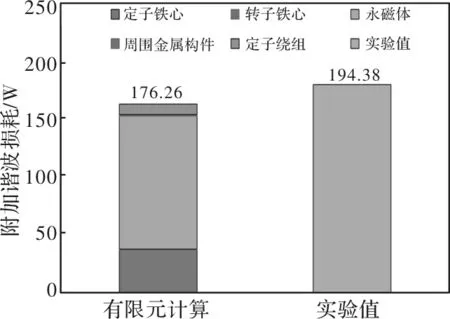
图22 5kW永磁电机计算值与试验值比较

表4 附加谐波损耗计算修正系数

通过以上数据比较分析得出，5 kW永磁电机附加谐波损耗修正系数为1.10，由于电机场路耦合仿真并未考虑到电机机械损耗，为此误差在可接受范围，有限元计算时发现时间谐波对转子铁心与电机周围金属构件的影响较小。参考国家对电机损耗的试验标准，试验电机的附加谐波损耗占总损耗的42.56%，占电机输出功率的3.89%。