锥b-度量空间中非线性压缩自映射对的一致点新结果

王忠谦

（江苏第二师范学院 数学与信息技术学院，江苏 南京 210013）

Jungck首先研究度量空间中弱相容自映射对的一致点及其应用[1-2]，2007年Huang等提出锥度量空间的概念[3]，是度量空间的重要推广。此后，许多学者先后在锥度量空间中得到相应的弱相容自映射对的一致点存在与唯一性结果[4-6]。Hussian等结合b-度量的性质，提出锥b-度量空间的概念，是b-度量空间与锥度量空间的重要推广[7]。而后，多位学者分别在锥b-度量空间中建立了一些映射的不动点与重合点定理[8-10]。但上述结果都是在一般广义压缩条件小于1的情况下讨论的，目前尚无对压缩条件大于1情形的研究。基于这一点，本研究的主要工作是在容许压缩条件不小于1的情况下，在锥b-度量空间中建立了一个弱相容非线性压缩自映射对的一致点和重合不动点的存在性与唯一性定理，并举例说明本研究的结果是对已有文献[3,4,8,10,11]中相应存在性和唯一性结果的改进和补充。

1 预备知识

设E是一个实的Banach空间。如果E中一个子集P满足下列条件，则称P为E中的一个锥:

（a）P是闭的、非空的且P ≠{θ}；

（b）对任意的a,b ∈ℝ+,x,y ∈P有ax + by ∈P；

（c）P ∩(-P) ={θ}。对于给定的E 中锥P，定义关于P 的偏序为:x ≤y ⇔y - x ∈P[3]。如果存在K ＞0，当θ ≤x ≤y 时，有‖ x ‖≤K‖ y ‖成立，则称锥P为正规的。如果int P ≠∅，锥P称为体锥。

下文中，总是假设E是一个实的Banach空间，P是E中的一个体锥，≤是关于P的偏序。

定义1［7］设X ≠∅，s ∈[1,+ ∞)给定，如果映射d:X × X →E 满足下列条件，则称d 是X 上的一个锥b-度量，(X,d)是一个锥b-度量空间:

（d1）对任意的x,y ∈X，有d(x,y) ≥θ，并且d(x,y) = θ当且仅当x = y；

（d2）对任意的x,y ∈X，有d(x,y) = d(y,x)；

（d3）对任意的x,y,z ∈X，有d(x,y) ≤s[d(x,z) + d(z,y)]。

如果s= 1，则称d是X上的一个锥度量，(X,d)是一个锥度量空间［3］。

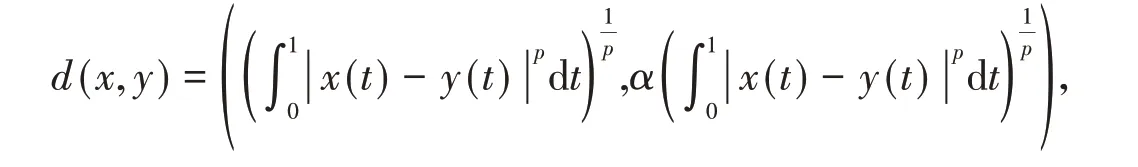
定义2[7]设(X,d)是一个锥b-度量空间，x ∈X，{xn}⊂X。

（1）如果对任意的c ∈E，θ ≪c，存在N ∈ℕ，使得d(xn,x) ≪c(∀n ＞N)，则称{xn}收敛于x，记为xn= x或者xn→x。

（2）如果对任意的c ∈E，θ ≪c，存在N ∈ℕ，使得d(xn,xm)≪c(∀n,m ＞N)，则称{xn}是一个Cauchy列。

（3）如果每一个X中的Cauchy列都收敛于X，则称(X,d)是完备的锥b-度量空间。

引理1[7]设(X,d)是一个锥b-度量空间，x ∈X，{xn}⊂X，则

（2）{xn}是一个Cauchy列的充要条件是d(xn,xn+m)→θ(n,m →∞)。

定义4[11]设f、g是X中两个自映射，如果对一些x ∈X，有w= fx = gx，则称x是f、g的一致点，并称w是f、g在一致处的点。

定义5[4]如果锥b-度量空间(X,d)中的两个自映射f、g在它的一致点处是可交换的，则称f、g为弱相容的，这意味着如果fx = gx，则gfx = fgx。

2 主要结果

定理1 设(X,d)是锥b-度量空间且系数s ∈[1,+ ∞)，如果映射f、g:X →X 满足f(X) ⊂g(X)，且f(X)或者g(X)是X的完备子空间，对任意的x,y ∈X，有

这里φi:X × X →[0,+ ∞)，i =1，2，3，4，5。如果φi满足条件

（i）对任意的x,y ∈X，有φ1(x,y) + φ4(x,y) + φ5(x,y) ＜1；

（iii）a ＞0，b ＞0且A ≥0，B ≥0；

则f、g在X中有一致点，且一致处的点唯一。如果f、g是弱相容的，则f、g有唯一的重合不动点。

证明 任取x0∈X，据条件可知，存在x1∈X，使得fx0= gx1。由归纳的方法构造X中序列{xn}使得fxn=gxn+1。

对于n =0,1,2，…，根据式（1）及定义1，能够得到

和

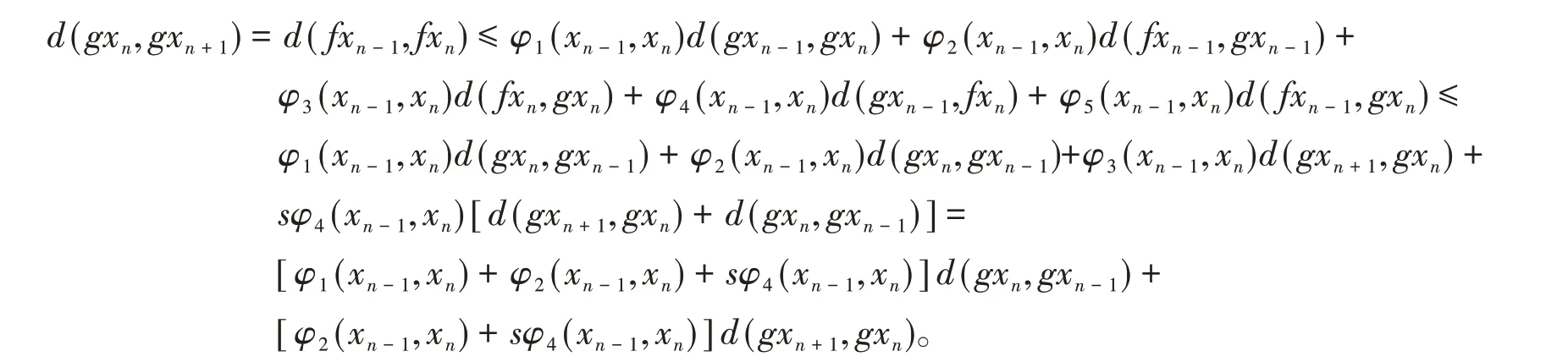
由条件（ii），能够得出

和

由以上可得

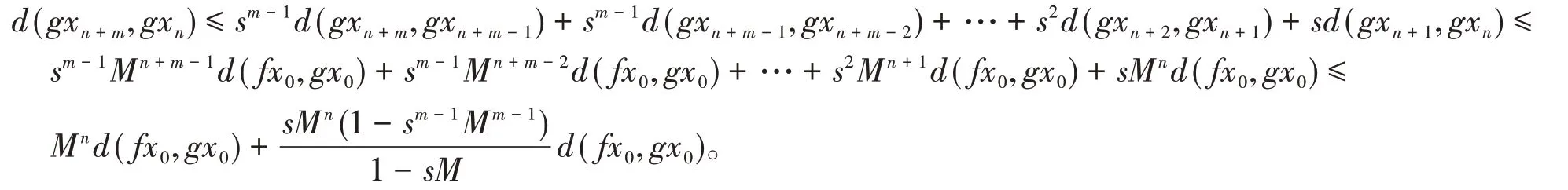
由此可得

表明对任意的n ＞N1，m ∈ℕ*有d(gxn+m,gxn)≪c，即{gxn}是X中的一个Cauchy列。

根据条件，f(X)或者g(X)是X 的完备子空间，可得fxn-1= gxn→y*∈f(X)或者g(X)，并且存在x*∈X使得gx*= y*。n =0，1，2，…，根据式（1）及条件（ii），有

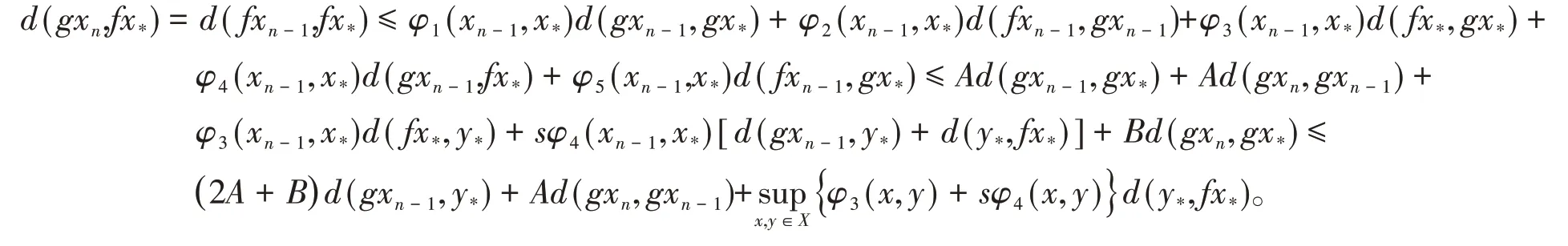
{gxn}是X中的一个Cauchy列，根据引理1及上式，有

下面说明f、g在X中一致处的点的唯一性。利用反证法，假设还存在另一点x*∈X使得gx*= fx*。于是，由式（1），可得

由条件（i），可得d(gx*,gx*)= θ，即gx*= gx*。

进一步，如果f、g是弱相容的且u = fx = gx，则fu = fgx = gfx = gu，说明fu = gu也是f、g在X中一致处的点。再据上述证明的一致处的点的唯一性可得u = fu = gu，即u 是f、g 的重合不动点。另外，如果-u= f -u=g-u，则-u是f、g在X中一致处的点，由唯一性可知u = -u。证毕。

任何一个非线性压缩都包括一个线性压缩作为其特例。据定理1不难得到下述推论。

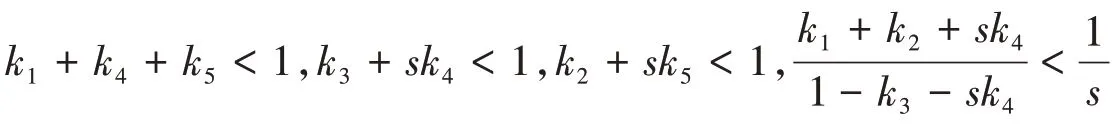
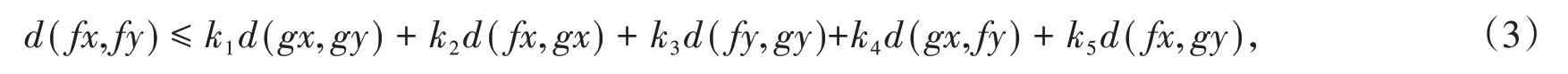
定理1的结论仍然成立。

注2 设推论1中映射g是恒等映射，可证明映射f的不动点的存在唯一性定理。锥b-度量空间在s= 1的情况下，推论1中压缩系数变为

3 例子与结论

例1 设X ={1,2,3}，E = ℝ2，P ={(x,y):x ≥0,y ≥0}。映 射d:X × X →P 定 义 为d(1,1) = d(2,2) =d(3,3) =(0,0)，d(1,2) = d(2,1) = d(1,3) = d(3,1) =(1,1)，d(3,2)= d(2,3) =(2,2)，则(X,d)是完备的锥b-度量空间且系数s= 1。再定义两个映射f、g：X →X为

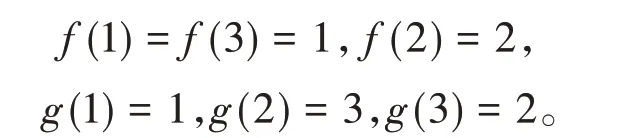
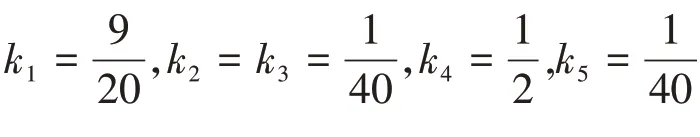
进一步，当x = 2、y = 3时，有

当x = 3、y = 2时，有

当x = 1、y = 2时，有

当x = 2、y = 1时，有

根据d(f(1),f(1)) = d(f(2),f(2))= d(f(3),f(3)) = d(f(1),f(3) = d(f(3),f(1)))=(0,0)，易得推论1 的条件都满足，所以f、g有唯一的一致处的点，且x = 1是一致点。由于f、g是弱相容的，说明x = 1是f、g的唯一重合不动点。但对于任何ki≥0(i = 1,2,3,4,5)且k1+ k2+ k3+ k4+ k5＜1，有当k3≤k2时，

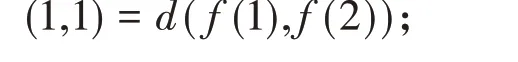
当k3＞k2时，

说明f、g不满足文献[3-4,10]中一般广义压缩条件k1+ k2+ k3+ k4+ k5＜1。

4 结束语

本研究证明了当压缩条件k1+ k2+ k3+ k4+ k5＞1 时，在锥b-度量空间下，非线性压缩自映射对的一致点和重合不动点的存在性与唯一性定理，并举例说明本研究的结果改进和补充了已有文献中相关的存在性和唯一性定理。