BP神经网络补偿ADRC在PMSM控制中的研究

李寅生，陈永军

(长江大学 电子信息学院，湖北 荆州 434023)

0 引 言

传统的PMSM矢量控制系统采用内环电流环外环速度环的双闭环控制策略，双环内的电流控制器和速度控制器均采用PI控制算法。然而传统PI控制存在着对参数变化敏感、抗干扰能力差和积分环节容易导致系统震荡不稳定等不利因素[1]。

鉴于传统PI控制存在的一系列问题，自抗扰控制(ADRC)作为一种改进于传统PI的非线性控制算法，利用扩张状态观测器(ESO)对系统未建模动态、参数变化和系统外扰所引起的综合扰动进行观测并进行补偿，可有效提高控制系统的鲁棒性和抗干扰能力，ADRC取消了反馈控制中的积分环节，通过补偿干扰量消除稳态误差，优化了控制的稳定性。出于ADRC的优异动稳态性能，其被广泛应用于PMSM矢量控制，文献[2]采用二阶ADRC整合PMSM矢量控制的位置环和速度环，并采用一阶ADRC作为电流控制器，有效改善系统的动稳态性能；文献[3]利用ADRC实现电机的解耦控制，并利用ESO直接电机位置角和转速，实现永磁同步电机无位置传感器控制；文献[4]采用简化的自抗扰控制器对永磁同步电机进行控制，取消了TD模块，简化了参数整定，优化了系统的实时性。然而以上三种方法均未考虑ADRC存在的局限性：ADRC的性能受到了干扰类型的制约，应对大幅度高速率变化的干扰，ADRC控制器显得捉襟见肘。

由于传统自抗扰控制器的扩张状态观测器(ESO)对干扰的观测精度受干扰量变化的影响[5]，传统ESO要跟踪上变化速率和幅度较大的干扰必须设置较大的观测增益系数，然而过大的观测增益系数会引起系统的稳态抖震，造成不稳定，这样就存在稳定性与抗干扰的一个矛盾。为解决这个问题，文献[5]提出利用模型补偿降低ESO观测的干扰量，降低ESO的观测负担。文献[6]对电机的转动惯量和负载转矩进行辨识并补偿给ESO,减少了ESO的干扰观测量，但是该方法算法复杂，运算量较大，不利于控制的实时性。

本文提出了新的方法，速度环采用简化的一阶ADRC作为速度控制器，同时利用BP神经网络出色的非线性函数拟合能力[7]对永磁同步电机的干扰函数进行离线识别，然后再将训练好的神经网络运用于对ESO干扰量的补偿，降低ESO的观测负担，进而提高观测精度，优化控制器的抗干扰能力。另外为了对负载转矩进行实时辨识，设计了降阶伦伯格负载转矩状态观测器[8],实时对电机所受负载转矩进行观测，并将观测的负载转矩数据用于BP神经网络的离线训练输入和在线输入。

1 PMSM数学的模型

研究的是表贴式永磁同步电机，忽略PMSM的涡流和磁滞损耗，假设其磁路不饱和，可以建立在d-q坐标系下的PMSM的微分方程组：

(1)

式中，R和Ls分别表示电机的定子电阻和电感；φf是永磁体磁链；id、iq是定子电流的d-q轴分量；J和B分别是电机的转动惯量和阻尼系数；w，TL分别是机械角速度和负载转矩；pn是极对数。

采用id=0的电流控制策略，则式(1)转化为如下：

(2)

由式(2)可知，电机所受的主要未知干扰为TL，其直接作用于电机的转速微分方程。

2 自抗扰控制PMSM

2.1 自抗扰控制

传统自抗扰控制器由三部分组成，微分跟踪器(TD)、扩张状态观测器(ESO)和状态反馈控制律。微分跟踪器(TD)合理安排给定输入的过渡并求取其各阶微分，避免阶跃输入引起的启动超调；扩张状态观测器(ESO)以系统内外综合扰动作为扩展状态量，对其进行估测；非线性状态误差反馈控制律(NLSEF)对TD与ESO的各阶误差进行非线性组合得到非线性反馈控制量，然后利用ESO估测的综合干扰量对反馈控制量进行补偿，得出最终控制量。

由于传统ADRC采用的非线性函数参数整定复杂，不利于工程实际应用，本文对ADRC进行简化：采用直接误差取代原非线性函数，将ESO和NLSEF线性化，保留非线性TD。

以一阶ADRC为例，假设某一阶被控对象的状态空间模型为：

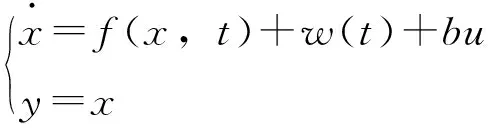
(3)

其中，将f(x,t)+w(t)视为被控对象的内外综合扰动，u为控制量，x是系统状态量，b为控制增益，设计以下一阶简化ADRC：

(1)一阶非线性TD

(4)

(2)二阶线性化ESO

(5)

(3)线性化反馈控制律

(6)

其中，z11为给定输入，z21为x的跟踪值，z22为综合干扰的估测值，[β01,β02]为ESO状态反馈增益矩阵，其中β02决定了z22对真实扰动变化的响应速度，r是TD跟踪快慢因子，b0是估测的控制增益。fal(·)是非线性函数，表达式如下：

(7)

式中，α为非线性因子，δ线性区间宽度。

2.2 简化的一阶自抗扰速度控制器

由(2)可知，转速微分方程为一阶微分方程。在矢量控制系统中，大部分干扰发生于速度环以内，电流环以外。所以可以采用一阶ADRC控制器作为速度控制器以提高速度环的抗干扰能力，而电流环则沿用传统PI控制器作为电流控制器。

由式(2)可得PMSM矢量控制速度环被控对象状态方程如下：

(8)

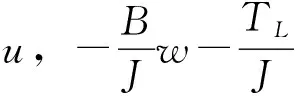
(9)

式中，

(10)

根据(4)、(5)和(6)可得简化的一阶自抗扰速度控制器形式如下：

一阶TD:

(11)

线性化的二阶ESO:

(12)

比例误差反馈控制律：

(13)

简化的一阶ADRC速度控制原理如图1所示。

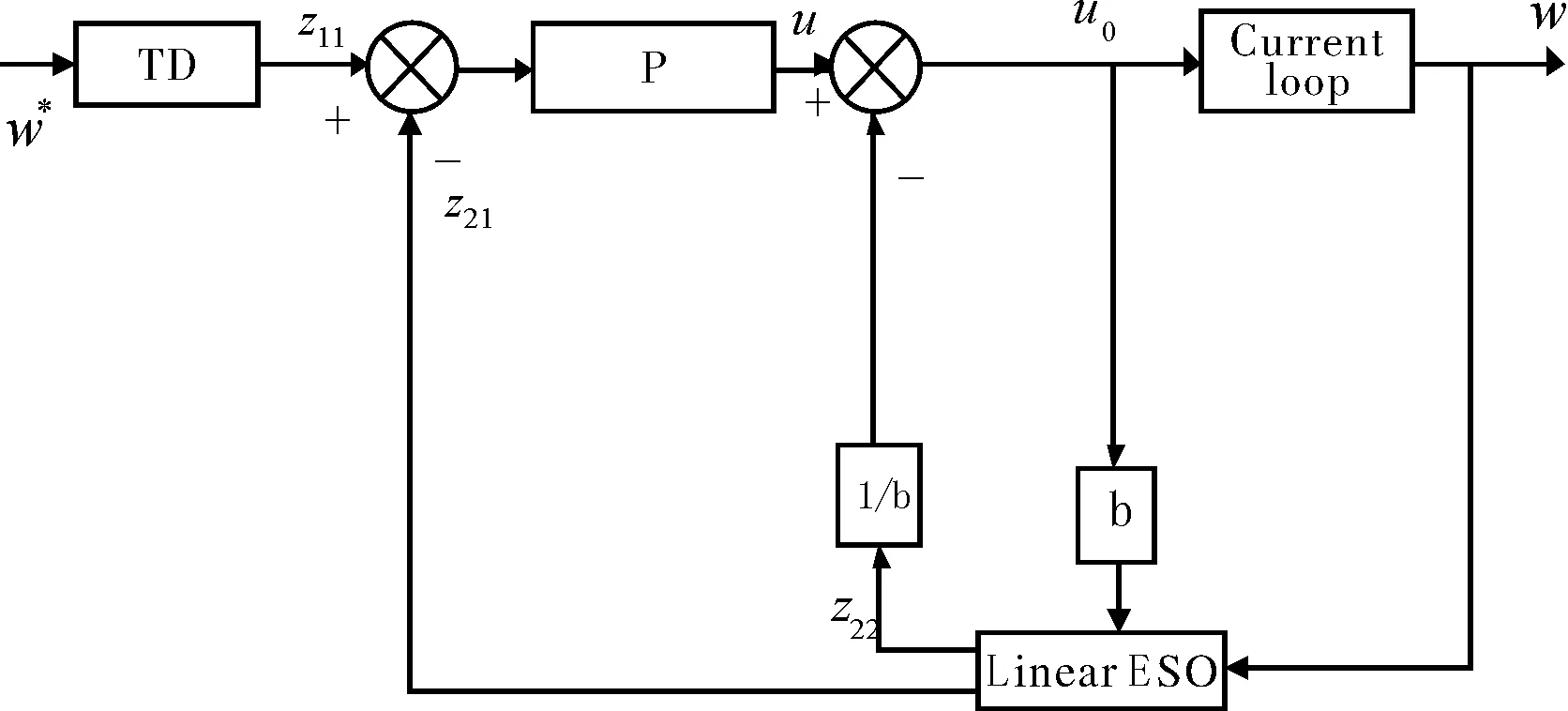
图1 一阶简化ADRC速度控制原理图

3 神经网络补偿ADRC

3.1 PMSM的ADRC补偿优化

由PMSM矢量控制速度环控制对象的状态方程(9)和一阶简化ADRC形式可知，在干扰量f(w,TL)完全不可知的情况下，ESO要观测的综合干扰量为

z22=f(w,TL)+(b-b0)u

(14)

当发生的干扰量变化过大，这时为了保证观测器的收敛速度，必须设置较大的观测增益系数β02，然而过大的β02会引起稳态观测值的抖震，造成就系统不稳定，过小的β02会削弱ESO对干扰的响应速度，弱化了ADRC的抗干扰能力,系统的鲁棒性下降。因此这就需要在系统稳定性和抗干扰能力之间做一个折中，这无疑大大限制了ADRC的性能。

为了保证ADRC稳定性的同时最大限度地提高系统的抗干扰能力，就要减少z22所要观测的干扰量幅度。由(14)可知，可将f(w,TL)分为两部分

(15)

f0为系统的可辨识干扰，f1为系统的未知干扰，如果将f0补偿给ESO,则z22只需要观测剩下的f1+(b-b0)u。这样就能降低ESO的估测负担，使其在较小的β02下也能快速跟踪上余下的干扰量，提高了ESO对干扰量的观测精度，优化ADRC的抗干扰能力。

3.2 BP神经网络辨识补偿ADRC

由以上分析可知，实现ADRC补偿优化的关键是辨识出系统的f0。只要辨识的f0越接近f(w,TL),最终ESO所要观测的z22就会越小，观测精度就会越高。由于f(w,TL)里边的J和B是未知的，要对f(w,TL)进行辨识，就必须先辨识出J和B是未知的，这无疑会带来较大的运算量，不利于控制的实时性。

为了更加快捷地实时辨识出f(w,TL)，本文提出了一种新的方法：利用BP神经网络出色的非线性函数拟合能力对f(w,TL)进行辨识并将辨识好的f(w,TL)补偿给ESO。

BP神经网络具有出色的自学习能力，通过对样本的训练和学习修正网络内部的权值，能有效拟合各种未知函数。假设f(w,TL)就是这样一个未知函数，利用BP神经网络辨识表达f(w,TL)。

具体实现方法：

(1)确定BP神经网络的拓扑结构，由式子(15)可知，应设定神经网络输入为w、TL,目标输出为z22。因此输入层节点数是2，输出层节点数是1，经过多次仿真修正隐含层节点数，当隐含层节点数为5时，神经网络拟合效果最好。

(2)设置好一组控制器参数，使ADRC平滑稳定控制好永磁同步电机，采集系统稳态数据作为训练样本。

(3)利用已收集的训练样本对神经网络进行离线训练，离线拟合系统干扰函数。

(4)把训练好的神经网络fNN嵌入到永磁同步电机一阶ADRC速度控制器中，用以补偿ESO。

基于BP神经网络补偿ADRC的形式如下：

(1)BP神经网络补偿的二阶线性ESO:

(16)

(2)BP神经网络补偿的比例误差反馈控制律：

(17)

基于BP神经网络补偿优化的ADRC转速控制原理图如图2所示。

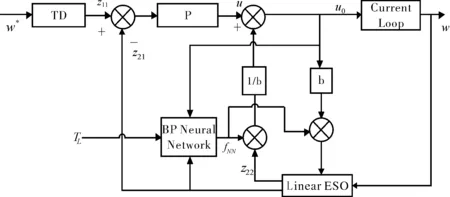
图2 神经网络补偿ADRC速度控制原理图

4 负载转矩状态观测器

神经网络的输入参数包含负载转矩，由于负载转矩是一种难以利用传感器测量的物理量，本文采用了降阶的伦伯格状态观测器对负载转矩进行实时检测。

假设负载转矩在单个控制周期内保持不变。

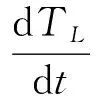
(18)

以TL作为系统的扩展状态量由方程(8)可得系统的状态空间模型：

(19)

根据(19)可得降阶的伦伯格负载转矩观测器形式如下：

(20)

K=[k1k2]T是状态反馈增益阵。

设状态观测器的期望极点为α，则可得状态误差特征方程

|SI-(A-KC)|=(S-α)2

(21)

忽略阻尼系数,可得

(22)

当α处于负平面时，观测误差渐进收敛于0。

将伦伯格状态观测器实时估测的负载转矩与z21一道直接输入到离线训练好的神经网络中，得出干扰补偿量fNN。

5 PMSM矢量控制仿真与分析

在Matlab/Simulink上利用S函数设计出一阶简化ADRC和负载转矩观测器。仿真所用PMSM模型参数如表1所示。

仿真验证主要分为以下两部分：

(1)验证ESO增益系数β02对系统稳态稳定性及抗干扰能力的影响。

(2)验证神经网络补偿ADRC的优化效果。

仿真设定的ADRC参数为：r=1000，α0=0.5，δ0=0.01，β1=3，b0=256.73，β01=4800，β02为仿真变量。

为了验证β02对系统稳态稳定性和抗干扰能力的影响，将其设置成不同的数值，对不同β02下的干扰补偿量z2和抗负载能力进行分析。

速度环采用一阶简化ADRC，根据图1搭建仿真模型，空载工况下，设置转速在0 s由0阶跃到，在0.25 s时突加大小为20 Nm的阶跃负载。当增益系数β02分别取值1760 000、3760 000、5760 000时，ESO观测所得综合干扰z2分别如图3的a、b和c所示。

当增益系数β02分别取值1760 000、3760 000、5760 000时，突加负载部分的转速响应曲线如图4的a、b和c所示。

由图3突加负载部分可知，随着β02的增大，ESO对阶跃负载的响应速度越快，抗干扰能力越强。

由图4可知，随着β02的增大，电机在突加负载下的转速降越小，转速恢复时间越短，这也直接印证了，β02越大,ADRC速度控制器的抗干扰抗负载能力越强。

以上仿真得出一个结论：β02越大，系统稳态稳定性越差，抗干扰能力越强。综合对系统稳定性和抗干扰能力的要求，β02的取值必须做一个折中。

为了最大限度地实现ADRC速度控制器稳定性和抗干扰能力双优化，采用BP神经网络补偿ADRC方案，利用Matlab的神经网络工具包搭建离线BP神经网络，并通过仿真收集的稳态数据对神经网络进行离线训练。最后把训练好的BP神经网络嵌入ADRC中，根据图3搭建出基于BP神经网络补偿ADRC永磁同步电机矢量控制系统。为了保证模型具有良好的稳态稳定性，取β02=1760 000。

图5 转速响应曲线局部放大

图6 ESO的干扰观测值

图波形

由图5可知，突加20 Nm负载后，采用BP神经补偿ADRC速度控制器的电机出现的最大转速降为41.5 r/min，再次恢复到稳态所用时间约为0.0055 s；采用不带补偿的ADRC速度控制器的电机则出现47 r/min的最大转速降，恢复到稳态的时间用了0.0131 s。显然，采用BP神经补偿ADRC有效提高PMSM矢量控制系统的抗负载抗干扰能力。

由图6可知，采用BP神经网络补偿后ADRC的ESO在启动阶段和突加负载阶段的观测干扰值波动幅度较无补偿的要小。尤其在突加负载阶段，由于添加了BP神经网络对干扰量的补偿，ESO观测干扰的波动幅度远小于无补偿ADRC,这无疑大大降低了ESO的观测负担，提高了ESO对干扰量观测精度，降低了对ESO响应速度的要求，使其在较小的反馈增益系数β02下也能保持较优的抗干扰抗负载能力，这也是BP神经网络补偿ADRC实现稳态稳定性和抗干扰能力双优化的机理。

6 结 论

采用一阶简化ADRC作为永磁同步电机矢量控制系统的速度调节器，可有效提高系统的动稳态特性，优化系统的抗干扰能力与鲁棒性。

针对ESO存在抗干扰能力和稳态稳定性必须折中处理的问题，提出了BP神经网络补偿ADRC的方法。利用BP神经网络去识别干扰函数，并将其补偿给ESO,有效减少ESO观测的干扰量幅值，使其在较小的反馈增益系数β02下也能维持较好的抗干扰能力，实现了ADRC稳态稳定性和抗干扰能力的双优化。