计及移相角的多边形自耦变压器12脉波整流系统分析

王佳荣，张正焓，陈小强，3

(1． 兰州交通大学 自动化与电气工程学院， 甘肃 兰州 730070；2． 西南交通大学 电气工程学院， 四川 成都 610031;3． 兰州交通大学 光电技术与智能控制教育部重点实验室， 甘肃 兰州 730070)

多脉波整流由于其成本低且理论上能完全消除低次特征谐波，已广泛应用于电力系统中[1-3]。多脉波整流一般分为12、18、24、36脉波整流[4-7]。12脉波结构简单且能满足大多数用电设备对谐波的要求，在电力系统中使用较广[8-10]。移相变压器通过产生不同相位电流可抵消特征谐波[11-12]，是12脉波整流系统的核心器件。

多脉波整流系统移相原理是通过将多个不同相位的电流波形叠加以消除低次谐波，从而降低输入电流谐波[13]。在不要求电气隔离的场合，自耦变压器(Autotransformer, AT)不仅能保证多脉波整流系统良好的整流特性而且节约整流器体积，故基于自耦变压器的多脉波整流系统已成为近年研究热点[14-18]。

六边形自耦变压器因结构对称性较好，研究者对其谐波抑制方面进行了深入研究[19]。为优化六边形自耦变压器结构，使其具有升压功能，本文逐次分析移相角对12脉波整流系统输入侧电流总谐波率(Total Harmonic Distortion,THD)，输出侧电压纹波系数，多边形自耦变压器 (Kilovolt-ampere, KVA)、平衡电抗器(Interphase Reactor, IPR)、零序电流抑制器(Zero Sequence Blocking Transformer, ZSBT)等效容量的影响。提出移相90°的多边形升压变压器设计，其输出电压约为输入电压的1.414 2倍，变压器等效容量约为62.8%，较传统隔离式变压器等效容量小约37.2%。

1 基于多边形AT的12脉波整流系统

12脉波多边形AT桥式整流见图1。

图1中，n为接地点；ua、ub、uc、ia、ib、ic分别为电源电压及对应电流；ia1、ib1、ic1、ia2、ib2、ic2为移相变压器的输出电流；a、b、c为移相变压器电流输入端；a1、a2、b1、b2、c1、c2为移相变压器电流输出端；ud1、ud2为整流桥输出侧电压；id1、id2为平衡电抗器上电流；Id为负载电流方均根值。

ZSBT可对三倍频电流产生高阻抗，确保两整流桥每个二极管导通120°；IPR可吸收两整流桥输出电压的瞬时差，使两整流桥能够独立并联工作。

为消除低次谐波，AT移相角和整流桥个数之间的关系式为

( 1 )

式中:φ为自耦变压器移相角;N为整流桥个数。由式( 1 )得图1中φ为π/6。

假设输入三相电压为

( 2 )

式中：Um为多边形AT输入相电压的幅值；ω为角频率；t为时间。

在大电感负载条件下，多边形AT输出电流可表示为

( 3 )

( 4 )

式中：α=φ/2；k= 1,3,5,…。

2 移相角对整流系统运行参数的影响

本文整流系统运行参数包括输入侧线电流THD及负载电压纹波系数。

2.1 移相角对输入侧线电流THD的影响

12脉波多边形AT绕组连接图见图2。

图2中，ia1、ib1、ic1、ia2、ib2、ic2、ia1_1、ib1_1、ic1_1、ia2_1、ib2_1、ic2_1、i1、i2、i3分别为对应线圈上电流；Np、Nq分别为原边和副边上线圈的匝数。

由图2可得磁动势平衡方程为

( 5 )

基尔霍夫电流方程为

( 6 )

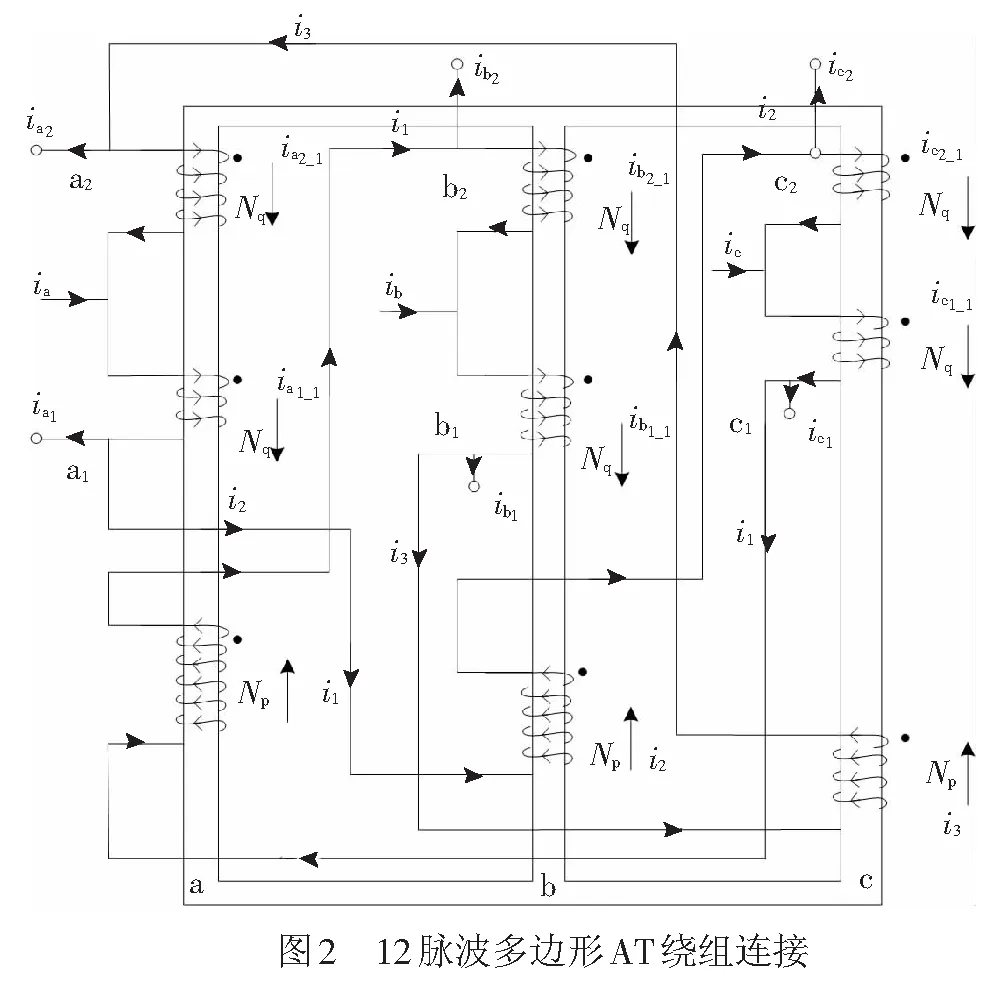
图2对应的多边形AT相量见图3。

由图3可得AT两组输出三相电压为

( 7 )

式中：Um1为AT输出相电压幅值。

并有

cosα=Um/Um1

( 8 )

为避免线圈匝数为零，则α范围应是0<α<π/3。因此φ的范围为：0<φ<2π/3。由图3可得原边和副边线圈匝比

( 9 )

因三相交流电与自耦变压器结构均对称，故φ与每相电流THD间的关系一致。可选a相电流ia为例，研究φ对输入侧电流THD的影响。则b、c相电流与a相电流具有一致变化趋势。由式( 5 )、式( 6 )，可得

(10)

电流THD定义为

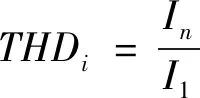
(11)

式中：THDi为电流谐波率；In为第n次谐波电流有效值；I1为基波电流有效值。

利用Matlab编程将式( 3 )、式( 4 )、式( 9 )代入式(10)中，求得ia中对应的In、I1值。将In、I1值代入式(11)可得φ与输入侧电流THD之间的关系曲线，见图4。

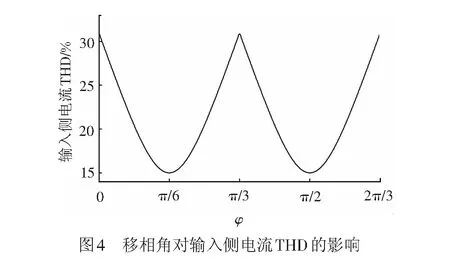
图4中，当0<φ≤π/6或π/3<φ≤π/2时，输入侧电流THD随φ的增大单调递减；当π/6<φ≤π/3或π/2<φ<2π/3时，输入侧电流THD随φ的增大单调递增；在φ为0、π/3、2π/3时，输入侧电流THD取得最大值(约为30.9%)；在φ为π/6、π/2时，输入侧电流THD取得最小值(约为15.0%)。

2.2 移相角对输出侧电压的影响

图1中，根据调制原理，两整流桥输出电压可表示为

(12)

式中：sa1(t)、sa2(t)、sb1(t)、sb2(t)、sc1(t)、sc2(t)分别为a1、a2、b1、b2、c1、c2的映射函数。表达式分别为

(13)

从图1中可得负载电压ud为

ud=(ud1+ud2)/2

(14)

定义负载电压纹波系数K为

(15)

式中：udmax、udmin、udav分别为负载电压的最大、最小、平均值。

利用Matlab编程将式(13)代入式(12)中，再将式(12)代入式(14)中可求得ud。求得ud的udmax、udmin和udav，将udmax、udmin和udav值代入式(15)，可得φ与K之间的关系曲线，见图5。

图5中，当0<φ≤π/6或π/3<φ≤π/2时，K随φ的增大单调递减；当π/6<φ≤π/3或π/2<φ<2π/3时，K随φ的增大单调递增；在φ为0、π/3、2π/3时，K取得最大值(约为0.070)；在φ为π/6、π/2时，K取得最小值(约为0.017)。

3 移相角对整流系统磁性器件的影响

图1整流系统磁性器件包括多边形AT、IPR及ZSBT。

3.1 移相角对多边形AT等效容量的影响

设原边绕组和次边绕组电压的有效值分别为UY和US，从图3可得

(16)

(17)

由磁动势平衡方程得为

i1=

(18)

(19)

(20)

多边形AT容量S表达式为

(21)

式中：I1、I2、I3分别为i1、i2、i3的方均根值。

输出功率P0为

P0=UdId

(22)

式中：Ud为ud的方均根值；Id为负载电流id方均根值。

定义AT等效容量Seq为

(23)

利用Matlab编程，由式(18)～式(20)和式(14)可得i1、i2、i3和ud对应方均根值I1、I2、I3和Ud。将I1、I2、I3和式(16)、式(17)代入式(21)可得S，将Id设为常数，由式(22)可求得P0，将P0和S代入式(23)，可得φ与Seq之间的关系曲线，见图6。

图6中，随着φ的增大Seq呈单调上升趋势；在φ为0时Seq取得最小值(约为0.0%)；在φ为2π/3时Seq取得最大值(约为90.6%)；在φ为π/6、π/2时，Seq值分别约为18.2%、62.8%。

3.2 移相角对IPR和ZSBT等效容量的影响

从图1分析可得

uIPR=ud1-ud2

(24)

IPR容量SIPR表达式为

(25)

式中：IIPR为IPR上过电流iIPR的方均根值。在大电感负载条件下，iIPR为负载电流的一半。

定义IPR等效容量SeqIPR为

(26)

利用Matlab编程，将式(13)代入式(12)，求得ud1和ud2。将ud1和ud2代入式(24)可得uIRP。求得uIPR对应方均根值UIPR。将Id设为常数，将UIPR和IIPR代入式(25)可得SIPR。同上可得P0，将SIPR和P0代入式(26)可得φ与SeqIPR间的关系曲线，见图7。

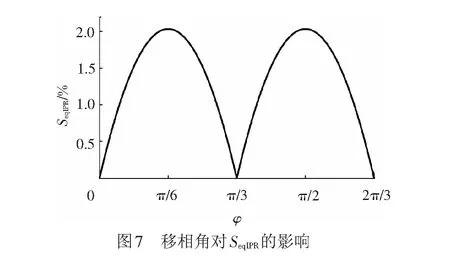
图7中，当0<φ≤π/6或π/3<φ≤π/2时，SeqIPR随φ的增大单调递增；当π/6<φ≤π/3或π/2<φ<2π/3时，SeqIPR随φ的增大单调递减；在φ为0、π/3、2π/3时，SeqIPR取得最小值(约为0.0%)；在φ为π/6、π/2时，SeqIPR取得最大值(约为2.0%)。

在图1中假设2个点m2和m4处对n点电位分别是vm2n和vm4n，则

(27)

(28)

其中，i=a、b、c。

结合图3则

(29)

ZSBT容量SZSBT表达式为

(30)

式中：IZSBT为ZSBT上流过电流iZSBT的方均根值;UZSBT为电压uZSBT的方均根值。在大电感负载条件下，iZSBT为负载电流的一半。

定义ZSBT等效容量SeqZSBT为

(31)

利用Matlab编程，由式(13)、式(27)、式(28)求得vm2n和vm4n，将vm2n和vm4n代入式(29)，求得uZSBT及UZSBT。将UZSBT和IZSBT代入式(30)可得SZSBT。同理可得P0。将SZSBT和P0代入式(31)可得φ与SeqZSBT之间的关系曲线，见图8。

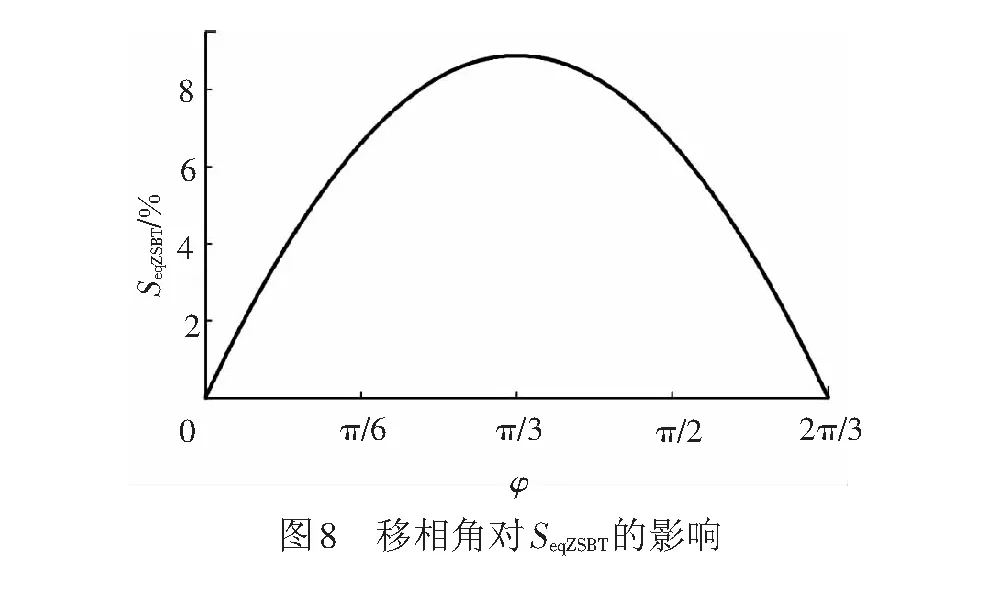
图8中，当0<φ≤π/3时，SeqZSBT随φ的增大单调递增；当π/3<φ<2π/3时，SeqZSBT随φ的增大单调递减；在φ为0、2π/3时，SeqZSBT取得最小值(约为0.0%)；在φ为π/3时，SeqZSBT取得最大值(约为8.9%)；在φ为π/6、π/2时，SeqZSBT均约为6.6%。

4 仿真验证

在Matlab中搭建的仿真电路图见图9。

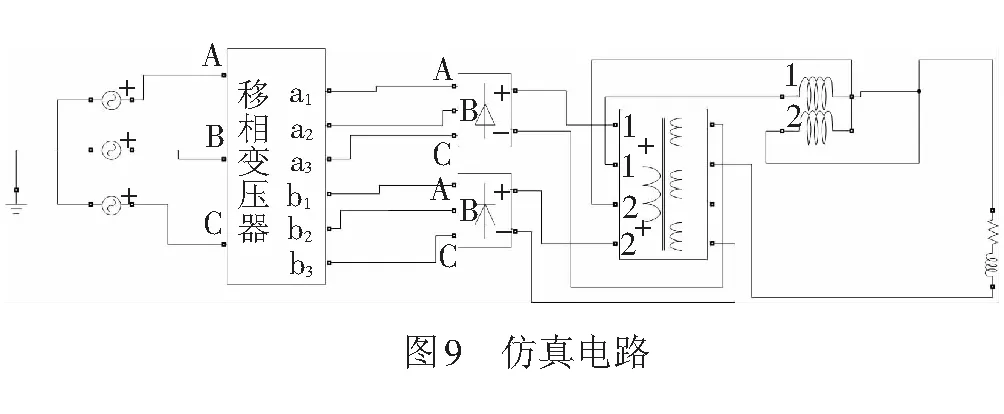
图9中，多边形AT、ZSBT、IPR和负载从左到右依次连接，其中变压绕组联结部分已封装。整流桥采用二极管整流。采样时间为0.02 ms。

4.1 移相角对整流系统运行参数的影响

φ与输入线电流THD仿真曲线与理论曲线比较见图10(a)。图10(a)中仿真曲线和理论分析曲线的变化趋势基本一致；仿真结果中，输入侧电流THD在φ接近0、π/6、π/3、π/2、2π/3时，分别为29.85%、14.35%、28.85%、14.35%、29.85%，与各自理论值基本一致。

φ与负载电压纹波系数仿真曲线与理论曲线比较见图10(b)。图10(b)中，仿真曲线和理论分析曲线的变化趋势基本一致；仿真结果中，K在φ接近0、π/6、π/3、π/2、2π/3时，分别为0.069 4、0.018 6、0.071 6、0.018 6、0.069 4，与各自理论值基本一致。

4.2 移相角对整流系统磁性器件的影响

φ与Seq仿真曲线与理论曲线比较见图11(a)。图11(a)中，仿真曲线和理论分析曲线的变化趋势基本一致；仿真结果中，Seq在φ为π/6、π/2时，分别为18.89%、66.36%，与各自理论值基本一致。

φ与SeqIPR仿真曲线与理论曲线比较见图11(b)。图11(b)中，仿真曲线和理论分析曲线的变化趋势基本一致；仿真结果中，SeqIPR在φ接近0、π/6、π/3、π/2、2π/3时，分别为0.25%、2.14%、0.13%、2.14%、0.25%，与各自理论值基本一致。

φ与SeqZSBT仿真曲线与理论曲线比较见图11(c)。

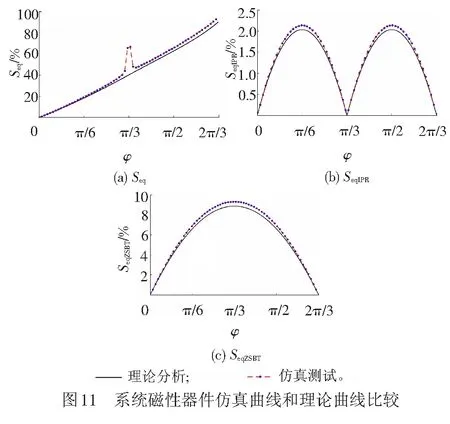
图11(c)中，仿真曲线和理论分析曲线的变化趋基本一致；仿真结果中，SeqZSBT在φ接近0、π/6、π/3、π/2、2π/3时，分别为0.55%、6.87%、9.33%、6.87%、0.55%，与各自理论值基本一致。

5 结论

综上所述，可得以下结论：

(1) 当0<φ≤π/6或π/3<φ≤π/2时，输入侧电流THD及负载电压纹波系数均随φ的增大单调递减；当0<φ≤π/6或π/3<φ≤π/2时，输入侧电流THD及负载电压纹波系数均随φ的增大单调递增；输入侧电流THD及负载电压纹波系数均在φ为0、π/3、2π/3时，取得最大值，在φ为π/6、π/2时，取得最小值。故升压移相角应从π/6、π/2中选取。

(2) 随着φ的增大Seq呈单调上升趋势，在φ为0时取得最小值，在φ为2π/3时取得最大值；当0<φ≤π/6或π/3<φ≤π/2时，SeqIPR随φ的增大单调递增，当π/6<φ≤π/3或π/2<φ<2π/3时，SeqIPR随φ的增大单调递减，在φ为0、π/3、2π/3时，SeqIPR取得最小值，在φ为π/6、π/2时，SeqIPR取得最大值；当0<φ≤π/3时，SeqZSBT随φ的增大单调递增，当π/3<φ<2π/3时，SeqZSBT随φ的增大单调递减，在φ为0、2π/3时，SeqZSBT取得最小值，在φ为π/3时，SeqZSBT取得最大值。