基于非线性超声的无缝钢轨锁定轨温检测

2020-04-16牛笑川朱力强余祖俊

铁道学报 2020年3期

牛笑川, 朱力强, 余祖俊

(1. 北京交通大学机械与电子控制工程学院，北京 100044；2. 北京交通大学载运工具先进制造与测控技术教育部重点试验室，北京 100044)

无缝钢轨能够有效减少列车运行过程中受到的振动冲击，降低运行噪声，提高列车运行平稳性，现已被广泛应用于高速铁路、地铁以及重要干线铁路中。无缝钢轨在轨温发生变化时，由于没有轨缝而不能伸缩，其内部会产生纵向温度应力。无缝钢轨的锁定轨温是指无缝钢轨内部纵向温度应力为0时的温度，也叫做无缝钢轨的零应力轨温。一般来说，轨温的变化范围远大于环境温度变化范围，例如在中国华北地区，轨温变化范围接近100 ℃。如果以60 kg/m钢轨为例，轨温相对于锁定轨温每变化1 ℃，线路固定区内钢轨纵向温度应力变化达2.43 MPa[1]。因此，夏季无缝钢轨内压应力容易过大，诱发胀轨、跑道；冬季无缝钢轨拉应力容易过大，诱发断轨，这些都直接威胁列车运行安全。进而需要一种能够准确在线监测无缝钢轨内部纵向温度应力的方法，在应力超过安全阈值前及时预警，这对于保证轨道结构性能及列车运行安全有着重要意义。

理论上，如果能够准确测得钢轨的锁定轨温，根据胡克定律即可计算得到钢轨纵向应力

σ=Eα(T-T0)

( 1 )

式中：σ为钢轨纵向应力;E为杨氏模量;α为钢轨线性热膨胀系数;T为钢轨温度;T0为钢轨锁定轨温。

现有成熟的钢轨温度应力在线监测技术主要基于应变法[2-3]，即在钢轨初始应力或锁定轨温已知的条件下，通过测量钢轨的温度应变量来测得钢轨的相对温度应力。但锁定轨温在钢轨长期服役过程中常常会发生漂移，导致这种方法并不可靠。文献[4-5]提出了提拉钢轨法、文献[6]提出了横向位移法，都实现了钢轨温度应力的测量，但是这些方法都需要在天窗时间、解除一定长度的扣件约束且钢轨处于拉应力状态时才能进行。国内外学者也对应用巴克豪森噪声[7]、X射线[8]、临界角折射超声体波[1，9]等原理的无损检测方法进行了理论和试验研究，但均未能很好解决钢轨表面残余应力对监测结果影响的问题。由于对应力敏感、传播时能够引起整个横截面质点振动、受钢轨表面残余应力影响较小等优点，超声导波近年来已经成为检测钢轨纵向温度应力的研究热点[10-13]，但这种利用声弹性原理的线性超声检测技术仍受钢轨材质差异、温度变化及磨耗等因素影响较大。因此，无缝钢轨纵向温度应力监测仍然是一个看似简单却又难以解决的技术性难题。

本文主要研究基于非线性超声原理的钢轨温度应力检测技术，通过监测非线性系数的变化在线识别钢轨锁定轨温，可以避免线性超声检测理论所面临的技术难题。论文首先理论分析了非线性系数随温度与应力的变化规律，然后比较了钢轨在自由和锁定状态下，超声非线性系数的实物测试结果，验证了理论分析的正确性。论文研究成果对于钢轨温度应力检测新技术研究有重要的参考价值。

1 非线性系数的温度敏感性问题

大振幅超声波在结构中传播时与介质或损伤发生相互作用并表现出非线性特征，具体表现形式为超声波在传播过程中除原有基频信号还会产生高次谐波信号。非线性超声技术应用声学手段提取信号中的高次谐波，通过计算特有的非线性系数实现对结构内部状态及损伤的量化、监测及性能评价，现已广泛应用于检测材料内部拉伸(压缩)塑形损伤[14-15]、循环荷载下结构的疲劳损伤[16-17]、材料高温的蠕变损伤[18]、复合材料黏合面的缺陷检测[19]、结构早期微裂纹检测[20]等无损领域，并取得了较好的研究成果，这为无缝钢轨内温度应力检测问题提供了一种解决方法。

文献[21]通过试验得到温度对固体中传播的纵波非线性系数变化没有影响的结论，因此认为无缝钢轨中传播的超声非线性系数如果发生变化完全是由内部应力变化引起的。在此基础上，文献[22]试验研究发现无缝钢轨中传播超声的非线性系数随钢轨内部温度应力改变而变化，并在钢轨处于零应力状态，即钢轨温度为锁定轨温时处于局部极值点。因此，可以通过监测非线性系数的变化确定钢轨锁定轨温和应力状态。

文献[23]对板状结构进行加热，观察板中传播的超声非线性系数变化，发现温度对超声非线性现象存在影响，这与文献[21]的试验结果相互矛盾。文献[24]重复了文献[21]的相关试验，研究发现无应力状态下固体中传播的超声非线性系数随温度升高而增大，温度对固体中超声非线性有明显影响。文献[21]也缺少固体中超声非线性系数在单纯温度作用下变化情况的理论推导，其试验对象是钢块，试验结果也不一定适用于无缝钢轨这类结构。

综上所述，现有应用非线性超声检测无缝钢轨温度应力的研究还处于理论及试验研究阶段，有关温度与应力对钢轨超声非线性影响的研究开展较少，缺少理论推导及以钢轨为试验对象的验证试验。而钢轨在服役过程中温度变化范围较大，温度可能影响超声非线性现象中的高次谐波幅值，进一步造成试验结论的偏差，所以有必要深入研究温度及应力对钢轨中传播的超声非线性系数的影响规律。同时，如果温度与应力对材料非线性存在影响，应用非线性超声是否能够确定无缝钢轨锁定轨温有待理论分析及试验验证。

因此，本文通过理论推导得到材料非线性系数在温度与应力变化过程中的变化规律，明确了温度及应力对材料非线性有明显影响，钢轨中超声非线性系数在温度与应力作用下呈V形变化。进一步以无缝钢轨为试验对象搭建了无缝钢轨温控箱开展相关试验，通过温控设备对自由状态及锁定状态下钢轨施加温度影响，检测并比较了两种状态下钢轨中传播的超声非线性系数随温度的变化情况，验证了理论推导的正确性。通过模拟无缝钢轨在线服役过程中内部温度应力变化情况，试验证明了钢轨中传播的超声非线性系数在钢轨零应力状态时出现极值点，可以应用非线性超声检测无缝钢轨锁定轨温。

2 非线性系数变化规律分析

结构材料基本状态(例如温度、应力等)对非线性超声的影响规律研究属于经典非线性问题，而固体介质的经典非线性主要源于材料介质晶体结构及内部微缺陷，可以通过非线性系数加以描述评价。文献[25]通过位错偶模型推导出固体内部应变表达式

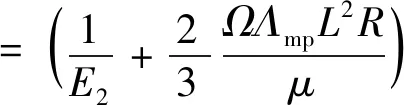
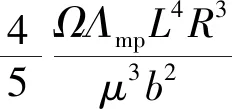
( 2 )

式中：E2、E3分别为材料二阶、三阶弹性模量;Ω、R为剪应力与正应力之间转换系数；Λmp为单极位错密度；L为位错弦长；μ为材料剪切模量；b为Burgers矢量。以上均为与材料相关的常数；ε为固体由于受到应力作用发生的应变；σ为固体受到的应力，因为只考虑二次非线性，所以只考虑到σ的三次项。

固体受到应力σ是与固体应变ε有关的函数，在ε=ε1处应用泰勒级数将应力σ表达式展开，可得

( 3 )

式中：ε1为固体某一时刻应变;σ1为ε=ε1时固体所受应力;β为固体材料非线性系数。

( 4 )

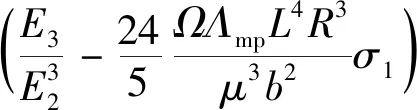
( 5 )

( 6 )

分别定义

( 7 )

( 8 )

则固体材料非线性系数可以表示为

β=βl+βd

( 9 )

实际上βl表示由于固体晶格固有非谐性相关产生的材料非线性系数，与材料的二阶、三阶弹性模量相关。固体受到外部作用力时，内部微观结构常伴有位错运动的发生，位错也会造成非线性系数的变化，用βd表示，βd与材料所受应力相关。

当金属材料在温度不变状态下只受应力作用影响时，由于材料弹性模量变化主要受温度影响，所以βl没有变化，材料超声非线性系数的变化量主要体现在βd的变化上，当金属材料受到拉应力或压应力作用时，βd随拉应力或压应力的增加而增大，最终导致材料超声非线性系数随材料所受拉应力或压应力的增加增大，文献[26-27]进行了相关试验研究，得到了类似的试验结果。

当金属材料在零应力状态下只受温度作用影响时，βd为0，固体相对超声非线性系数由βl组成，当金属材料温度变化时，材料二阶、三阶弹性模量会随温度的升高而减小，选取铁在温度为-20～60 ℃时的二阶、三阶弹性模量值[28-29]，见表1。

代入式( 7 )分别计算不同温度下超声非线性系数，结果见图1。

由图1可以看出，当金属材料只受温度影响时，材料非线性系数随温度升高而增大，随温度降低而减小。

无缝钢轨在实际线路中受到温度与应力的耦合作用，为了计算超声非线性系数在不同温度与应力条件下的值，进行如下取值[30]：取Ω=R=0.33，Λmp=0.658×1014m-2，L=196 nm，Burgers矢量的大小为b=2.5 nm，σ由式( 1 )计算得到，α=11.5×10-6/℃，锁定轨温T0=20 ℃，T=-20～60 ℃，E2、E3取值见表1，分别代入式( 7 )计算非线性系数，结果见图2。

表1 铁的二阶、三阶弹性模量随温度变化值

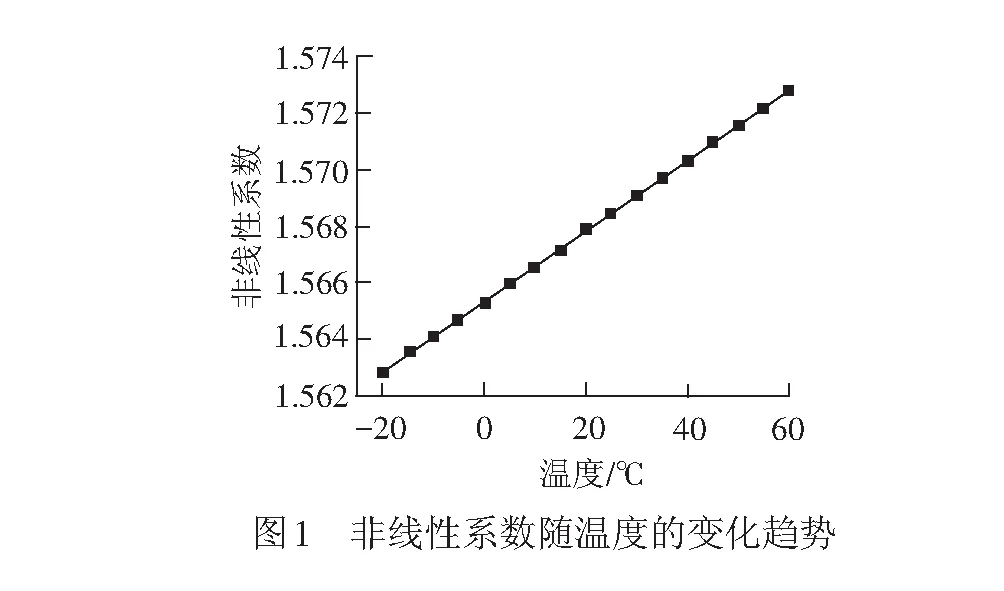
由图2可以看出：

(1) 当无缝钢轨温度高于锁定轨温(T0=20 ℃)并持续升高时，非线性系数随温度升高持续增大。这是由于此时钢轨内部压应力随温度升高而增大，根据式( 8 )，βd随内部压应力的增加而增大，而由上面的讨论已经知道βl随温度的升高而增大(见图1)。因此，锁定状态下的非线性系数随温度的增加而增大。

(2)当钢轨温度低于锁定轨温并持续降低时，非线性系数随温度降低而增大。这是由于钢轨处于拉伸状态，钢轨内部拉应力随温度降低而增大。虽然βl随温度降低而减小，βd随内部拉应力增加而增大，但是由于数值上βd远大于βl，最终导致非线性系数随温度降低持续增大。因此，在整个温度变化过程中，钢轨内非线性系数在应力与温度耦合作用下呈V型变化，只有当钢轨温度为锁定温度时，即钢轨内应力为0时，非线性系数会出现局部极小值点。从以上理论分析可知，通过连续监测无缝钢轨非线性系数和轨温的变化情况，测量钢轨温度呈单调变化、但非线性系数出现局部极小值时的钢轨温度，即可得到无缝钢轨锁定轨温。

由于材料非线性系数试验测量非常困难,试验中需要用便于检测的测量值来表征材料非线性系数。文献[25]根据原子晶格原理建立了三维模型，推导出固体介质中传播的非线性超声波动方程

( 10 )

式中：u为由超声波传播引起的质点位移;t为传播时间;c为超声波在固体内传播的波速;x为材料坐标。

由于式(10)无精确解析解，在非线性声学中一般采用逐级近似的方法来求解其近似解，假设式(10)的解为[24]

u(x,t)=u(0)+βu(1)

(11)

式中:u(0)、u(1)分别为材料线性和非线性位移，u(0)>>βu(1)。

将式(11)代入式(10)中，整理化简并略去β高次项后得到

(12)

设线性位移满足

u(0)(x,t)=A1cos(ωτ)

(13)

式中：A1为超声激励信号幅值;τ=t-x/c;ω为角频率,ω=kc;k为波数。

将式(13)代入式(12)，得到一个非齐次方程，令

u(1)(x,t)=xfτ

(14)

将式(14)也代入式(12)并求解，解得

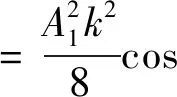
(15)

则得到式(10)的逐级近似解为

u(x,t)=u(0)+βu(1)=

(16)

由式(16)可见，角频率为ω的超声波在非线性固体介质中传播时发生了变形，除角频率为ω的基波分量外，还产生了角频率为2ω的高次谐波，以A(ω)、A(2ω)分别为基波和二次谐波引起的材料质点振动幅值，定义固体中传播的超声非线性系数[25]

(17)

式(17)表明，当试验条件确定后，A(2ω)与A(ω)平方的比值与材料非线性系数直接相关,可以将超声非线性系数作为材料非线性系数的测量值。

通常试验中以接收信号的基频信号幅值与二倍频信号幅值代替A(ω)和A(2ω)，而基频信号与二倍频信号幅值与换能器的接收响应直接相关，定义固体的相对超声非线性系数作为非线性系数试验测量值，即

(18)

式中:γ1、γ2为压电超声换能器关于基频信号与二倍频信号幅值的标定系数，与换能器受温度影响情况、换能器与试件接触情况、放大器放大倍数等有关，在试验中主要受温度影响；γ1A(ω)、γ2A(2ω)分别为试验测量系统采集信号的基频幅值与二倍频幅值。

3 自由状态钢轨非线性超声试验

为了进一步证实理论推导结果，分别以自由状态及约束状态下钢轨为试验对象进行如下相关验证试验。搭建大型钢轨温控试验平台，试验平台按实际无砟轨道线路等比例建造，试验平台所用钢轨型号为60 kg/m，长度为7 m，钢轨垂向通过底部扣件进行约束，钢轨上方有圆柱横梁，防止钢轨受力过程中翘起，钢轨一端与平台底座相连接，另一端通过钢轨夹持机构施加纵向约束。当钢轨夹持机构没有锁死，同时解除钢轨底部扣件约束时，钢轨处于自由状态，在温度变化过程中钢轨能够自由伸缩，钢轨中传播的超声非线性只受温度影响。钢轨底部约束见图3(a), 钢轨夹持机构见图3(b)。试验通过温控箱对钢轨施加温度影响，钢轨温控箱见图3(c)，试验采用RITEC RAM-5000高能超声测试系统对超声换能器进行信号激励与接收，见图3(d)。未加盖温控箱的钢轨试验平台见图3(e)，钢轨温控平台结构原理见图3(f)。

超声换能器与钢轨一同放置在温控箱中，实验室室温为20 ℃，试验过程中钢轨温度变化范围为-20～60 ℃。由于温度变化会改变常规耦合剂的黏稠度，直接导致超声进入固体中的信号幅值和接收信号幅度发生变化，最终导致接收信号的信噪比变化。因此，在试验中换能器与钢轨之间采用AB胶充当耦合剂，与采用常规耦合剂相比，固化后的AB胶没有黏稠度，会导致接收到的信号幅值较小，但在温度变化过程中AB胶对超声波的耦合效果基本不变，可以有效消除试验中接收信号信噪比的波动。同时，试验选用PAC公司R15α、R6α压电超声换能器，换能器正常工作温度范围为-65～105 ℃，试验中温度对换能器的影响几乎可以忽略不计。试验系统的测试原理见图4。

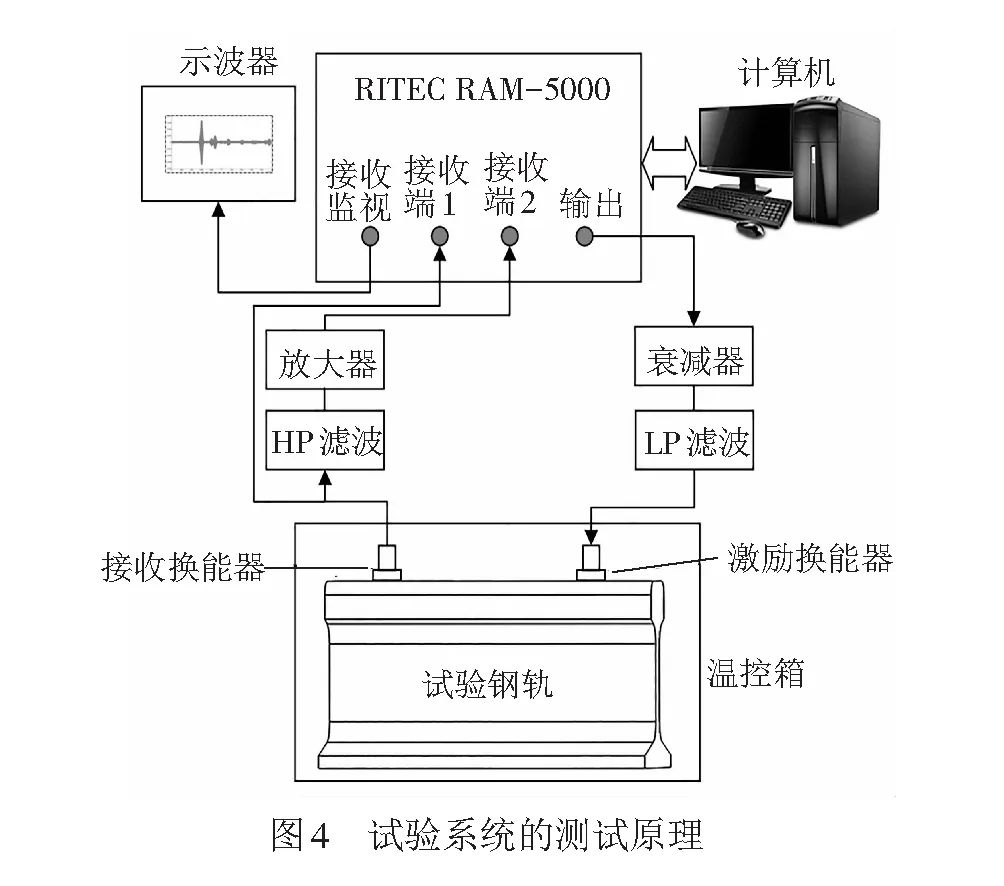
试验中激励换能器与接收换能器均布置在钢轨轨头中央，相距35 cm。激励信号采用中心频率为80 kHz、汉宁窗调制的10周期正弦波脉冲信号，激励波形见图5。入射波包在传播过程中，经过钢轨外截面发生多次反射与波形转换，在传播方向上形成多个波包，换能器接收波形见图6。试验选取接收信号的第一个波包(图6圆圈内部分)进行快速傅里叶变换(FFT)，提取基频与二次谐波信号，计算非线性系数。由接收信号的频谱分析图可以看到有明显的二次谐波存在，见图7。

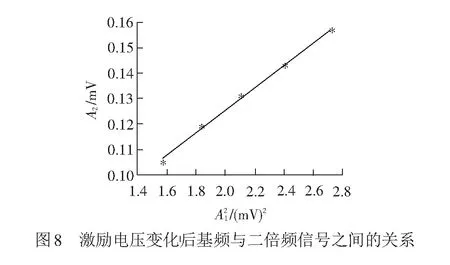
在计算非线性系数之前，需要将激励信号幅值逐渐增大，在每个激励幅值下，提取相应的基频信号与二次谐波信号幅值，观察二次谐波幅值与基频信号幅值平方关系的变化情况，见图8。由图8可以看出，随着激励电压的增加，二次谐波幅值与基频信号幅值的平方之间存在良好的线性关系，因为系统电信号的基频幅值和高阶谐波幅值之间只存在简单的线性关系,不存在平方或立方等关系[31]，所以接收到的二次谐波信号是钢轨自身非线性造成的，而不是检测系统产生的非线性和线性信号产生的伪信号。

为了进一步减小温度对信号传输的影响，应用RITEC RAM-5000高能超声测试系统对信号进行750次/min并计算非线性系数，钢轨温度每改变1 ℃平均需要1 h。试验中钢轨温度每变化5 ℃时，测试系统采样200次，这段时间内接收到的信号反映的是该温度下钢轨的非线性状态，信号相对稳定。计算各个温度下非线性系数的均值与方差，得到自由状态钢轨中超声非线性系数随温度的变化曲线，重复试验3次，试验结果重复性良好，结果见图9。

由试验结果可见，自由状态钢轨中传播的超声非线性系数随钢轨温度升高而逐渐增大，随钢轨温度降低而逐渐减小，与理论推导结果一致，证明了温度对自由状态下钢轨中传播的超声非线性存在明显影响。因此，在应用非线性超声检测无缝钢轨中温度应力时，不能简单排除温度对超声非线性系数变化的影响。

4 锁定状态钢轨非线性超声试验

为了模拟实际线路中无缝钢轨内部温度应力的变化情况，在钢轨温度为20 ℃时，通过夹持机构对温控箱内钢轨两端施加约束，使钢轨两端固定，同时锁紧钢轨底部扣件，此时钢轨的锁定轨温为20 ℃，钢轨内无应力作用。进一步通过温控箱对锁定状态下钢轨施加温度影响，在温度变化过程中钢轨不能自由伸缩，钢轨中传播的超声非线性受到温度与应力的耦合影响。

试验中钢轨温度变化设定、换能器布置位置、激励信号选取均与自由状态下钢轨非线性超声试验一致。计算温度变化过程中非线性系数的均值与方差，得到锁定状态下钢轨中超声非线性系数随温度的变化曲线。改变钢轨锁定轨温，分别在钢轨温度为15、25 ℃时重新锁定并进行试验，试验结果见图10。

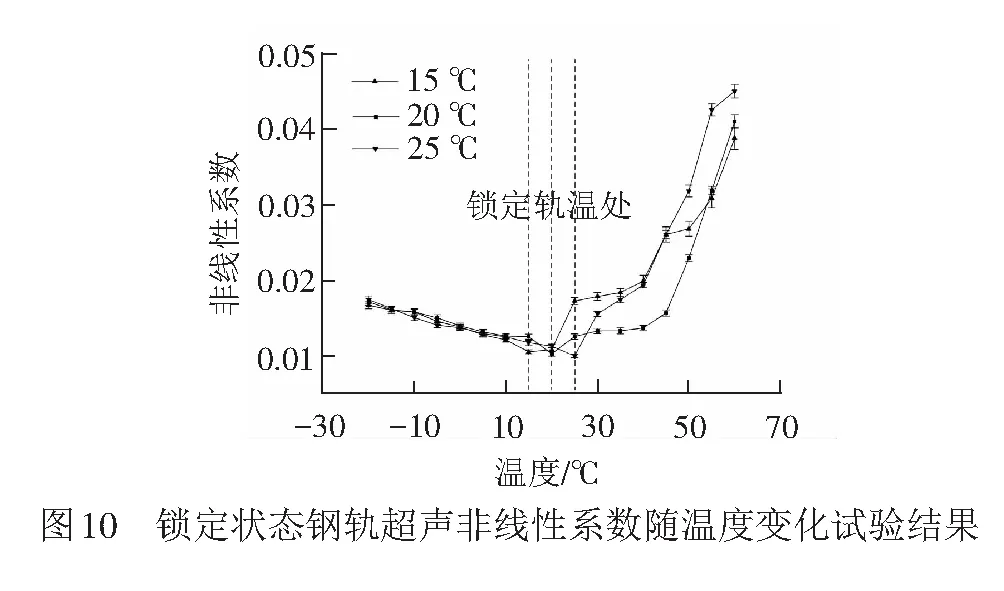
试验结果表明，锁定状态下钢轨中传播的超声非线性系数受到温度与应力共同作用的影响，随温度与应力的变化发生改变。当钢轨温度偏离锁定轨温时，在升温与降温阶段非线性系数均持续增大，在整个温度变化过程中，非线性系数呈V型变化，在锁定轨温处出现极小值，试验结果与理论推导结果一致。从图10还可以发现，在3个锁定轨温的试验中，钢轨温度为锁定轨温时的非线性系数都小于锁定轨温±5 ℃以外温度点的非线性系数，因此锁定轨温的估计误差在±5 ℃以内。由于试验中采用的压电换能器外表面为金属，压电换能器与钢轨在温控箱中，在升温过程中会由于温度的升高导致内部压电片振动稳定性减弱，最终导致试验结果中偏离锁定轨温的升温阶段与降温阶段在非线性系数数值上没有对称性，同时3次试验升温阶段非线性系数变化波动较大，但不影响非线性系数的变化趋势和论文的主要结论。

需要说明的是，非线性超声试验将超声信号二倍频幅值与基频幅值平方的比值作为超声非线性系数测量值，超声非线性系数的灵敏度极高，任何超声探头在结构上微小的位移都会直接影响最终信号各频率成分幅值的大小，进而改变最终测量值结果，所以重复非线性超声试验中超声非线性系数的绝对值是不同的。但在超声探头固定后，测得的超声非线性系数的绝对值具有很好的重复性，因此超声非线性系数的相对变化趋势可以有效反映被测结构内部状态及损伤等的变化情况。目前国内外非线性超声试验[14-24]都将超声非线性系数的相对变化值作为观测指标，难以做到应用超声非线性系数的绝对值。同时，由于结构服役过程中内部材料非线性系数绝对值也是在缓慢变化的，因此通过监测超声非线性系数的绝对值来感知应力、疲劳损伤等的意义不大。本文试验分析时，应力、温度综合影响与单纯温度影响下的超声非线性系数值在同一量级，部分数据甚至还略小，其原因也是由于完成单纯温度试验后，换能器进行了重新粘贴，接收与激励探头的位置发生了微小变化。本文提出的方法是通过观察超声非线性系数在温度与应力综合作用下的相对变化值来确定无缝钢轨锁定轨温，不受绝对值问题的影响。