基于Sobol’法的轨道车辆前端吸能结构灵敏度分析

陈秉智，汪驹畅,2

(1. 大连交通大学 机车车辆工程学院， 辽宁 大连 116028；2. 中车青岛四方机车车辆股份有限公司 转向架分厂， 山东 青岛 266111)

轨道交通在我国交通运输中一直扮演着重要的角色。但由于其运行速度高、质量大、盲点多的特点，如果发生交通事故所产生的后果必然十分严重，所以提高轨道车辆车体结构耐撞性尤为重要。而影响车体结构耐撞性的设计参数众多，因此很有必要通过灵敏度分析辨别其中的关键参数，简化优化模型[1]。吸能结构的灵敏度可定义为吸能结构各参数发生变化时，对耐撞性能的影响程度。

灵敏度分析方法大致可以分为局部灵敏度分析法和全局灵敏度分析法。其中局部灵敏度分析法依靠线性模型的基础发展起来，因此，当研究非线性问题、或者输入变量的不确定性在不同的数量级时，局部灵敏度分析很难提供有效的结果，并且无法考虑多个变量共同作用时各变量之间的交互作用对结果的影响[2]。而全局灵敏度分析法允许各参数同时变化，且能分析多个参数交互效应的灵敏度。全局灵敏度分析包括回归法、方差法和Sobol’法等。其中Sobol’法基于方差分析全局灵敏度,通过计算各因素的输入对输出方差的影响,评估单个以及多个因素交互效应的灵敏度。Sobol’法形式简单,计算方便,特别是当模型无确定的函数表达时,可以采用蒙特卡洛方法或Kriging代理模型近似计算[3]。于德介等[4]以线性阻尼、立方刚度的非线性被动隔振体为对象, 用Sobol’法计算得出了软、硬弹簧和线性阻尼对传递率的影响规律。张小丽等[5]使用Sobol’法分析了新安江三水源模型的参数灵敏度, 结果表明Sobol’法得到的敏感度适合多目标间的对比。陈静等[6]用通过构造双层底板架结构强度和稳定性的Kriging代理模型，对双层底板架结构各设计变量对板架强度和稳定性响应指标进行了全局灵敏度分析。邵永生等[7]将Sobol’法用于Sperling指标的全局灵敏度分析,得到各个参数对车辆平稳性指标的一阶灵敏度及总灵敏度。聂祚兴等[8]将Sobol’全局灵敏度分析法引入到汽车噪声传递函数的灵敏度分析中，有效避免了局部灵敏度分析方法的缺陷。陈刚等人[9]采用Sobol’法对冲击载荷作用下的二维管路系统材料的弹性模量、密度、管壁厚、内径,支承刚度及位置及冲击作用间隔时间等参数进行了全局灵敏度分析,甄别出影响管路系统冲击动响应的关键参数。于德介等人[10]将基于方差的Sobol’全局灵敏度方法引入结构动力分析中，计算了传递率对结构参数的一阶及总灵敏度 ,其结果为系统的优化设计提供依据。

但在轨道车辆领域，尤其耐撞性研究中，该方法应用较少。本文针对某地铁车辆司机室前端吸能结构的众多设计参数，采用Sobol’法进行灵敏度分析。同时考虑到碰撞过程参数间无准确关系函数以及计算新样本较为耗时的特点，无法使用公式法和蒙特卡罗积分法进行计算。因此，本文通过构建具有较高拟合精度的Kriging代理模型求解Sobol’指数，分析各参数的一阶主灵敏度值、总灵敏度值及二阶交互效应灵敏度。结果有助于理解不同的输出响应对各参数及参数间相互作用的敏感性，识别对耐撞性能产生主要影响的设计参数，为吸能结构优化设计提供有力参考。将复杂模型合理简化，提高优化效率。

1 Sobol’全局灵敏度分析法原理

Sobol’全局灵敏度分析法认为目标的总方差是由单个参数产生的方差和参数间的相互作用产生的方差叠加而成的[11]。所以其核心思想就是将函数f(X)分解为如下形式

…+f1,2,…,n(x1,x2,…,xn)

( 1 )

式中：f0为常数项；xi、xj为不同的变量；n为变量总数；X为所有变量组成的向量；fi(xi)为函数中只含有单变量的部分；fi,j(xi,xj)为函数中双变量部分，以此类推。

为保证分解形式的惟一性和可求性，规定右边每一项对其所包含的任一变量的积分为零，因此方程右边各项前三项可以表达为式( 2 )～式( 4 )。

( 2 )

( 3 )

fi,j(xi,xj)=

( 4 )

式中：i、j、k为设计变量编号。式( 1 )中右边其他子项均可由此类推得到。

Sobol’法的总方差V是由所有输入参数产生。

( 5 )

由单个参数影响产生的偏方差Vi为

( 6 )

由参数间交互效应产生的偏方差Vi1,i2,…,is可以表达为

( 7 )

因此，将方差的比值定义为参数的Sobol’灵敏度指数，该数值的大小表示对输出结果的影响程度。Sobol’灵敏度指数Si1,i2,…,is为

( 8 )

式中：s为设计参数个数。 然而有时关系函数很复杂，比如轨道列车吸能结构的碰撞过程，很难找到准确的关系函数表达，无法通过上述公式求得Sobol’指数，只能根据样本点近似求解。

较为常用的基于样本点的求解方法是蒙特卡洛积分法和Kriging代理模型法。其中蒙特卡罗积分法通过构建2个N·s的矩阵A、B(N为规定的样本数)及分别交换各列得到2s个新矩阵作为输入矩阵，计算总方差与偏方差，进而求得Sobol’指数。这种方法计算较为简便，但其精度受采样方式及样本数量N直接影响，且需要重新计算的样本点个数为N·2(s+1)，在计算本就十分耗时的耐撞性分析中不太实用。因此，本文采用Kriging代理模型法求解Sobol’指数。

1.1 Kriging模型求解Sobol’指数

Kriging代理模型最早应用于地质学中，确定矿物的储量，而后逐渐发展形成了完善的系统理论。Kriging模型主要借助附近的已知点而对某一点进行模拟，通过一定范围内的已知信息，基于最小化误差的方差，选择加权线性组合来估计[12]。Kriging模型一般由回归模型和随机部分组成，具体形式为

y(X)=gT(X)β+z(X)

( 9 )

式中：β为回归参数；gT(X)为回归模型，通常是多项式函数，为模型提供全局近似；z(X)为随机部分，服从正态分布N(0,σ2)，为模型提供局部近似。z(X)的协方差矩阵Cov|z(xi,xj)|可以表达为

Cov|z(xi,xj)|=σ2|R(xi,xj)|

(10)

式中：R(xi,xj)为任意2个样本点空间相关性函数，对模拟的精度起决定性作用。一般可选择线性方程、指数方程、高斯方程、三次样条等。其中计算效果最好、被广泛应用的是高斯方程。

相比于传统的差值技术，Kriging代理模型根据已有样本进行构造时充分考虑了空间上的相关特征，仅依靠待估点周围的已知样本，而非一律使用所有样本进行拟合，这使得Kriging模型兼具全局性和局部性[13]，可以动态的反应参数间关系。

1.2 数例分析

为验证Kriging代理模型法近似求解Sobol’指数的实际效果，下面对一个三元非线性函数进行参数t1、t2和t3的灵敏度计算。

y=3et1+2sint2+t1t2t3

t1,t2,t3∈[1,2]

(11)

Kriging模型采用Latin超立方采样，二次回归函数，高斯相关方程。计算的Sobol’指数见表1。

表1 估算灵敏度值与真实值对比

由表1可看出，Kriging代理模型法计算的Sobol’指数与公式法求得的真实值十分接近，达到了较高的精度。故该方法可用于吸能结构全局灵敏度分析中近似求解Sobol’指数。

2 吸能结构全局灵敏度分析

2.1 车辆耐撞性仿真分析

车辆碰撞是一个瞬态的复杂物理过程，它包括以大位移、大转动和大应变为特征的几何非线性，以材料弹塑性变形为典型特征的材料非线性和以接触摩擦为特征的边界非线性[14]。目前，在国内外广泛用于大变形碰撞问题的主要应用软件均基于动量方程、质量方程、能量守恒方程、边界约束方程等[15]，且大多采用时间域的显式中心差分法。本文采用碰撞仿真软件PAM-CRASH进行计算。该软件应用于汽车、铁路车辆和航空航天等领域内的碰撞研究工作中，其完善的碰撞模拟方案受到广泛认可。

2.2 耐撞性计算模型

结合某地铁车辆头车结构，建立前端司机室有限元模型。以四节点壳单元为主，三节点三角形单元为辅划分模型。其单元总数为23 466，节点总数为27 087。该司机室为对称结构，将对耐撞性能可能产生影响的结构板厚作为变量，位置标示见图1。

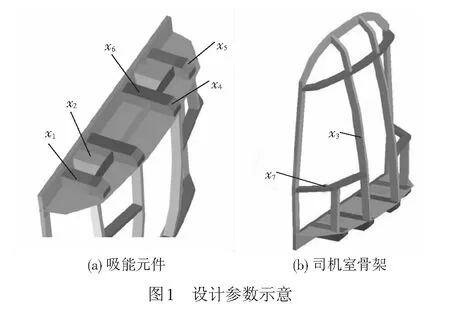
结合设计经验，设定各厚度参数下限为2 mm，上限为8 mm。参照BS EN 15227:2008标准[16]，同时考虑减少单元数量，提高计算效率，在司机室后端按照编组质量进行集中配重,整体以25 km/h的速度撞击静止刚性墙。

碰撞过程中，结构的总能量变化和接触力变化见图2。

总吸能量和接触力峰值是评价结构耐撞吸能的重要指标，因此分别以这两个指标作为目标响应，借助Matlab软件中的Dace工具箱构建Kriging模型，选择二次回归函数，高斯相关方程。

为检验Kriging模型的准确性，共选取了30个随机点计算其误差，模型拟合精度检验见表2。其中以总吸能量为目标函数时的最高误差为2.07%，平均误差为0.72%；以接触力峰值为目标函数时的最高误差为1.92%，平均误差为1.43%。

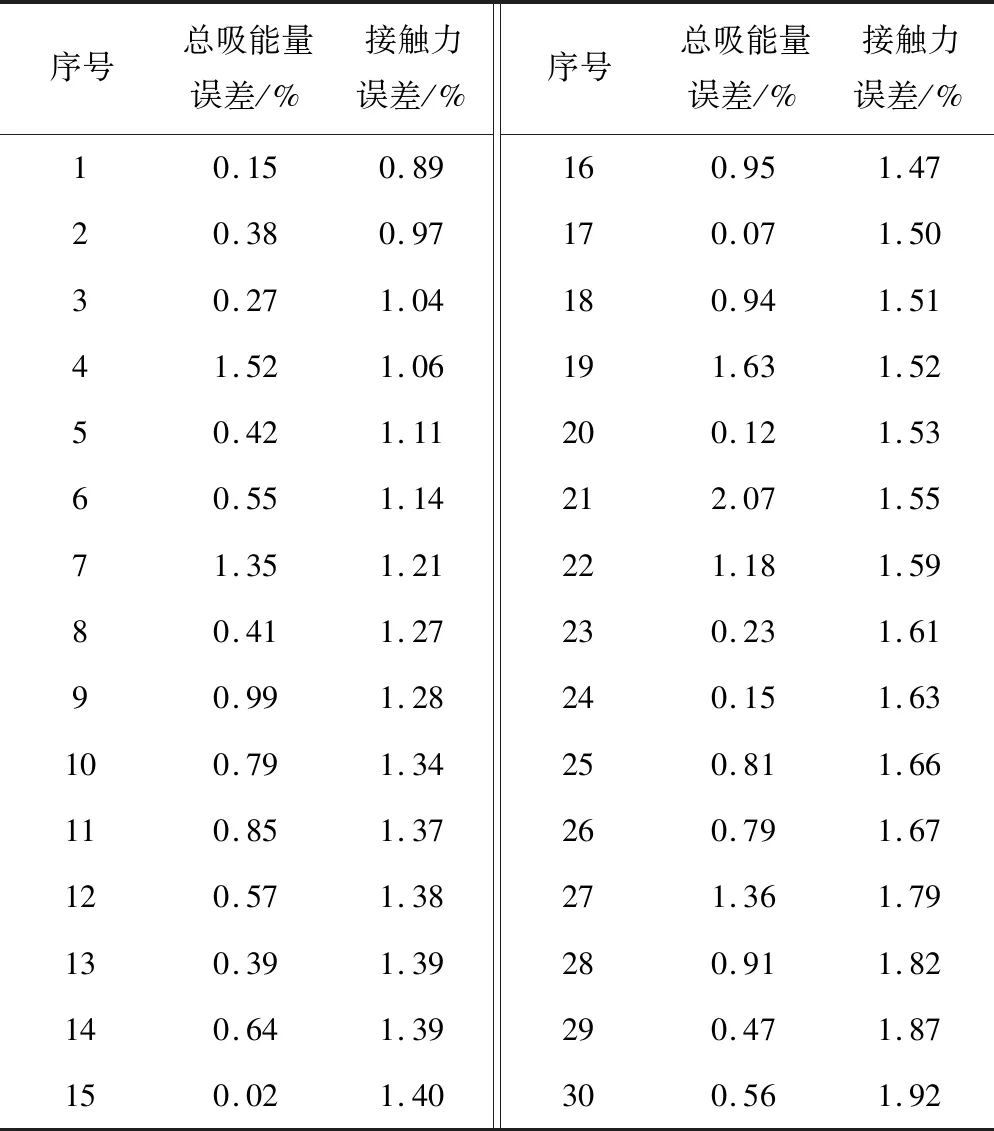
表2 Kriging模型拟合精度检验

误差在可接受范围内，模型精度满足要求，可继续进行Sobol’灵敏度分析。

2.3 总吸能量为目标响应的灵敏度分析

主灵敏度表示的是单个参数变化对输出结果的影响，而总灵敏度还反映了与其他参数交互作用共同产生的影响。以总吸能能量为目标时，各输入参数的主灵敏度和总灵敏度见图3。

由图3可见，设计参数x1，x2，x3的灵敏度值较大，对结构总吸能量有较大影响。同时注意到参数x2,x3,x6的主灵敏度与总灵敏度相差较大，说明该参数与其他参数交互效应对输出参数产生了较大影响，因此针对各参数间的交互效应进一步分析，得到图4所示二阶交互效应热图。

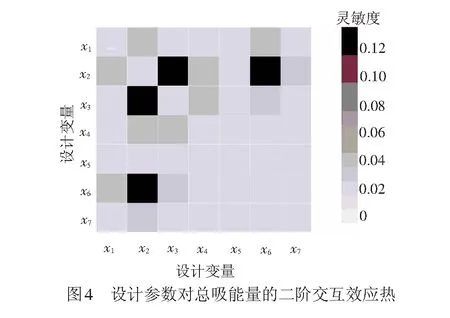
由图4可见，参数x2与x3、x2与x6的交叉处色块颜色较深，灵敏度较高，因此在结构优化中，在对总灵敏度较大的参数重点优化时，应同时注重这两对参数间的合理搭配，以达到更优的结果。

2.4 接触力峰值为目标响应的灵敏度分析

同理，将接触力峰值设为目标响应，得到的一阶主灵敏度和总灵敏度值见图5。

设计参数x1，x2的灵敏度值较大，对接触力峰值有较大影响。同时注意到各参数的主灵敏度和总灵敏度相差较小，因此可推断交互效应所产生的影响会很小。各参数二阶交互效应热图也验证了这一预测，见图6。

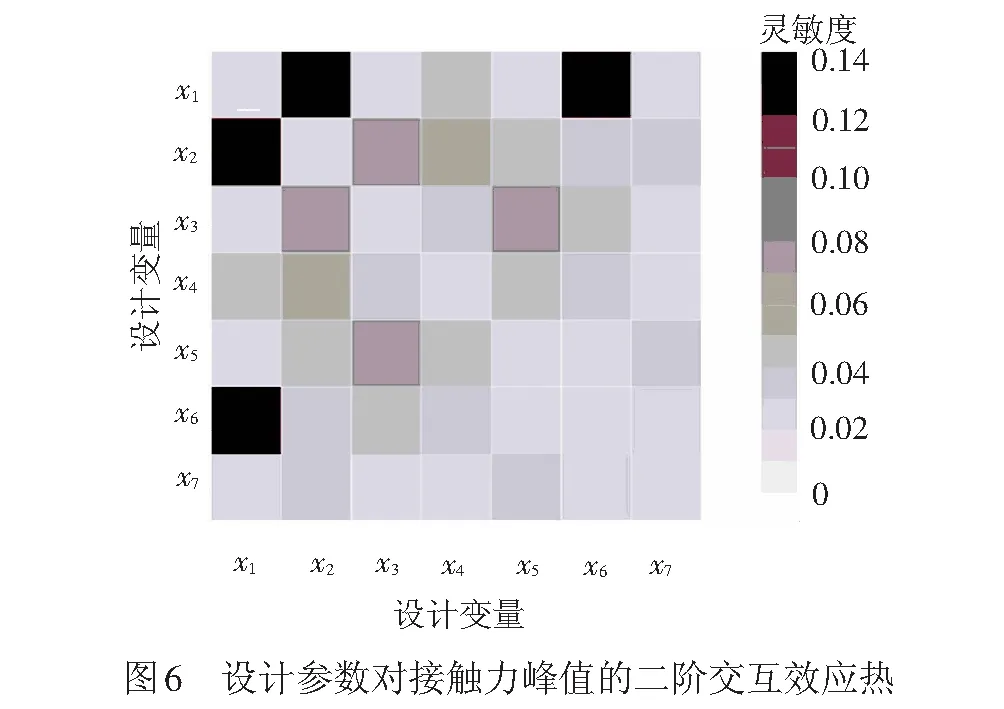
由图6可看出，参数间二阶交互效应均较小，因此在优化中可合理忽略参数间的搭配组合，着重对主灵敏度较大的x1、x2参数进行优化。

3 优化结果对比

根据灵敏度分析结果，将原模型的7个设计参数简化为仅包含灵敏度较高的4个参数的简化模型，利用ISIGHT软件，分别对原模型和简化后的模型进行尺寸优化，优化结果见表3。

表3 原模型与简化模型优化结果对比

灵敏度分析辨别了设计参数中较为敏感的参数，简化模型进行优化，迭代步数减少46%，极大降低了优化工作量。得到的优化结果与考虑所有设计参数的优化结果相比，总吸能量仅减少了1.5%，而接触力峰值则相应降低了70 kN，差异极小且各有优劣。此结果反映了Sobol’灵敏度方法在轨道车辆吸能结构优化设计过程中的可行性和实用性，不仅能较大程度上减少实验成本和计算耗时，且能得到极好的优化结果，具有现实指导意义。

4 结论

本文使用Sobol’方法，通过构建Kriging代理模型计算了轨道车辆前端吸能结构的全局灵敏度，并将基于灵敏度分析简化模型后的优化结果与原模型优化结果进行了对比，研究结果表明：

(1) Sobol’全局灵敏度法能处理大型复杂非线性问题，并可分析各参数间交互效应对结果的影响。

(2) 构建Kriging代理模型计算Sobol’灵敏度仅基于已有样本，同时具有较高精度。

(3) 通过对某地铁前端吸能结构的全局灵敏度分析，可找出较为敏感的参数，对结构优化提供有力参考。