内膛损伤枪管膛口扰动参数研究

2020-04-16沈超周克栋赫雷陆野李峻松

兵工学报 2020年3期

沈超，周克栋，赫雷，陆野，李峻松

(1.南京理工大学机械工程学院，江苏南京 210094；2.中国兵器工业第208研究所，北京 102202)

0 引言

理想状态下，弹头沿枪管内膛的运动可以分解为弹头沿枪管轴向的直线运动和绕枪管轴线的旋转运动，弹头几何轴线方向(弹头尾部指向头部)、弹头回转角速度方向(右旋弹)及弹头平动速度向量均保持同向，并且弹头直线运动速度、旋转角速度以及膛线缠度之间满足确定的数学关系，即无量纲转速ω*=ωD/vm(ω为弹头自转角速度，D为弹头圆柱部直径，vm为质心速度)由膛线缠度决定。实际射击过程中，由于弹头嵌入膛线前其空间位置不完全确定、弹头外形及膛线尺寸不完全对称等各种不可控因素的影响，弹头挤进及沿内膛向枪口运动过程中，弹头质心会在垂直枪管轴线平面内产生波动，产生非轴向质心速度；弹头除绕自身几何轴线自转运动外，还存在其自转轴线的进动和章动现象，从而导致弹头速度方向、自转角速度方向和几何轴线方向之间产生一定的夹角，弹头无量纲转速也会产生波动。初始摆动角、初始攻角、初始偏角以及初始无量纲转速改变量等构成了弹头出膛时的初始扰动状态，简称为弹头膛口扰动状态。弹头膛口扰动是影响射击精度的重要因素，研究枪管内膛有损伤时枪管或弹头随机因素对弹头膛口扰动的影响，是更深入理解内膛损伤导致精度下降、椭圆弹孔率增加等机理的关键。

国内外学者对枪管或弹头随机因素对弹头膛口扰动和射击精度的影响进行了系统研究。芮筱亭等[1]和芮筱亭[2]建立了弹丸发射动力学模型，采用传递矩阵法等方法研究了弹丸发射过程中弹炮系统的运动规律，阐述了各类弹炮系统弹丸起始扰动的形成原因。张治彬等[3]基于Monte Carlo方法，以射击准确度、密集度、命中概率等作为评价指标，对轻气炮射击精度进行了评估。王丽群等[4]基于随机模型和随机优化的稳健设计理论，提出了以射击密集度为指标要求的随机因素参数区间计算方法，对炮或弹随机因素进行了优化设计。Zelenko等[5]研究了枪管内膛磨损与枪弹结构的关系，并获得了由铜质弹头壳和铅芯组成的软质弹头磨损特征与机理。上述研究均未考虑真实枪管内膛损伤(包括裂纹、烧蚀坑、铬层剥落及磨损等)对内弹道过程及弹头出膛状态的影响，无法对枪管射弹量增加后的精度下降、横弹孔率上升等作出很好的解释。

研究枪管或弹头随机因素影响下的弹头膛口扰动随机响应常采用的方法有Monte Carlo方法、随机动力学方法和代理模型法等，代理模型法又包括响应面法(RSM)、径向基函数及人工神经网络等，其中RSM由于原理简单且易于实现获得广泛关注。RSM实施过程中需要解决3个关键问题，即试验设计、选取响应面函数、模型拟合。试验设计方面，吕大刚等[6]从求解精度和计算效率两方面比较了均匀设计RSM和Monte Carlo等方法在预测钢框架结构抗震可靠度问题上的有效性，结果表明，均匀设计RSM可以在更好地拟合结构功能函数曲面的前提下显著减少试验次数，节约时间成本。胡常福等[7]提出均匀设计RSM和牛顿迭代法相结合的索拱桥索力优化方法，可以明显减少试验次数和优化迭代次数。

传统的均匀设计RSM需要预先假定特定形式的响应面函数，然而在实际工程问题中，响应面函数形式往往不能预知其具体形式，事先假定模型的形式会限制该方法的计算精度[8]。尽管均匀设计方法可以显著减小试验样本数，但一方面小样本数据间往往会存在变量的多重相关性；另一方面，为解决变量间函数形式未知的非线性问题，建模方法通常是将非线性转化为拟线性，通过对初始变量进行适当变换，将初始变量间的非线性关系变为拟线性关系，再使用线性理论进行响应面方程的求解，这一过程往往会使变量维数增加，且变换后的变量间极有可能产生多重相关性[9]。基于上述两方面原因产生的变量间多重相关性，若仍采用传统最小二乘法拟合响应面函数，则其准确性和可靠性都难以保证。

本文在系统的枪管寿命试验获得某12.7 mm机枪枪管内膛损伤不同寿命阶段主要形式及分布规律的基础上，采用均匀设计方法安排了弹药随机因素影响下的损伤枪管内弹道过程仿真实验。利用有限元方法对损伤枪管的内弹道过程进行了建模及仿真计算并获得了弹头的膛口扰动随机响应值，采用基于样条曲线的偏最小二乘回归建模方法获得了膛口扰动的响应面方程。研究了枪管不同损伤程度下弹药随机因素对弹头出膛时初始扰动状态的影响规律，获得了影响各寿命阶段枪管弹头膛口扰动的主要因素，并针对延长枪管寿命提出了弹药参数的优化方向。

1 损伤枪管枪弹相互作用有限元模型

为研究枪管寿终机理，获得枪管内膛损伤的主要形式及分布规律，在相同射击规范下，对多根相同结构、相同材料及相同内膛表面镀层工艺的某12.7 mm机枪枪管进行了系统的寿命试验。在各根枪管的各寿命阶段，使用塞规测量其内膛各处的直径变化情况，并使用内窥设备记录其内膛表面形貌状态。通过对多支枪管的内膛损伤数据进行分析可以发现，各根枪管在相同寿命阶段时，其内膛直径尺寸沿枪管轴向的变化情况、内膛的损伤形式及损伤的分布规律表现出很大的一致性，并且枪管内膛直径及表面形貌随射弹量增加的变化情况表现出较强的规律性，为建立弹头沿各寿命阶段损伤枪管运动的内弹道过程有限元模型提供了依据。

寿命试验结果表明，枪管内膛损伤的主要形式有内膛表面的磨损、裂纹、烧蚀坑及镀层的剥落等，如图1所示(内窥视频截图，位于坡膛与线膛交界处)。由图1可见，内膛表面磨损会使枪管内径增大，降低内膛对弹头的导向及导转作用，使弹头在内弹道过程中的扰动增大、导转力减小、转速降低；裂纹、烧蚀坑等会增大弹头挤进及沿膛运动的不稳定性，影响弹头嵌入膛线过程及沿线膛运动过程中弹头壳的表面形貌状态，导致弹头气动性能发生改变，影响其外弹道性能。在上述因素综合影响下，随着射弹量的增加，弹头出膛口时初始扰动量及气动性能均与无损伤枪管发射的弹头有较大差异，从而导致散布圆半径和椭圆弹孔率的增加，使枪管寿终。

图1 内膛损伤形式Fig.1 Damage forms of bore

为便于建立损伤枪管的有限元模型，将枪管内膛的损伤形式分为2类：第1类为内膛沿径向的均匀磨损，枪管同一截面周向各处磨损量相同，各寿命阶段枪管内膛轴向各处的磨损量由塞规测量得到；第2类为改变内膛表面形貌状态的裂纹、烧蚀坑及铬层剥落等，各寿命阶段枪管内膛的表面形貌状态由内窥视频获得。建立真实的损伤枪管有限元模型时，必须同时考虑上述2种内膛损伤形式。

综合上述分析，本文提出损伤枪管有限元模型的建模方法为：首先使用三维建模软件(如UG、SolidWorks等)建立只含第1类损伤的枪管三维模型，然后采用Hypermesh软件对其进行有限元网格划分；在此基础上，基于寿命试验获得的枪管各寿命阶段第2类损伤的分布规律，在内膛轴向相应损伤处预置裂纹、烧蚀坑等损伤。采用这种方法即可建立不同寿命阶段损伤枪管的有限元模型。

寿命试验所得枪管内膛损伤数据的分析及损伤形式和分布规律总结过程、各种形式内膛损伤建模方法、内膛损伤枪管有限元模型建立过程、弹头壳材料本构模型及弹头沿不同寿命阶段枪管内膛运动的内弹道计算模型建立过程详见参考文献[10]。

2 非线性偏最小二乘回归法

2.1 均匀设计方法

均匀设计是由我国数学家王元和方开泰于20世纪70年代末提出的一种试验设计方法[11]，属于伪Monte Carlo法的范畴，与正交设计、中心复合设计法等相比，正交设计法在因素水平数较多时可以显著降低试验次数、节约时间和经济成本。可以证明[11]：正交设计法与均匀设计法在保证相同均匀性的前提下，二者所需的试验次数量级分别为O(q2)与O(q)(q为因素水平数)，可见均匀设计法能在较好地反映试验体系主要特征前提下大大减少试验次数，且相对于正交设计法不会产生大的偏差，因此本文选择均匀设计方法设计弹药随机因素影响下损伤枪管内弹道过程的仿真实验过程。

2.2 偏最小二乘回归法

偏最小二乘方法是在主成分分析和典型成分分析的基础上建立起来的，其核心思想是为了避免自变量之间多重相关性导致的较大舍入误差。因此可以不再考虑直接建立自变量与因变量间的回归模型，改为对变量系统中的数据进行重新综合筛选出新的变量，筛选标准为新的变量应尽可能多地携带其数据表中的变异信息。基于新提取的变量进行回归建模，可以克服变量间的多重相关性造成的信息重叠，从而提高回归模型的准确性。偏最小二乘回归法的实施步骤如下：

步骤1对自变量矩阵Xn×p和任一因变量y分别做标准化处理，处理后分别对应标准化矩阵E0=(E01,E02,…,E0p)n×p和矩阵F0，其中n为样本点数(即实验次数)，p为自变量数或因素数。标准化处理是为了消除变量的量纲效应，使每一个变量都具有同等表现力，并使变量数据呈中心化分布，处理方法如(1)式所示：

(1)

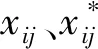
步骤2基于交叉有效性原则，从自变量矩阵E0中提取m个(m≤r(X)，r(X)为自变量矩阵的秩)主成分向量t1,t2,…,tm，且t1,t2,…,tm均可以表示为E01,E02,…,E0p的线性组合，并求得F0在t1,t2,…,tm上的普通最小二乘回归方程为

F0=r1t1+r2t2+…+rmtm+Fm，

(2)

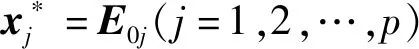
(3)

式中：α1、α2、…、αp为原标准化自变量的回归系数。去除(3)式中的残差项，即可得到最终的响应面方程为

(4)

2.3 基于样条变换的偏最小二乘回归法

传统的均匀设计RSM需要预先假定特定形式的响应面函数，然而在实际工作中，人们通常只能获得自变量与因变量的观测数据合集，无法获知其具体的模型关系形式，尤其是在自变量维数较高且自变量与因变量之间是非线性关系时。此时可以采用一种各维变量的加法模型[8]：

y=f1(x1)+f2(x2)+…+fp(xp)+ε，

(5)

式中：ε为残差。

可以根据拟线性思想，将(5)式中的自变量函数fj(xj)进行变量替换、消除非线性成分，以得到一个拟线性回归模型，使模型求解过程可以得到明显简化。但是实际问题中fj(xj)往往是未知的，无法求解模型，此时可以采用数值分析理论中的样条函数对自变量函数fj(xj)进行逼近，即选取一个样条函数φj(xj)，使得φj(xj)≈fj(xj)，从而(5)式中的加法模型可以通过样条函数进行转换得到：

y=φ1(x1)+φ2(x2)+…+φp(xp)+ε.

(6)

实际工程中应用最广的样条曲线为3次B样条拟合函数[12]，其展开形式为

(7)

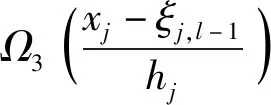
(8)

(9)

在计算过程中，自变量xj上的最小观测值记为minxj、最大观测值记为maxxj，则有

ξj,l-1=minxj+(l-1)hj，l=0，1，…，Mj+2，

(10)

式中：

(11)

将(7)式代入(6)式，可以得到自变量与因变量的非线性响应面函数关系为

(12)

2.4 弹头膛口扰动参数响应面模型建模方法

将基于样条变换的非线性偏最小二乘回归建模方法与传统均匀设计RSM相结合，以确定损伤枪管所发射弹头在弹药随机因素影响下的膛口扰动状态。具体步骤如下：

1)根据设计指标及样本测量值确定弹药随机参数的取值范围，即自变量x的取值空间。

2)在抽样空间内进行均匀设计，根据自变量数目及拟进行的实验次数选择偏差较小的均匀设计表。

3)在每个弹药随机参数的样本点处采用枪弹相互作用有限元模型，计算得到弹头膛口扰动的参数值。

4)对自变量空间X=[x1x2…xp]的每一维xj(j=1,2,…,p)做3次B样条变化xj→Zj：∀j=1,2,…，p,确定变量区间的分段数Mj、分段长hj及分段点ξj,l-1；对xj做3次B样条变换，即

(13)

记Zj=[zj,0,zj,1,…,zj,Mj+2]。

5)对因变量及新的自变量进行标准化处理，并应用(2)式～(4)式求得因变量关于新自变量的回归系数βj,l(j=1,2,…,p;l=0,1,…,Mj+2) ，即

(14)

6)将回归系数βj,l和3次B样条变化(13)式代入(14)式，即可得到y关于初始自变量X的非线性回归模型。

以上给出了根据原始数据表(X,y)建立整体非线性模型的方法。

3 模型验证及结果分析

3.1 弹药随机参数的选择

某型号12.7 mm重机枪固定于固定枪架上进行射击时，枪械本身的随机因素对弹头膛口扰动的影响较小。不同寿命阶段的枪管，影响其弹头膛口扰动的主要因素为弹药参数的随机误差，其中主要因素有弹头形状及质量等制造误差、发射药质量及药形等误差、弹头与内膛间隙及起动压力的随机性等。

由于影响弹头膛口扰动的因素太多，全面分析各因素对膛口扰动的影响是不实际的，工程实践中往往更关注若干主要因素对膛口扰动量的影响。依据相关的理论和实践经验，本文选取以下5个弹药参数作为主要影响因素：弹头圆柱部直径、弹头质量偏心、弹头质量、弹头壳材料常温屈服强度及装药量。

3.2 弹药随机参数均匀设计表

5个弹药参数分别取11个水平值，取值范围及均匀设计步长如表1所示。均匀设计表通常用符号Un(qp)表示[13]，其中U表示均匀设计，n、q、p如前文所述分别为试验次数、各因素水平数和因素数。本文采用的均匀设计表为U11(1110)，该均匀设计表最多可以安排6个因素数的试验，按照相应的使用表，本文的5因素11水平值试验选取U11(1110)表的第1、2、3、5、7列进行试验设计，最终弹药随机因素的均匀设计仿真实验安排如表2所示。各弹药参数间的相关系数如表3所示，可以看出变量间存在较强的多重相关性。

表1 弹药参数取值范围及均匀设计步长Tab.1 Value range of ammunition parameters and steps for uniform design

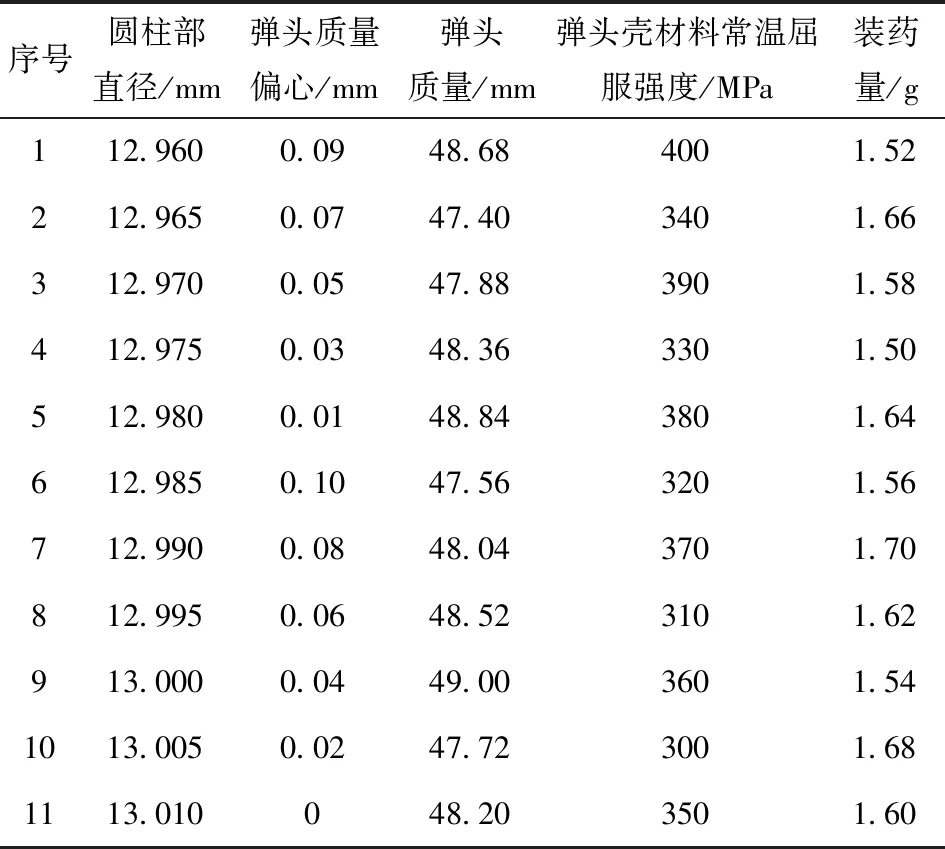
表2 均匀设计取值表Tab.2 Value table of uniform design for ammunition parameters

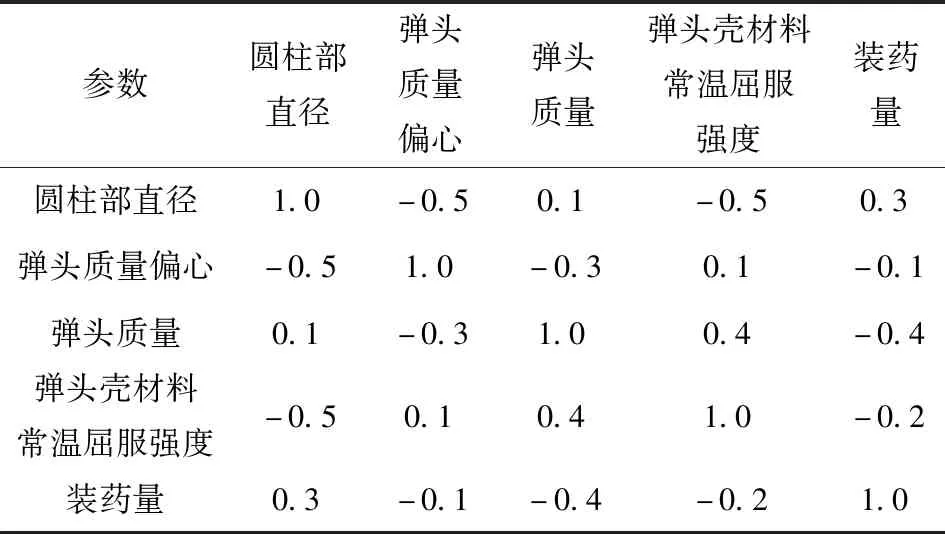
表3 弹药参数间的相关系数Tab.3 Correlation coefficient between ammunition parameters

3.3 模型验证

进行枪管寿命试验时，枪管寿终的判定标准[14]为：弹头出膛速度下降率超过15%；100 m靶处椭圆弹孔(长轴与短轴比大于1.25)率超过射弹数的50%；3次100 m靶散布密集度平均值R50≥30 cm.寿命试验中，该12.7 mm机枪的散布圆半径和椭圆弹孔率会随射弹量的增加发生显著改变，弹头出膛速度则基本不变。

针对某12.7 mm机枪枪管，依照上文所述方法分别建立射弹量为0发、1 400发、3 000发及6 000发枪管的弹枪热力耦合模型，对应于枪管的4个寿命阶段，即无损伤枪管、寿命中前期枪管、寿命中期枪管和寿终枪管，并将所建立的4个寿命阶段枪管有限元模型按射弹量由低到高分别编号为1～4号。依照表2中的弹药随机因素取值，对这4个寿命阶段枪管分别进行11次内弹道过程仿真实验，并在弹头质心和地面坐标系之间建立无约束的连接器，获得共44组弹头膛口扰动参数响应值，弹头膛口扰动参数主要包括初始摆动角、初始攻角、初始偏角以及初始无量纲转速。

根据仿真实验获得的4个寿命阶段枪管所发射弹头的膛口扰动数据，结合弹头6自由度刚体外弹道方程，编程求解其外弹道过程，获得了4个阶段枪管所发射各11发弹头在100 m处的散布圆半径R50和椭圆弹孔率情况，并将其与寿命试验数据进行了对比，结果如表4所示。由表4可以看出，由仿真实验获得的弹头膛口扰动状态参数计算得到的100 m处散布圆半径和椭圆弹孔率均与试验结果吻合得很好，验证了本文所建立枪与弹相互作用有限元模型的准确性，以及用仿真方法获得的弹头膛口扰动数据研究弹药随机因素对膛口扰动影响规律的合理性。

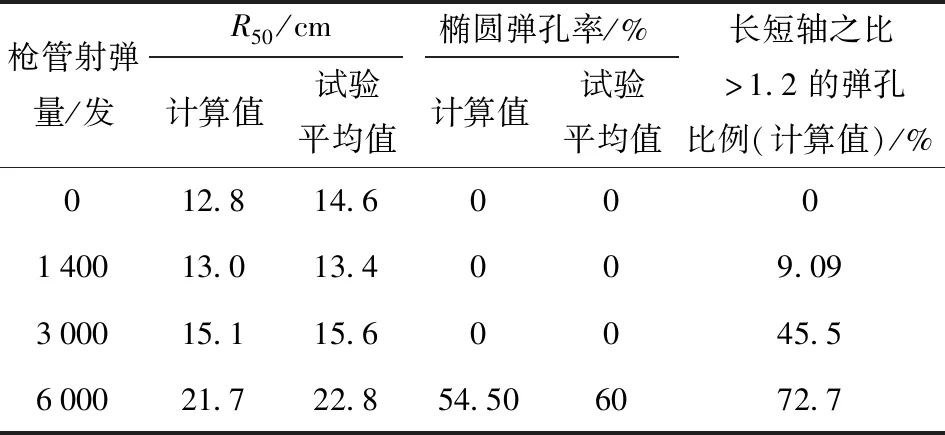
表4 100 m靶散布密集度及椭圆弹孔率Tab.4 Dispersion circle radius and elliptical shot hole ratio at 100 m

此外，由表4还可以发现，尽管12.7 mm机枪枪管是在最后一个寿命阶段后椭圆弹孔率突然增加而导致其寿终，但其实在这之前早在寿命中期阶段时，长短轴之比大于1.2的弹孔数量就已明显增加至接近精度测试射弹量的50%，只是还没有增大到1.25这一阈值而已，而在枪管寿终时，长短轴之比大于1.2的弹孔数已达到8个，占一共11发射弹的72.7%.

3.4 结果分析

3.4.1 仿真实验结果分析

仿真实验获得的4个寿命阶段枪管所发射弹头膛口初始攻角、初始偏角、初始摆动角，以及初始无量纲转速随弹药参数变化的响应值均值和标准差分别如表5和表6及图2和图3所示。由表5和表6及图2和图3可以看出，随着射弹量的增加，除初始无量纲转速外的膛口扰动参数均值及标准差都在增加，即内膛损伤越严重的枪管，其发射的弹头膛口扰动值、膛口扰动状态的波动范围就越大，无量纲转速也越低。此外，还可以发现在枪管寿命的中前期，各膛口扰动参数值较初始状态的改变量较小；而在寿命末期，各膛口扰动参数值迅速与初始状态产生较大偏差，这与枪管寿命试验及外弹道仿真计算中散布圆半径R50和椭圆弹孔率随射弹量增加的变化情况是一致的，可见由内膛损伤引起的弹头膛口扰动状态的改变是导致枪管寿终的主要原因。

表5 膛口扰动均值Tab.5 Mean values of muzzle disturbances

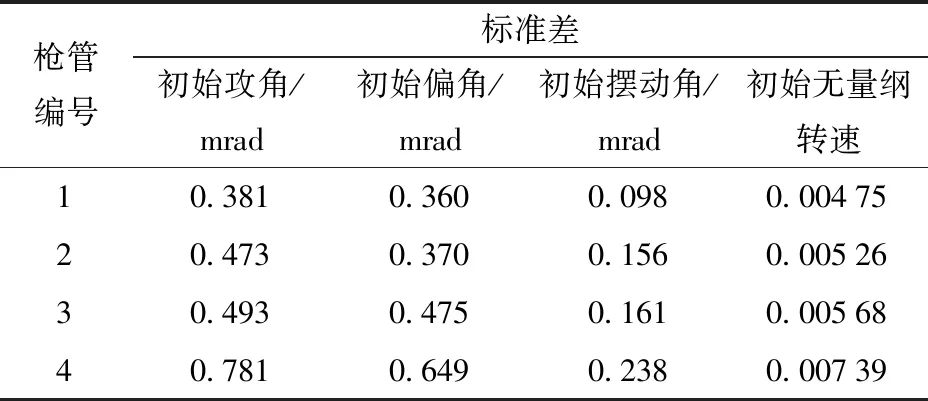
表6 膛口扰动标准差Tab.6 Standard deviations of muzzle disturbances

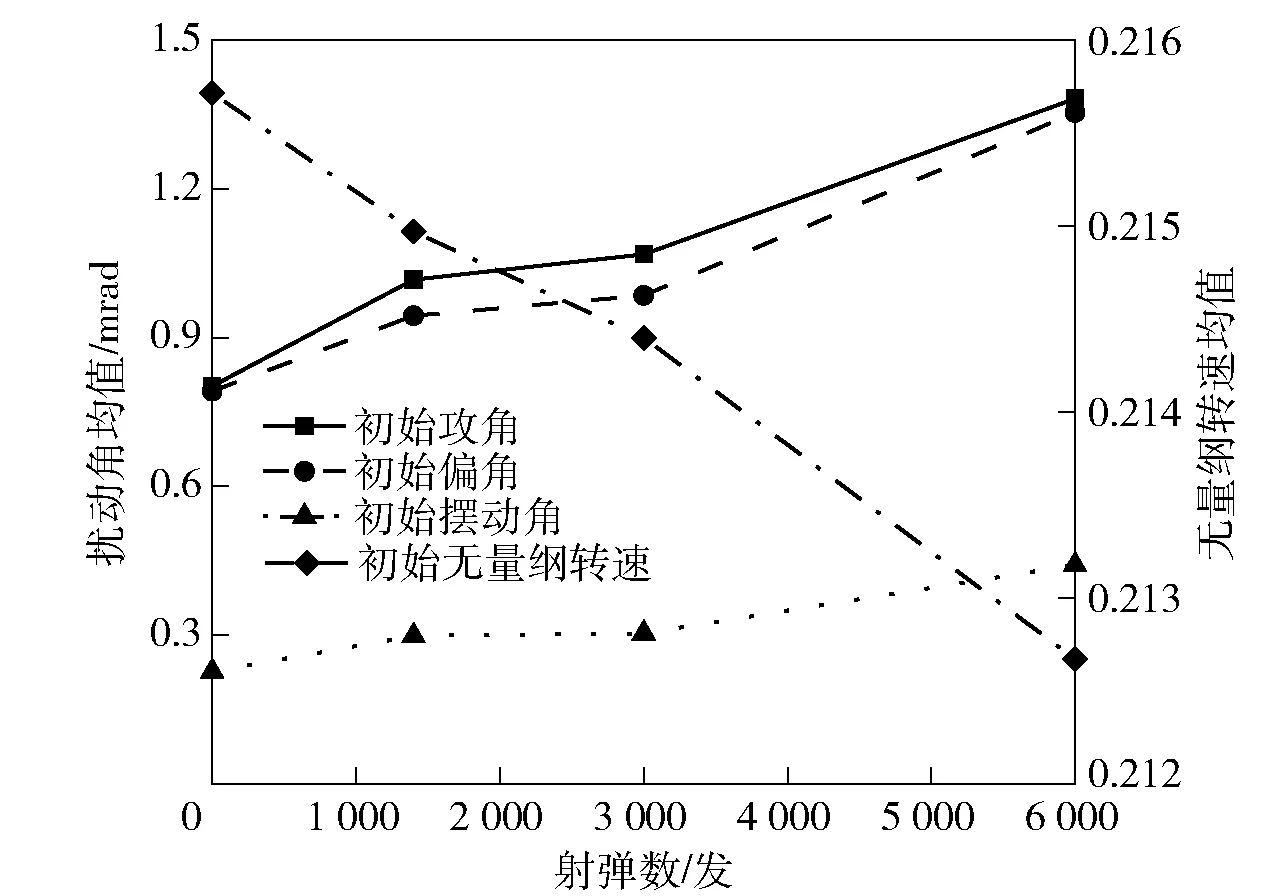
图2 膛口扰动均值随射弹数变化趋势Fig.2 Mean values of muzzle disturbances versus fired rounds

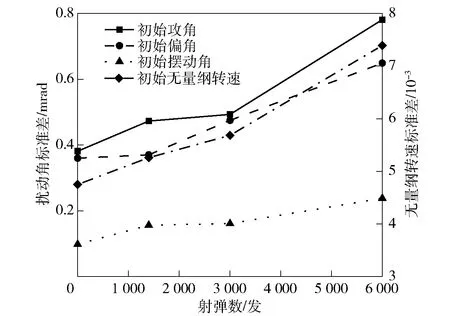
图3 膛口扰动标准差随射弹数变化趋势Fig.3 Standard deviations of muzzle disturbances versus fired rounds

3.4.2 回归分析

由于均匀设计法不具有正交设计法的整齐可比性，要研究各弹药因素对弹头膛口扰动状态的影响程度差异，还需要对仿真实验结果进行回归分析。本文分别采用传统二次拟线性回归模型和基于样条变换的偏最小二乘回归模型对仿真实验结果进行回归分析，同时针对可能出现的某个弹药因素对某些膛口扰动参数有显著影响，而又对其他膛口扰动参数没有显著影响的现象，导致难以综合评价其对膛口扰动影响大小的现象，基于吴宏[15]提出的起始扰动综合量概念，将上述4个主要的膛口扰动参数均纳入其中，建立了新的膛口扰动综合量参数Rd，以综合考虑上述各因素对膛口扰动的影响，其表达式如(15)式所示：

(15)

式中：ny为因变量数；yj为因变量向量；minyj表示取yj向量中的最小值，这里取最小值而不取均值，可以避免正值与负值的相互抵消；σj为yj的标准差。由(15)式可以看出，Rd综合考虑了膛口各扰动参数，任一膛口扰动值的增加均会引起Rd的增加，因此可以用Rd来表征膛口扰动的大小。

分别采用拟线性回归方法和基于3次B样条曲线的偏最小二乘方法，对膛口扰动参数进行拟合，获得其响应面方程。为比较两种回归模型的精度，以膛口扰动综合量Rd为例，以无损伤枪管的仿真实验值Rd为横坐标、拟合值d为纵坐标，两种方法的拟合效果及相对误差分别如图4和图5所示。

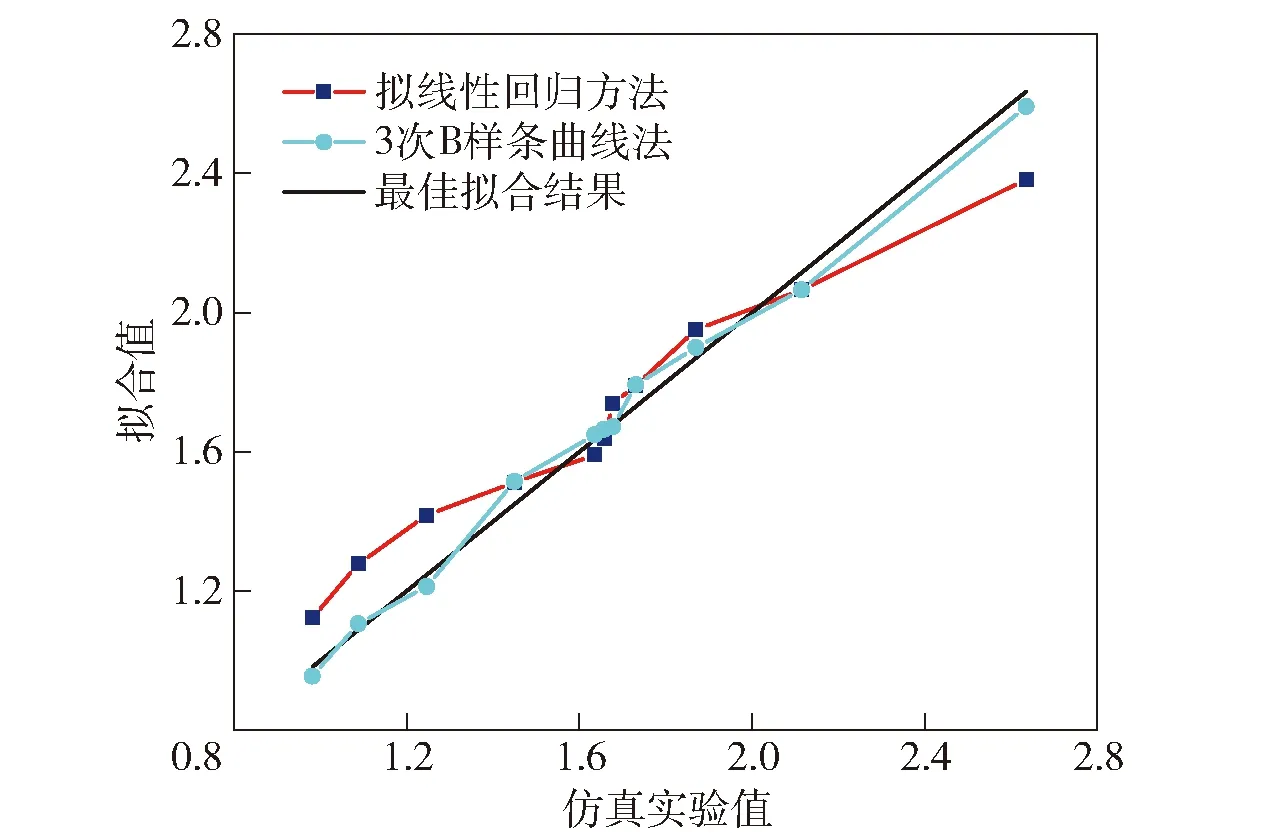
图4 无损伤枪管Rd拟合效果图Fig.4 Fitting effect of Rd of undamaged barrel

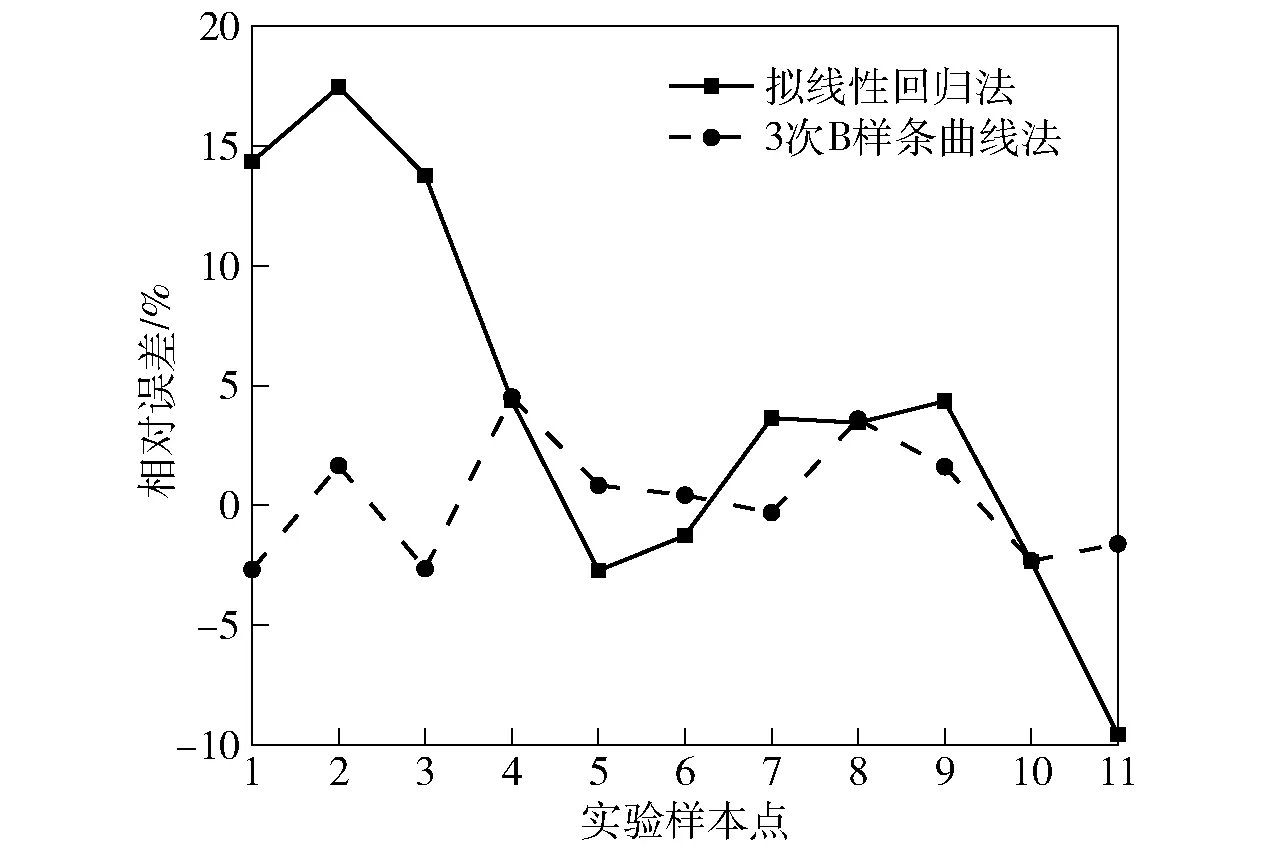
图5 无损伤枪管Rd拟合值的相对误差Fig.5 Relative error of fitting values of Rd of undamaged barrel

从图4和图5中可以看出，基于样条曲线的偏最小二乘方法拟合值较拟线性回归法明显更接近最佳拟合结果，2种方法所得Rd响应面函数的拟合系数R2为0.992和0.922(R2越接近1，表示拟合度越高)，可见采用基于样条曲线的偏最小二乘方法可以较显著地提高响应面方程的准确度。为了验证基于样条曲线的偏最小二乘方法在提高拟合度的同时没有出现过拟合现象，又随机安排了3组仿真实验，实验所取弹药参数值从表1内随机重新组合获得，并将其代入拟合好的响应面方程内，所得膛口扰动综合量的估计值d与仿真实验值的相对误差均在10%以内，没有出现过拟合现象。

基于样条曲线的偏最小二乘方法，可以实现将5个弹药因素对各膛口扰动参数的贡献值分开，单独考虑各因素对膛口扰动量的贡献效果。以膛口扰动综合量Rd为例，弹头圆柱部直径、弹头质量偏心、弹头质量、弹头壳材料常温屈服强度及装药量共5个弹药因素对4个寿命阶段枪管所发射弹头的Rd贡献度分别如图6(a)～图6(e)所示。

由图6可以看出，不同寿命阶段的枪管，各弹药参数对膛口扰动综合量的贡献度均不相同、膛口扰动量相对于各自变量的单调性及敏感程度也不同。对于无损伤枪管，膛口扰动综合量受弹头圆柱部直径及弹头质量的影响较大，在弹头圆柱部直径较小、弹头质量在均值左右时，其发射弹头的膛口扰动综合量较低，这是因为无损伤枪管由于其内膛没有磨损等损伤，内膛阴线、阳线直径较小，过大的弹头圆柱部直径会导致弹头挤进及沿膛运动过程中变形量及受力增大，更容易放大由其他因素引起的扰动量。对于寿终枪管，可以从图6中明显看出其发射弹头的膛口扰动综合量受各因素的影响均明显增大，较小的弹药因素波动就可能导致较大的弹头膛口扰动状态改变，其中弹头圆柱部直径、弹头质量偏心及弹头壳初始屈服应力对膛口扰动状态的影响尤为明显。这是因为寿终枪管的内膛磨损量最大，铬层剥落现象严重，弹头内弹道过程中所受导向及导转作用均明显降低，初始弹药条件的细微改变就会导致弹头出膛时攻角、转速等较大波动，其中弹头圆柱部直径直接影响弹头与枪管内膛间的过盈量，以及枪管对弹头的导转及导向作用；弹头质量偏心在枪管对弹头的导向作用降低时会明显增加弹头质心在垂直枪管轴线截面内的波动范围，增大弹头姿态的不确定性；弹头壳初始屈服应力主要影响弹头的挤进过程，由寿命试验可以发现，寿终枪管的坡膛段损伤最严重，初始屈服应力改变会使弹头挤进完成时的扰动量产生较大波动，增大内弹道起始阶段弹头姿态的不确定性。此外还可以发现，装药量对无损伤枪管和寿终枪管的膛口扰动综合量影响均较小，装药量适中时对应最小的膛口扰动综合量。

综上所述，通过分析寿终枪管所发射弹头膛口扰动参数随弹药因素的变化规律，为提高枪管寿命，应尽量减少弹头的质量偏心，在表1给出的范围内适当减少弹头壳初始屈服应力并取适中的弹头壳圆柱部直径和装药量。