双车厢两栖车静水直航下的水动力性能研究

王少新，金国庆，王涵，孙蕊，刘贺

(1.大连理工大学 船舶工程学院，辽宁 大连 116024；2.大连驭海佳艺咨询科技有限公司,辽宁 大连 116000；3.哈尔滨第一机械集团有限公司，黑龙江 哈尔滨 150056)

0 引言

水陆两栖车依靠车轮或履带实现陆地上行走，依靠推进式螺旋桨或喷水推进装置实现水上航行，无论在国防还是民生经济领域都有较大的市场需求，如军事上可作为突击登陆、巡逻运输和资源补给等；在民用上可用于抗洪救灾、运送人员和物资等[1-2]。两栖车在陆地上的行进过程与普通车辆无异，但在水中航行时受水动力环境影响较大，如存在对航行速度的要求，由于两栖车属于钝体结构物，流线型较差，导致水阻力大，此时必须考虑车辆外形设计以减小水阻力，以及采用高效的推进设备实现航速要求。此外，海洋环境的恶劣对两栖车辆的稳性和耐波性提出了更高要求[3]。近年来，为提高两栖车的运载能力，有关单位研究开发了某型号双车厢水陆两栖车，车身长18.5 m，最宽处宽度5.2 m，设计吃水线距离轮毂中心线1.472 m，在静水正浮状态下横倾角和纵倾角均为0°；满载排水量约为88 t，前车厢排水量38 t，主要布置车用行进设备和驾驶人员，后车厢排水量50 t，主要用于存放运载货物与人员；前后两车厢中间采用铰接形式连接，铰接设备安装在水密箱体内部；前后车厢各布置两个推进装置，用以克服双车厢存在的水阻力；对于两栖车，为防止出现大幅度埋首现象(该现象通常会导致两栖车在水中纵倾角太大而倾覆)，防浪板[4]的设计安装必不可少。本文研究的两栖车模型选用具有一定厚度的方形板作为防浪板，安装角度为35°.双车厢的设计可大幅改善两栖车辆的运输能力，本文研究的两栖车计算简化模型主视图和俯视图如图1所示。基于该背景，本文主要基于数值方法对双车厢两栖车的水动力性能进行仿真研究，以服务于工程设计。

图1 双车厢两栖车计算简化模型Fig.1 Simplified model of a double-carriage amphibious vehicle

对于两栖车水中阻力与运动性能的测量，传统做法是基于相似理论，采用缩尺模型进行拖曳水池试验[5]，该试验方法的可靠性较高，但是试验成本较高、周期较长，大量的工况无法全部通过试验完成。近年来，随着计算流体力学(CFD)的发展，船舶运动与水动力性能计算的精度大幅提高，此外，计算机处理数据性能的提升也进一步推动了CFD方法在船舶工程中的实际应用。李玉良等[6]采用CFD多相流模型对不同车体方案在不同速度下的水上性能进行了对比，结果表明适当增大车辆纵倾角和在裙板上增加平板薄翼有助于减少阻力。徐一新[2]基于Fluent软件对两栖车的黏性绕流场进行了数值模拟，研究了车体尾部形状对流场的影响，证明了行驶环境的改变对阻力的影响。万晓伟等[7]基于k-ε(k为湍流动能，ε为湍动能耗散率)湍流模型和流体体积函数(VOF)方法实现了良好的两栖车水上阻力预测。袁潇龙等[8]采用CFD方法研究了防浪板对两栖车水上航行性能的影响，验证了新型防浪板的减阻效果。酒永胜[9]基于CFX商业软件，采用Level Set方法模拟自由液面并采用剪切应力传输(SST)k-ω湍流模型计算两栖车迎浪直航运动，分析了航速、波高和波长等要素对两栖车航行姿态和受力特性的影响。剧冬梅等[10]同样采用CFX软件和多相流模型研究了纵倾角对两栖车阻力特性的影响，计算结果和试验吻合良好，结果表明随着航速的增加，车体纵倾角的适航范围变小，但对阻力的影响幅度变大。彭锟[11]和彭锟等[12]基于CFD技术结合代理模型，对两栖车辆外形减阻优化进行了研究，得到了车体最优航行倾角、最优长宽比等设计方法，此外还研究了加装尾翼板对航行阻力的影响，结果表明在低傅汝德数时加装尾翼板可以起到很好的减阻效果。赵彬等[13]采用k-ε湍流模型和动网格技术，研究了两栖车在静水直航中的航行姿态变化规律，模拟结果与试验吻合较好。郑翔玉等[14]采用Fluent商业软件研究了车轮收放前后对两栖车减阻增速的影响，结果表明车轮收起后，车辆水上行驶阻力减小，增速效果明显。蔡宇峰等[15]基于可实现的k-ε湍流模型、VOF方法和重叠网格技术建立了两栖车三维非定常数值模型，并与试验结果进行了对比，验证了该模型的有效性。王丽丽等[16]同样采用上述数值模型研究了尾压浪板的减阻效果，且表明VOF方法捕捉到的自由液面与实际情况较为相符。孙旭光等[17]基于CFD技术提出了以改进叠模为技术路线的形状阻力分离方法，计算结果与拖曳模型航行阻力试验结果基本吻合，建议在两栖车的总体设计中应力求优化车尾形状使得车后部收缩平缓，同时增大长宽比以减小形状阻力；车首优化时应改善与水流交界的入流角，使其尽量小以达到减小车辆兴波阻力的效果。

综上所述可知，近年来国内对两栖车的水动力性能研究主要集中在采用商业CFD软件计算两栖车在静水下的阻力和快速性等问题，以及通过大量数值模拟研究影响两栖车水动力性能的各要素并提出具体的优化方案。研究对象主要集中在单车厢两栖车的静水航行运动，而新型网格技术如重叠网格的模拟计算则较少。由于双车厢两栖车可大幅提升货物运载能力，但国内外缺乏对此类新颖的两栖车水动力学性能的设计研究，本文采用CFD方法和重叠网格技术对双车厢的实尺度水陆两栖车在静水下的直航运动响应进行数值模拟，建立多体运动的数值仿真模型，双车厢之间采用具有3自由度的球形铰接点进行连接；研究车体总阻力、纵摇和垂荡等运动性能以及球铰对前后车体在3个方向的作用力。数值计算与拖曳水池试验的总阻力结果基本一致，表明该数值模型可以较好地预报双车厢两栖车的水动力性能和运动状态；由静水海况下的计算结果可以发现，总体上双车厢两栖车的纵摇角度保持在1°以内，车体纵稳性能优良。

1 CFD模型设置

1.1 物理模型设置

本文借助CFD商业软件STAR-CCM计算双车厢两栖车在静水直航下的水动力性能。假定计算域中的水和空气均为不可压缩流体，控制方程主要包括质量守恒和动量守恒方程。采用有限体积法(FVM)进行空间离散，采用分离流模型和隐式非定常求解器求解流体方程。湍流模型选择适用于复杂几何外部流动问题求解的可实现k-ε湍流模型。自由液面的捕捉和模拟采用VOF方法[18]，通过在入口边界给定流速和液面位置的设置来模拟静水自由液面。对于静水运动问题，用流速代替车体航速，以保证车体模型在有限区域内完成较长时间的运动模拟。

1)不可压缩流体质量守恒方程

(1)

式中：vx、vy、vz分别为流体速度矢量v在x轴、y轴、z轴上的速度分量。

2)动量守恒方程(Navier-Stokes方程)

(2)

(3)

(4)

式中：ρ为流体密度，是1个常数；p为流体微元体上的压力；div为散度符号；μ为动力黏性系数，是1个常数；grad为梯度符号；fx、fy、fz分别为微元体上x轴、y轴、z轴方向的质量力，质量力只有重力，且z轴方向竖直向上，因此fx=0、fy=0、fz=ρg，g为重力加速度。

两栖车的6自由度运动模拟利用动态流体与固体相互作用模块(DFBI)求解完成。使用该方法求解需指定双车厢两栖车为多体运动，该运动模式可以确保前车体和后车体之间通过球形铰接(见图2)存在相互耦合作用。球形铰接是一种具有3个转向自由度的装置，通过球铰相互连接的物体无相对位移运动，只存在相对角度的变化，适合作为两栖车前后车体的连接装置来模拟双车厢耦合运动。流场对前后车厢的作用力均可以通过球铰联系起来。因此，单个车厢主要受到重力、流体水动力和铰接力三者的作用。两栖车运动过程中存在纵荡、横荡和垂荡3种平移运动以及横摇、纵摇和艏摇3种旋转运动，因此必须指定前后车体各自的质量和惯性矩，以及两车厢的吃水和重心位置。本文所有模拟只研究垂荡和纵摇2个方向的自由度，对于横摇运动，由于车体形状对称设计且方形系数较大，其横摇角度较小，不对其横摇运动进行分析。因此必须控制其他3个自由度的运动状态。在实际静水直航运动中，纵荡速度是固定的，因为数值模拟的计算域大小和网格数量有限，数值计算采用大小相等、方向相反的流体运动代替车体的纵向运动，并添加与运动状态有一定函数关系的外部作用力，以保证纵荡位移在计算稳定段保持在平衡位置；实际静水直航中两栖车按照一定航线行驶，其横向运动几乎不变，因此在数值计算过程中引入了控制策略，添加外部作用力，以保证横荡位移在计算稳定段保持在平衡位置；对于艏摇运动，两栖车实际直航运动中可通过控制转向装置舵使车体按固定直线行驶，因此在数值计算中通过施加外部作用力矩，以保证艏摇角度在计算稳定阶段保持在0°位置。

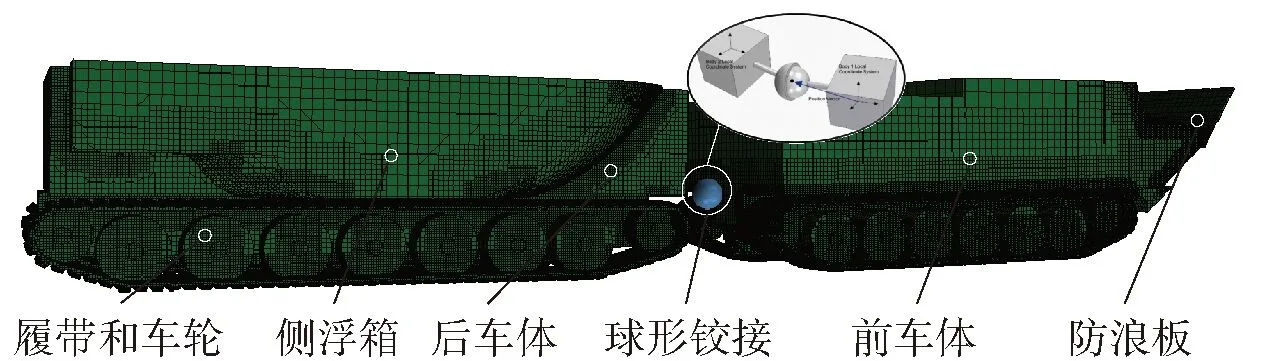
图2 双车厢两栖车计算简化模型Fig.2 Simplified model of a double-carriage amphibious vehicle

1.2 网格划分和边界条件设置

本文计算采用重叠网格技术[19-20]，计算域分为背景流域和重叠网格区域两部分，其中重叠网格域又可以分成前车厢重叠网格域和后车厢重叠网格域两部分，两两之间都设有重叠网格交界面。使用3套网格进行网格划分，总网格数为407万，各网格区域网格数量如表1所示。网格划分需考虑当地流场变化是否剧烈以及物面的复杂程度，因此本文研究的网格划分方法需在全局网格的基础上对部分区域进行网格加密操作。

表1 各区域网格数量Tab.1 Quantity of grid in each region

自由液面对计算结果的影响非常大，因此对自由液面处网格进行了加密，尤其是尾流兴波区域进行重点加密；车体物面网格，尤其是复杂位置如防浪板、履带、车轮以及侧浮箱的形状变化剧烈，需要单独设置加密区域进行网格加密；车体表面边界层网格对摩擦阻力的计算影响较大，本文计算选取y+=80进行计算，参数y+是CFD中用来计算物面处第1层网格厚度的无量纲数，在计算过程中需要根据所选择的湍流模型、流体属性、物体运动参数等因素综合确定，计算选取的边界层总厚度为5 mm；此外，物面附近流场变化比较复杂，因此需要对物面周围网格进行加密；考虑到物面周围网格尺寸与流域网格基础尺寸之间差异较大，需在背景计算域内设置网格过渡区域进行网格逐层过渡细化，一般网格以2倍变化率进行过渡，但要注意最好保持过渡区域的网格尺寸和重叠区域的网格尺寸一致。本文网格划分采用自动网格划分方式，最终的网格划分截面示意图如图3所示。

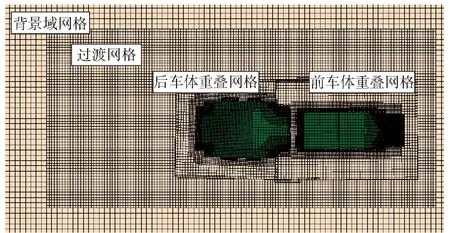
图3 网格划分示意图Fig.3 Schematic diagram of meshing

边界条件的选择对计算结果也有十分重要的影响。本文研究的流域边界条件由5个速度入口和1个压力出口组成，对于速度入口均给定两栖车航速，方向与车体运动方向相反；车体物面设置为无滑移壁面边界条件；自由液面采用VOF方法设置静水面。为了减弱由于出口数值反射造成的回流现象，在距离压力出口6 m范围内采用VOF波阻尼方法进行消波，具体的边界条件设置如图4所示，图中L为两栖车的车身长度。

图4 边界条件设置Fig.4 Setup of boundary conditions

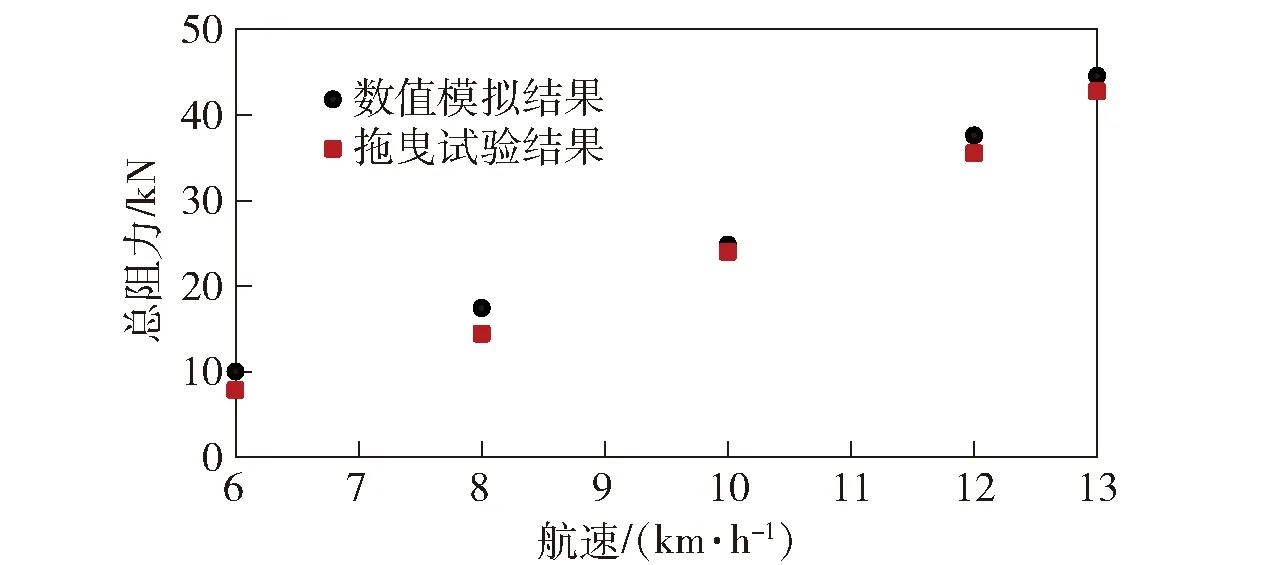
图5 数值模拟与拖曳试验结果对比Fig.5 Comparison of numerically simulated result and model towing test result

综上所述，本文使用基于有限体积法的CFD流体计算软件STAR-CCM+，采用可实现的k-ε湍流模型和重叠网格技术建立了以球铰方式连接的双车厢两栖车多体运动数值模型。基于该数值模型计算了6 km/h、8 km/h、10 km/h、12 km/h、13 km/h共5种航速下的静水总阻力，并与船模拖曳水池的试验结果进行了对比，如图5所示。拖曳试验在大连理工大学船模拖曳水池完成，试验样机如图6所示，模型试验的结果根据傅汝德数相似条件换算到实尺度上。由图5可以看出，数值计算的总阻力与试验结果基本一致，低航速下的相对误差较大。考虑到两栖车的履带等复杂结构导致建模过程存在简化，本文研究的计算误差仍在合理范围内，因此该模型可以用于两栖车的水动力性能计算。

图6 两栖车模型拖曳试验Fig.6 Towing test of an amphibious vehicle model

2 双车厢两栖车水动力性能研究

两栖车在静水中的直航运动模拟需采用VOF方法来建立自由液面，需指定气体与液体两相流体属性、水线位置、流速大小和方向。本文研究计算了两栖车在静水下的阻力、纵摇、垂荡运动以及球铰3个方向的受力情况。图7所示为典型工况12 km/h航速下两栖车的阻力系数变化时程曲线，本文均选取计算稳定段内10 s的计算结果平均值进行对比研究。车体航速包括6 km/h、8 km/h、10 km/h、12 km/h、13 km/h共5种，各航速下水动力性能的计算结果分别如图8～图10所示。对于低航速工况，两栖车的运动性能计算可以更快速地达到稳定状态。此外，本文以典型工况12 km/h航速为例，研究了球铰在x轴、y轴、z轴3个方向对前后车体的作用力情况，其中x轴方向为车尾指向车头的纵向方向，y轴方向为沿车宽的横向方向，竖直向上为z轴方向(见图4坐标系)。计算结果的时程曲线如图11～图13所示。

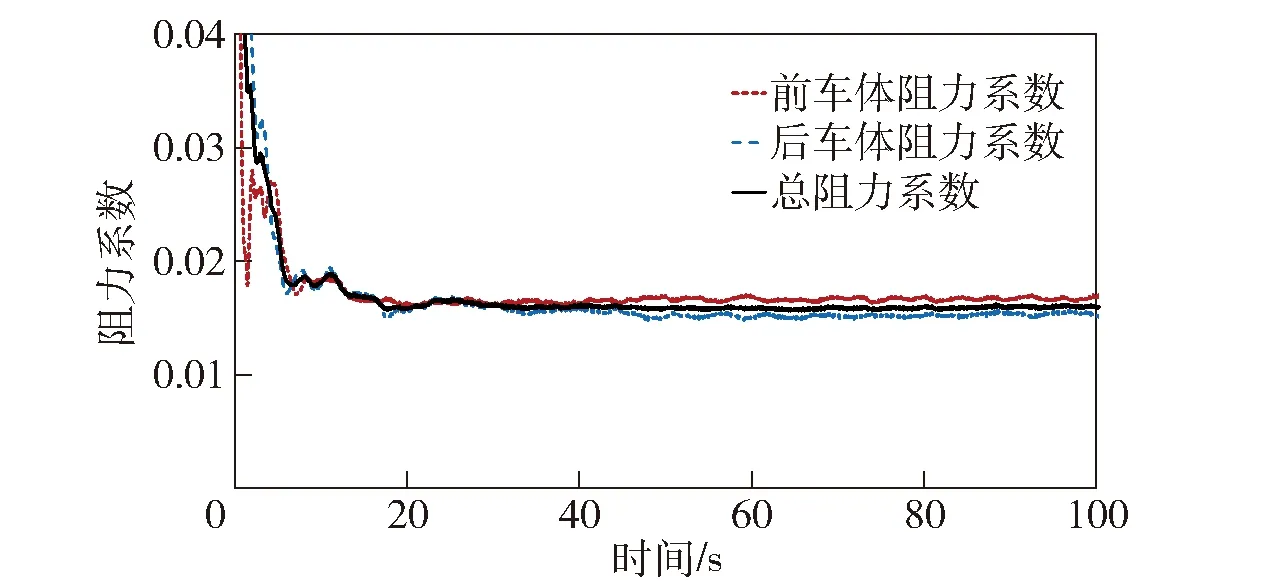
图7 12 km/h航速下阻力系数时程曲线Fig.7 Drag coefficient versus time at 12 km/h

阻力系数的计算公式为

(5)

式中：Cd为两栖车的阻力系数；Fd为两栖车总阻力；S为两栖车水下的湿表面积。

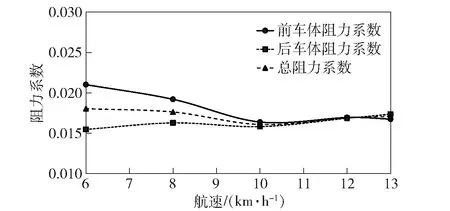
图8 阻力系数计算结果Fig.8 Calculated results of drag coefficients

图9 纵摇运动计算结果Fig.9 Calculated results of pitching motions

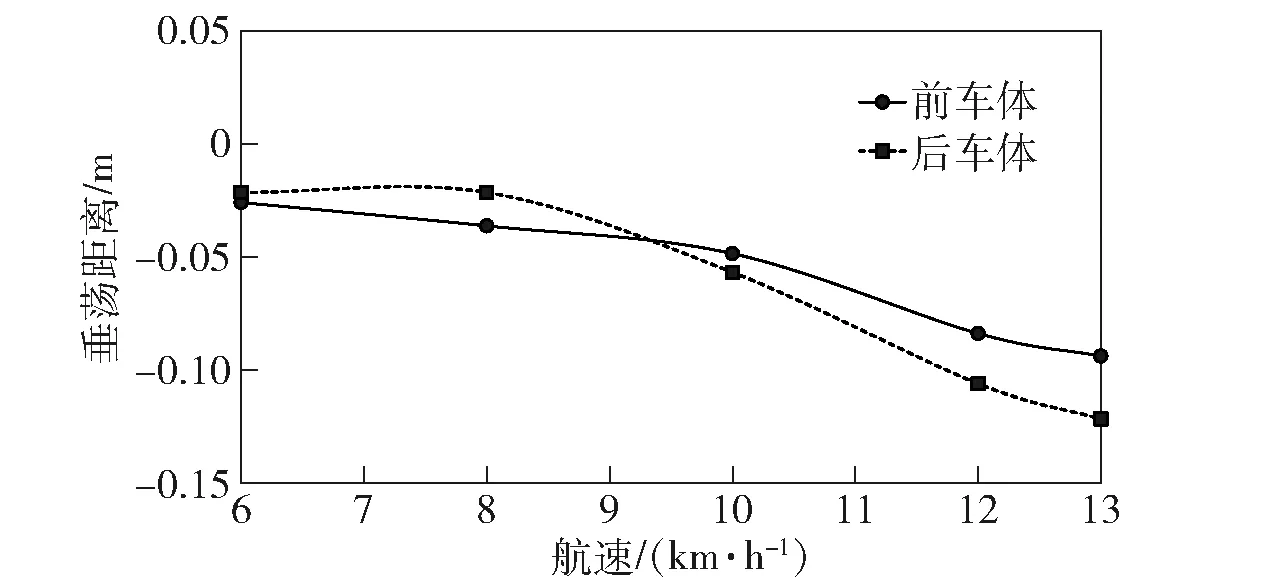
图10 垂荡运动计算结果Fig.10 Calculated results of heaving motions

图11 12 km/h航速下球铰x轴方向作用力时程曲线Fig.11 Applied force of spherical joint in x-direction at 12 km/h

图12 12 km/h航速下球铰y轴方向作用力时程曲线Fig.12 Applied force of spherical joint in y-direction at 12 km/h

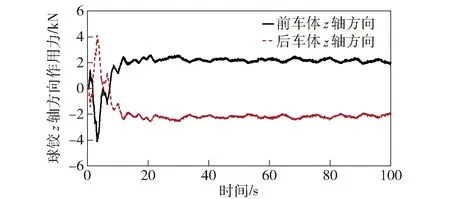
图13 12 km/h航速下球铰z轴方向作用力时程曲线Fig.13 Applied force of spherical joint in z-direction at 12 km/h

由图8可知，两栖车的阻力系数是较大的，原因主要是车体型线是非流线型的，方形系数大，且水下湿表面积较大，导致产生较大的压差阻力和摩擦阻力。由图9可知，两车厢在球铰连接的情况下通常保持中垂或中拱状态，以埋首方向为纵摇正方向，低航速下前车体埋首而后车体仰首，高航速下前车体仰首而后车体埋首，原因是高航速下倾斜的防浪板提供了较大升力。此外，总体上可以看出前后车体的纵摇角度均保持在1°以内，车体纵稳性能优良。由图10可知，两栖车航速越高，车体平均下沉深度越大，且前后车体的垂荡值相近，原因主要是周围流速的增大导致车体上下压差变大，因此车体吃水在高航速下会增加。

由图11～图13可知，静水直航稳定状态下，以一定控制策略施加外力(螺旋桨推力)作用时，球铰在x轴方向对前后车体的作用力可以达到很小。在实际两栖车航行时，因为前后车体自身均配置有推进器，所以可通过调节各自推进器的转速，以使得铰接装置在纵向受力最小；在y轴方向的作用力在稳定段的波动幅值较大，原因可能是前后车体的横荡运动不同步造成的；在z轴方向的作用力较大，主要是前后车体埋首方向不一致，导致两栖车总体上出现中垂或中拱现象引起的，工程中需重点考量z轴方向作用力对球铰的影响。需要说明的是，两栖车在回转运动中水平方向(x轴和y轴方向)会产生较大的作用力，此外，两栖车在波浪中的运动对球铰垂向(z轴方向)作用会更大，因此实际工程中需要结合多种运动状态和海况条件来设计铰接装置。

3 结论

本文基于CFD方法和重叠网格技术建立了以球铰方式连接的双车厢两栖车多体运动数值模型，采用VOF和DFBI方法实现了两栖车在静水海况下的多自由度直航运动状态模拟，并与两栖车样机模型的拖曳试验结果进行了对比；获得了两栖车的阻力、纵摇角、垂荡距离和球铰3个方向受力数据并进行了比较。得出主要结论如下：

1)数值计算与拖曳水池试验的总阻力结果基本一致，表明采用可实现的k-ε湍流模型、重叠网格技术以及球铰连接方式建立的数值模型，可以较好地实现双车厢两栖车的水动力性能预报。

2)低航速下前车体埋首而后车体仰首，高航速下前车体仰首而后车体埋首，原因主要是高航速下倾斜的防浪板提供了较大升力。总体上可以看出，双车厢两栖车的纵摇角度保持在1°以内，车体纵摇性能优良。

3)在静水直航工况中，前后车体的纵摇结果表明两车厢在球铰连接的情况下通常保持中垂或中拱状态，因此导致球铰在z轴方向对前后车体的作用力最大，球铰和对应的连接杆件设计需重点考虑z轴方向的作用力问题。

4 展望

水陆两栖车在水中速度一般可达到12～13 km/h[1]，两栖车目前存在的一个较大问题就是如何提高水中航速，解决该问题可以通过改进水下推进装置增加推力、增加车轮收放装置以及优化车体尤其是车头的型线设计以降低车身阻力等方法实现；另一个问题是如何改善水动力性能，主要是减小纵倾和垂荡运动，改善措施主要包括优化防浪板形状与安装角度、增加减摇装置或者优化车身设计等。

对于排水量较大的双车厢两栖车，这类问题同样亟待解决，未来的工作将主要采用CFD数值模拟方法实现两栖车的优化设计，并结合少量模型试验来改善其水动力性能。此外，目前对于两栖车回转性能和耐波性能的研究较少，这也是未来工作的重点。