弹道枪水下全淹没式发射膛口流场演化特性的数值模拟研究

2020-04-16张京辉余永刚

兵工学报 2020年3期

张京辉，余永刚

(南京理工大学能源与动力工程学院，江苏南京 210094)

0 引言

地球表面海洋区域广大，具有重要的经济和战略意义。为了适应未来战争的需要，水下枪炮的研究逐渐成为热点。与在空气中发射不同，水下发射条件会对膛口流场产生较大影响，因此，研究枪炮在水下发射条件下的膛口流场是十分必要的。

众多学者针对枪炮在空气中发射的膛口流场做了大量实验与数值研究。Schmidt等[1]采用实验方法测量了初始流场对膛口气流参数的影响。Steward等[2]利用1 600 Hz高速相机对榴弹炮的膛口流场作用时间和作用范围进行了研究。Watanabe等[3]分别采用二维和三维非稳态Euler方程，耦合动网格法和有限状态自动机(FSA)算法，对弹头穿越前方激波所诱导的流场进行了数值模拟。朱冠南等[4]通过低压舱模拟高空环境，测量了7.62 mm步枪在低压环境下发射的膛口冲击波压力。郭则庆等[5-6]搭建了小口径武器膛口流场的观测系统，运用直接阴影法获得了高分辨率膛口流场照片，并运用数值模拟方法研究了初始流场对火药燃气流场的影响。李子杰等[7]对超高速火炮膛口流场特性进行了仿真研究。吴伟等[8]基于无网格方法，对包含大位移运动边界和非平衡化学反应膛口流场进行了数值模拟。陈川琳等[9]结合实验与数值模拟，研究了弹头在膛口流场中的受力情况和运动规律。

在水下膛口流场方面，张欣尉等[10-11]对机枪在空气中和水下密封式发射所形成的膛口温度场进行了数值对比分析。水下膛口流场涉及到气体与液体两相流相互作用问题，围绕燃气射流与水的作用，许多学者进行了实验与数值模拟研究。Xue等[12]设计了5级圆柱渐扩型观察室，观察了双股燃气射流在液体工质中的扩展过程。Hu等[13]和Zhao等[14]分别针对壁面射流和锥形分布射流在受限圆管内的燃气扩展过程进行了实验和数值模拟研究。Zhou等[15]用高速摄影装置观察并记录了燃气射流在圆柱形充液室中与液体相互作用的过程。Zhang等[16]搭建了水下气幕式发射平台，通过将弹后燃气引导至弹前形成气幕排水，实现了水下低阻发射。

综上所述，已有研究主要针对空气中的膛口流场和水下燃气射流，但对水下弹道枪在全淹没发射条件下(即身管内充满水)的膛口流场研究相对较少。本文以12.7 mm滑膛式弹道枪为平台设计水下射击实验系统，观察并记录水下弹道枪全淹没式发射膛口流场演变的过程，并对实验工况进行数值模拟。所得研究结果对于研究新型水下枪炮设计、新型水下发射方式有一定的参考价值。

1 实验测试系统

本文设计的水下弹道枪全淹没式发射的实验测试系统如图1所示,图2为部分实验装置的实物图。实验系统由水箱、12.7 mm弹道枪、水泥平台以及脉冲电点火器组成。其中水箱上开有射击孔，供身管伸入，水箱侧面开有观察窗。用日本PHOTRON公司生产的FASTCAM-Ultima APX高速摄像机与计算机进行流场演化过程的记录，其中高速摄像机最大分辨率为1 024×512像素，频率为4 000帧/s.

图1 实验装置示意图Fig.1 Schematic diagram of experimental device

图2 实验装置部分实物图Fig.2 Physical photograph of experimental device

在实验准备阶段，将弹头填充在枪膛底部，通过弹带进行密封以阻止水进入弹后燃烧室；为保证全淹没发射环境，将身管以及水箱内注满水；调整高速摄像机拍摄的焦距与角度，使其能透过观察窗清楚地拍摄到膛口流场区域；当仪器调整好后，将称量好的火药装入燃烧室，装好电底火，并将其连接到脉冲电点火器上。所有装置就绪后，用脉冲电点火器放电进行点火。实验后，用计算机将高速摄像机拍摄的结果进行截取和后处理。

2 数理模型与计算方法

2.1 物理模型

根据水下全淹没式发射特点，对12.7 mm滑膛式弹道枪水下全淹没式发射过程采用下列物理模型：

1)火药燃烧遵循几何燃烧定律。

2)药粒均在平均压力下燃烧，且遵循指数燃速定律。

3)用次要功系数来考虑其他次要功。

4)单位质量火药燃烧所放出的热量及生成的燃气温度均为定值，在以后的膨胀做功过程中不考虑燃气组分变化，火药力、余容及比热比等均视为常数。

5)将膛口燃气流场在水下的扩展过程看作是一个二维轴对称非稳态过程；湍流模型采用标准k-ε模型，k为湍动能，ε为耗散率。

6)将高温火药燃气看作理想气体，不考虑燃气在膛口的二次反应，忽略体积力的影响。

7)假设水为不可压缩相，密度取998.2 kg/m3.因膛口燃气流与水的作用时间短暂，忽略燃气射流对水的汽化作用。

8)弹前水柱出膛后空化采用Schnerr-Sauer模型，假设水蒸汽为不可压缩相,密度取0.554 2 kg/m3.

2.2 数学模型

针对上述物理模型建立下列数学模型。

1)连续性方程

(1)

式中：q分别为g、l、v，g、l、v分别表示燃气相、液相和水蒸汽相；αg、αl、αv分别表示燃气相、液相和水蒸汽相的体积分数，且αg+αl+αv=1；ρq表示对应项的密度(kg/m3)；uq为流体速度；Sm为单位体积内汽相与液相之间质量交换量，这一项在水与蒸汽相发生质量输运时才有，当各相之间不发生质量输运时此项为0.

2)动量守恒方程

(2)

式中：pq表示对应项的压力(Pa)；Sp表示汽相与液相间质量输运引起的动量变化，此项在水与蒸汽相发生质量输运时才有，当各相之间不发生质量输运时此项为0.

3)能量守恒方程

(3)

(4)

(5)

式中：ρ为混合相密度；E为平均能量(J)；p表示混合相压力(Pa)；T为平均温度(K)；keff为有效热传导率(W/(m2·K))；Se为能量方程源项，即空化引起的流场能量的改变，其大小等于单位体积内汽相与液相之间质量交换量与汽化潜热的乘积(J/(m3· s))。

4)气体状态方程

p=ρRT，

(6)

式中：R为火药气体常数，R=319.6 J/(kg·K)。

5)k-ε湍流方程

(7)

(8)

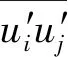
6)Schnerr-Sauer空化模型

(9)

(10)

式中：Γe和Γc分别表示气泡生长和溃灭时质量传递源项；Rb为气泡的半径，

(11)

c为单位液体体积所包含的空泡个数。

膛口流场的计算中需要耦合内弹道方程组，内弹道方程如下：

1)形状函数

(12)

式中：ψ为火药燃烧百分比；χ、λ和μc分别为火药形状函数；Z为火药燃烧相对厚度；Zk为颗粒燃尽时燃烧相对厚度；χs和λs分别为多孔火药分裂后的形状函数。

2)燃速方程

(13)

式中：uh为火药燃速系数；n为火药燃速指数；eh为火药半弧厚；t为时间。

3)弹头运动方程

(14)

式中：pd和pf分别为弹底和弹前压力：A为弹头横截面积：φ为次要功系数：m为弹头质量：v为弹头运动速度。

4)内弹道基本方程

(15)

(16)

式中：lψ为药室自由容积缩径长；x为弹头行程；θ为比热比，θ=kr-1，kr为比热比；f为火药力；ω为装药质量；l0为药室容积缩径长；α为余容；Δ为装填密度；ρp为火药密度。

5)弹头速度与行程关系式

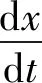
(17)

2.3 计算方法

数值模拟借助Fluent软件，结合用户自定义函数(UDF)，耦合内弹道方程组求解得到弹丸速度、位移和膛压；采用流体体积函数(VOF)多相流模型描述气液相互作用；利用PRESTO!方法对压力项离散；动量和能量的离散采用1阶迎风格式；采用压力隐式拆分(PISO)算法[8]对压力与速度进行耦合；计算采用的时间步长控制在0.2 μs内。

3 网格划分与无关性验证

3.1 网格划分

如图3所示，计算域分为身管区域和膛口流场区域2个部分，其中身管区域为长1 m、半径为6.35 mm的圆柱形区域，流场区域为长1 m、半径为0.3 m的圆柱形区域。以结构化网格为主，对膛口附近的网格进行局部加密，最小网格尺寸为0.3 mm×0.3 mm.弹头运动会导致网格变形，因此采用动网格技术中的层铺法。随着弹头向前运动，当靠近弹底的网格长度被拉长至0.6 mm时，网格会分裂成2个网格。同理，当靠近弹头的网格长度被压缩至0.2 mm时，该网格会与相邻的网格合并。

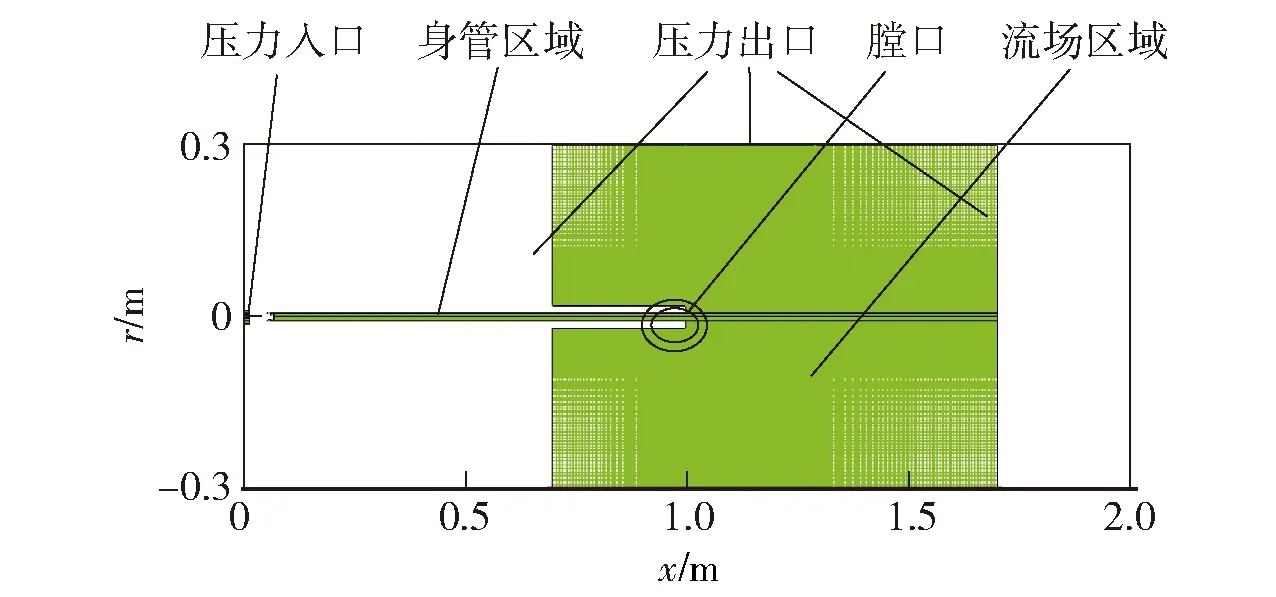
图3 计算域及边界条件Fig.3 Calculational domain and boundary conditions

本文计算的边界条件为：燃烧室为压力入口，其初始参数由内弹道方程组求解得出；身管壁面及弹丸为固壁边界；计算域外边界为压力出口，压力为环境压力。将弹前身管区域与流场区域初始化为充满水，温度与压力初始化为环境条件，即温度为300 K，压力为101 325 Pa.

3.2 网格无关性验证

网格无关性验证结果如图4所示，分别采用20万、15万和10万的网格数N进行验证。选择弹丸出膛后1 ms时刻膛口中心温度沿轴向变化情况进行网格无关性验证。相对于20万网格数的计算结果，15万网格数的最大相对误差为2.8%，10万网格数的最大相对误差为6.6%.综合考虑计算效率和计算精度，现选择网格数为15万的网格进行计算。

图4 膛口中心温度沿轴向变化曲线(弹头出膛后1 ms)Fig.4 Temperature curves of muzzle center along the axial direction(1 ms after a bullet exits from the bore)

4 结果与分析

4.1 实验结果

弹道枪水下全淹没发射条件下膛口流场的发展过程如图5所示。由于身管水柱空化的影响，无法直接观察到弹头出膛瞬间，将在膛口能观察到气体产生的时刻定为t0时刻。由图5可见，点火后，弹头如同活塞般不断推动弹前水柱，使水柱具有较高的速度。水柱出膛口后，局部压力降低，空化产生水蒸汽，如图5(a)所示。随着弹前水柱的不断运动，空化产生的水蒸汽逐渐增多，在膛口堆积，如图5(b)所示。弹头出膛口后，膛内的火药燃气流出膛口，与水蒸汽掺混在轴向与径向上迅速扩展，很快追上并包裹弹头，射流的外部轮廓变得不规则，如图5(c)所示。随着弹头运动到射流头部，射流头部逐渐变尖，如图5(d)所示。当弹头头部已经超越射流时，对射流在轴向上的约束减小，使射流在轴向上迅速扩展，而在径向上扩展仍受水环境的限制，因此头部呈锥形，如图5(e)所示。图5(f)中弹头已完全超越射流，弹头表面不断空化产生水蒸汽，形成超空泡，同时在弹头尾部会留下细长的气柱。

图5 全淹没发射典型工况照片阴影图Fig.5 Photos of typical submerged firing working condition

图6 实验照片阴影图(上)与模拟相图(下)对比情况Fig.6 Experimental shadow photo (upper) and simulated phase diagram (lower)

图5的实验结果清楚地显示了弹道枪水下全淹没式发射时膛口流场的演变过程。由于实验中流场内部的温度、压力等参数无法直接测量，建立二维多相流模型，针对实验工况进行了数值模拟，用以对实验结果的补充。图6、图7所示为实验结果与数值模拟结果的对比情况。由图6可见，模拟结果中不同时刻射流的外部轮廓与实验照片阴影图吻合较好；由图7可见，模拟结果中不同时刻燃气射流的轴向、径向最大位移与实验测量值吻合较好，最大相对误差为5%，表明本文采用的数值模型基本合理。从图6(a)中可以确定弹头即将出膛口时刻，在本文之后的讨论中将此时刻定义为0 ms时刻。

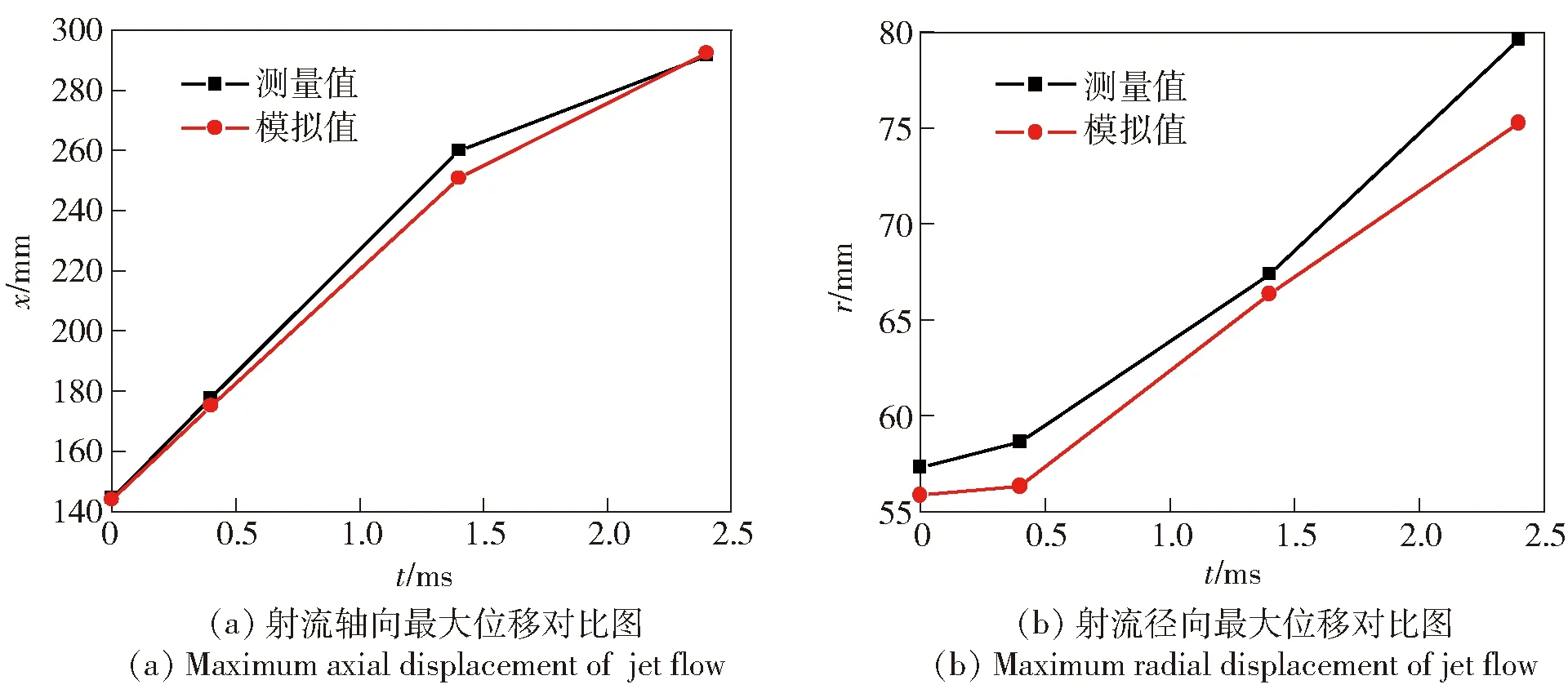
图7 射流轴向、径向最大位移对比图Fig.7 Comparison of axial and radial displacements of jet flow

4.2 计算结果与分析

4.2.1 蒸汽发展和演化过程分析

将弹头即将出膛口时刻定义为t=0 ms时刻，相应地，将弹头在身管内运动的时刻定义为负时刻，例如将弹头出膛前2 ms时刻定义为t=-2.0 ms.在水下全淹没发射过程中，由于弹头相对于水做高速运动，使得局部水压降低至水的饱和蒸汽压力以下，从而空化产生水蒸汽，形成空泡。为了解膛口流场中水蒸汽发展和演化过程，图8给出了膛口中心剖面蒸汽相图。

由图8(a)和图8(b)可见，点火后弹头推动身管内的水柱不断加速，使膛口附近的局部压力低于水的饱和蒸汽压力，膛口附近的水不断汽化为水蒸汽，在膛口逐渐堆积成一个蒸汽团。由图8(c)可见,在t=0 ms时刻，弹头头部被侧面的蒸汽团完全包裹。随后t=0.2 ms时刻，高压火药燃气由膛内流出，与蒸汽团迅速掺混，提高了膛口附近的压力，使得蒸汽团迅速溃灭。同时弹头穿过蒸汽团后相对水介质做高速运动，使得弹头头部表面水的压强降低，初步形成自然空泡。由图8(e)～图8(h)可见,弹头出膛1.0 ms后，随着弹头继续向前飞行，弹头表面的空泡长度逐渐变长，形成超空泡，包裹着弹头前进。

4.2.2 波系结构分析

由于膛内的火药燃气处于高温高压状态，当燃气从膛口流出后，会迅速膨胀并与高密度水介质以及弹头相互作用，从而形成复杂的波系结构。为了解弹道枪水下全淹没发射条件下膛口流场的波系结构与演化特性，图9给出了膛口中心剖面的密度云图与等值线图。

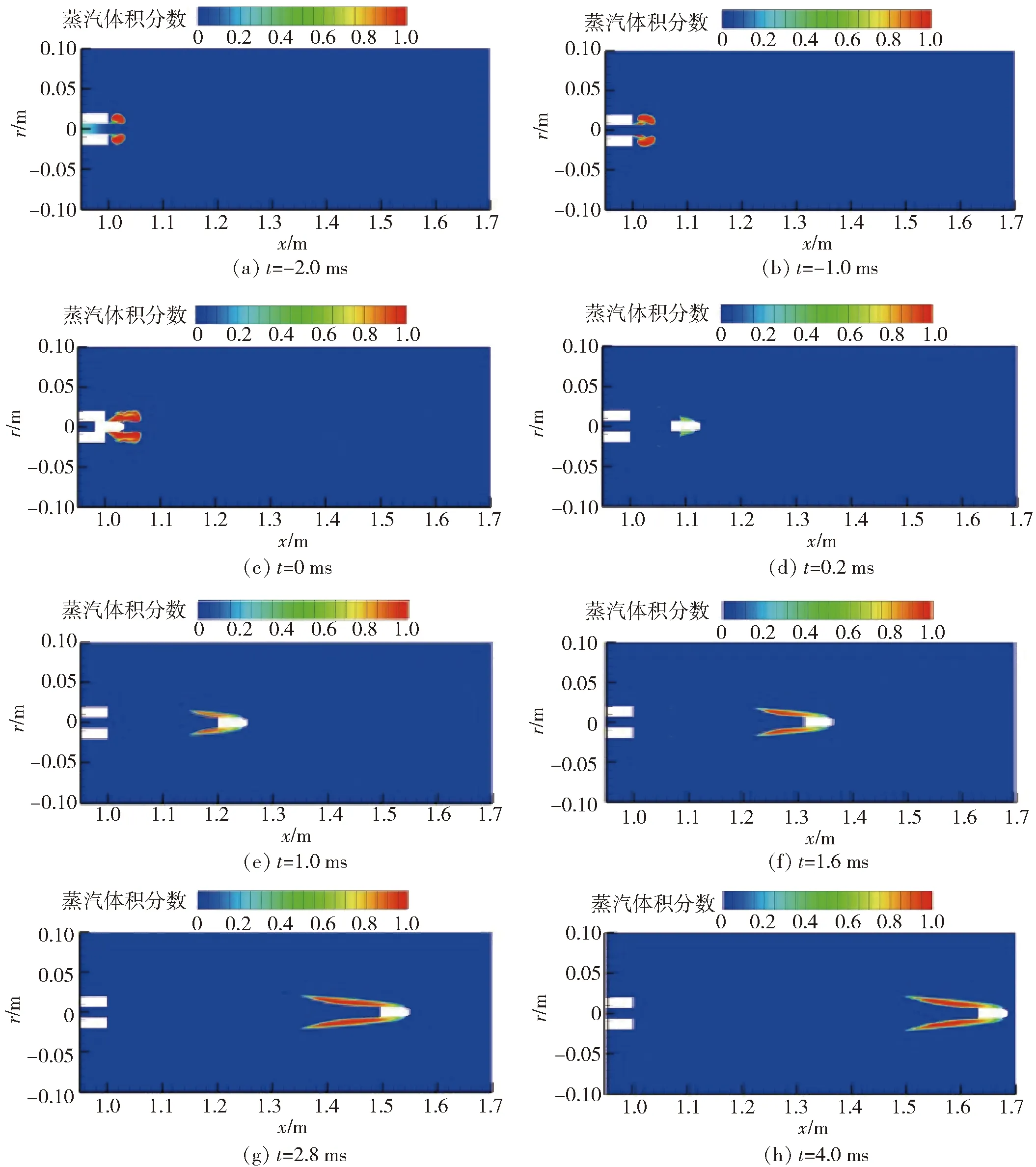
图8 膛口中心剖面蒸汽相图Fig.8 Vapor phase diagram of muzzle center

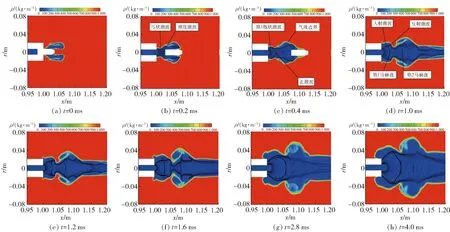
图9 膛口中心剖面密度云图与等值线图Fig.9 Density nephogram and contour map of muzzle center

由图9(a)可见，t=0 ms时刻弹头即将飞出膛口，弹前的高速水柱空化产生的水蒸汽包裹着弹着头部。在图9(b)中，随着弹头飞出膛口，膛内的高度欠膨胀火药燃气流出膛口后，由于膛口近场空化水蒸汽的存在，其密度比水小得多，易使火药燃气在轴向与径向上迅速扩展，从而加速了膛口燃气流场的形成。由于弹头的约束，燃气在轴向上膨胀受限，在膛口附近形成一道弓状激波，在弹底形成了弹底激波。t=0.4 ms时刻弹头头部即将脱离膛口气团的包裹，水在弹头表面空化产生水蒸汽。弓状激波演变成包含入射斜激波、马赫盘、三波点及反射激波的瓶状激波结构，与此同时在马赫盘与弹底之间出现了一道正激波，如图9(c)所示。

在图9(d)中，随着弹头已超越膛口气团，弹底激波几乎消失。膛口的瓶状激波结构更加清晰，马赫盘的直径逐渐增大。在马赫盘下游，正激波的直径逐渐增大，演变成第2个马赫盘，与射流边界附近的斜激波相交，形成第2个瓶状激波结构，故称膛口的瓶状激波结构为第1瓶状激波，下游的为第2瓶状激波。

4.2.3 温度与压力特性分析

随着弹头逐渐飞离膛口，不再限制射流扩展，燃气射流仅在外部水环境的限制下进行膨胀。由于膛内后续的高度欠膨胀燃气不断流出，使第1个瓶状激波结构不断扩展，第1个马赫盘的直径也随时间增大。由于失去了弹头的约束，燃气射流在轴向上的阻碍大大减小，燃气膨胀更加充分，使得第2个马赫盘逐渐消失，第2个瓶状激波结构不复存在，如图9(e)～图9(h)所示。

为了明晰水下全淹没发射条件下膛口压力与温度分布特性，图10、图11分别给出了不同时刻膛口中心剖面的压力云图与温度云图,图12给出了膛口中心压力与温度沿轴向的分布曲线。

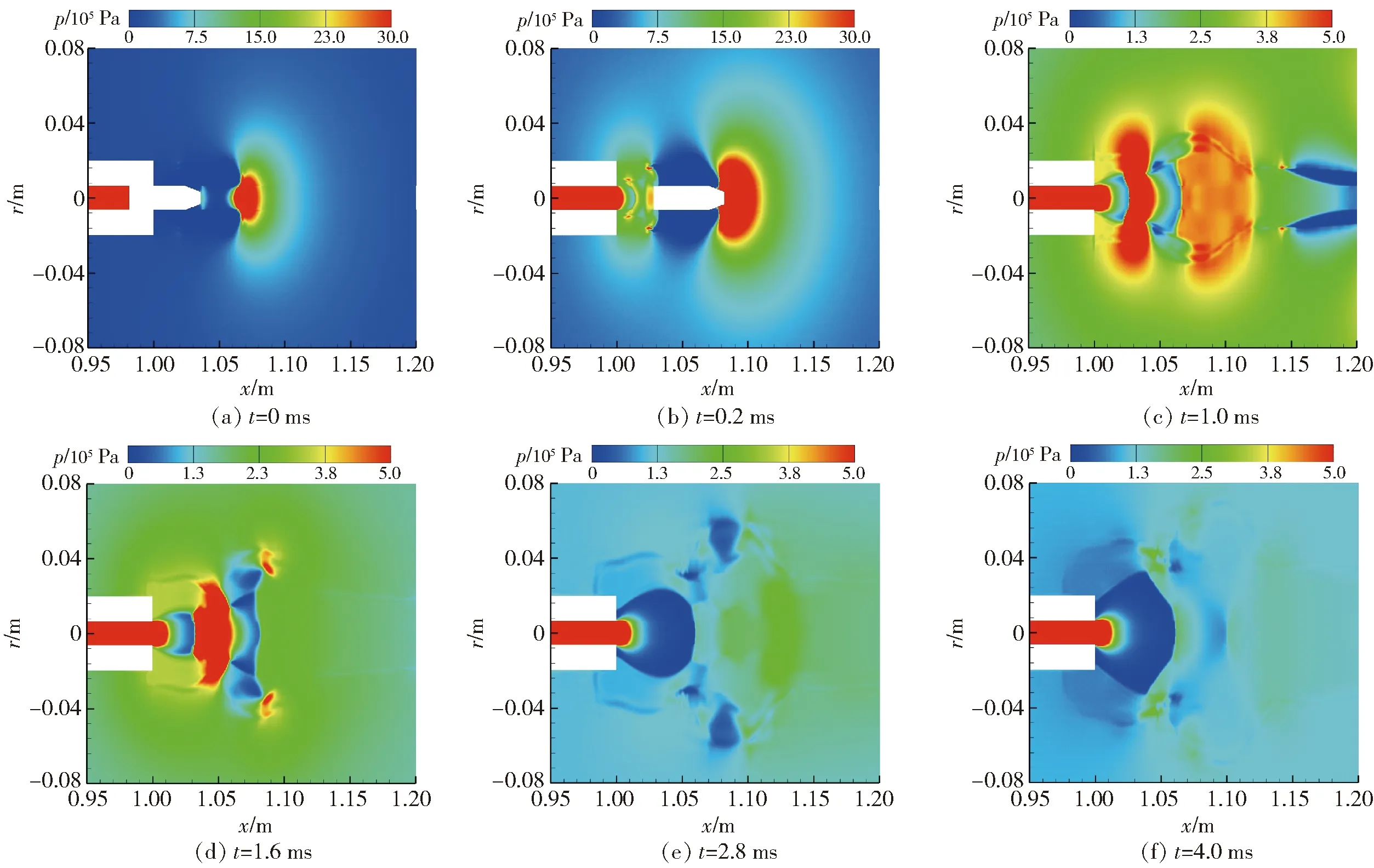
图10 膛口中心剖面压力云图Fig.10 Pressure nephogram of muzzle center

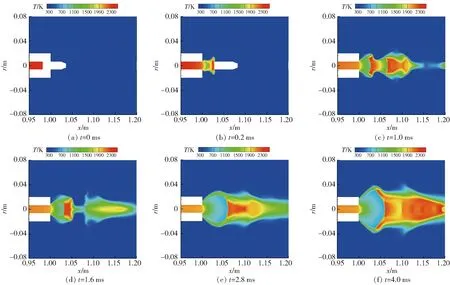
图11 膛口中心剖面温度云图Fig.11 Temperature and pressure nephogram at muzzle center

图12 膛口中心压力与温度的轴向分布曲线Fig.12 Axial distribution curves of pressure and temperature at muzzle center

由图10～图12可见，水下全淹没式发射条件下，在弹头出膛前，膛内的燃气温度达到2 000 K，压力达到14 MPa，属于高度欠膨胀气体。弹前高速水柱出膛口后，局部压力降低，空化产生了水蒸汽，这一过程对膛口附近温度的影响并不明显。弹头出膛后，膛内的火药燃气流出，在弹头和水环境的约束下膨胀，逐渐形成了包含两个瓶状激波的复杂激波结构，从而影响了膛口的温度与压力分布。第1个瓶状激波内是燃气射流的主要膨胀区，射流在瓶区内迅速膨胀，压力与温度剧降，速度激增，为超声速区。射流在经过第1个马赫盘后压力与温度陡增，速度骤减，形成亚声速区。在亚声速区的下游射流再次经历膨胀后被压缩的过程，即在第2个瓶区内迅速膨胀压力与温度剧降，速度激增，在第2个马赫盘处被压缩，压力与温度陡增，速度骤减。

弹头飞离膛口后，不再限制射流扩展，燃气射流仅在外部水环境的约束下进行膨胀。由于膛内后续的高度欠膨胀燃气不断泄出，使第1个瓶状激波结构不断扩展，内部燃气的温度与压力仍然较低。由于失去了弹头的约束，燃气射流在轴向上扩展的阻碍大大减小，燃气膨胀更加充分，使第2个瓶状激波内部燃气的温度与压力升高，第2个马赫盘与第2个瓶状激波结构逐渐消失。

为进一步研究马赫盘随时间扩展的规律，图13给出了膛口第1个马赫盘位移随时间变化情况。对其位移随时间变化特性进行拟合，发现其位移随时间满足指数上升规律为

x1(t)=24+36/(1+10(1.988-t)1.67)，

(18)

式中：x1(t)为距膛口位移(mm)，膛口为位移原点；时间t的单位为ms.

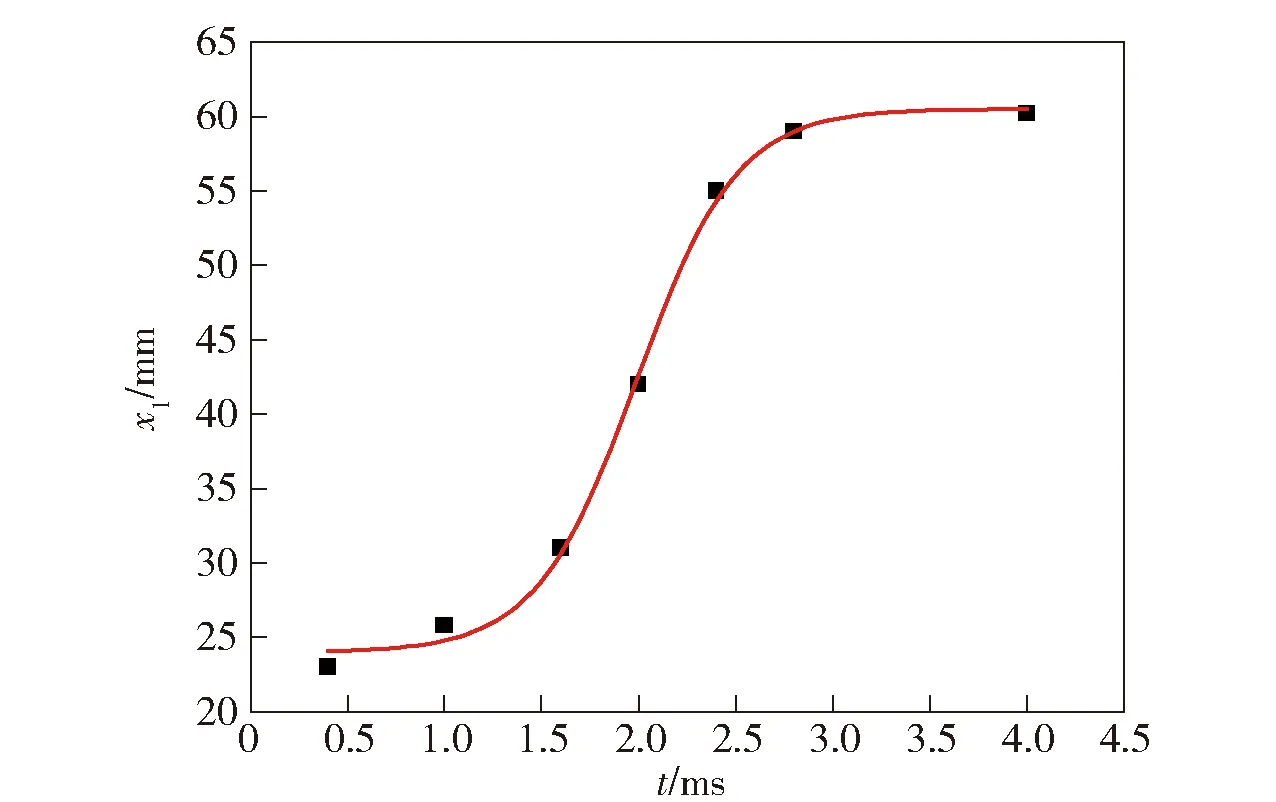
图13 膛口第1个马赫盘位移随时间变化曲线Fig.13 Position of the first Mach disk versus time

4.2.4 流场对弹体的速度影响分析

为了解在水下全淹没发射条件下膛口流场对弹体速度的影响，图14给出了弹头速度随弹头距膛口位移变化曲线。

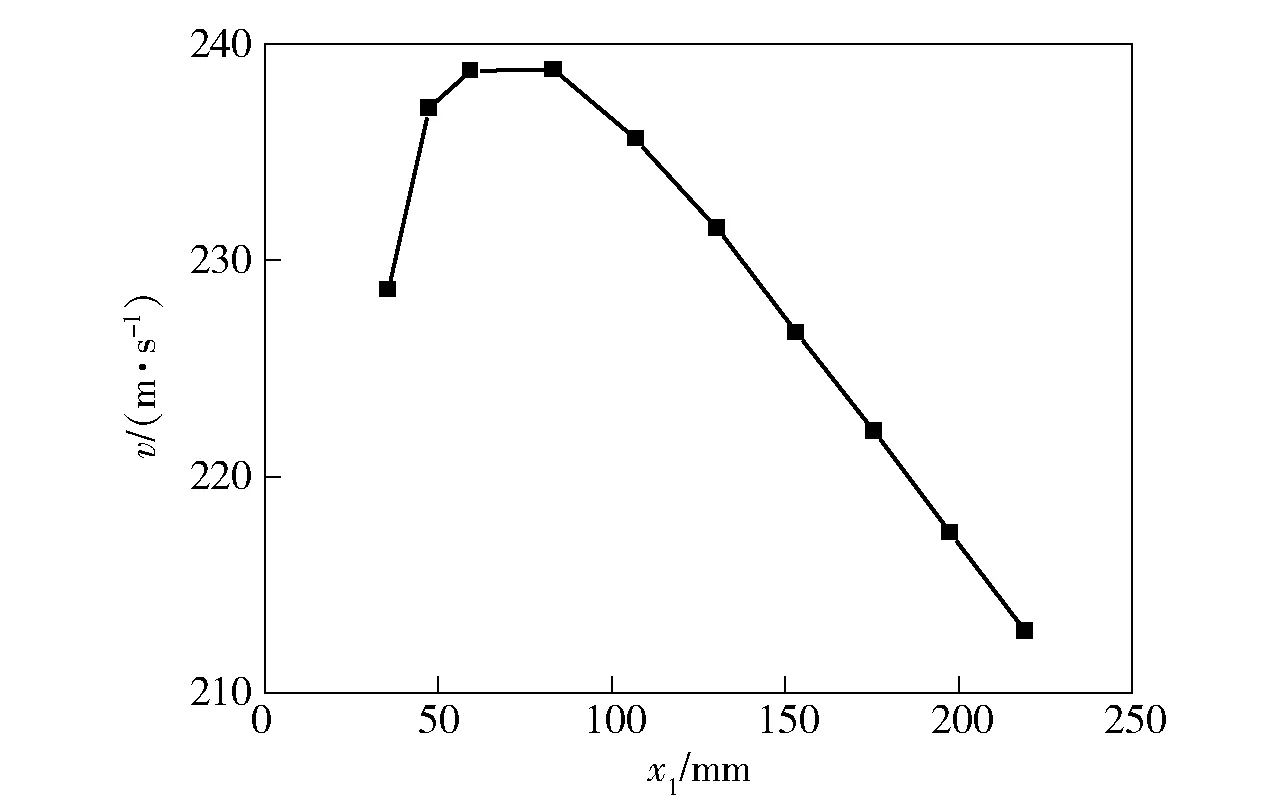
图14 弹头速度随弹底距膛口位移变化曲线Fig.14 Bullet velocity curve

由图14可见，弹头在水下全淹没发射条件下，出膛后同时受到弹前水环境的阻力和弹后高速燃气的冲击。弹头出膛后，在膛口流场影响范围内(距膛口位移x1<85 mm)，由于膛口近场空化水蒸汽的密度比水小得多，减小了弹前阻力，同时受到弹后高速燃气冲击弹底形成的弹底激波影响，使得弹头不断加速，在弹底距膛口85 mm处达到最大，为232.7 m/s.随着弹头远离膛口流场区域(x1>85 mm)，在弹前水环境阻力的作用下，弹头速度不断衰减。