基于目标打击任务的精确制导弹药优化分配模型*

刘 博，周文明，刘 钊，王如生

(1 75837部队，广州 510600； 2 国防大学联合勤务学院， 北京 100000)

0 引言

目标打击[1]任务主要通过选择相应的精确制导弹药[2]实现。精确制导弹药种类多、打击精度高、造价昂贵。制导弹药的选择需要综合目标打击要求、目标特性、弹药性能、弹药数量、经济效益等多方面因素。文中以最小化经济成本前提下完成目标打击任务为出发点，基于整数线性规划[3]建立了精确制导弹药优化分配模型，该模型能够根据制导弹药现有数量、弹药成功发射概率计算分析当前可成功发射弹药量，并结合目标打击任务要求提出经济成本最低的弹药使用分配方案。

1 模型构建

已知条件：根据弹药弹头和弹体的不同，将弹药分为N型，第i型弹药可用数量为di；根据目标本身特性和目标打击要求，将敌目标分为L类，某任务需要打击第j类目标数量为tj；效能分析推荐量xji，该物理量综合目标特性、制导弹药毁伤能力、战场环境三大影响因素，通过仿真计算的方法得到，表示只使用第i型弹药打击单个第j类目标时达成毁伤效能需要成功发射的弹药数量，当xji=∞时表示该型弹药不能够用于打击相应目标；第i型弹药单发可成功发射的概率为pi，pi可通过平时发射情况进行统计；第i型弹药单价为ci。

求解问题：打击第j类目标需要成功发射第i型弹药的数量yji。

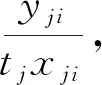
(1)

②当0≤σi<1时，μi-σi>μi-1，则P{K≥μ-1}>0.84。此时取yi=μi-1，则：

si=μi-1=dipi-1

综上则有：

(2)

以消耗弹药的总价值衡量费效比，总价值越低则越优。则目标函数为：

(3)

模型输出为yji，即i型弹药打击第j类目标时成功发射弹药量。由此可以计算总成功发射弹药量。

令Yj=(yj1,yj2,…,yjN),YT=(Y1,Y2,…,YL),C1×N=(c1,c2,…,cN),IN为N阶单位矩阵，b1×L=(1,1,…,1),s1×N=(s1,s2,…,sN)。A2和f为分块矩阵，均包含L个子块。

(4)

(5)

A2=(IN,…,IN)

(6)

f=(C1×N,…,C1×N)

(7)

将式(1)、式(2)、式(3)表示成线性规划模型的标准形式[5]：

(8)

通过Matlab线性规划函数[6]求解式(8)，则可得到经济成本最低的弹药使用分配方案Yj，目标函数值F为消耗弹药总价值。

2 应用示例

已知，某次作战行动需要打击A类目标10个，B类目标20个，C类目标30个，目标打击效果要求均为击毁。此次任务共有弹药4型，记为A、B、C、D，综合弹药毁伤能力、目标特性、战场环境，通过仿真分析得到每型弹药对相应目标打击的效能分析推荐量如表1所示。

表1 目标打击效能分析推荐量

各型弹药单价如表2所示。

表2 弹药单价 百万元

当前可用弹药数量及可成功发射概率如表3所示。

表3 弹药数量及发射成功率

代入式(8)求解得到经济成本最低的目标-弹药分配方案(需要成功发射的弹药数量)如表4所示，此时目标函数值达到最小为444，则对应的消耗弹药总价值达到最小为444百万元。该方案可确保84%以上的成功率。

表4 目标-弹药分配表

3 结论

文中基于整数线性规划模型构建了精确制导弹药的优化分配模型，该模型能够基于现有弹药数量、目标打击任务要求进行计算分析，给出经济成本最低的制导弹药使用分配方案，经过Matlab验证[6]。结果表明，该模型能够根据当前制导弹药数量和目标打击任务要求给出经济成本最低的制导弹药使用分配方案，提升了精确制导弹药使用分析的科学性。