精锻身管弹膛内壁成形圈纹缺陷机理研究

刘金明，刘兵，杨晨，任青松，樊黎霞

(1.南京理工大学 机械工程学院，江苏 南京 210094；2.重庆建设工业(集团)有限责任公司，重庆 400054)

0 引言

身管径向精锻是一个复杂的塑性成形过程，属于多次局部加载成形[1]，其特点有：多向同时锻打，有效限制金属横向流动，提高轴向的延伸效率；变形区处于三向压应力状态，金属塑性好；每次金属变形量小，变形速度快，变形力小；能提高锻件精度和降低表面粗糙度等[2]。身管弹膛通常由多个锥体组成，在锻打过程中常出现锥体凹处锻不透，靠近锥体凸处常出现材料起皱,以致肉眼都能看到很多环向圈纹，导致身管内表面成形质量差，达不到要求。如图1所示，其中红点区域为弹膛锻不透的部位，红线区域为产生环向圈纹的部位。陈玉雯等[3]和陈玉雯[4]研究发现，锻造过程中的径向应变改变量影响弹膛的锻透性，使用锻造段锻造比作为判断是否锻透的依据，解决了弹膛部位锻不透的问题。

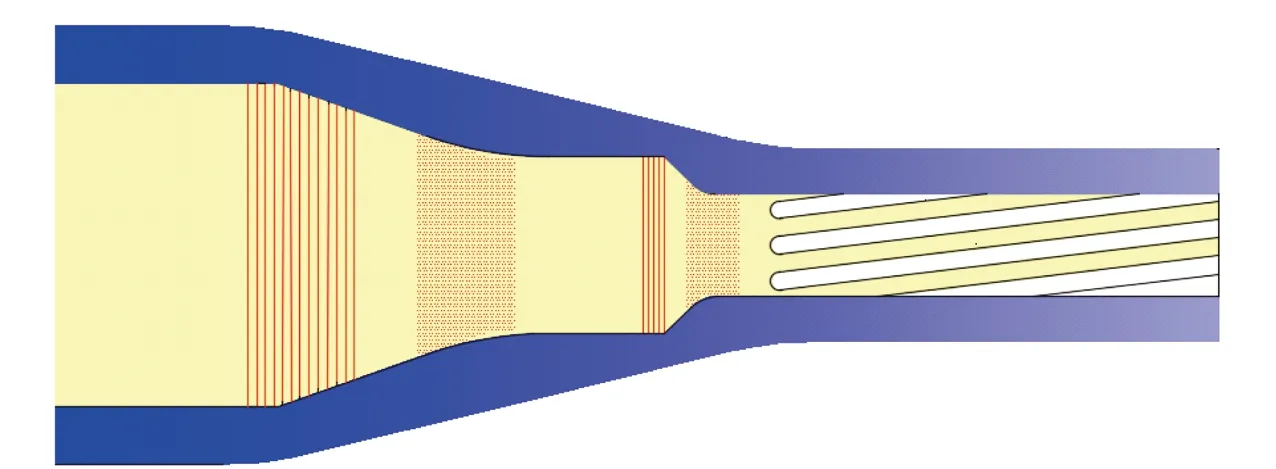
图1 弹膛精锻成形缺陷示意图Fig.1 Schematic diagram of forming defects of chamber during precision forging

对于身管线弹膛一体化的成形极限及问题，栾谦聪等[5]使用经验三角形法则分析了锻造工艺参数对锻透率的影响。樊黎霞等[6]研究了摩擦系数、轴向进给速度、锤头压入角及锻造比对锻打力的影响，讨论了不同工艺参数所对应的身管径向、轴向及周向内表面应力的分布情况；研究了身管精密锻造过程中的锻造比与塑性应变的关系，提出了内膛成形的必要条件[7]；使用数值仿真模拟了身管线膛内膛膛线的成形过程，分析了芯棒结构以及锻造比对膛线成形的影响[8]。张雪等[9]建立了以径向和周向塑性应变为表征的身管内膛膛线锻透的判断准则，得到以锻造比和毛坯径比为表征的身管锻透极限图。Ameli等[10]在研究冷径向锻造时，通过二维轴对称和三维有限元模拟研究了锻件中的残余应力，沟槽周围的应力，锤子和心轴上的压力分布以及最大锻造载荷。Ghaei等[11-12]运用主应力法研究了锤头的几何形状对径向锻造过程中工件成形的影响，还利用上限法建立了径向锻造过程中的应变方程，讨论了金属材料的轴向流动对材料应变的影响。Sanjari等[13-14]应用轴对称模型分析了管件径向锻造成形过程中各参数如摩擦系数、轴向进给率、尾端压力、前端拉力及锤头角度等对成形过程中的应变非均匀性的影响。Domblesky等[15]使用Abaqus有限元软件对径向锻造过程进行了数值模拟，研究了锻件进给速度和锻件不同点的等效塑性应变对其温度的影响。

本文以弹膛内壁圈纹问题作为研究对象，通过Abaqus有限元软件仿真对弹膛成形进行流动性分析、应力分析以及试验结果对比，研究弹膛内壁圈纹形成和消失的原因，并制定相关的判断准则。

1 身管精锻弹膛成形过程应力研究

身管的弹膛由数个有坡度的锥体组成，从身管尾端开始向右计数，分别为一锥、二锥、三锥、四锥等，锥体的数量及尺寸由子弹的形状决定。如图2所示，毛坯在锻造成形过程可分为下沉段、锻造段和整形段3个阶段。在下沉段毛坯内外径同时减小，但毛坯厚度保持不变；对于锻造段，毛坯与芯棒贴合，在锤头的锻打下厚度也不断减小；整形段时毛坯厚度不再变化。弹膛成形主要由锻造段决定。图2中，s为芯棒一锥结束点与锤头水平锻打面结束点之间的轴向距离。

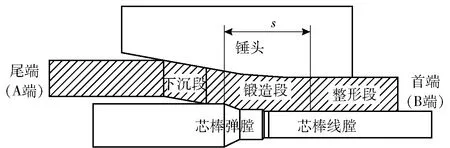
图2 身管精锻变形示意图Fig.2 Schematic diagram of deformation of forged barrel

身管弹线膛同锻过程可以分为线膛锻打阶段和弹膛锻打阶段两个阶段。锻打线膛时，芯棒相对锤头保持不动，毛坯尾端在夹头推动下，使毛坯首端与支承器紧贴并以同样速度轴向进给。因此，毛坯首端是位移约束、尾端是压力约束，锤头对毛坯进行周期性径向锻打，毛坯贴合芯棒线膛部分，内膛形成膛线。锻打弹膛时，芯棒与夹头接触，夹头A端轴向移动，毛坯首端支承器的轴向进给速度下降，芯棒与毛坯尾端速度相同，毛坯首端与支承器以匀速轴向进给。降压以后，毛坯尾端的夹持压强由p降到p1，毛坯尾端与夹头脱开，芯棒与夹头继续联在一起。当夹头无毛坯作用时，它与毛坯首端支承器的轴向速度相同。当弹膛基本成形后，锤头沿径向往外抬锤到一定位置，抬锤完成后锤头继续进行锻打直至结束。

1.1 身管精锻模型建立

根据弹线膛同锻的工艺过程,本文使用Abaqus有限元软件静态分析，对5.56 mm口径身管精锻过程进行模拟。为了节省计算量，将三维身管锻打模型简化为轴对称模型，忽略身管在锻造过程中的旋转动作。模型中含有芯棒、挡块、锤头、毛坯4个部件，其中锤头、挡块和芯棒在锻造过程中变形较小，设置为刚体；毛坯为主要变形件，设置为变形体。毛坯所使用的材料为30SiMn2MoV，该材料的本构模型为

σ=kεn，

(1)

式中：σ为等效应力；k为应变强化系数；ε为等效塑性应变；n为加工硬化指数。该材料的力学性能参数使用拉伸试验获取，如表1所示。

表1 毛坯材料力学性能参数Tab.1 Mechanical properties of blank material

身管毛坯设置的网格单元为4节点轴对称减缩积分单元(CAX4R)，在锻造过程中毛坯内壁与芯棒锥角接触的部位变形较大，因此对该部位进行网格细化，毛坯外侧则采用尺寸较大的网格，以提高仿真计算效率。锻打时毛坯与芯棒、锤头、挡块之间均有接触。考虑相互之间的摩擦，建立模型时定义3个接触对，即锤头与毛坯之间的接触、芯棒与毛坯之间的接触、挡块与毛坯之间的接触。摩擦类型选择为库伦摩擦模型，采用罚函数接触法定义各接触对之间的约束，滑移公式为有限滑移模式，表面粘结在一起时允许的最大滑移变形为单元长度的0.5%.毛坯与挡块间摩擦系数为0.15，与锤头间摩擦系数为0.25，与芯棒间摩擦系数为0.05.身管线弹膛锻打过程主要涉及进给速度、降压值和降压位置、抬锤量及抬锤位置等工艺参数。建立的有限元模型如图3所示。

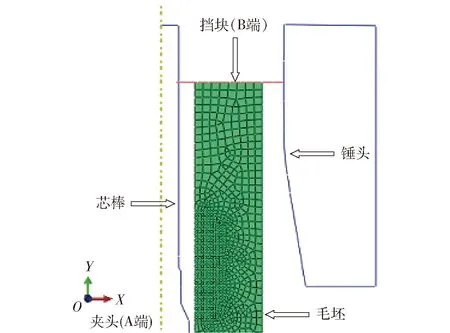
图3 身管精锻有限元模型Fig.3 Finite element model of barrel forging

1.2 身管弹膛成形过程

为了研究弹膛的成形过程中产生圈纹缺陷的机理，选取在成形特征点两侧的关键点进行分析。如图4所示，芯棒上A、B、C、D、E、F、G、H等8个关键点，A点位于芯棒线膛部位，B点和C点位于芯棒四锥的1/3部位，D和E点位于芯棒三锥上，F点和G点位于芯棒二锥的1/3部位，H点位于芯棒一锥上。图4中a、b、c、d、e、f、g、h等8个关键点为锻件内壁上的点，这些内壁节点在锻打完毕时，最终停留在芯棒弹膛的8个关键点处，位置分别与芯棒关键点一一对应。锻造的具体工艺参数如表2所示。

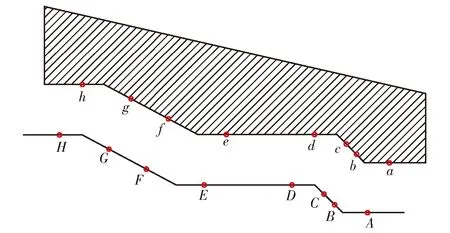
图4 芯棒弹膛关键点位置图Fig.4 Location of key points of mandrel cahmber

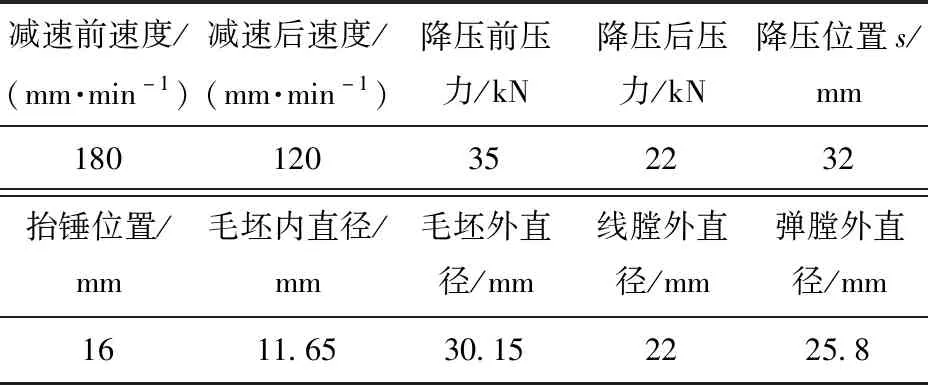
表2 身管锻造工艺参数Tab.2 Barrel forging process parameters

为了显示毛坯内侧材料与芯棒之间的接触以及相对流动状态，输出锻造过程中毛坯内壁节点和芯棒位置的坐标值，如图5所示。从图5中可以看出，毛坯内侧材料在锻造时沿芯棒向后移动，且后端的材料轴向流动距离大于前端材料，因此轴向上整体被拉长。其中d点和h点对应的毛坯内壁点在接触芯棒以后继续向后流动，穿过坡度较陡的四锥和二锥，最终停留在三锥和一锥上，跨越了锥段。因此，在研究身管弹膛内壁产生的缺陷时，需要考虑缺陷形成时毛坯与芯棒的相对位置，最终成形时内表面的圈纹缺陷是由前端流动过来的。

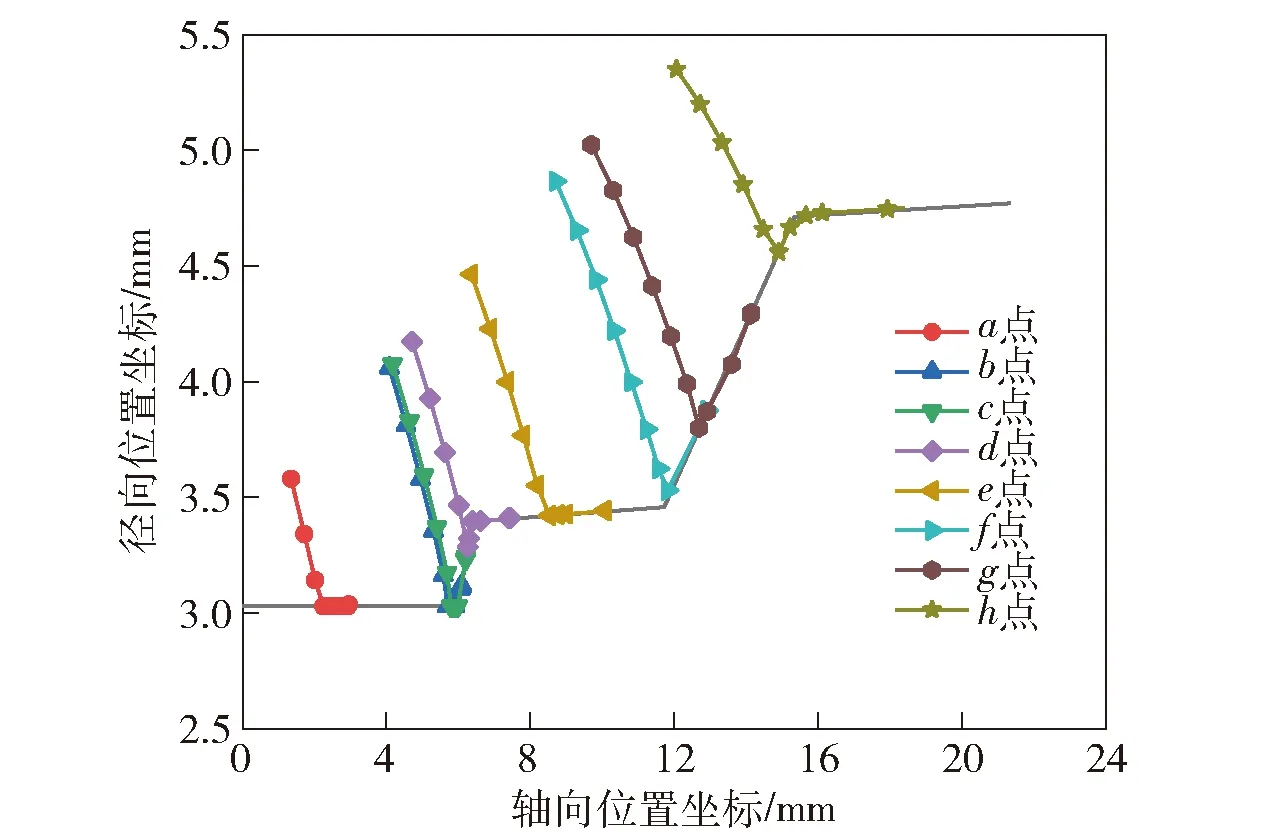
图5 弹膛内壁节点坐标变化图Fig.5 Change in node coordinate of chamber inner wall

1.3 锻打过程弹膛内表面切向应力分量变化

为了显示材料流动性的影响，分别采用拉格朗日法和欧拉法输出弹膛内表面切向应力分量。拉格朗日法是以研究单个质点运动过程为基础，综合所有质点的运动、构成整体运动的方法。欧拉法是描述众多质点流经一个空间点运动的方法。用拉格朗日法研究切向应力分量时，输出毛坯内壁关键点a、b、c、d、e、f、g、h在锻造过程中沿内表面的切向应力分量随锻打时间的变化。用欧拉法研究切向应力分量时，输出芯棒弹膛关键点A、B、C、D、E、F、G、H点对应的毛坯内壁节点在锻造过程中沿内表面的切向应力分量随锻打时间的变化。

仿真软件Abaqus输出的应力方向为径向和轴向，因此在输出内壁表面切向应力分量时，需要使用新旧坐标系的变换，将仿真软件输出的轴向和径向应力进行换算。旧坐标系下的应力分量矩阵为

(2)

式中：σr为径向应力；σz为轴向应力；σθ为周向应力；τrz、τrθ、τzr、τzθ、τθr、τθz为剪应力。由于身管的柱形特征，应力分量中周向剪应力分量均为0 MPa，即τzθ=τθz=0 MPa，τrθ=τθr=0 MPa.

新坐标、旧坐标系的单位基矢量分别用er′、ez′、eθ′和er、ez、eθ表示，新坐标系基矢量er′在旧坐标系3个坐标轴上的投影(与3个坐标轴之间的余弦)分别为lr、mr和nr，ez′的投影分别为lz、mz和nz，eθ′的投影分别为lθ、mθ和nθ.新旧坐标系的变换矩阵为

(3)

新坐标的应力分量矩阵可以表示为

σ′=TσTT.

(4)

经过计算，转换后得出的内壁切向应力分量为

(5)

身管弹膛主要包含4个锥段，计算切向应力分量时需要得知各锥段与身管中心轴之间的夹角，如表3所示，其中：二锥和四锥与中心轴之间的角度较大，沿内壁表面方向的切向应力分量同时受到轴向应力和径向应力的影响；一锥和三锥与中心轴之间的角度较小，切向应力分量主要受到轴向应力的影响，径向应力的影响可以忽略。

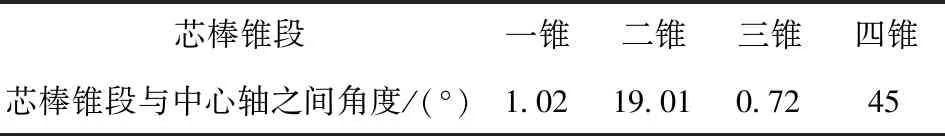
表3 芯棒锥段与中心轴之间夹角Tab.3 Angle between mandrel cone and central axis

取芯棒弹膛各锥段关键点处对应的毛坯内壁切向应力分量随时间的变化绘制图6,始终以位置点为观察对象,即以欧拉法输出切向应力分量。当毛坯材料没有接触到该点时,应力为0 MPa.从图6中可知，芯棒上各关键点位置不同，毛坯与芯棒各点接触时间也不同。毛坯内壁在与芯棒关键点接触以后，切向应力分量都为负值，表明毛坯内壁切向受压。关键点部位切向压应力在接触以后便迅速增大至峰值，这是因为毛坯沿芯棒向后流动的过程中受到芯棒锥角的阻挡，毛坯内壁与芯棒之间产生切向挤压。由于芯棒二锥和四锥坡度较陡，毛坯内壁与芯棒之间的挤压比其他部位更严重，位于芯棒二锥和四锥上的B、C、F、G点的切向压应力峰值远大于其他4个关键点。当各关键点进入整形段以后，内壁材料开始不再沿芯棒向后流动，毛坯与芯棒之间的切向挤压逐渐减小，各关键点的切向压应力开始减小至平稳。

图6 欧拉法输出切向应力分量变化曲线Fig.6 Output tangential stress component curves of Euler method

图7中以拉格朗日法输出切向应力分量，即锻件内壁a、b、c、d、e、f、g、h点在锻造过程中沿内壁表面方向的切向应力分量。这些关键点部位在未与芯棒接触时，切向应力分量不为0 MPa.b点、c点对应最终成形时的四锥部位，f、g点对应最终成形时的二锥部位。这4个关键点在流动过程中经过坡度较大的二锥与四锥，切向压应力峰值较大。与欧拉法不同的是，用拉格朗日法输出的切向应力分量体现了材料的流动性，图7中位于三锥和一锥的d、h关键点的切向压应力峰值也比较大，这是因为d、h关键点在锻造过程中与四锥和二锥先接触，产生较大的切向压应力，随后沿芯棒向后流动，跨越锥段停留在三锥和一锥上。锻件内壁上a、e关键点在整个锻造过程中没有与坡度陡的锥段接触，与芯棒之间没有产生较大的挤压，因此a、e关键点的切向压应力峰值比其他点小。

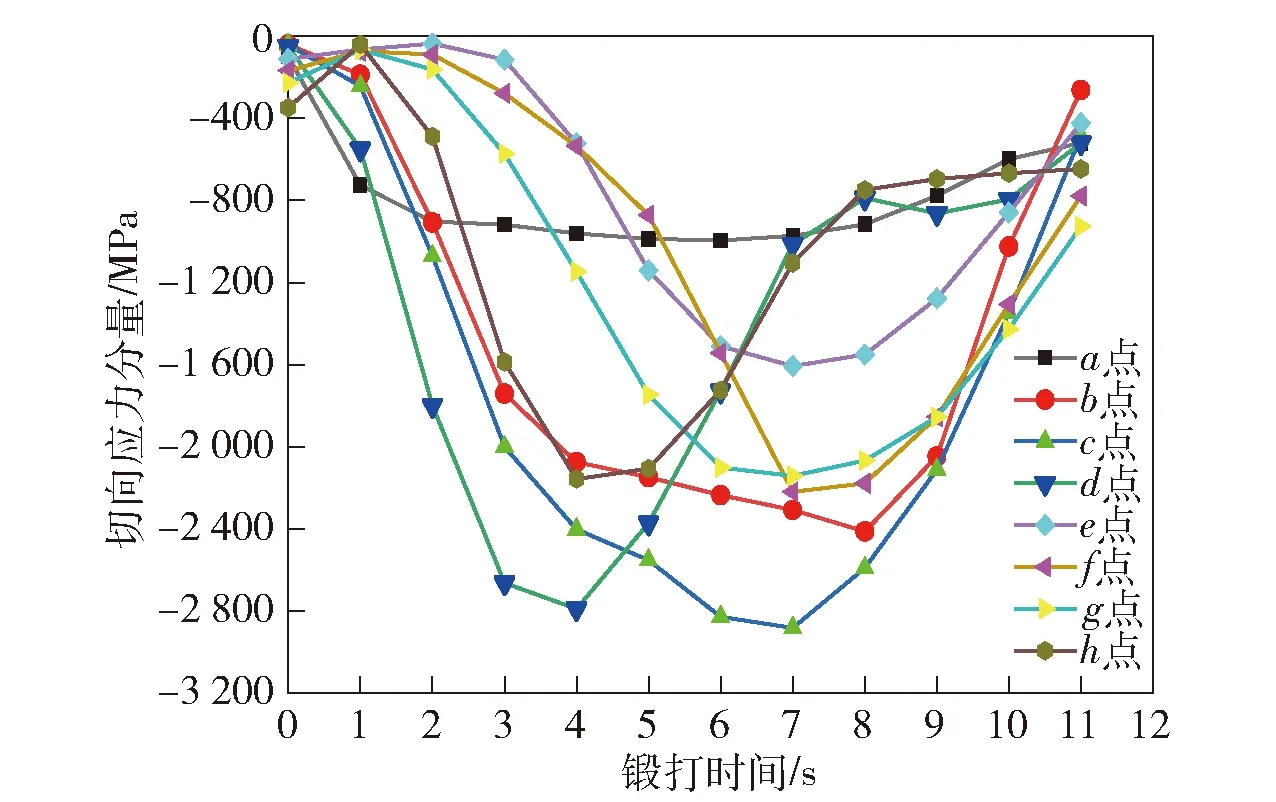
图7 拉格朗日法输出切向应力分量变化曲线Fig.7 Output tangential stress component curves of Lagrangian method

用欧拉法将芯棒各位置点在成形过程中的最大切向应力分量和芯棒位置关系绘制图8.由图8可以看出：弹膛二锥与四锥部位的切向压应力峰值远大于其他位置，四锥部位切向应力分量达到2 900 MPa，二锥部位达到2 300 MPa.从曲线中沿着线膛、四锥、三锥、二锥和一锥向右观察，线膛部位切向压应力峰值较小，临近四锥时开始逐渐增大，然后四锥部位保持平稳。四锥过后，三锥尾端部位的切向压应力峰值便陡然降低，然后临近坡度较陡的二锥，切向压应力峰值开始再次增大，二锥部位保持平稳。穿过二锥以后，一锥尾端的压应力峰值重新降低。

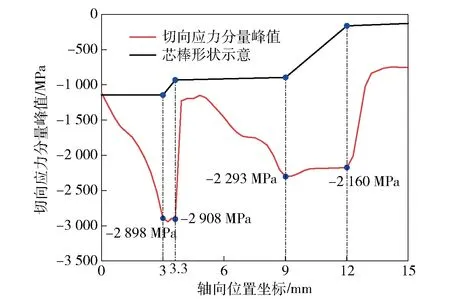
图8 弹膛切向压应力峰值曲线Fig.8 Shear tangential compressive stress peak curve

从以上现象可以发现，坡度较陡的锥段会增大毛坯与芯棒之间的挤压，导致毛坯内壁切向压应力增大，并且锥段越陡，切向压应力峰值越大。坡度较陡的锥段切向压应力峰值几乎不变，维持在一个稳定状态。陡锥对前面锥段的切向压应力峰值也有影响，距离陡锥越近，切向压应力峰值越大。

2 弹膛内壁圈纹机理研究和相关准则的建立

2.1 身管弹膛内壁失稳起皱机理的试验研究

将第1节分析的身管进行试验锻打，编号为2，与此同时,将其他参数身管也进行锻打，编号为1和3.锻打身管工艺参数见表4，其他工艺参数与表2相同。锻打结果如图9所示。

表4 身管编号及参数表Tab.3 Barrel number and parameters mm

图9 身管弹膛内壁成形图Fig.9 Forming of chamber inner wall

从图9所示锻打结果中发现，弹膛内壁二锥与三锥交接部位出现了锻不透的缺陷，锻不透在图中表现为表面粗糙度高、不光滑。其中1号试件比较严重，二锥大部分区域都未锻透，2号和3号试件也有部分区域未锻透。根据文献[3-4]的研究成果,弹膛二锥与三锥的交接部位处于凹陷状态，毛坯内壁材料难以充满该部位，身管弹膛部位锻不透的主要影响因素为锻造段锻造比，二锥和三锥连接部位锻透的锻造段锻造比阈值为23.8%.锻造段锻造比是指毛坯内表面触碰芯棒开始至成形结束时的截面积变化率，锻造段锻造比计算公式为

(6)

式中：Ab为毛坯接触芯棒时的截面积；Af为锻件截面积；ri为锻件内半径；hb为毛坯厚度；ro为锻件外半径。为了比较直观地解释弹膛部位锻不透的原因，将弹膛部位的锻造段锻造比与芯棒的位置坐标相结合，绘制弹膛锻造段锻造比变化曲线如图10所示。

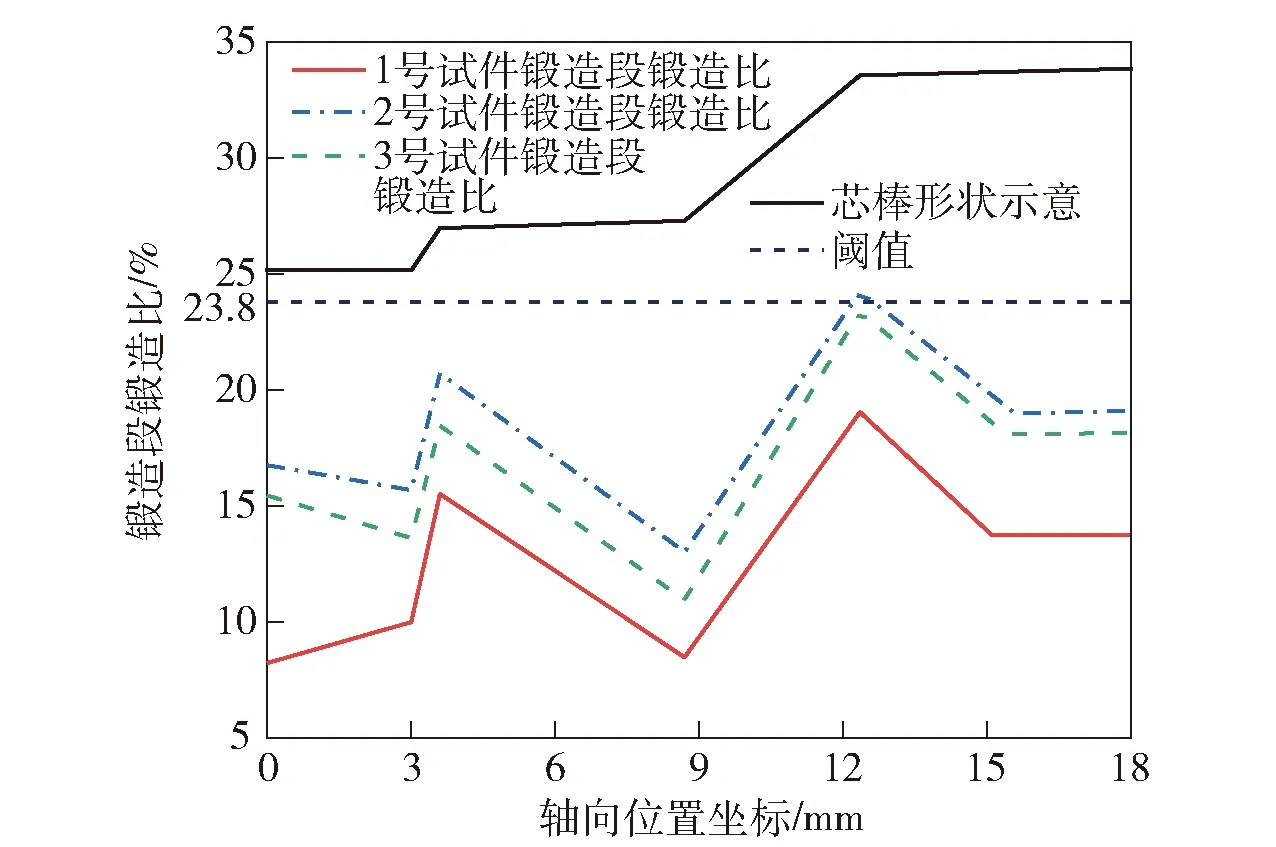
图10 弹膛锻造段锻造比变化曲线Fig.10 Changing curves of forging ratio of forging section of chamber

观察图10可知，从左向右，在二锥和四锥锥段，弹膛锻造段锻造比在逐渐上升，一锥和三锥锥段，锻造比在逐渐下降。这是因为二锥和四锥坡度较陡，横截面面积收缩严重，锻造段锻造比呈现上升的趋势。一锥和三锥相比其他锥段坡度比较平缓，但锤头不平，而是具有一定的倾斜角度，因此对一锥和三锥不同部位的径向锻打量不同，锻造段锻造比呈现下降的趋势。弹膛二锥与三锥交接部位的锻造段锻造比比其他部位小，这是因为该处处于凹陷状态，锤头对该部位的径向锻打量较小，毛坯内壁未完全贴合芯棒。一锥、二锥交接部位与三锥、四锥交接部位处于凸出状态，锤头的径向锻打量较大，锻造段锻造比也会更大。锻造过程中锤头需要抬锤，一锥部位的锻造比在减小以后逐渐趋于稳定。在整个弹膛部位，锻造比出现波浪形的变化趋势。1号、2号、3号试件的二锥、三锥交界处锻造段锻造比均小于锻透阈值23.8%，因此3根试件均出现不同程度的锻不透现象。

图9中弹膛部位的缺陷除了锻不透以外，一锥尾端、二锥和三锥尾端部位出现紧密排列的一圈圈环向纹路，纹路凹凸不平，严重影响了身管的成形质量。基于对弹膛内侧材料的应力和流动性分析，锻造过程中二锥和四锥出现的切向压应力峰值远大于弹膛其他部位，而出现圈纹的部位在锻造过程中会经过芯棒二锥和四锥。由此可以将锻件内壁产生圈纹的原因概括为：毛坯在锤头的径向锻打作用下沿轴向伸长，与芯棒贴合并往后流动，在流动的过程中与芯棒坡度较陡的二锥和四锥相互挤压，沿芯棒外表面产生较大的切向压应力。内壁材料在切向压应力较大的情况下发生失稳，致使材料凸出产生隆起，最终锻件弹膛部位出现一圈一圈的环向纹路。由此发现，锻件内侧材料在锻造过程中的切向应力值会直接影响到圈纹的产生，因此将材料的切向应力值作为弹膛内壁失稳起皱的影响因素，并通过试验来获取失稳起皱的阈值.当锻件内侧材料的切向压应力超过阈值时就会产生圈纹。

2.2 内壁失效起皱阈值讨论

为了获取圈纹的起皱切向压应力阈值，对上述3根身管进行有限元模拟分析，用欧拉法输出弹膛在锻造过程中的切向压应力峰值，如图11所示。从图11中可以看出,1号试件弹膛内壁四锥部位切向压应力达到2 400 MPa，2号试件四锥处达到2 900 MPa，3号试件四锥处达到3 400 MPa.实验结果显示二锥与四锥最容易失稳起皱产生圈纹，其中1号身管弹膛二锥部位有轻微失稳起皱现象，2号、3号身管弹膛三锥尾部和四锥出现较为严重的失稳现象，2号、3号身管弹膛二锥上有环向圈纹。结合实验现象和仿真结果，选取1号试件二锥处的切向应力分量峰值作为失稳的阈值，身管弹膛内壁发生失稳起皱的临界切向压应力a约为2 150 MPa，即超过该阈值弹膛内壁就会产生圈纹。

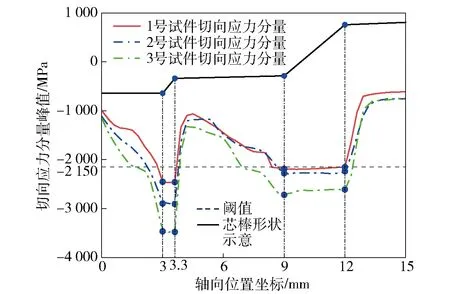
图11 弹膛切向应力分量峰值曲线Fig.11 Peak curves of shear tangential compressive stress components

2.3 身管弹膛内壁圈纹产生机理和消失进一步研究

在2.2节的研究中发现，最大切向应力分量往往产生在二锥或四锥上，因为这里比较陡，在通常的锻打中，切向应力分量都会大于失稳起皱的阈值，本文试验又锻打了2个成形试件4号、5号，其锻造工艺参数如表5所示，成形结果如图12所示。图12中显示两根身管弹膛都被锻透，内壁成形饱满、光滑。其中5号身管弹膛一锥尾端有轻微环向圈纹；4号身管弹膛内壁未出现任何缺陷，成形良好。其切向应力分量峰值在位置上的分布如图13所示。

表5 身管编号及参数表Tab.4 Barrel number and parameters mm

图12 身管弹膛内壁成形图Fig.12 Forming of chamber inner wall

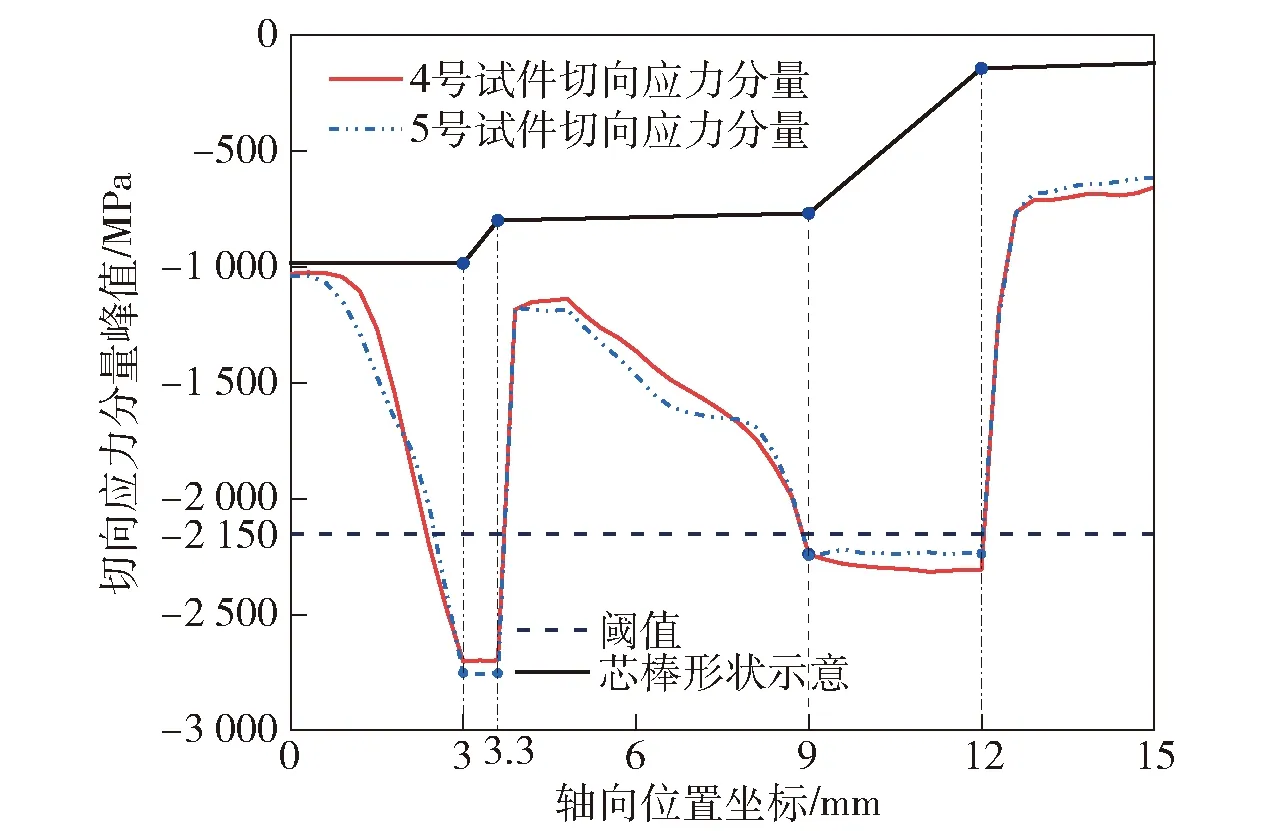
图13 弹膛切向应力分量峰值曲线Fig.13 Peak curves of shear tangential compressive stress components

从图13中发现：在锻打过程中，由于锻造工艺参数相近，4号和5号弹膛部位的切向压应力峰值相差不大；这两根试件弹膛二锥和四锥部位的切向应力分量峰值均超过了本文所设定的阈值。因此试件弹膛内壁会因切向压应力分量过大失稳起皱出现圈纹。但是从图12的成形结果中可以观察到，2根试件弹膛内壁成形良好，除5号一锥尾端有轻微圈纹之外，并未出现所预料的严重失稳起皱现象。

将上述5根试件弹膛部位的锻造段锻造比与芯棒位置坐标结合起来，绘制弹膛锻造段锻造比变化图如图14所示。从图14中发现，4号、5号试件二锥与三锥交界处的锻造段锻造比大于锻透阈值23.8%，即整个弹膛区域最难锻透的部位达到了锻透的条件，解释了这两根试件成形饱满的现象。对比4号、5号试件与上述1号、2号、3号试件，发现4号、5号试件弹膛部位的锻造段锻造比要远大于1号、2号、3号试件。由此得出结论：锤头锻打毛坯的锻造段锻造比会影响最终锻件内壁圈纹的产生，即锻造比越大，身管弹膛内壁越光滑，产生的圈纹越少。出现这种现象的原因为：锻造段锻造比越大，锤头对毛坯的径向下压量越大，毛坯受压导致内侧材料径向压应变也越大，锻造过程中由于挤压产生的圈纹又重新被压平，因此锻打完毕后锻件内表面没有出现圈纹。为获取圈纹被重新压平的锻造段锻造比临值，将上述4号、5号身管弹膛所有部位的锻造段锻造比与锻件内壁在锻造过程中的切向压应力峰值曲线结合起来，绘制锻造段锻造比与切向压应力峰值对应图如图15所示。

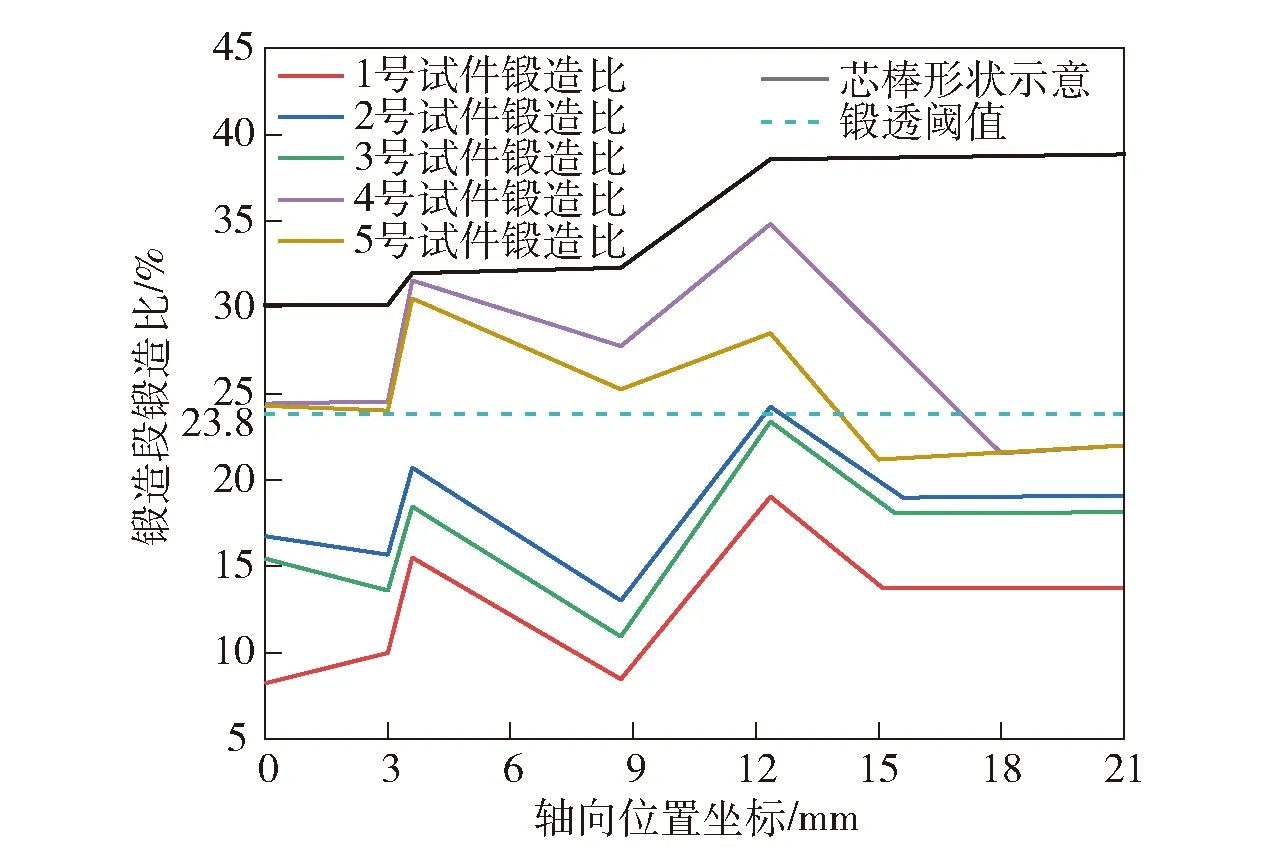
图14 弹膛锻造段锻造比变化图Fig.14 Change in forging ratio of forging section of chamber

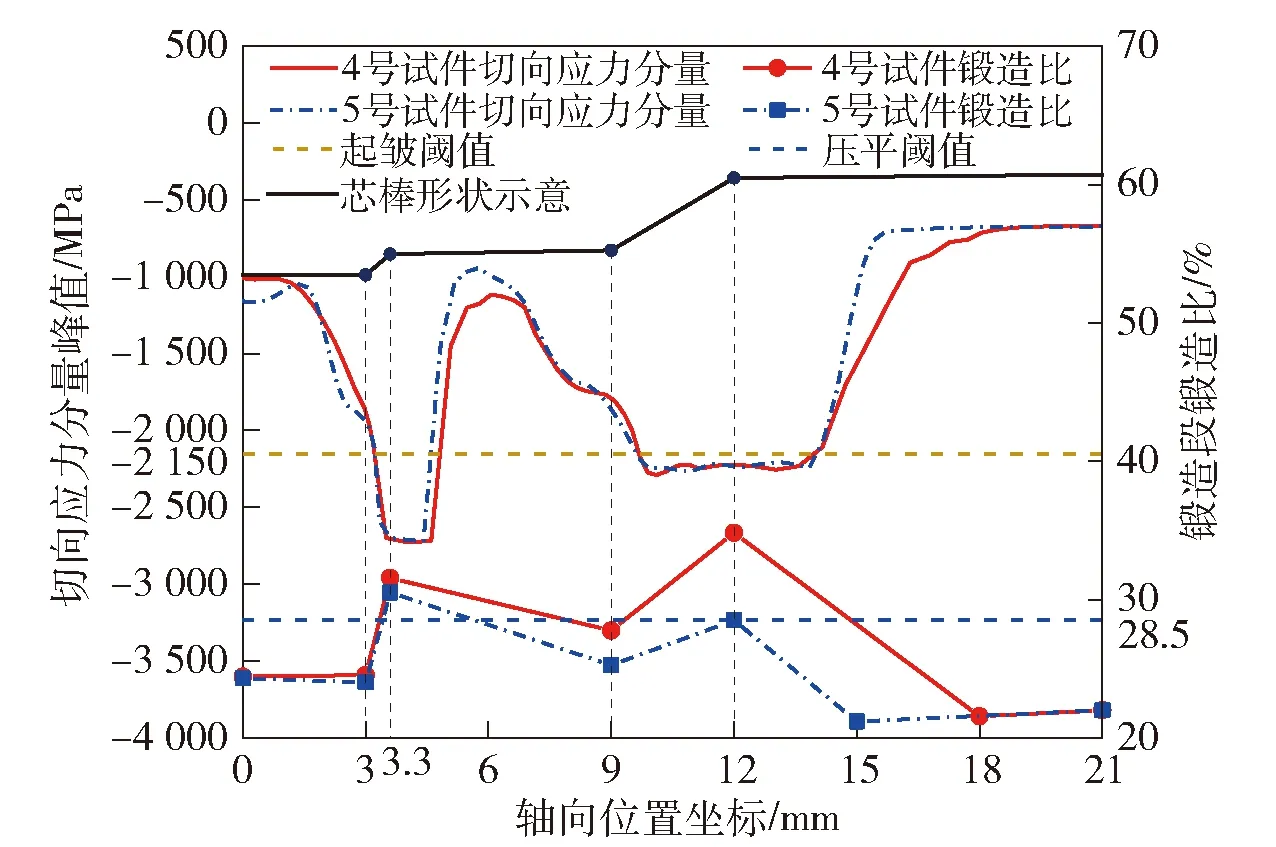
图15 锻造段锻造比与切向应力分量峰值对应图Fig.15 Forging ratio of forging section corresponding to peak of tangential compressive stress component

图15中的弹膛切向压应力峰值曲线用拉格朗日法输出，体现了毛坯内壁材料的流动性，内壁部分节点的切向压应力在接触二锥与四锥时达到峰值，随后沿芯棒表面流动，最终停留在一锥与三锥尾端，因此一锥与三锥尾端的峰值也相对较大。图15中棕色划线以下区域为4号、5号试件弹膛的切向压应力峰值超过起皱阈值2 150 MPa的部位，因为4号成形良好，5号一锥尾端有轻微的环向印记，所以选择5号试件一锥与二锥连接点处的锻造段锻造比作为临界值。4号试件超过起皱阈值区域的锻造段锻造比均达到压平圈纹的临界值，因此弹膛内壁未产生圈纹。由此可以获取压平圈纹的锻造比阈值，大约为28.5%.

3 结论

1)身管弹膛内壁环向圈纹的产生与材料受压失稳有关，弹膛内壁在锻造过程中的切向压应力超过临界值即出现失稳起皱现象。有限元分析结果表明，芯棒二锥和四锥由于坡度较陡，在锻造过程中阻碍毛坯内侧材料往后流动，导致毛坯内壁产生了较大的切向压应力，增大了该部位出现失稳的可能性。结合试验结果，弹膛内侧材料失稳起皱的切向压应力阈值大约为2 150 MPa.

2)弹膛内壁产生的圈纹可能会在后续锻打过程中被压平，主要影响因素为锻造段锻造比。锻造段锻造比越大，锤头对毛坯的径向锻打量越多，圈纹越可能被压平，压平圈纹的锻造段锻造比阈值大约为28.5%.

3)身管弹膛部位的主要成形缺陷为锻不透和起皱产生圈纹，综合满足锻透和压平圈纹的条件，弹膛凹陷部位的锻造段锻造比应大于23.8%，凸出部位的锻造段锻造比应大于28.5%.