类比寻方法 整合提素养——多面体外接球半经的求法探究

广东顺德罗定邦中学

求多面体的外接球半经问题,是近年高考的热点和难点之一,已有不少文章对其进行了探究,本文从多边形的外接圆圆心、半径的确定类比到多面体的外接球球心、半径的确定,并且由球心的确定方法将各类多面体的外接球题型进行了分类.

一、补成长方体,求其对角线长即得球直径

类比矩形内接于圆,直径就是矩形的对角线.长方体内接于球,这是因为长方体的四条体对角线长相等,交于一点且互相平分,这点就是球心,体对角线就是球的直径(图1).长方体可以切割为墙角锥(共顶点的三条棱两两互相垂直(如图2),或底面是长方体的一个面的四棱锥);阳马(不共点的三条棱两两互相垂直(如图3),或有不同方向的三条两两互相垂直棱可以作为长、宽、高的三棱柱、四棱锥等);对棱体(对棱相等的四面体,如图4).

图1

图2

图3

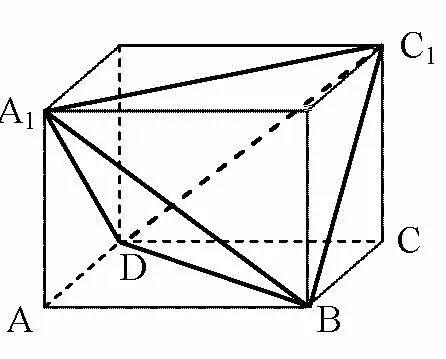
图4

这些多面体可补成长方体,长方体8个顶点所在的球面就是这些多面体的顶点所在的球面,其外接球就是长方体的外接球,直径就长方体的体对角线.要求这些多面体的外接球直径,只要求出它们所在长方体的体对角线长即可.我们把这种方法称为补体法.

例1一个四面体的所有棱长都为四个顶点在同一球面上,求此球的表面积.

解四面体所有棱长相等,则对棱相等,可补成一个长方体,设长,宽,高为x,y,z,则x2+y2=2;x2+z2=2;y2+z2=2; 如上三式求和得,外接球直径R满足(2R)2=x2+y2+z2=3,所以S表=4πR2=3π.

二、已知某个侧面的外心及该面上的高时确定外接球的方法

类比多边形的外心在各边的中垂线上,多面体的外接球的球心在经过各面外心的垂线上.

多面体的面截球所得的截面圆就是该面多边形的外接圆,我们熟知直角三角形的外心是斜边的中点; 矩形的外心是两对角线的交点; 正三角形的外心是中心;另一特别的三角形,即顶角是120°等腰ΔABC,其外接圆半径r=腰长a,底BC的弦心

图5

(一)高是垂径

顶点在底面的射影是外心时,一个平面截球面,所得的截面是一个圆面,球心在截面圆的垂径上.设截面圆半径r,球半径R,面心距OO1=d,则有勾股关系:R2=r2+d2.由此可求球半径.

图6

图7

例1′(例1的另一解法) 如图7,正四面体任意面均可作为截面,其外接圆心O1是截面正三角形的中心,半径三侧棱相等,顶点A在截面的射影是O1,高由R2=(h-d)2=d2+r2,求得距所以S表=4πR2=3π.

(二)高是弦

顶点在底面的射影在球面上时,设AB是截面圆O1的直径,球面上一点P,PA⊥截面圆O1,则PB的中点O是球心,这是因为OO1//PA,所以OO1⊥截面圆O1,O到截面圆上每一点的距离相等,由OB=OP,所以O是球心,PB为直径,PB2=PA2+AB2,即(2R)2=(弦高)2+(2r)2.

图8

图9

例2在四面体S-ABC中,SA⊥平面ABC,∠BAC=120°,SA=AC=2,AB=1,则该四面体的外接球的表面积为( )

√解析如图9,ΔABC所在截面圆直径AE=2r=球心O在过截面圆心O1的垂线OO1,连结SE,则中点O就是球心,因为OO1⊥截面ABC,OE=OS=答案选D.

(三)任意高

设球面上一点P在截面圆O1上的射影为H,称HO1为足心距,设PH=h,则PH//OO1,球心O到P点的距离等于O到截面圆上任一点的距离(如图10),即:

由此先求面心距OO1=d,再求球半径.

图10

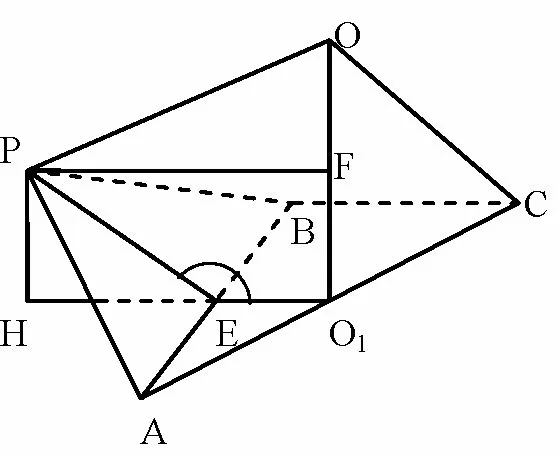
图11

例3已知在三棱锥P - ABC中,AB⊥BC,AB=且二面角P -AB-C的大小为150°,则三棱锥P-ABC外接球的表面积为____.

A.100πB.108πC.110πD.111π

解析如图11,ΔABC为直角三角形,知外心O1是AC中点,半径球心为O,OO1⊥面ABC,只要求出高PH和足心距HO1即可,设AB中点为E,PE⊥AB,O1E⊥AB,∠PEO1是二面角P - AB - C的平面角,∠PEO1=150°,设P在面ABC的射影为H,则由(*) 得到:解得选D.

例4四面体ABCD中,∠ADB=∠BDC=∠CDA=60°,AD=BD=3,CD=2,则四面体外接球的半径为____.

解析如图12,ΔDAB是正三角形,知外心O1是中心,半径只要求出高DH和足心距HO1即可.设AB中点为E,连DE、CE,则平面CDE⊥平面ABD,C点在面DAB上射影H在DE上,O1也在DE上,由cos ∠CDA=cos ∠HAD×cos ∠CDH得所以,得d=0,底面DAB恰好是大圆,所求球半径

图12

例5(2018佛山一模) 如图13,平面四边形ABCD中,沿直线AC将ΔACD翻折成ΔACD′,当三棱锥D′ -ABC的体积取得最大值时,该三棱锥的外接球的表面积为.

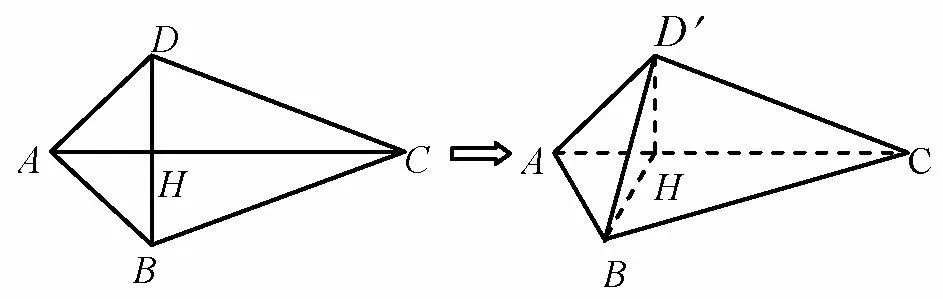
图13

图14

解析四边形是筝形,如图,BD⊥AC,当面ACD′⊥面ABC时体积最大,此时ΔABC面上的高DH确定.由余弦定理求得高DH=BH=1,只要确定底面ΔABC的外心、半径和足心距即可.在底面ΔABC的实际图中(如图14),由正弦定理设AC中点为E,弦心距O1E2=r2- CE2=1,所以足心距O1H2=HE2+O1E2=2,所以由(*) 式有得d=1,R2=r2+d2=6,所求球表面积为24π.

三、已知两面外心,定球心求球半径

类比圆心是两弦的中垂线的交点,则球心O是两截面圆的垂径的交点(如图15),这是因为OO1是截面圆O1的垂径,OO2是截面圆O2的垂径.设公共弦的中点为E,则O1E,O2E都垂直于公共弦,∠O1EO2是两截面所成二面角的平面角,在四边形OO1EO2中,只要求出OO1,OO2中的一个,结合已知截面圆半径,均可求出球半径.

图15

例6三棱锥P -ABC中,ΔABC是边长为3的等边三角形,D是线段AB的中点,DE ∩PB=E,DE⊥AB,若求三棱锥的外接球的半径.

解析因为AB2=PA2+PB2,所以ΔPAB是直角三角形,截面圆心是斜边AB中点D,ΔABC是正三角形,截面圆心是该三角形的中心O1,半径球心是两截面的垂径的交点O,由∠EDC=

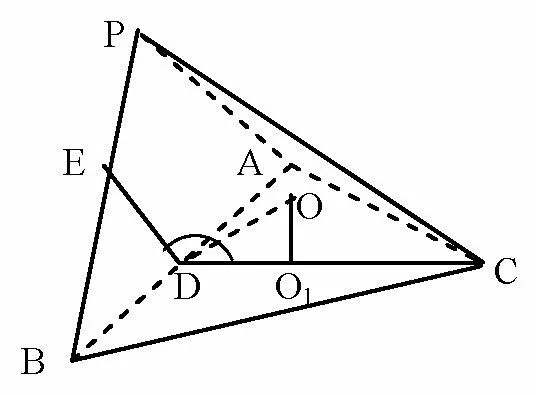
图16

例7在三棱锥S-ABC中,SB⊥BC,SA⊥AC,SA=AC,SB=BC,AB边长是SC一半,且三棱锥S-ABC的体积为则该三棱锥的外接球半径为( )

A.1 B.2 C.3 D.4

解析ΔSBC是等腰直角三角形,其截面圆心是斜边SC的中点;ΔSAC是等腰直角三角形,其截面圆心也是斜边SC的中点,所以SC中点O是球心.连OA,OB,则OA,OB都垂直SC,所以R=3,选C.

图17

解析ΔABD是顶角为120°的等腰三角形,外接圆半径r1=2,弦心距同理,ΔACD的外接圆半径r2=2,弦心距因为面ABD⊥面ACD,所以∠O1EO2=90°,两截面的弦心距与圆心垂线组成矩形,表面积为28π.

图18

四、灵活运用

多面体的外接球问题,上面给出了三种思维方向,如何选择？如何形成程序化解题步骤？首先,判断此多面体能否补成长方体(是否有三方向棱两两垂直或对棱相等),如能,问题解决;如不能,则有哪些面能确定外心并算出外接圆半径及该面上的高?然后确定是由两面的垂径定球心算半径,还是由一个面及该面的高算球半径,完成题解.

例9(2019年高考全国Ⅰ卷理科第12题) 已知三棱锥P -ABC的四个顶点在球O的球面上,PA=PB=PC,ΔABC是边长为2的正三角形,E,F分别是PA,AB的中点,∠CEF=90°,则球O的体积为( )

解析1如图19,由PA=PB=PC,P在底面内的射影是ΔABC的外心O1,所以球心O在PO1上,只要求出PO1即可,设PC=a,在ΔPAC中,用余弦定理求得由已知∠CEF=90°,即EF2+EC2=FC2,得:所以由(*) 式 求 得答案选D.

图19

解析2由已知∠CEF=90°,期望找到相互垂直的三棱,通过补形法求直径,可得PB//EF,所以PB⊥EC,又易证PB⊥AC,所以PB⊥平面PAC,进而可证PA,PB,PC两两垂直,计算得PA2+PB2+PC2=6.余下同解析1.

例10(2019顺德一模) 已知四棱锥P -ABCD的五个顶点在球O的球面上,ABCD为正方形,且AB=2,PA=则球O的体积为( )

例8已知三棱锥A-BCD中,AD=BD=CD=2,∠BDA=∠CDA=120°,面ABD⊥面ACD,则三棱锥A-BCD的外接球表面积为____.

解析1正方形ABCD的外心是中心O1,因为AB2=PA2+PB2,ΔAPB是直角三角形,其外心O2是AB中点,由PC2=BC2+PB2,得BC⊥PB,又PD2=PA2+AD2,得AD⊥PA,BC//AD,所以BC⊥PA,PB ∩PA=P,故BC⊥平面PAB,进而面PAB⊥面ABCD,所以两面垂径的公共点是正方形ABCD的中心O1,即为球心,答案选B.

解析2如图20,由ΔAPB是直角三角形,BC垂直面PAB,所以PA,PB,BC两两垂直,则该几何体可补成一个以PA、PB为长、宽,BC为高的长方体,(2R)2=PA2+PB2+BC2=

图20

解析3底面半径在底面的射影H在BA上,高由(*) 算得d=0,半径

五、结束语

解决多面体的外接球问题,充分体现了数学核心素养(数学抽象、直观想象、逻辑推理、数学运算、数学模型等),而掌握基本数学思想方法是提升学生数学核心素养的基本途径.