基于标记增强的多标记代价敏感特征选择算法

黄锦涛，钱文彬，2，王映龙

1(江西农业大学 计算机与信息工程学院，南昌 330045)2(江西农业大学 软件学院，南昌 330045)

1 引 言

在机器学习中，每个示例只属于一个类别标记，该类问题被称为单标记学习.但由于在现实生活中，随着数据规模和维度急剧增长，数据的内容越来越复杂，其包含的语义信息日益丰富，使得每个示例往往同时含有多个类别标记，在真实世界中多标记高维数据广泛存在.近年来，多标记学习引起国内外诸多学者的广泛关注和研究，且成功应用于文本分类[1，2]、图像识别[3，4]，情感分析[5]及语音识别[6]等领域.

多标记学习旨在回答“哪些标记可以描述该样本？”，即现有的多标记学习中标记是以逻辑均匀分布的形式描述.然而，在许多应用领域中每个标记对于示例的描述程度往往不同.例如，在图像识别领域，一幅山水画可能被标记为“山、水、蓝天”等多个标记，然而这些标记在这幅画中所占的比例是不同的.因此，每个实例的相关标记的重要度往往不同，这些标记的重要程度构成该示例的标记分布，即示例含有的标记以概率分布形式描述.标记分布学习(Label- distribution learning)作为一种新的机器学习方法[7-10]，在许多现实问题中具有较好的普适性，诸多学者已对其展开相应研究.例如：Zhou等人[11]针对情感分析中，每种表情与多种情绪相关联的情况，通过所提出的情绪标记分布学习方法来学习每个基本情绪的具体描述度.Xu等人[12]通过标记分布解决了半监督下的标记缺失问题，利用迹范数最小化的标记相关性提出了一种近端梯度下降算法.Zhao等人[13]为了分析标记的相关性，利用传输理论和标记分布下的距离度量公式，提出了一种基于最优化传输理论的标记分布学习新方法.

与单标记学习一样，多标记学习也面临着数据的高维性问题.特征选择，又称属性约简，通过删除不相关或冗余特征有效实现数据降维，以减少算法的训练时间和增强学习算法的分类性能.例如，Lin等人[14]使用模糊互信息构造特征重要性度量准则，基于此设计了一种有效的多标记特征选择算法.Liu等人[15]提出了一个在线多标记属性约简算法，该算法包括在线组属性约简和在线组间属性约简两个阶段.He等人[16]提出了一个多标记学习框架，该框架综合分析了多标记学习中的多标记分类，标记相关性，标记缺失和多标记特征选择问题.另外，在现实生活中特征数据的获取往往需付出成本代价.基于代价敏感的特征选择问题已引起了研究者的关注，并取得了一些有意义的成果.在多标记学习中，Teisseyre等人[17]提出了一种将特征代价纳入学习过程的算法，并将分类器链和惩罚逻辑回归相结合应用于多标记属性约简及分类.Wu等人[18]通过探索多标记学习中复杂的输入关系，将正负标记间的相关性嵌入基于代价敏感的多标记学习.在上述的研究中，尤其是在多标记学习中，均假定不同标记对于同一示例而言，其重要程度是等同的.然而，在实际应用中，多标记高维数据中每个示例的相关标记重要度往往不同.因此，从代价敏感学习的视角，研究基于标记增强的的多标记特征选择具有重要的意义.

为此，本文针对基于标记增强的多标记高维数据，从代价敏感学习的视角，提出了一种基于特征依赖度和特征代价相结合的特征选择算法.首先，本文基于邻域粗糙集与随机变量分布，提出了一种可将传统多标记数据中标记的逻辑分布增强为标记分布的标记增强方法.然后，在标记增强后的标记分布数据中，从代价敏感学习视角，将特征代价与特征依赖度进行线性融合，构建了一种新的特征重要性度量准则，并以此设计了面向标记分布数据的代价敏感特征选择算法.最后，为了验证算法的有效性和可行性，本文选取了Mulan六个真实多标记数据集，通过三种不同的代价分布函数生成特征代价；实验结果表明，本文通过标记增强分析了每个示例的相关标记重要性，可有效选择出低总代价的特征子集，同时能保持较优的分类性能，为多标记特征选择提供了一种可借鉴的方法.

2 基本知识

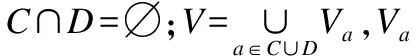
定义 1.在决策表DT=(U,C∪D,V,f)中，给定任意特征子集B⊆(C∪D),设IND(B)={(x,y)∈U×U|∀a∈B,f(x,a)=f(y,a)}为一个二元不可区分关系IND(B).U/IND(B)表示为论域U的一个划分，简记为U/B，其中U/B的任意元素[x]B={x,y|∀a∈B,f(x,a)=f(y,a)}称为等价类.

定义 2.在决策表DT=(U,C∪D,V,f)中，∀R⊆(C∪D),X⊆U,则X关于R的上近似集和下近似集可表示为：

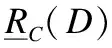
对于多标记学习而言，决策特征为一组标记集合.结合粒计算理论，多标记数据可定义为五元组多标记决策表MDT=(U,C∪L,V,f)，其中L={l1,l2,…,lm}为m个标记集合.U,C,V,f和上述定义相同.

3 多标记学习下的标记增强

由于现有多标记学习的研究通常假定每个示例的相关标记的重要度相同，然而在许多现实应用领域，对于每个示例而言，其所拥有的标记的重要程度往往不同.为此，本节基于邻域粗糙集与随机变量分布，提出了一种面向多标记数据的标记增强方法，该方法可将传统多标记数据中标记的逻辑分布增强为标记分布数据，使其分类算法在训练过程中能获得更多的监督信息.

定义 3.对于多标记决策表MDT=(U,C∪L,V,f)，设特征子集B⊆(C∪L)，特征子集B上的邻域粒度表示为：

δB(xi)={x|x∈U,Δ(x,xi)≤δ}

其中δ为邻域粒度的阈值大小.Δ(x,xi)为x与xi间的距离度量公式.距离度量公式可采用曼哈顿距离、欧式距离或切比雪夫距离公式.阈值δ计算可由如下公式获取：

其中θ为调节参数，其范围为[0.1，2.0].

定义 4.对于多标记决策表MDT=(U,C∪L,V,f)，给定任意实例xi∈U,任意标记lj∈L，对于实例xi，每个标记lj的重要度表示如下：

对于∀1≤i≤n,∀1≤j≤m，有：

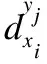
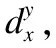
LDT=(U,C∪Y,V,f)

其中，Y={y1,y2,…,ym}为增强后的标记集合.

表1 多标记决策表
Tabel 1 Multi-label decision table

Uδ(xi)l1l2l3l4x1δ(x1)={x1,x3,x4}1010x2δ(x2)={x2,x4,x5}1011x3δ(x3)={x1,x3,x4}1100x4δ(x4)={x1,x2,x3,x4}1111x5δ(x5)={x2,x5}0111

实例分析：为进一步详细说明标记增强的过程，以表1为例进行分析，邻域计算时采用欧式距离.根据定义4可计算增强后的各个标记.

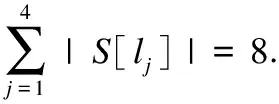
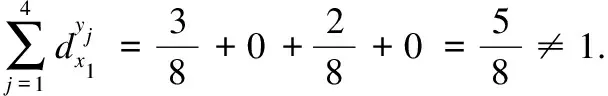
同理，可计算出其余示例的各个相关标记的概率分布.增强后的标记分布决策表如表2所示.

表2 标记分布决策表
Table 2 Label distribution decision table

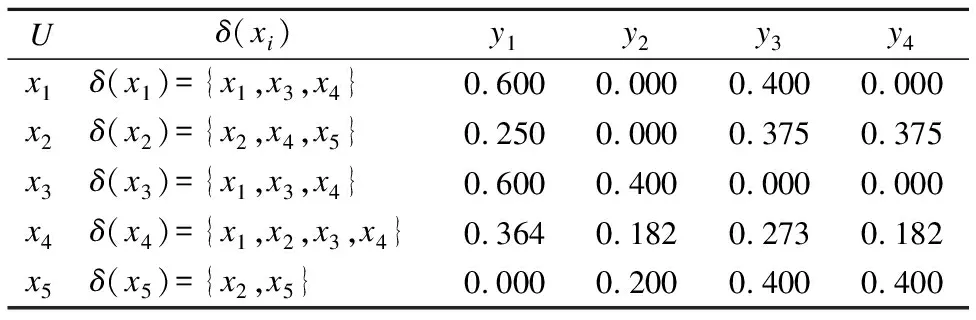
Uδ(xi)y1y2y3y4x1δ(x1)={x1,x3,x4}0.6000.0000.4000.000x2δ(x2)={x2,x4,x5}0.2500.0000.3750.375x3δ(x3)={x1,x3,x4}0.6000.4000.0000.000x4δ(x4)={x1,x2,x3,x4}0.3640.1820.2730.182x5δ(x5)={x2,x5}0.0000.2000.4000.400

4 标记增强下的多标记代价敏感特征选择

由于在现实生活中，多标记数据的规模和维度急剧增长，数据的内容越来越复杂.多标记高维数据中所包含的类别标记信息日益丰富.特征选择作为一种特征降维技术，可以有效解决高维数据带来的维度灾难问题.同时，特征数据的获取亦需要付出成本代价，使得代价敏感学习问题广泛存在于实际应用中.因此，研究标记增强后的多标记代价敏感特征选择具有现实的意义.

定义 6. 给定标记分布决策表LDT=(U,C∪Y,V,f)，对于任意对象x∈U，任意特征子集B⊆C，任意标记y⊆Y，特征子集B下实例x的等价类为[x]B，在标记集合Y下实例x的邻域为δY(x). 标记分布下的上下近似集可表示为：

定义 7.在标记分布决策表LDT=(U,C∪Y,V,f)中，给定任意特征子集B⊆C，标记分布下特征子集B关于Y的正区域表示为：

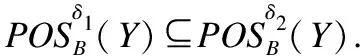
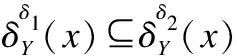
定义 8.在标记分布决策表LDT=(U,C∪Y,V,f)中，对于任意特征子集B⊆C，标记分布下特征子集B的特征依赖度为:

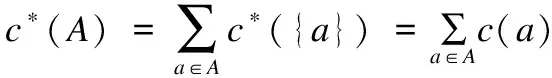
LCDT=(U,C∪Y,V,f,c)

定义10.给定标记分布代价敏感决策表LCDT=(U,C∪Y,V,f,c)，对于任意特征子集B⊆C，其特征重要性度量公式可表示为:

对于任意特征a∈C-B, 其相对于特征子集B的重要度可表示为：

性质 2.在标记分布代价敏感决策表LCDT=(U,C∪Y,V,f,c)中，对于任意特征子集B⊆C,∀b∈B,如果特征b是必要的，则有:

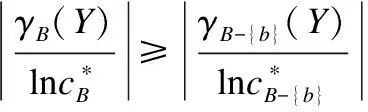
由上述分析可知，针对标记增强后的多标记代价敏感特征选择，首先通过计算每个示例在条件特征集下的等价类，并根据标记的邻域阈值计算标记集合下每个示例的邻域粒度，基于此，可计算出条件特征集下的正域集合.然后，根据定义10利用启发式搜索策略，首先分别计算每个特征的正域示例个数，基于此进一步计算当前特征的重要度.依次比较每个特征重要度的大小，将重要度最大的特征加入候选特征子集，直至候选特征子集的正域示例与整个条件特征集下的正域示例集合相同.根据上述过程，设计了一种标记增强后的多标记代价敏感特征选择算法.如算法1所示.

算法1.基于标记增强的多标记代价敏感特征选择算法

输入：标记分布代价敏感决策表LCDT=(U,C∪Y,V,f,c)，标记邻域阈值δ

输出：特征子集R

Begin:

Step 1.初始化R=∅；

Step 2.for(i=1;i≤|U|;i++):

计算特征集下每个样本xi的等价类[xi]C；

计算标记集合下每个样本xi的邻域δY(xi)；

endfor

Step 3. 根据定义8，计算全集特征下的正域POSB(Y)；

Step 4.for(j=1;j≤|C|;j++)

Step 4.1.对于特征aj∈C-R,计算R∪aj下的等价类[xi]R∪aj；

Step 4.2.计算特征aj的正区域POSaj(Y)及其特征重要度SIG(aj,R,Y)；

Step 4.3.如果POSR∪aj(Y)=POSC(Y)，则Step 5，否则执行Step 4.4；

Step 4.4.如果对于特征aj，满足aj=argmax {SIG(aj,R,Y)}，则将aj加入特征子集R， 即R=R∪aj.

endfor

Step 5.返回特征选择子集R

End

算法复杂度分析：对于Step 2，需计算每个示例在整个条件特征集下的的等价类及标记集合下的邻域粒度，其时间复杂度为O(|C||U|2+|Y||U|2)；对于Step 3，该步骤只需计算整个条件特征集下所有对象的正域，其时间复杂度为O(|U|)；算法Step 4利用启发式搜索策略进行特征子集的选择，其最坏时间复杂度为O(|C||R||U|2+|R||U|).由于大多数情况下，标记集|Y|远小于条件特征集|C|，综上分析，该算法的时间复杂度为O(|C||R||U|2).

5 实验与结果分析

5.1 实验设置

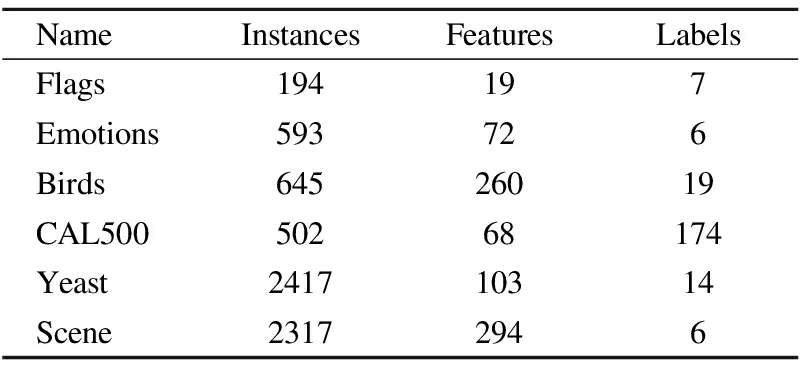
为了验证本文算法的有效性和可行性，首先选取了Mulan数据库中的6个真实多标记数据集进行验证和分析，其分别为Flags，Emotions，Birds，Yeast，CAL500，Scene.对于邻域阈值，本文实验选择欧式距离度量公式.六个数据集的邻域阈值分别为：Flags：0.2980，Emotions：0.2547，Birds：0.2140，CAL500：0.1542，Yeast：0.1698，Scene：0.2130.6个数据集的详细信息如表3所示.

本实验的运行环境：CPU为Inter(R)Core(TM)i5-4590s(3.0GHz)，内存为16.0 GB.所使用的编程语言为Python和Java，所使用的开发工具为PyCharm及Eclipse.然后，与当前四个主流的多标记特征选择算法进行实验对比和结果分析，其分别为MDDMspc[20]，MDDMproj[20]，RF-ML[21]，PMU[22].在MDDMspc和MDDMproj算法中，参数u=0.5；RF-ML算法中k-近邻个数k=5；PMU算法中离散化值为4类.

表3 多标记数据集
Table 3 Multi-label data sets

NameInstancesFeaturesLabelsFlags194197Emotions593726Birds64526019CAL50050268174Yeast241710314Scene23172946

为了验证本文提出的基于标记增强的多标记代价敏感特征选择算法的有效性，本实验将使用三种不同的分布函数来生成特征代价：均匀分布，高斯正态分布以及帕累托分布.其中，三种分布的M和N取值为10和30.三种分布函数描述如下：

1)均匀分布(Uniform Distribution)：该分布在构造特征的代价矩阵中使用最为广泛，均匀分布是一个概率分布.其代价构造方程如下：

Ct(M,N,x)=M+(N-M+1)x

2)高斯正态分布(Normal Distribution)：该分布在均值周围聚类，倾向于使用概率密度函数来描述变量.本文使用标准的正态分布构造代价方程：

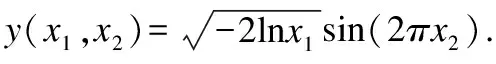
3)帕累托分布(Pareto Distribution)：它是一种有力的概率分布，可用于描述科学和精算等.而现实生活中有界Pareto分布则更实用.有界帕累托分布定义如下：

通过该有界帕累托分布，可获取特征代价构造方程：

Ct(M,N,x)=|p(M,N,x)|

5.2 评价指标

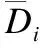
1)Rate of cost-reduction(RCR)：它评估了特征子集B的代价占全特征集C总代价的比率：

其中RCR值越小，代价约简效果越好.

2)Hamming Loss(HL)：它评估实例中预测标记与真实标记间的平均差异值：

其中⊕表示为异或运算，HL越小，分类性能越好.

3)One Error(OE)：它评估了标记排名靠前的实例不在实际实例中所占的比率：

其中One Error值越小，分类性能越好.

4)Coverage(CV)：它评估了全部实例中实际包含所有类别标记需要的最大排序距离：

其中rank(di)为标记di的排序；Coverage的值越小，分类性能越好.

5)Ranking Loss(RL)：它评估了标记中实际不包含的标记比实际不包含的标记排序高的比率：

其中k为任一实例与每个标记的之间的似然值；Ranking Loss值越小，分类性能越好.

6)Average Precison：它评估了在所有标记的预测集合中，排在相关标记之前的标记仍是相关标记的比率：

其中Average Precison值越大，分类性能越好.

5.3 结果分析与比较

为了验证本文所提算法的有效性，我们选取了四种不同的多标记特征选择算法进行实验对比和分析，其分别为MDDMspc[20]，MDDMproj[20]，RF-ML[21]，PMU[22]，并采用10倍交叉验证法对算法进行验证.这四种算法均为特征排序算法，本文算法为确定的特征子集算法.因此，实验的对比和分析将以本文算法选择的特征子集中的特征个数为准.六个数据集最终所选取的特征子集中特征的个数分别为：Flags：8个，Emotions：5个，CAL500：5个，Birds：7个，Yeast：6个，Scene：8个.实验结果如表4所示，其中斜体加粗表示当前数据集的最优值.(↓)表明当前评价指标取值越小，效果越优.(↑)表明当前指标取值越大，效果越优.

由表4～表6的代价约简率可知，本文所提算法所选择的特征子集通过三种代价函数所生成的特征总代价，在六个数据集上明显小于其他算法.表4中对于Birds数据集，MDDMproj，MDDMspc，PMU，RF-ML这四个算法所选择的特征子集的总代价分别是本文算法的4.09，5.41，2.61，6.20倍.如表5中对于 Emotions数据集，MDDMproj，MDDMspc，PMU，RF-ML这四个算法所选择的特征子集的总代价分别是本文算法的2.73，2.4，2.6，2.4倍.

综合六个数据集，本文算法对比其他四个算法的平均代价约简率，在均匀分布上分别降低了5.33%，11.63%，10.97%，12.40%，在正态分布上分别降低了4.17%，13.33%，12.68%，12.01%，在帕累托分布上分别降低了4.01%，9.55%，10.27%，10.09%.由此可知，本文算法在特征选择过程中将每个示例中相关标记的差异性及特征代价同时考虑，能有效降低选取特征子集所耗费的代价.

表4 均匀分布下五种算法的代价约简率(↓)
Table 4 RCR of five compared algorithms based on
uniform distribution(↓)

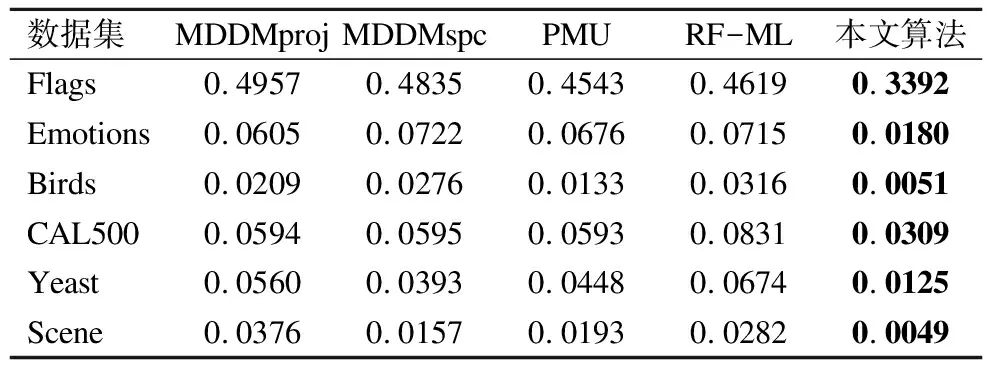
数据集MDDMprojMDDMspcPMURF-ML本文算法Flags0.49570.48350.45430.46190.3392Emotions0.06050.07220.06760.07150.0180Birds0.02090.02760.01330.03160.0051CAL5000.05940.05950.05930.08310.0309Yeast0.05600.03930.04480.06740.0125Scene0.03760.01570.01930.02820.0049

表5 正态分布下五种算法的代价约简率(↓)
Table 5 RCR of five compared algorithms based on
normal distribution(↓)

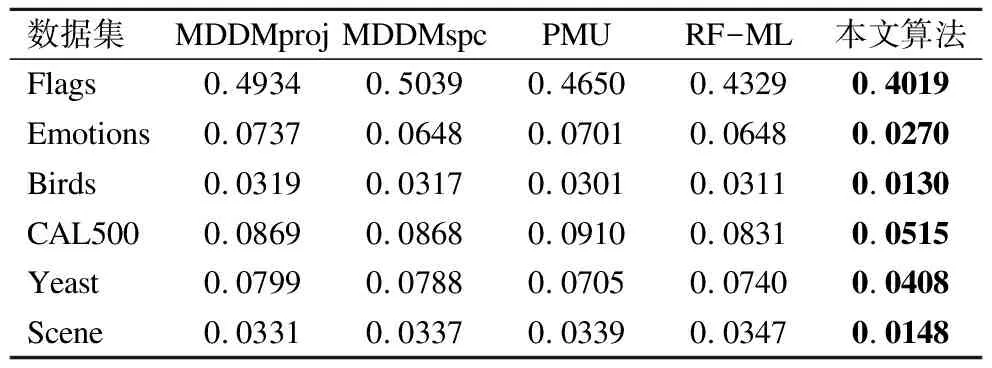
数据集MDDMprojMDDMspcPMURF-ML本文算法Flags0.49340.50390.46500.43290.4019Emotions0.07370.06480.07010.06480.0270Birds0.03190.03170.03010.03110.0130CAL5000.08690.08680.09100.08310.0515Yeast0.07990.07880.07050.07400.0408Scene0.03310.03370.03390.03470.0148

表6 帕累托分布下五种算法的代价约简率(↓)
Table 6 RCR of five compared algorithms based on
pareto distribution(↓)

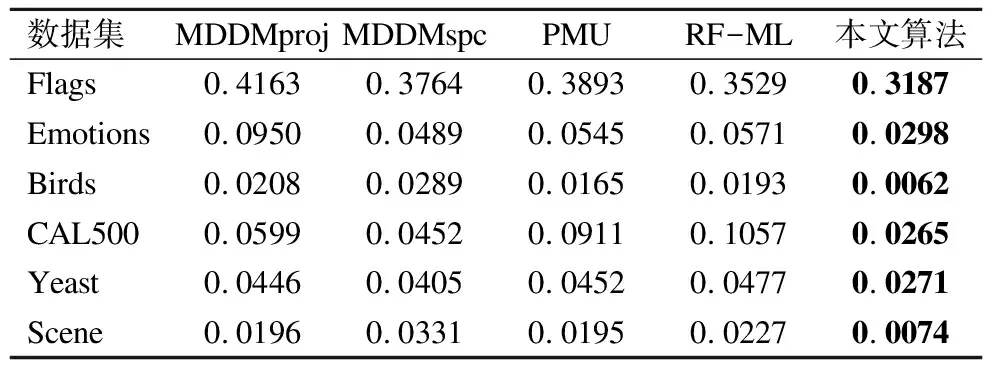
数据集MDDMprojMDDMspcPMURF-ML本文算法Flags0.41630.37640.38930.35290.3187Emotions0.09500.04890.05450.05710.0298Birds0.02080.02890.01650.01930.0062CAL5000.05990.04520.09110.10570.0265Yeast0.04460.04050.04520.04770.0271Scene0.01960.03310.01950.02270.0074

表7～表11展示了在标准正态分布下，五种算法在六个数据集上的五项分类性能指标.其中斜体字表明在当前数据集上的分类性能最优值.

表7 五种算法下的汉明损失(↓)
Table 7 Hamming Loss(↓)of five compared algorithms

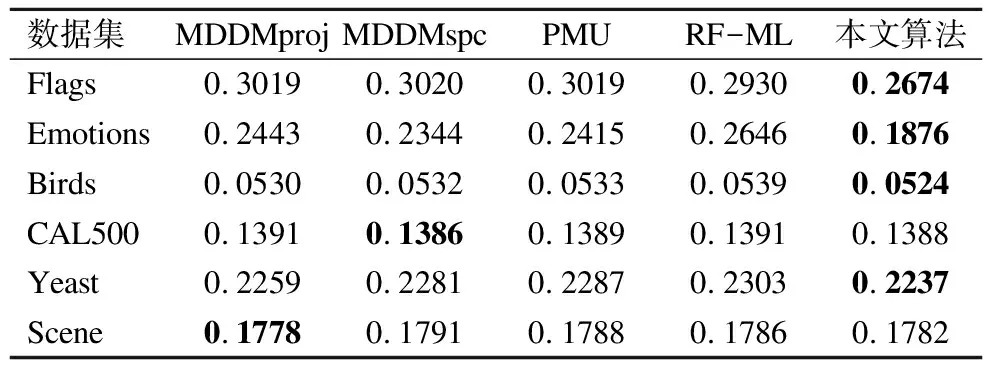
数据集MDDMprojMDDMspcPMURF-ML本文算法Flags0.30190.30200.30190.29300.2674Emotions0.24430.23440.24150.26460.1876Birds0.05300.05320.05330.05390.0524CAL5000.13910.13860.13890.13910.1388Yeast0.22590.22810.22870.23030.2237Scene0.17780.17910.17880.17860.1782

由表7结果可知，针对Hamming Loss，本文算法在四个数据集上均优于其他算法.在CAL500数据集及Scene数据集上，本文算法接近当前其他算法的最优值.特别地，在Emotions数据集上，本文算法要优于MDDMproj，MDDMspc，PMU和RF-ML算法，分别降低了5.67%，4.68%，5.39%，7.70%.此外，在其他数据集上，本文算法的Hamming Loss明显低于其他算法，这主要是因为在Hamming Loss中，需考虑预测标记与真实标记间的差异.即本文算法考虑了多标记数据中每个示例中相关标记重要度的不同，能有效减少标记预测时的损失.

表8 五种算法下的1错误率(↓)
Table 8 One error(↓)of five compared algorithms

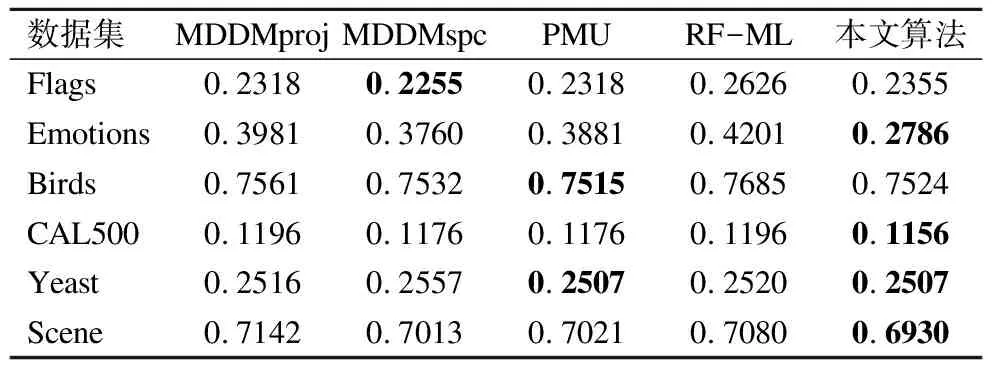
数据集MDDMprojMDDMspcPMURF-ML本文算法Flags0.23180.22550.23180.26260.2355Emotions0.39810.37600.38810.42010.2786Birds0.75610.75320.75150.76850.7524CAL5000.11960.11760.11760.11960.1156Yeast0.25160.25570.25070.25200.2507Scene0.71420.70130.70210.70800.6930

由表8中One Error实验结果可知，本文算法在四个数据集上均优于其他算法.其中，PMU算法在Birds和Yeast数据集上指标较好，该算法主要考虑了特征与标记之间的互信息来选取有效的特征子集，而本文算法在Yeast数据集上同样优于其他算法.但由表5可知，PMU算法在Yeast数据集上所耗费的特征代价是本文算法的1.73倍，由此可知，本文算法所选择的特征子集特征代价相对较小，且能保持较优的分类指标.

表9 五种算法下的覆盖率(↓)
Table 9 Coverage(↓)of five compared algorithms

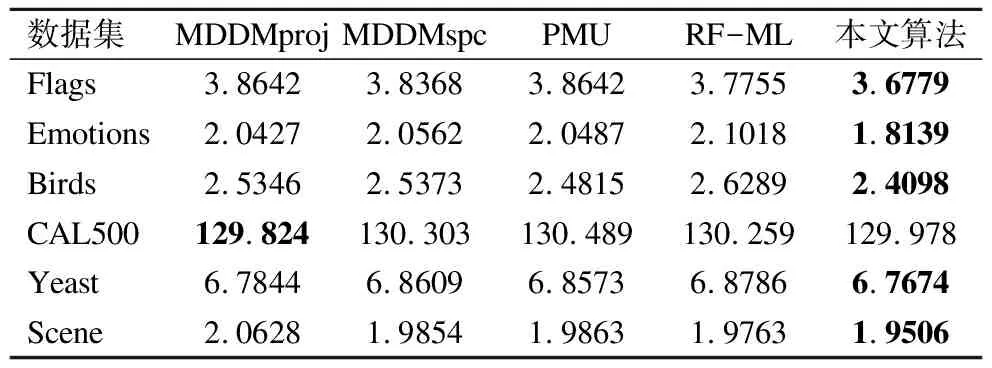
数据集MDDMprojMDDMspcPMURF-ML本文算法Flags3.86423.83683.86423.77553.6779Emotions2.04272.05622.04872.10181.8139Birds2.53462.53732.48152.62892.4098CAL500129.824130.303130.489130.259129.978Yeast6.78446.86096.85736.87866.7674Scene2.06281.98541.98631.97631.9506

针对表9中Coverage分类指标，本文算法在五个数据集上明显优于其他算法.特别地，在Yeast数据集上，与MDDMproj、MDDMspc、PMU和RF-ML算法相比，本文算法分别降低了1.7%，9.35%，8.99%，11.12%，同时，在代价约简率上本文算法分别降低了3.91%，3.80%，2.97%，3.32%.在Scene数据集上，本文算法相比于其他四个算法其分类指标分别降低了11.22%，3.48%，3.57%，2.57%，代价约简率分别降低了1.83%，1.89%，1.91%，1.99%.由此可见，本文算法在中大型数据集上分类效果表现优越.

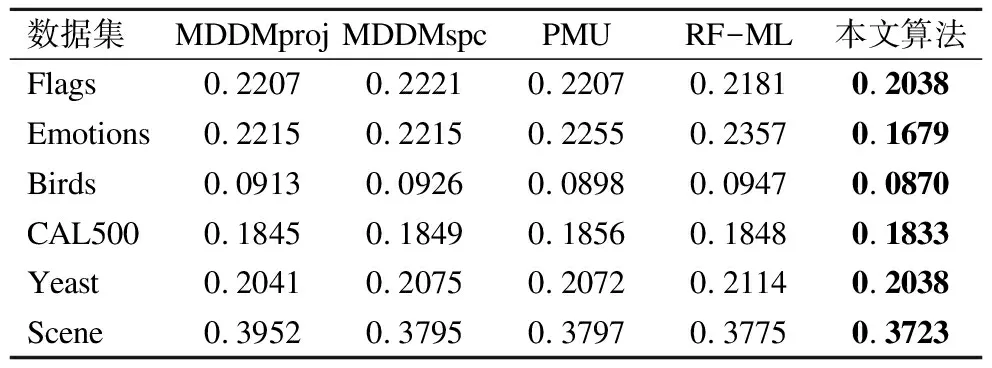
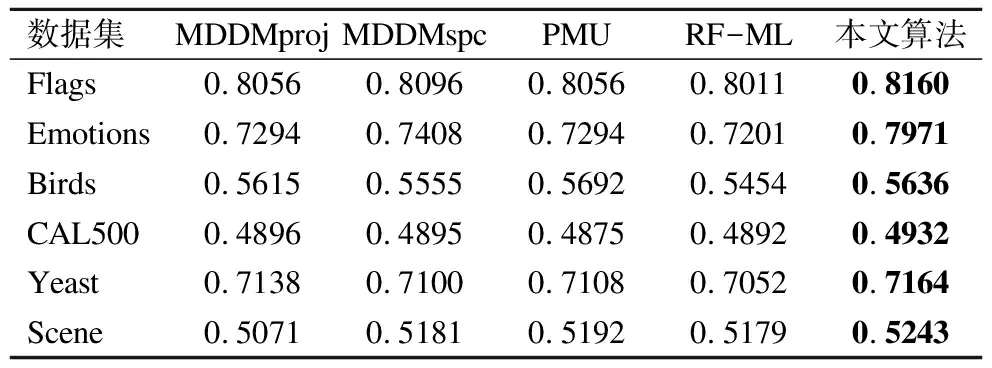
由表10和表11可知，本文算法在六个数据集上Ranking Loss和Average Precision的分类指标均优于其他四个算法.特别在Emotions数据集上，本文算法对比于MDDMproj，MDDMspc，PMU和RF-ML，Ranking Loss的值分别降低了5.36%，5.36%，5.76%，6.78%，而Average Precision的值提高了6.77%，5.63%，6.77%，7.70%.同时，在代价约简率上，本文算法对于与其他四个算法，分别降低了4.67%，3.78%，4.31%，3.78%.综合分析比较这六个数据集，本文算法在Ranking Loss上的与其他算法的平均排序分别相差2，2.75，2.58，2.67.在Average Precision上，平均排序分别相差2.17，2，2.17，3.67.由于Ranking Loss及Average Precision均需考虑标记排序所带来的的影响，而本文算法中利用标记增强方法将将多标记数据中传统的逻辑标记转化为监督信息更丰富的标记分布数据，能更加有效的减少标记排序所带来的损失，从而提高分类精度.

表10 五种算法下的排序损失(↓)
Table 10 Ranking Loss of five compared algorithms

数据集MDDMprojMDDMspcPMURF-ML本文算法Flags0.22070.22210.22070.21810.2038Emotions0.22150.22150.22550.23570.1679Birds0.09130.09260.08980.09470.0870CAL5000.18450.18490.18560.18480.1833Yeast0.20410.20750.20720.21140.2038Scene0.39520.37950.37970.37750.3723

表11 五种算法下的平均精度(↑)
Table 11 Average Precision of five compared algorithms(↑)

数据集MDDMprojMDDMspcPMURF-ML本文算法Flags0.80560.80960.80560.80110.8160Emotions0.72940.74080.72940.72010.7971Birds0.56150.55550.56920.54540.5636CAL5000.48960.48950.48750.48920.4932Yeast0.71380.71000.71080.70520.7164Scene0.50710.51810.51920.51790.5243

由表4～表6代价约简率可知，本文算法在保持分类性能相对较优的情况下，能选择出低总代价的特征子集.由表7～表11可知，本文算法在五项分类性能指标上总体优于其他四种算法，在Coverage，Ranking Loss以及Average Precision等指标上表现更好.本文所提算法在Emotions和Yeast两个数据集上五项分类指标优于其他算法，在Flags，Birds及Scene三个数据上分别有四项分类指标优于其他四个算法.综上所述，在多标记代价敏感特征选择的过程中，通过标记增强及考虑特征代价，能有效选取总代价较低的特征子集，并能保持较优的分类性能.

6 结束语

传统多标记学习中假定每个示例所拥有的不同标记的重要程度是相同的.然而，在现实生活中，多标记学习每个示例中不同标记的重要度往往不尽相同.因此，本文将标记分布学习引入代价敏感学习，利用标记增强方法将多标记数据转化为标记分布数据，并采用均匀分布，高斯正态分布和帕累托分布三种分布函数生成每个特征的代价，然后在特征代价和特征依赖度的基础上提出一种新的特征重要性度量准则，基于该准则构造了特征选择算法.通过对六个真实数据集的分析和比较，并与四种不同的多标记特征选择算法进行实验对比，实验结果验证了本文算法的有效性和可行性.未来工作中我们将进一步考虑从误分类代价视角研究标记分布特征选择问题.