一种新型高效的无参数化聚类算法
2020-04-11陈靖飒程开丰吴怀岗
陈靖飒,程开丰,吴怀岗
1(南京师范大学 计算机科学与技术学院,南京 210023)2(南京大学 电子科学与工程学院,南京 210023)
1 引 言
K-means算法是一种非常经典的无监督聚类算法,由于该算法具有原理简单、易于描述、时间效率高且适于处理大规模数据等优点[1],因此被广泛地应用于众多领域.但该算法也存在明显的缺陷:聚类的准确度和计算复杂度严重依赖于初始聚类数k和初始簇中心参数的选择.而在大量实际应用场景中,数据集不仅规模大,而且一直处于动态变化过程中,所以聚类数和聚类中心往往是很难提前预知和确定的.
为了解决上述问题,学者们相继提出了一些改进方案:文献[2]提出了利用迭代最大距离法来选取初始簇中心,它的基本假设是距离最远的样本点最不可能被分到同一个簇中,所以为了确定初始簇中心,迭代地选择样本集中距离最远的样本,直至样本数达到要求,该类算法虽然能解决传统K-means算法初始簇中心选择的问题,但由于每次迭代时都要计算所有非簇中心集中样本与簇中心集中样本间距离的乘积并再比较排序,计算复杂度太高,而且最后选取出的初始簇中心会分布在样本集的边缘,会导致K-means的收敛速度变慢.文献[3]提出了基于最小生成树的MSTCluster聚类算法,该算法首先将数据集抽象成赋权完全图WCG模型,其中的点代表向量,赋权边代表数据间的相似关系;然后将WCG转换成全连通的最小生成树MST,接着统计最小生成树中边集权重的均值μ和方差σ,然后将μ+λ*σ作为阈值PT对最小生成树进行剪枝.实际聚类效果证明该方法在很多场景能够取得很不错的聚类效果,而且计算复杂度相对经典K-means有了明显优化,但问题是剪枝阈值中的调节因子 的取值目前还没有统一的标准,实际使用时还是得依靠经验设置.文献[4,5]在最小生成树聚类算法和层次聚类算法的基础上,提出了一种通过控制参数来改变目标函数,进而在目标函数最小时得到最优聚类结果的算法,该类算法输入参数少且能够识别任意形状任意密度的簇,但依旧是需要人为确定参数的,且目标函数的收敛性难以证明,即如果目标函数不收敛则得不到最佳聚类结果.文献[6]提出了一种基于最小生成树的自适应阈值自顶向下分层聚类算法,该算法先根据最近邻关系划分最小生成树的边集,再统计当前最小生成树边集的均值和方差,进而根据一个控制参数ρ按照一定的计算方式得出阈值,可以看出该算法也是需要人为设置参数值的,而不是完全自适应的.文献[7]提出了一种改进的最小生成树自适应空间点聚类算法,该算法根据最小生成树边长的数理统计特征定义裁剪因子,进而通过宏观和局部两轮剪枝逐步打断最小生成树中的长边,从而得到最终聚类结果,该算法的自适应程度较高,但裁剪因子中仍含有需要人为确定的参数,也不是完全自适应的.
综上可见,虽然已经有很多学者尝试从不同角度去解决K-means算法对经验参数的依赖性和计算复杂度高等问题,并取得了一定进展,但仍有改进的空间.
2 MNC算法
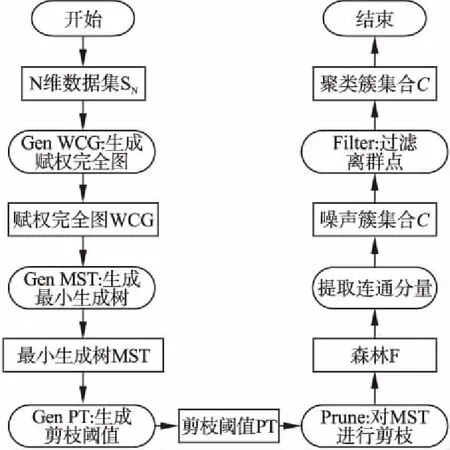
本文在前述工作的基础上提出了一种基于最小生成树的无参数化聚类算法MNC(MST based Non-parameterized Clustering),该方法先利用最小生成树理论[8]将待聚类的数据集转换成最小生成树;然后利用k=2的经典K-means算法将最小生成树边集的一维权重空间进行聚类,得到两个权重集合W1和W2,再根据Everitt 在1974 年关于聚类所下的定义“一个类簇是测试空间中点的会聚,同一类簇的任意两个点间的距离小于不同类簇的任意两个点间的距离”[9]得到,max(W1) MNC算法的基本流程如图1. MNC总体可分成5个阶段,分别为:生成赋权完全图、生成最小生成树、生成剪枝阈值、剪枝分裂和离群点过滤.每个阶段分别由相应的子函数GenWCG、GenMST、GenPT、Prune和Filter来实现,具体每个阶段的子函数实现细节如下. 首先将SN中的每个数据样本看成N维欧式空间的向量,数据样本间的相似度用向量间的欧氏距离来度量,则原数据样本集可以转换成赋权完全图模型WCG=〈V,E,W〉,其中V、E和W分别代表WCG中的点集、边集和权重集.GenWCG函数实现的伪代码如下: 图1 MNC算法的基本流程图Fig.1 Flow diagram of MNC algorithm 函数GenWCG(SN) 过程: Step 1. 点集V=SN Step 2. 边集E=V×V 输出:赋权完全图WCG=〈V,E,W〉 采用图论中的经典Prim算法[11]生成最小生成树,即:构建两个点集P和Q,分别代表已在MST和未在MST中的点集合,每次迭代时从Q中选择距离P最近的点加入P,直至Q为空(所有点都已在MST中).生成最小生成树的函数GenMST实现的伪代码如下: 函数GenMST(WCG) 输入:赋权完全图WCG=〈V,E,W〉 过程: Step 1.从v中随机选择一点 Step 2.P={v} Step 3.Q=V-P Step 4.whileQ≠∅ do MST=MST∪{ei,j} endwhile 输出:最小生成树MST={ei,j} 假设SN的最优聚类函数(Optimal Clustering)为OC(SN,CN)其中CN为聚类后的簇个数.定义MST(SN)到OC(SN,M)的投影函数P,其输出为到两个不相交的边集EIntra和EInter,分别为最后聚类结果簇内点间的边集和簇间的边集,即: P(OC(SN,M),MST(SN))=〈EIntra,EInter〉 (1) 其中边集EIntra和EInter满足如下约束: 根据Everitt对聚类的定义“同一类簇的任意两个点间的距离小于不同类簇的任意两个点间的距离”,可得: max(EIntra) (2) 即从最后聚类簇的角度看MST(SN),MST(SN)中连接簇内点最长的边短于连接簇间最短的边. 由于MST(SN)边集的权重空间又可以构成一维的数据空间S1,其中每个数据样本的坐标为MST(SN)中边的权重值,即: S1={di|∀ei∈MST(SN),di=w(ei)} (3) 根据式(1),MST(SN)可以被SN的最优聚类OC(SN,M)划分成两个不相交的子集EIntra和EInter,而且EIntra和EInter间距离足够远.结合式(2)可见MST(SN)投影到OC(SN,M)的过程等价于一维数据S1的2分类过程,即: P(OC(SN,M),MST(SN))⟺OC(S1,2) (4) 根据(4)式,原复杂度较高的“不定类别数的N维空间聚类OC(SN,M)问题”被转换成了复杂度较低的“类别数为2的一维空间聚类OC(S1,2)问题”.实现OC(S1,2)的方法有很多种,但由于OC(S1,2)具备“类别数固定为2”、“距离计算为简单的减法”、“初始重心可选左右端点”等特点,使得经典K-means算法的缺点都可被弥补,因此本文采用经典K-means算法来实现OC(S1,2).在上述结论的基础上,本方案的剪枝阈值生成函数GenPT实现的伪代码如下: 函数GenPT(MST) 输入:最小生成树MST={ei,j} 过程: Step 1.提取MST边集的一维权重空间S1 Step 2.利用经典K-means对S1进行k=2的聚类,即{W1,W2}=kmeans(S1,2),其中max(W1) Step 3.阈值PT=min(W2) 输出:阈值PT 利用上一步得到阈值PT,对MST进行剪枝,即MST中所有权重大于PT的边都被断开.经过剪枝后,原来全连通的MST会变成森林.剪枝函数Prune实现的伪代码如下: 函数Prune(MST,PT) 输入: 最小生成树MST={ei,j} 剪枝阈值PT 过程: Step 1.F=MST Step 2.forei∈MSTdo ifw(ei)≥PTthen F=F-{ei} endif endfor 输出:森林F 经过剪枝得到的森林F中的连通分量可以作为初步的聚类结果,但由于实际数据集中往往包含很多无用的噪声数据,如果不进行过滤,就会降低聚类结果的精度.噪声数据反映在聚类结果中,就是空间密度低且距离正常数据比较远的离群点[12].为了在中检测这些离群点,只需对F的连通分量进行点数判断,本算法视包含的点数少于3的连通分量为离群点.离群点过滤函数Filter实现的伪代码如下: 函数Filter(F) 输入:森林F={ei,j} 过程: Step 1.C=ConnectedComponents(F) Step 2.forci∈Cdo if|ci|<3then C=C-{ci} endif endfor 输出:簇集合C 其中的ConnectedComponeents()函数为连通分量提取函数,实现时可以采用图论算法中经典的Hopcroft算法[13].经过滤后的连通分量即为MNC算法的最终聚类结果. 由于好的聚类算法应该能够处理不同凹凸形状的数据集,所以为了验证本算法的有效性和最后聚类效果的直观可视性,实验首先选择了经典机器学习库scikit-learn[14]中的3组具有不同形状的二维随机数据集DS1、DS2和DS3,三者中包含的簇形状总结如表1. 表1 二维数据集中的数据簇形状 数据集凹凸性簇形状DS1凸凸形DS2混合半圆形+凸形DS3混合环形+凸形 为了进一步证明MNC算法的有效性,本文又选取了三个经典的UCI多维数据集Iris、Wine和Glass.三者的属性数(维度)、样本数、类别数总结如表2. 表2 经典UCI数据集特征 数据集维度样本数类别数Iris41503Wine131783Glass102147 由于传统K-means和MSTCluster都是参数化算法,即输入除了待聚类的数据集外,还需要额外的参数:传统K-means的簇数k和MSTCluster的调节因子λ.而对于不同形状数据集,相应的最优化参数无法提前预知,所以本实验对传统K-means和MSTCluster采取了迭代实验的方式:以两者参数可能取值的最小值为初始值,每次以小步长进行递增,对每个可能的参数都进行聚类实验,并对得到的聚类结果进行评价函数计算,最后当评价函数值达到极小时,我们认为达到最优聚类. 3.2.1 二维随机数据集 对于二维随机数据集,不同聚类算法(经典K-means、基于最小生成树的传统MSTCluster算法和本文MNC算法)的最优聚类效果如图2~图4所示(其中X表示离群点),从中可以得出不同算法对不同形状数据簇的识别能力,总结如表3. 表3 对不同二维形状数据簇的识别能力 聚类算法凸形半圆形环形K-means√××MSTCluster√√√MNC√√√ 可见传统K-means只能识别凸形数据簇,而基于最小生成树的MSTCluster和本文的MNC算法不仅能识别常规凸形数据簇,而且还能够识别半圆、环等非凸的数据簇.分析其原因是与传统K-means直接进行聚类不同,MNC和MSTCluster都采用了先凝聚再分类的间接方式,即先将整个数据集按照最小生成树的方式凝聚成一个大的类,然后分析数据集的整体性质,并在此指导下自顶向下地进行分类.由于充分利用到了数据集的整体性质,所以最后分类的结果相比传统K-means会更加准确. 图2 二维数据集DS1的聚类效果Fig.2 Clustering result of DS1 图3 二维数据集DS2的聚类效果Fig.3 Clustering result of DS2 图4 二维数据集DS3的聚类效果Fig.4 Clustering result of DS3 而对比MNC和MSTCluster之间的聚类结果,可以发现MNC比MSTCluster更优:DS2中的两个半圆形簇和DS3中的两个环形簇,MSTCluster都没有进行区分,而MNC成功进行了区分.上述结果说明MSTCluster迭代实验停止时还并未到达真正的最优,而不同形状数据集的最优化λ参数是无法提前预知的. 3.2.2 经典UCI数据集 对于经典UCI数据集,由于其高维特性,无法直观展示聚类效果,故采用经典聚类评价指标中的RAND系数来进行评估.RAND系数反映的是对于有参考标签(比如Iris数据集中花的类别)的数据集,实际聚类结果与参考结果间的相似度[15],其取值范围在[0,1]之间,值越大表示聚类结果的准确度越高.本文选取Iris、Wine、Glass三种UCI数据集进行聚类实验,不同聚类算法的RAND系数统计如表4. 表4 UCI数据集聚类后的RAND系数 聚类算法IrisWineGlassK-means0.430.160.31MSTCluster0.520.270.41MNC0.660.330.56 由上述结果可见,针对三种实际的数据集,三种不同聚类算法中,MNC算法的RAND系数都是最大的,传统K-means算法的RAND系数最小.此结果说明不仅针对前述随机数据集,对于Iris等实际数据集,本文的MNC算法相对传统K-means等算法仍然能提供更高的聚类准确率. 迭代实验中传统K-means的输入参数(簇数k初始取值为2、迭代步长为1)和MSTCluster的输入参数(调节因子初始取值为1、迭代步长为0.2)的最终取值总结如表5. 表5 输入参数的迭代统计 聚类算法输入参数最终取值DS1DS1DS2IrisWineGlassK-means簇数k 665337MSTCluster调节因子λ1.61.62.02.21.82.0 从上述结果可见针对不同形状数据集,传统K-means和MSTCluster的输入参数在迭代停止时各不相同.由于不同形状数据集的最优化参数无法提前预知,所以本文MNC算法的非参数化特点具有很大优势. 3.2.3 运行时间统计 不同数据集下各聚类算法的运行时间统计如表6,时间单位为秒.(由于K-means和MSTCluster采用了多次迭代实验的方式,因此这两者的运行时间采用的是多次迭代的均值) 由表6的结果可见,对所有数据集,K-means时间最长,MSTCluster次之,MNC最短.具体6个数据集下MNC相对传统K-means的优化比例分别为37%、47%、50%、50%、45%和46%,相对MSTCluster的优化比例分别为17%、26%、30%、25%、29%和28%.分析其原因是K-means算法每次迭代时都要重算所有数据对象与各簇新中心间的欧式距离,而每次欧式距离的计算除了加、减等简单运算,还有复杂的平方和开方运算,在MSTCluster和MNC中,数据对象间欧式距离的计算只会在算法的第一阶段进行一次,后续两个阶段中都只有简单的加、减和比较操作,所以相比传统K-means,MSTCluster和MNC的计算复杂度更低.而MSTCluster和MNC之间相比,虽然两者前期都基于最小生成树,但不同的是MSTCluster中剪枝阈值的产生需要依赖经验参数(调节因子),而MNC的剪枝阈值则是根据最小生成树自动产生,避免了对参数空间的最优搜索过程,所以MNC的计算复杂度相比MSTCluster更低. 表6 运行时间统计 数据集K-means/sMSTCluster/sMNC/sDS10.0140.0110.009DS20.0470.0300.025DS30.0750.0500.037Iris0.1200.0800.060wine0.1380.1060.075glass0.1590.1190.086 综上所述,本文的MNC算法不仅对不同形状的二维随机数据集和经典高维数据集能够有效聚类,而且无参数化的特点使得算法的计算复杂度相比传统算法能够进一步优化. 为了解决K-means算法对初始聚类数k和初始簇中心经验参数的依赖问题,本文提出了一种只依赖数据集本身而无需经验参数的新型无参数化聚类MNC算法.该算法首先依据最小生成树理论将整个数据集凝聚成一个大类,然后利用传统聚类算法对最小生成树边集的一维权重空间二次聚类得到簇内边集和簇间边集,最后以此为依据对最小生成树进行剪枝而得到连通分量,该连通分量即为聚类的簇.为了验证该算法的有效性和实用性,本研究还通过实验分析对比了不同聚类算法的准确度和复杂度.实验结果表明,MNC算法不仅能够准确识别不同形状的数据簇,还可以消除传统算法对参数空间的迭代搜索过程,从而降低计算复杂度,提高聚类效率.2.1 符号说明
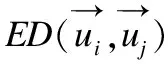
2.2 算法流程
2.3 生成赋权完全图
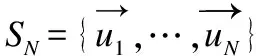
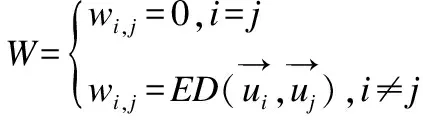
2.4 生成最小生成树
2.5 生成剪枝阈值

2.6 剪枝分裂
2.7 离群点过滤
3 实验与分析
3.1 实验描述
Table 1 Data cluster shape of 2D datasets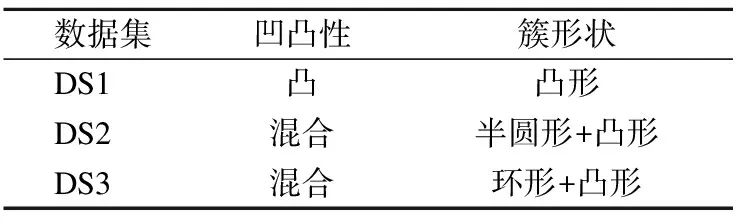
Table 2 Characteristic of UCI datasets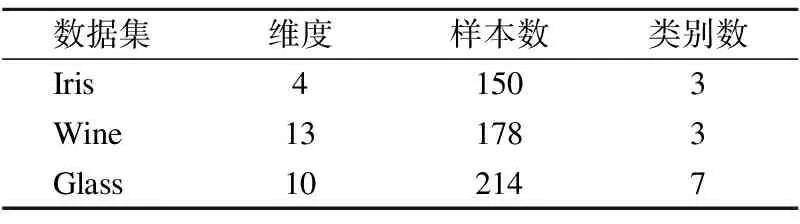
3.2 实验结果与分析
Table 3 Cluster identification ability of different 2D shapes

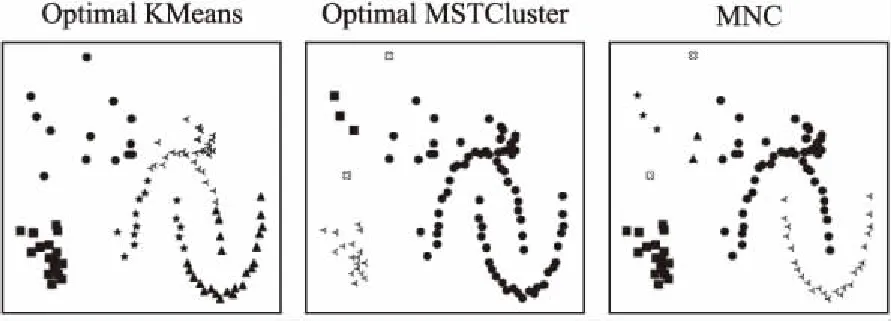

Table 4 RAND coefficients for UCI datasets clustering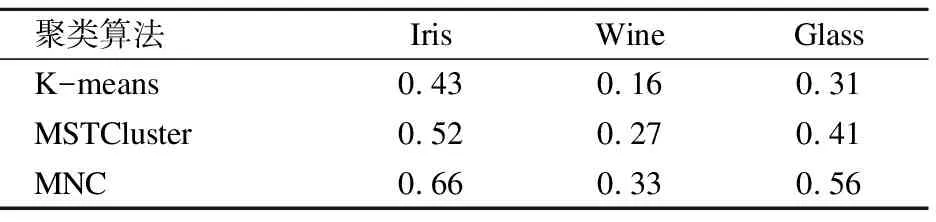
Table 5 Statistics of iterative input parameters
Table 6 Statistics of runtime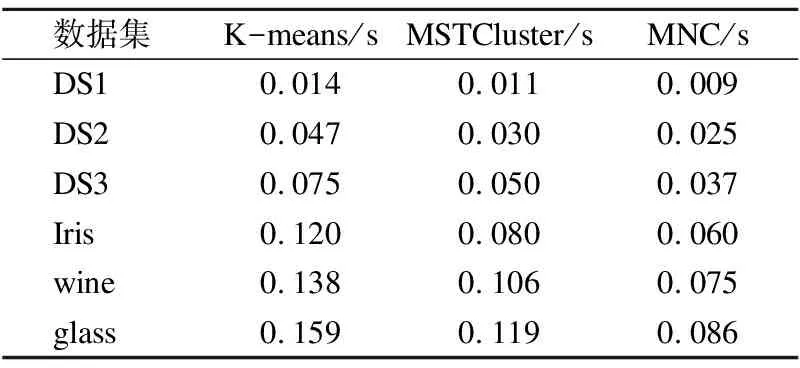
4 总 结
