浅议初中生数学审题能力的培养

卢恒充

每次学生考完试后，在纠错中找错因时总会有不少学生写到：审错题或看错题的问题，那么为了让我们的学生避免出现类似的情况，我们作为数学老师应该在平时教学中培养他们先认真审题再做题的良好学习习惯，逐步培养学生缜密地思考问题及严谨做事的处事态度。本文结合本次课题研究活动中发现的问题及本人多年的教学实践就“如何培养学生审好题”这一主题谈一下自己的看法和做法。

一、学生审不好题的现状分析

根据与学生的沟通调查了解到目前学生经常审错题的原因有一下几点：

1.为了赶时间

初中数学考试时间通常只有2小时，特别是中考要考初中六册书的内容，所以一分试卷的容量大，而且还要思考、计算、书写答题过程都需要时间，所以很多学生在考试中为了赶时间是而忽视审题，往往审题只是一扫而过，结果审错题就不足为怪了。

2.按习惯或凭感觉去做题，思维定势导致错

我们的学生做题多了，特别是考试中在同一位置的题目学生往往就会范这种错。

3.知识链断节

数学知识就像单车链一样，只要其中一节断了，就带动不起车轮来。

4.学生的阅读理解能力低或生活阅历不足

二、审题的界定及其重要性

审题就是阅读、理解题目中涉及的数学知识，明确题目中所提供的条件和要求的结论。审题是解题的第一步，是正确解题的前提。如果考试中审题出了问题，那么再做下去也是“杨白劳打工”——白做。比如题目是：作△ABC关于X轴对称的△A1B1C1，你没看清题目要求，习惯性地按课堂上练习的作成了关于Y轴对称的图形。即使你做的图形是对的，但位置不对也是一分都不得。审题的重要性可以用一句话概括为“差之毫厘，距之千里”！

三、初中生审题能力培养的策略

1.端正审好题的思想态度

平时教学中不断渗透正所谓“磨刀不误砍材工”的思想，让学生意识到审题的重要性，重视审题。

2.放慢审题速度，跳出思维定势

借用提醒开车司机的一句话“宁停三分，不争一秒”来说明这点吧：审题时要求学生不急不躁、不赶，否则会欲速则不达。通过纠错让学生认识到：越是简单的题目迷惑性越大，所以越要审好题再做题，更不能凭感觉去做题。

3.教师在课堂上给与适当的解惑

我们老师在课堂教学中要了解学生在审题上的疑惑点，如果知识链断了，那就得帮他们修复回来，特别是在考察的知识点较综合的题目。

4.审题方法的指导

审题的步骤一般分三个步骤：初审、再审、精审。

（1）初审是要解决已知什么，求什么的问题：第一次读题要在理解题意的基础上搞清已知了什么量，要求什么量，题目所涉及的数学知识;找到关键词，抓住中心意思;题目隐含的条件

（2）再审就要解决已知和未知之间有什么联系的问题：第二次读题要找等（或不等）量关系;由已知量和要求的量你想到了什么知识，它们之间有什么联系等。

（3）精审就是要解决怎么求的问题：第三次读题思考解题方法与途径有哪些，选择哪个最优，表达的顺序等。

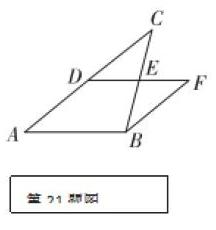
21. （8分）如图，DE是△ABC的中位线，延长DE到F，使EF=DE，连接BF.

（1）求证：BF=DC;

（2）求证：四边形ABFD是平行四边形.

这个题目审题的三个步骤是：

初审应弄懂：已知是“DE是△ABC的中位线”和“线段EF=DE”、“延长DE到F”即说明点D、E、F 在同一直线上;要求的结论是“线段BF=DC”和“四边形ABFD是平行四边形”，并要求学生边读题边用笔在图中用相同的标志标出已知的量与未知的量如用两斜线“＼＼”标在线段EF与DE上，用两个“？”号标在线段BF与DC上。题目涉及到了：三角形的中位线、平行四边形的判定、线段相等数学知识，还隐含了∠DEC=∠FEB这一条件。

再审就是第二次读题时要搞清楚已知的等量关系是“线段EF=DE”，由“DE是△ABC的中位线”应该想到三角形的中位线的定义与它的性质即由三角形中位线的定义知道点D、E分别是线段AC、BC的中点，也就是知道了线段CD=AD、CE=BE;由三角形的中位线性质可以想到DF∥AB、DE=AB;再由平行線的性质可知：∠CDE=∠F、∠C=∠FBE，第一个问题中要求两线段相等，又由刚刚得出的有角相等与线段相等，从而联想到用三角形全等就将它们联系起来了。第二问求“四边形ABFD是平行四边形”我们就应该想到平行四边形的判定方法有五种这么多，根据前面有“中点”和“平行”这两点应该想到它们间的联系是四边形的对角线及一组对边平行且相等的判定。

精审这步就是第三次读题时就要思考用什么方法去证明了：第一问要证两线段相等4用的方法是三角形的全等，这里用“SAS”、“AAS”来证明都可以，但用“AAS”证的话除了用到三角形的中位线性质外还要用到平行线的性质，而如果用“SAS”证的话可以由三角形中位线的定义及对顶角相等这个隐含的条件还有已知中的“EF=DE”条件就可以证明，相对来说会更直接些！证明顺序为：由“DE是△ABC的中位线”得出点E是BC的中点就可以得出CE=BE，再由“∠DEC=∠FEB和EF=DE”就可以证明△DEC≌△FEB，再由全等三角形的性质可以得出BF=DC。第二问考虑如果用平行四边形的定义“有一组对边平行且相对的四边形是平行四边形”来证明的话可以想到找AD与BF或AB和DF这两组线段，但有发现已知中未涉及到线段AB所以不考虑AB和DF这组，就应该考虑证AD和BF这组线段平行而且相等了，而由“DE是△ABC的中位线”知道点D是AC的中点从而AD=CD，又转到证CD和BF平行而且相等即可，而前面已经知道“线段EF=DE”、“CE=BE”只要连接D、B和C、F，构造出以DF、CB为对角线的四边形就可以得出它是平行四边形，从而得出CD和BF平行而且相等，就得出AD和BF平行而且相等即可证明四边形ABFD是平行四边形

总之，只有让学生明白了审题的重要性;端正审题的态度;放慢审题速度，跳出思维定势;教师在课堂上给与适当的解惑（给学生补上断了的知识链）;并给与审题方法的指导——审题的步骤一般分三个步骤：初审、再审、精审，还要学生在平时的学习中不断地实践，才可以不断的提高个人的审题能力。