数学问题解答

2019年12月号问题解答

(解答由问题提供人给出)

2516设x，y，z均为正数，求证：

(湖北省公安县第一中学 杨先义 434300)

证明记A=xyz(x3+y3+z3)，

B=xyz(x2y+xy2+y2z+yz2+z2x+zx2)，

C=x4y2+x2y4+y4z2+y2z4+z4x2+z2x4．

原不等式

⟺64(x+y+z)3xyz≤27((x+y)(y+z)(z+x))2

⟺64A+30B+276x2y2z2≤54A+27C+54(x3y3+y3z3+z3x3)+162x2y2z2

⟺10A+30B+114x2y2z2≤27C+54(x3y3+y3z3+z3x3)．

(1)

易证，

引理1：设a，b>0，则a3+b3≥ab(a+b)．

引理2：设a，b>0，则a4+b4≥ab(a2+b2)．

由引理1，有

2(x3y3+y3z3+z3x3)

=x3(y3+z3)+y3(z3+x3)+z3(x3+y3)

≥x3yz(y+z)+y3zx(z+x)+z3xy(x+y)=B

⟹54(x3y3+y3z3+z3x3)≥27B．

(2)

由引理2，有

C=x2(y4+z4)+y2(z4+x4)+z2(x4+y4)

≥x2yz(y2+z2)+y2zx(z2+x2)+z2xy(x2+y2)

=B

⟹3C≥3B.

(3)

又C=x4(y2+z2)+y4(z2+x2)+z4(x2+y2)

≥x4·2yz+y4·2zx+z4·2xy=2A

⟹5C≥10A．

(4)

显然有C≥6x2y2z2⟹19C≥114x2y2z2．

(5)

(2)+(3)+(4)+(5)，即得(1)，因此原不等式获证．

图1

(北京市朝阳区芳草地国际学校富力分校 郭文征 郭璋 100121)

证明如图2，过点B2作B2G∥E2C2，交AC2的延长线于点G.

图2

则有∠GB2C2=∠B2C2E2.

因为⊙O的弦B1C1∥B2C2，且B1C1=B2C2，

易证∠AC1B1=∠AC2B2=90°.

因为C2F2⊥AO2于点F2，

所以∠O2C2F2=∠O2AC2.

所以∠GB2C2=∠O2AC2.

所以Rt△B2C2G∽Rt△AC2O2.

①

②

③

④

由③+④得

当且仅当⊙O的弦B1C1与B2C2合并为⊙O的直径BC时，不等式中的等号成立.

2518设P是△ABC内的任意点,三条边长、外接圆半径与内切圆半径、点P到三边BC，CA，AB的距离分别为a,b,c,R,r,x,y,z则有

(天津水运高级技工学校 黄兆麟 300456)

证明首先证链中第一个不等式，

即链中第一个不等式成立.

再证链中第二、第三、第四个不等式，

⟺a2+b2+c2≥bc+ca+ab

⟺(b-c)2+(c-a)2+(a-b)2≥0，

即链中第二、第三、第四个不等式均成立.

接下来证链中第五、第六个不等式，

即链中第五、第六个不等式成立.

接下来证明链中第七个不等式，注意到有，

即链中第七个不等式成立.

最后证明链中第八个不等式，

由三角形面积公式立得，

那么就有

即链中第八个不等式成立.至此定理全部获证.

2519在△ABC中，AB>AC>BC，D，E，F，G四点分别在射线AB，CB，AC，BC上，且满足AD=CE=AC及AF=BG=AB，证明：△BDE的外心O1和△CFG的外心O2到点A的距离相等.

(河南辉县一中 贺基军 453600)

证明如图，连接O1D，O1B，O2C，O2F及DC，FB.

由题设AD=AC，AB=AF知

DB=CF且DC∥FB，

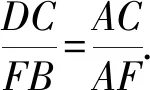
由上式和题设AC=CE，AF=BG知

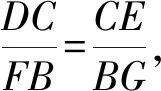
由DC∥FB知∠DCE=∠FBG，

综上得△DCE∽ △FBG，

因此∠DEC=∠FGB，即∠DEB=∠CGF.

因O1，O2分别为△BDE和△CFG的外心，

故△DO1B和△CO2F都是等腰三角形.

根据圆心角与圆周角的关系得

∠DO1B= 2∠DEB，∠CO2F= 2∠CGF，

从而有∠DO1B=∠CO2F.

又因这两个等腰三角形的底边相等，

即DB=CF，故△DO1B≌△CO2F，

从而有O1B=O2F，∠O1BA=∠O2FA.

又因AB=AF，故△O1AB≌△O2AF，

从而有O1A=O2A.

2520设△ABC的三边长、相应旁切圆半径、外接圆半径、内切圆半径和半周长分别为a，b，c，ra，rb，rc，R，r和p, 则有

等号当且仅当△ABC为正三角形时成立.

(安徽省太和县第二小学 任迪慧)

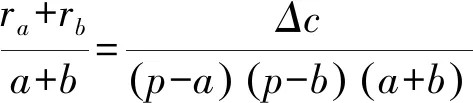
(1)

(2)

(3)

(1)+(2)+(3)整理得

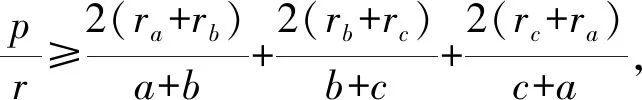
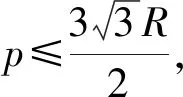
2020年1月号问题

(来稿请注明出处——编者)

2521在△ABC中，设三内角A,B,C所对的三边长分别为a,b,c，三角形面积为Δ，求证：

(1)

(河南质量工程职业学院 李永利 467000)

2522如图，凸四边形ABCD内接于圆O，对角线AC,BD相交于点P，△ABP，△DCP的外接圆相交于P,Q，△ADP，△BCP的外接圆相交于P,G,求证：O,P,G,Q四点共圆.

(安徽省岳西县汤池中学 杨续亮 苏岳祥 246620)

2523已知a、b、c为正实数，试证：

(*)

(浙江湖州市双林中学 李建潮 313012)

2524设点O,Ia,Ib,Ic分别为△ABC的外心和旁心，R为其外接圆的半径，证明： 6R≥OIa+OIb+OIc.

(安徽省枞阳县宏实中学 江保兵 246700)

2525设x,y为实数，满足 (x-4)2+(y-4)2=4 ，求xy的最大值和最小值.

(武汉职业技术学院商学院 邹 峰 430074)