面积法推导数列{n}、{n2}、{n3}的前n项和公式①

王 彬 王 占 侯晓婷 李春兰

(内蒙古师范大学数学科学学院 010022)

数列与函数、不等式等有着密切的联系，又是今后学习高等数学的基础内容之一.其中等差数列作为一种特殊的数列，是高中生探究特殊数列的开始，它对后续数列的学习无论是在内容上还是在方法上都具有积极的意义.

古文献中关于等差数列的前n项和公式的推导方法，如倒序相加法、数形结合法等，也是我国高中数学教科书中惯用的方法.在我国现行6套高中数学教科书中关于等差数列的前n项和公式的推导，人教A版(2007年)、沪教版(2007年)是利用高斯的算法推导得出公式；北师大版(2010年)是先通过如何计算圆木料堆中木料的总数，引出如何计算等差数列的前n项和这个问题，再介绍高斯的算法最后推导得出公式.(6)刘绍学,钱珮玲,章建跃.普通高中课程标准实验教科书数学5必修(A版)[M].北京:人民教育出版社,2007:48-49.人教B版(2007年)和苏教版(2005年)先呈现某仓库堆放的钢管总数图(如图1)，再通过求钢管总数推导出等差数列的前n项和公式；湘教版(2007年)是呈现某学校运动会开幕式的队列站法图(如图2)，再通过求队列总人数推导出等差数列的前n项和公式.

图1

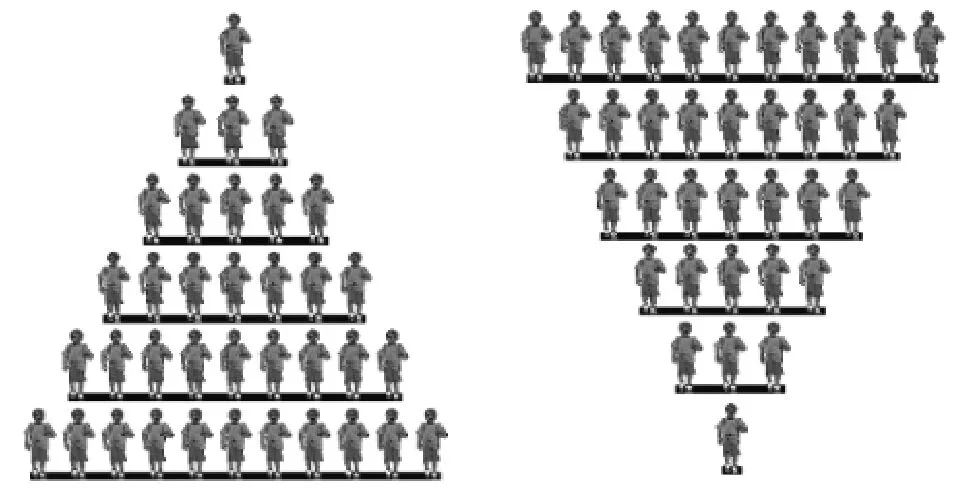
图2

这6套教科书中关于等差数列的前n项和公式的推导，无论是通过高斯的算法进行公式推导，还是先观察钢管图或者队列图再进行公式推导，它们本质上都是应用了加法结合律，首末两端距离相等的每两个数的和都等于首末两数的和，属于代数方法中的倒序相加法.但是只通过高斯算法来推导公式，学生仅仅是利用倒序相加法对等差数列的前n项和公式进行死记硬背；若加入图形来理解倒序相加法再推导公式，可以建立学生对于形与数的联系，借助几何直观更好的理解公式的推导过程.

本文主要介绍民国时期著名数学家、数学教育家、出版家刘薰宇(7)刘薰宇(1896—1967)贵州贵阳人，又名心如.毕业于北京高等师范数理系，受过法国教育的熏陶.他毕生论著颇丰，以小品文、科普著作、数学教科书为著称.先生在其科普著作《数学趣味》(8)《数学趣味》是刘薰宇于1934年出版的数学科普著作.本书是由11篇发表在《中学生》《一般》《春晖》三个杂志中的论文集结成的单行本.中如何推导数列{n}、{n2}、{n3}的前n项和公式，即从“面积法”视角推导每个数列的前n项和公式.

1 数列{n}的前n项和公式推导

对于等差数列{n}的前n项和公式的推导，刘薰宇在《数学趣味》中由堆罗汉(9)“堆罗汉”是学校中常见到的一种游戏，它是从最下面一排起数上去，每排都少一个人，直到顶上只有一个人为止.在数学中像这类依序相差同样的数的一列数，在数学上我们称它为等差级数，最简单的等差级数就是我们所学的等差数列.游戏引出问题，将堆罗汉游戏中的每个人抽象为边长为1的正方形，通过求面积得出数列{n}的前n项和公式.此方法是利用数形结合，从特殊到一般，将求数与数之和的问题转化为求几何图形的面积问题，方法简单易懂，妙趣横生.

刘薰宇将一个从1起到某一个数为止的若干个连续整数的和用下面的(1)式来表示.

1+2+3+4+5+6+7+…+n

(1)

借助堆罗汉游戏，将7人为底的堆罗汉抽象为图3，再将图3变形为图4.他利用图5中的A部分表示了式子(1)中的前7项之和，B部分恰好是A部分的倒置，A、B两部分组合成了图中的矩形，图中每一方格的边长记为单位1，即每一小方格的面积也为1.所以，A、B两部分的面积分别记为

图3

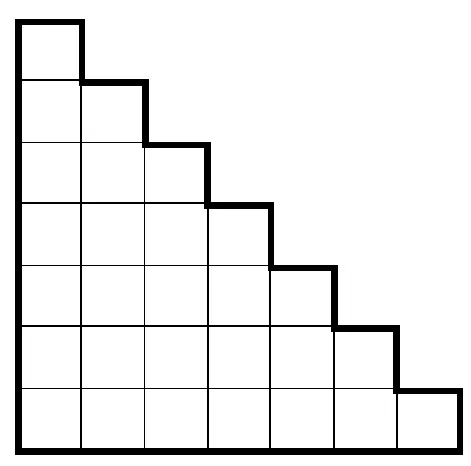
图4

图5

图6

A=1+2+3+4+5+6+7,

B=7+6+5+4+3+2+1,

此时，求式子(1)的前7项之和，转化为求图5中A部分的面积，因A、B部分的面积相等，且各部分面积等于图5这个矩形面积的一半.该矩形的长是7，宽是7+1，因此面积便是

7×(7+1)=7×8=56,

将上式推广到一般情形变为

上式也就是等差数列{n}的前n项和(n∈N*).

我们再从特殊到一般(如图6，其中a1和d都代表了小方格的面积，且d为单位正方形的面积)，可得到等差数列的前n项和公式

刘薰宇借助“堆罗汉”游戏对等差数列{n}的前n项和公式进行了推导，利用了数形结合的思想方法，直观形象地将等差数列的前n项和问题转化为求矩形的面积问题，化数为形，体现了图形之美，数形之幻.若在教学中将“堆罗汉”游戏与图形加入到等差数列{n}的前n项和公式的推导和公式的理解中，会为教学增添些许趣味与生动性，还可渗透数形结合的思想方法.让学生亲身经历探索数列求和公式的旅程，既培养了学生的逻辑思维、提高直观形象的能力，还能感受数学公式之美.

2 数列{n2}、{n3}的前n项和公式推导

教科书中数列{n2}、{n3}的前n项和公式的推导一般是以课后拓展题的形式给出，老师的讲解多数是利用代数方法，公式推导过程十分繁琐.而刘薰宇不仅运用“堆罗汉”游戏直观形象地推导出等差数列{n}的前n项和公式，还对数列、{n2}{n3}的前n项和公式利用面积方法进行了推导.

2.1 数列{n2}的前n项和公式推导

从1起到某数为止的各整数的平方和用式子表示出来就是下面的(2)式.

12+22+32+42+52+62+72+…+n2

(2)

图7

如图7，每个小方格均为单位正方形，(2)式的前7项可用图5表示出来，而22恰好等于从1起的2个连续奇数之和；32等于从1起的3个连续奇数之和；以此类推，72就是从1起的7个连续奇数的和.因此求12+22+32+42+52+62+72，只需要将上面7个式子的右边相加即可.虽然这个方法能够得到正确答案，但不够简便，而且不易从中找出一般性的式子.因此刘薰宇利用堆罗汉的方法，将上面式子的右边用堆罗汉的方式堆起来，为了叙述简便，n只取到4，抽象出图8.

图8

图9

图10

图11

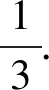
则可以得到

上式就是求数列{n2}的前n项和.

2.2 数列{n3}的前n项和公式推导

从1起到某数为止的各整数的立方和用下面(3)式表示出来.

13+23+33+43+53+63+73+…+n3

(3)

因为数是立方的关系，先想到的可能是用立体图形来表示，但在平面上不利于表示.若能联想到乘法的意义，用平面图形来表示一个立方，也是有可能的.为了叙述简便，n仍只取到4.例如23的意义是3个2相乘，式子表示为2×2×2，同时这个式子也可以记为(2×2)×2，可以理解它表示的是2个22的意思.

所以23用图形可表示为图12中的A，再将图12A变换一下可得出图12B.同理，33=(3×3)×3可用图13A或B表示，43=(4×4)×4可用图14A或B表示.

图12

图13

图14

仔细观察图12、图13、图14中的B，可得出如下关系：图12B的缺口恰好是13，所以13能填补23的缺口.图13B的缺口，每个边都是3，这和图12B的外边缘相等，可知13和23可将其缺口填满.图14B的缺口每边都是6，又恰好等于图13B的外边，因此13和23和33拼在一起能将图14B的缺口填满.按照此填法，便得到图15，它恰巧是13+23+33+43的总和.

图15

图15是边长为1+2+3+4的正方形，它的面积是(1+2+3+4)2，因而得到：13+23+33+43=(1+2+3+4)2，该等式右边括号中1+2+3+4按照数列{n}的前n项和公式得

因此

13+23+33+43=(1+2+3+4)2

将上式推广到一般的情形去，得到

13+23+33+43+…n3=(1+2+3+4+…n)2

上式也就是数列{n3}的前n项和.

同(1)式的推导方法类似，(2)和(3)式也仅仅是用1，2，3，4为代表进行观察推导，便得到一般性结论，结果不一定完全可靠，因此刘薰宇也用了数学归纳法对其进行论证，此不赘述.

对于数列{n2}、{n3}的前n项和公式的推导，刘薰宇首先将代数问题转化为几何问题，即代数求和转为求矩形面积.图形以不同的方式罗列起来，也像“堆罗汉”一样.随后变换几何图形的形状，拼凑成一个大矩形，求出大矩形的面积，数列的前n项和问题也就迎刃而解.

3 结语

追溯刘薰宇推导数列{n}、{n2}、{n3}的前n项和公式的思想方法之源，他应该是受到我国南宋数学家杨辉的方法启发，将代数问题转化为几何问题.我国著名数学家华罗庚说过：“数缺形时少直觉，形少数时难入微.数形结合百般好，隔裂分家万事非.”刘薰宇将代数问题几何化，利用面积法推导数列{n}、{n2}、{n3}的前n项和公式，直观、形象、易懂，只可惜他的这种方法在我们当今的数学课堂教学中却几乎无人问津.

我国《普通高中数学课程标准(2017年版)》中对于“等差数列的前n项和”提出的教学目标为：“探索并掌握等差数列的前n项和公式，理解等差数列的通项公式与前n项和公式的关系.”(10)中华人民共和国教育部.普通高中数学课程标准:2017年版[S].北京:人民教育出版社,2017:38.在这部分内容的课堂教学中，完全可以将杨辉、刘薰宇的思想方法融入到教学中，这不但有助于学生真正理解和掌握数列{n}、{n2}、{n3}的前n项和公式，而且可以展示我国传统文化的魅力，实现德育之效.正如汪晓勤所言：“在数学教学中，数学史可以揭示知识之谐，呈现方法之美，营造探究之乐，达成能力之助，展示文化之魅，实现德育之效.”(11)汪晓勤.基于数学史的数学文化内涵课例分析[J].上海课程教学研究,2019:37.另外，在公式的探究过程中学生也可以感受到数学的趣味，激发学生学习数学的热情，将数学“冰冷的美丽转化为火热的思考”.