三角形费马点的再推广

储炳南

(安徽省合肥市第四中学 230601)

1 问题的提出

1640年，费尔马提出如下问题：“在平面上给出A、B、C三点，求一点P使距离和PA+PB+PC达到最小.”这就是数学史上著名的“费尔马问题”.特别地，点A、B、C三点不共线时，使PA+PB+PC最小的点P称为△ABC的费尔马点.

文[1]把费马点问题推广到“两定点、一条定直线”的情形，下面笔者再对“费马点”问题做出如下推广：

推广一在平面内，已知三条定直线l1、l2、l3，在平面内求一点P，使点P到直线l1、l2、l3的距离之和最小.(不考虑“三线共点和三条直线中有平行直线”的平凡情况)

推广二在平面内，已知两条定直线l1、l2和一个定点A，在平面内求一点P，使点P到直线l1、l2和点A的距离之和S最小.(不考虑“点A在直线l1或l2上和l2∥l2”的平凡情况)

2 问题的解决

2.1 推广一的解决

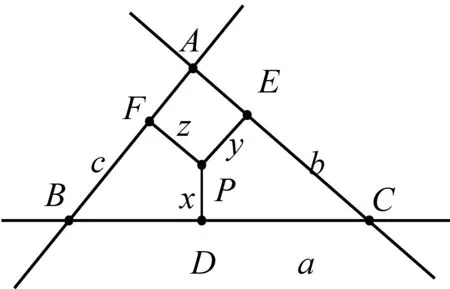
图1

设直线l1、l2、l3两两相交于不同的三点A、B、C，且BC=a，AC=b，AB=c，P点到三条直线l1、l2、l3的距离分别为x、y、z，三角形△ABC的面积为S.为了证明的方便，不妨设a≥b≥c,

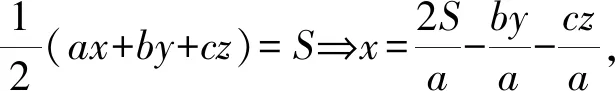
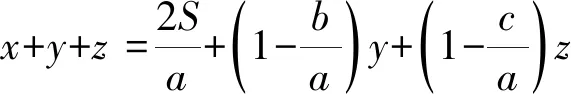
“=”当且仅当y=z=0时成立，即此时点P与点A重合.所以当平面上三条直线l1、l2、l3两两相交于三个不同的点A、B、C时，点P到l1、l2、l3的距离之和的最小值恰为△ABC的最长边上的高，并且最小值在点P与最长边所对的顶点重合时取得.

2.2 推广二的解决

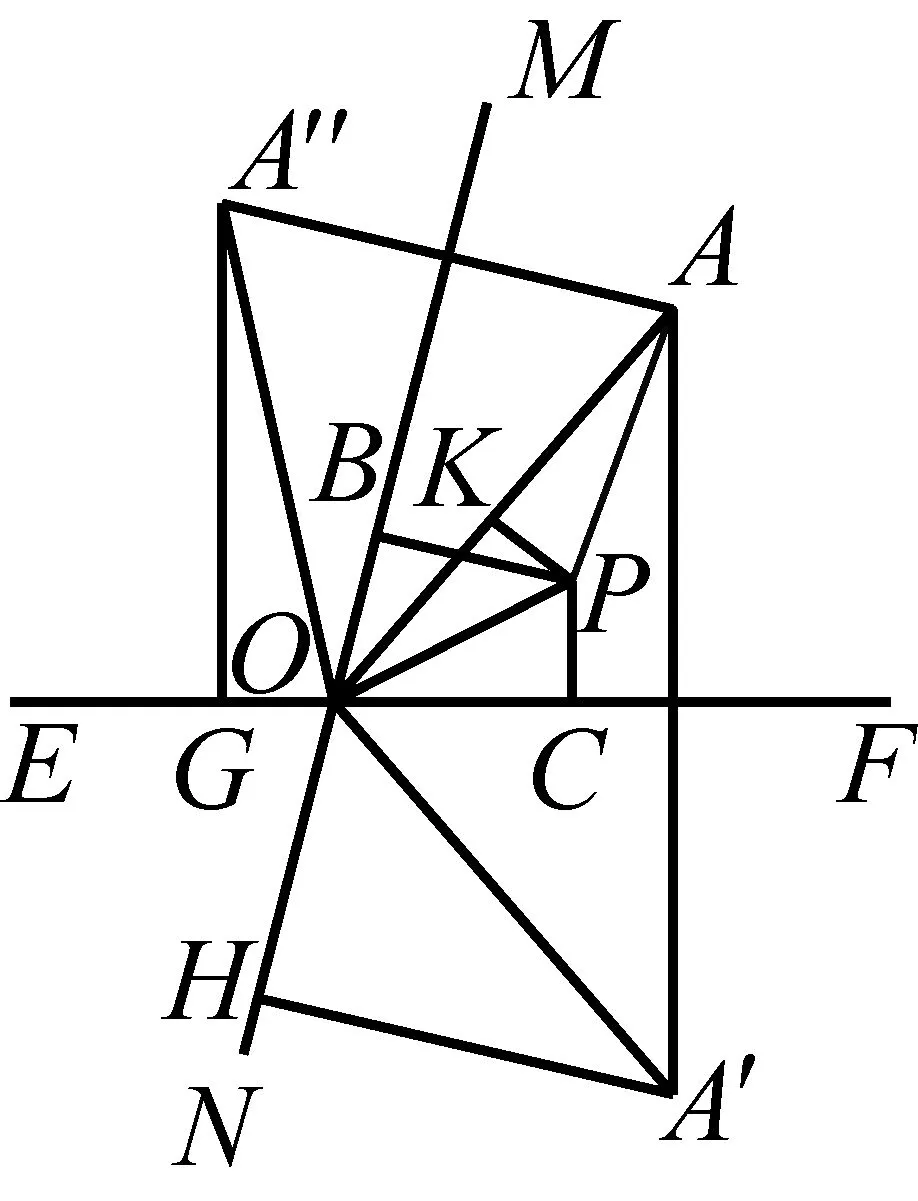
设两条定直线EF与MN相交于点O，定点为A，下面笔者根据EF和MN，以及定点A的相对位置进行分类求解S取得最小值时的最优点.

情形一点A在两直线EF和MN所成的钝角区域内(只需考虑点A在∠MOE内部的情形，点A在∠FON内部的情形同理可证.)过点O分别作直线EF、MN垂直的射线OG、OH，将∠MOE内部分成三个区域，即∠HOE内部，∠HOG内部，∠GOM内部，下面分三种情况：

设点P是平面内任意一点，过点P作PB⊥MN，PC⊥EF，垂足分别为B，C，则S=PA+PB+PC.

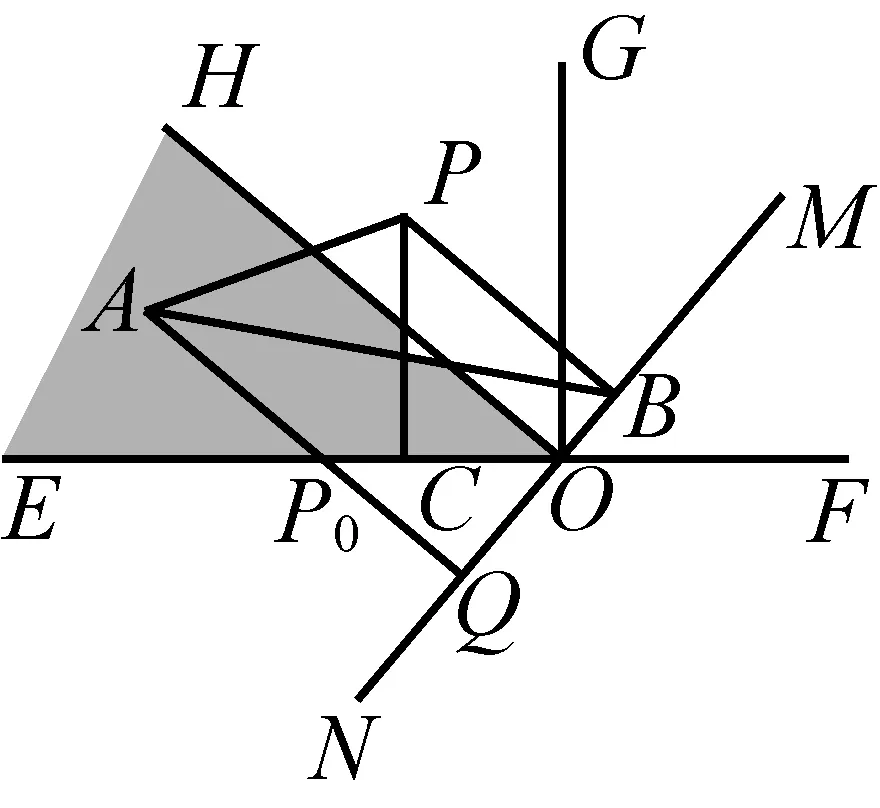
图2

(1)当点A在∠HOE内部(如图2中阴影部分，包括边界)时，过A点作MN的垂线AQ，垂足为Q，此时AQ与EF必相交，记交点为P0，则当P点与P0重合时，S取得最小值为AQ，证明如下：

S=PA+PB+PC≥PA+PB≥AB≥AQ，

“=”当且仅当P与P0重合时成立.

(2)当点A在∠GOM内部(如图3中阴影部分，包括边界)时，过A点作EF的垂线AQ，垂足为Q，此时AQ与MN必相交，记交点为P0，同理可证明当P点与P0重合时，S取得最小值为AQ.

图3

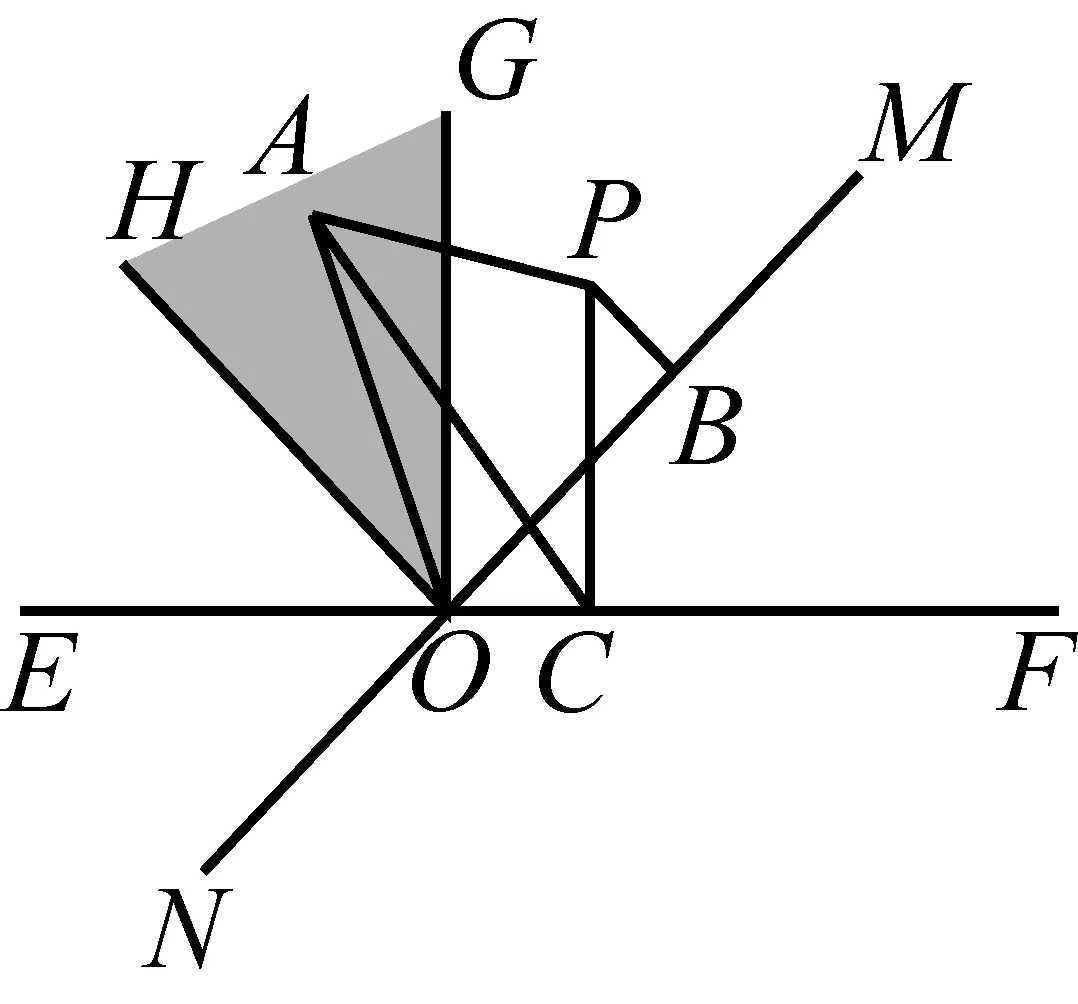
图4

(3)当点A在∠HOG内部(如图4中阴影部分，包括边界)时，下面证明此时O点即为最优点，S的最小值为AO.

①当点P在∠GOM内部(包括边界)时，如图4所示，由于∠AOC≥∠GOC=90°，

所以AC≥AO.

而S=PA+PB+PC≥PA+PC≥AC≥AO，

即S≥AO.

②当点P在∠HOE内部(包括边界)时，如图5所示，类似①，可证：S≥AO.

图5

图6

③当点P在∠HOG内(如图6所示)时，

因为∠POB+∠POC>90°，

所以90°>∠POB>90°-∠POC>0°，

所以sin∠POB>sin (90°-∠POC) =cos∠POC，

所以S=PA+PB+PC

=PA+PO(sin∠POB+sin∠POC)

>PA+PO(cos∠POC+sin∠POC).

因为∠POC为锐角，

所以cos∠POC+sin∠POB>1，

所以S>PA+PO(cos∠POQ+sin∠POQ)

≥PA+PO≥AO，

即S>AO.故无解.

④当点P在∠MOF(或∠EON)内部(包括边界)(如图7所示)时，

S=PA+PB+PC≥PA+PC≥AC≥AO.

综上可知：当点P与点O重合时，S取得最小值.

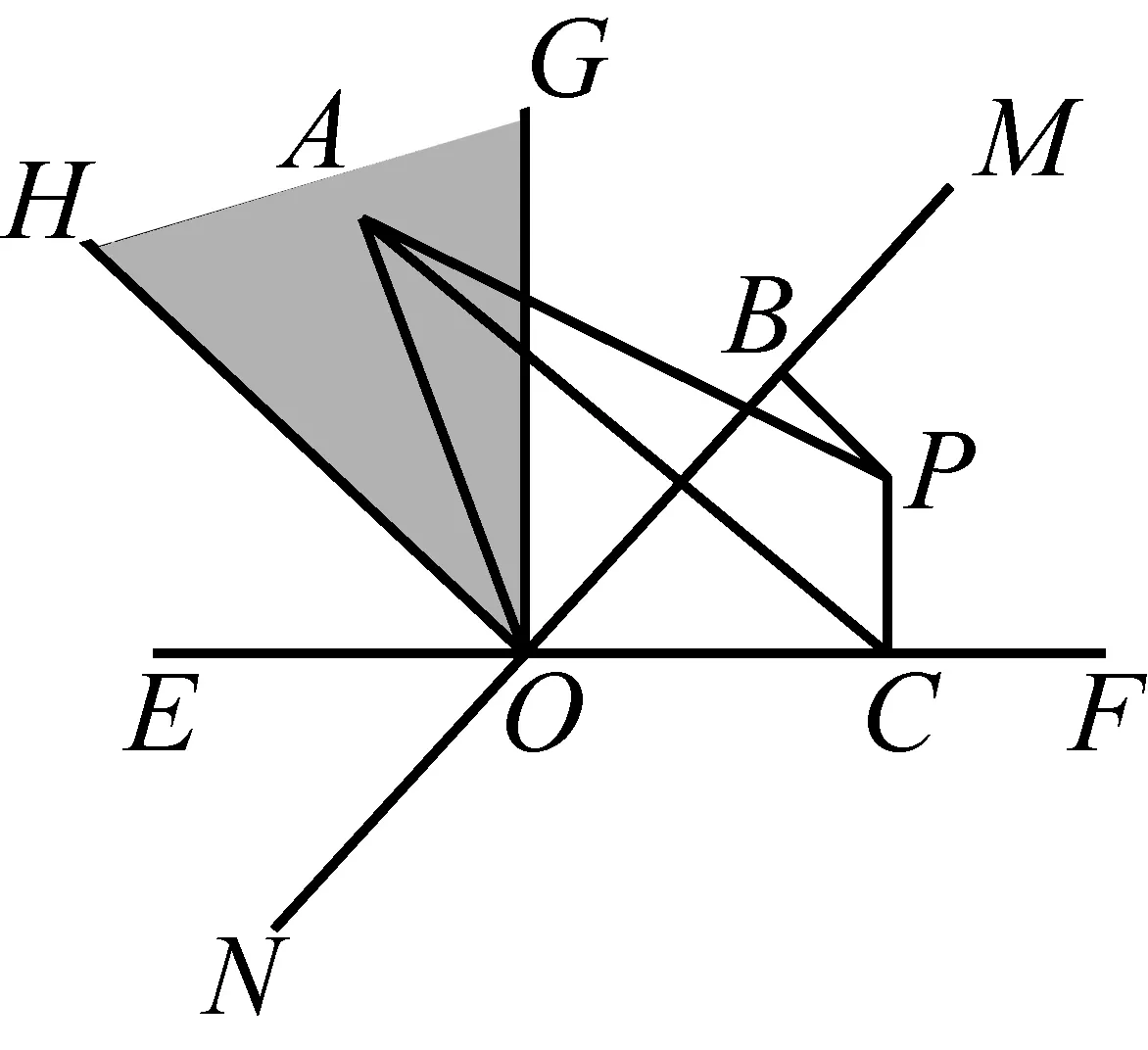
图7

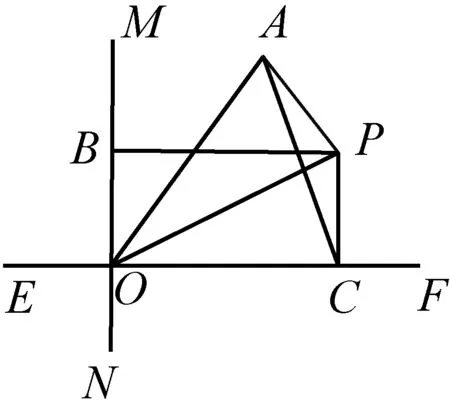
图8

情形二若直线EF与MN的夹角为直角时(如图8所示)

设P是平面内不同于O的任意一点，过点P作MN、EF的垂线,垂足分别为B、C.

因为S=PA+PB+PC≥PA+PO≥AO，

所以当点P与点O重合时，S取得最小值.

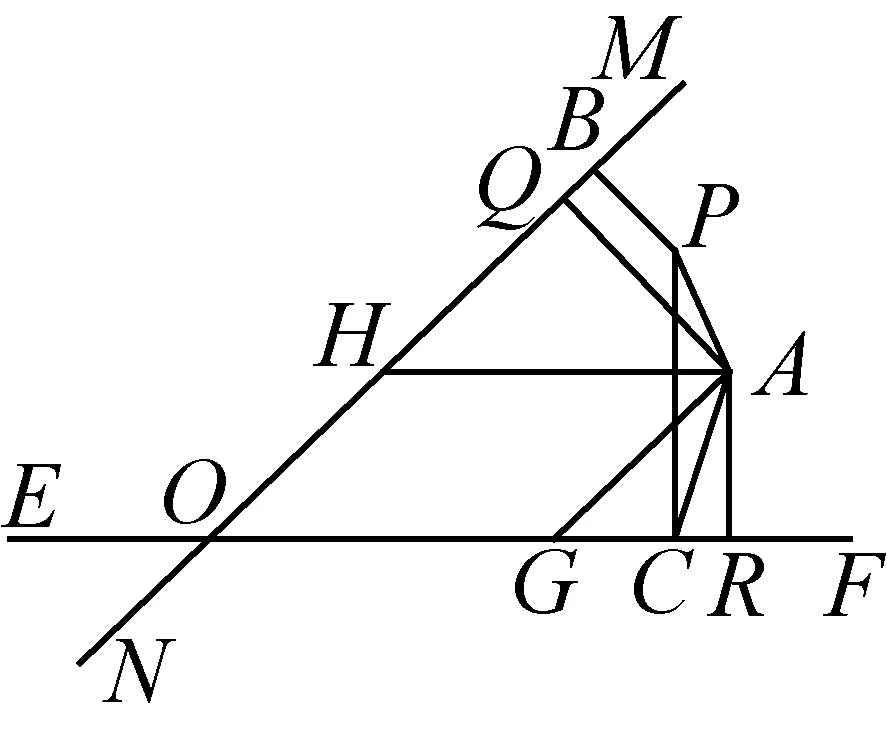
图9

情形三点A在两直线EF和MN所成的锐角区域内时，过点A分别作MN，EF的平行线，交EF、MN于点G、H(如图9所示).

下面首先证明最优点P应在平行四边形OGAH内.

若点P在平行四边形OGAH边AH的上方的区域内，如图9所示，过A、P分别作EF的垂线，垂足分别为R、C，又过A、P分别作MN的垂线，垂足分别为Q、B.

因为PC>AR，且PA+PB≥AQ，

所以PA+PB+PC≥AQ+PC≥AQ+AR，

所以，P点没有A点好，即点P不会在AH的上方的区域内.同理可证，点P不会在AG右边的区域内.

下面再证明点P不会在直线EF的下方.

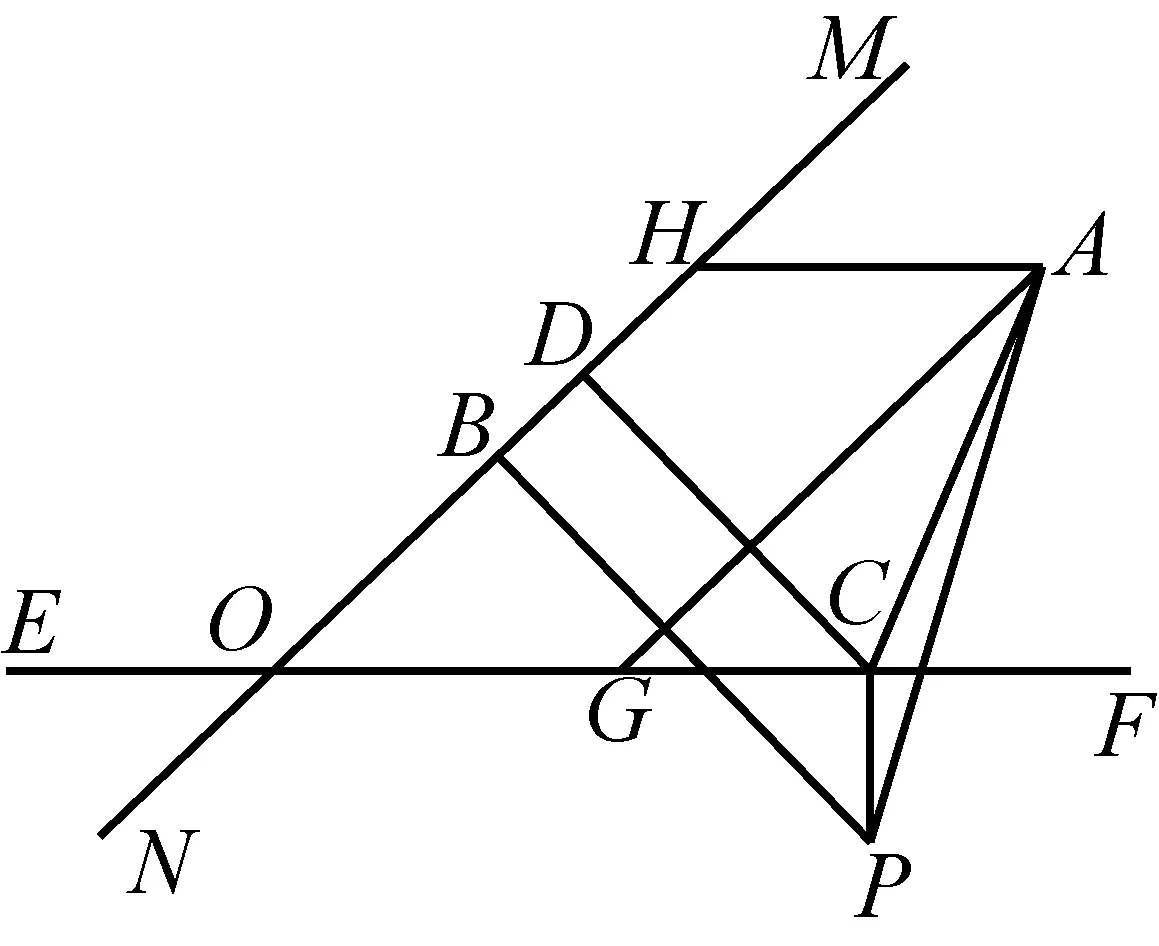
图10

当P点在EF下方时，过点P作PB⊥MN，PC⊥EF，垂足分别为B，C.过点C作CD⊥MN，垂足为D.如图10所示.

因为PA+PC>AC，PB>CD，

所以PA+PB+PC>AC+CD，

所以P不可能在EF的下方.

同理可得P不可能在MN的左边，所以P点的最优点只可能在平行四边形OGAH内部的区域.

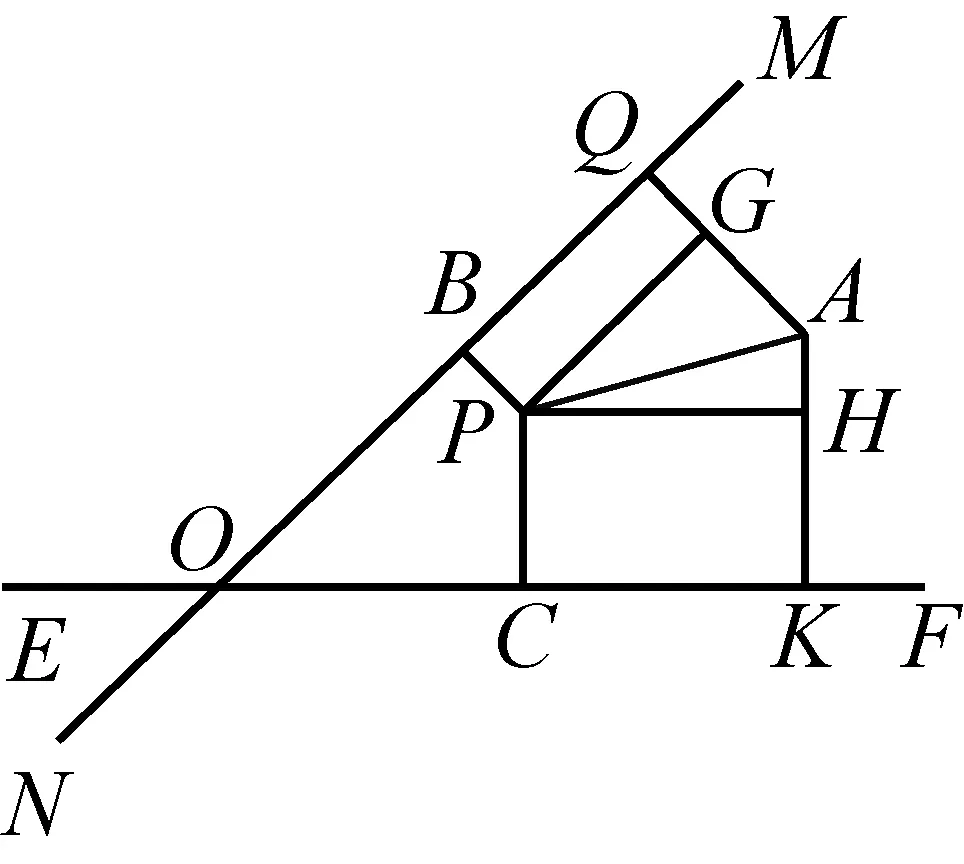
图11

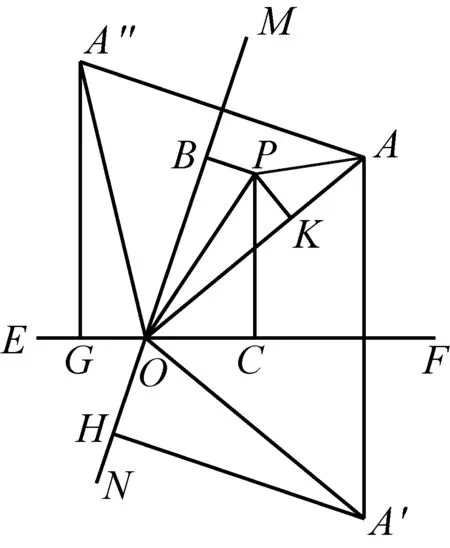
(1)当∠FOM<60°时,P点最优点为点A(如图11所示)，证明如下：

在平面内任意取不同于点A的一点P，过点A分别作EF、MN的垂线，垂足分别为K、Q，又过点P分别作AQ、AK的垂线，垂足分别为G、H，记PA与EF的夹角∠APH=α，PA与MN的夹角∠APG=β，则P点到MN、EF和点A的距离和为：

S=PA+PB+PC=PA+GQ+HK

=PA+AQ+AK-AG-AH

=PA+AQ+AK-PA(sinα+sinβ)

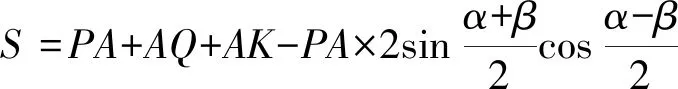
>PA+AQ+AK-PA=AQ+AK,

所以，P点没有A点好，即A点为最优点.

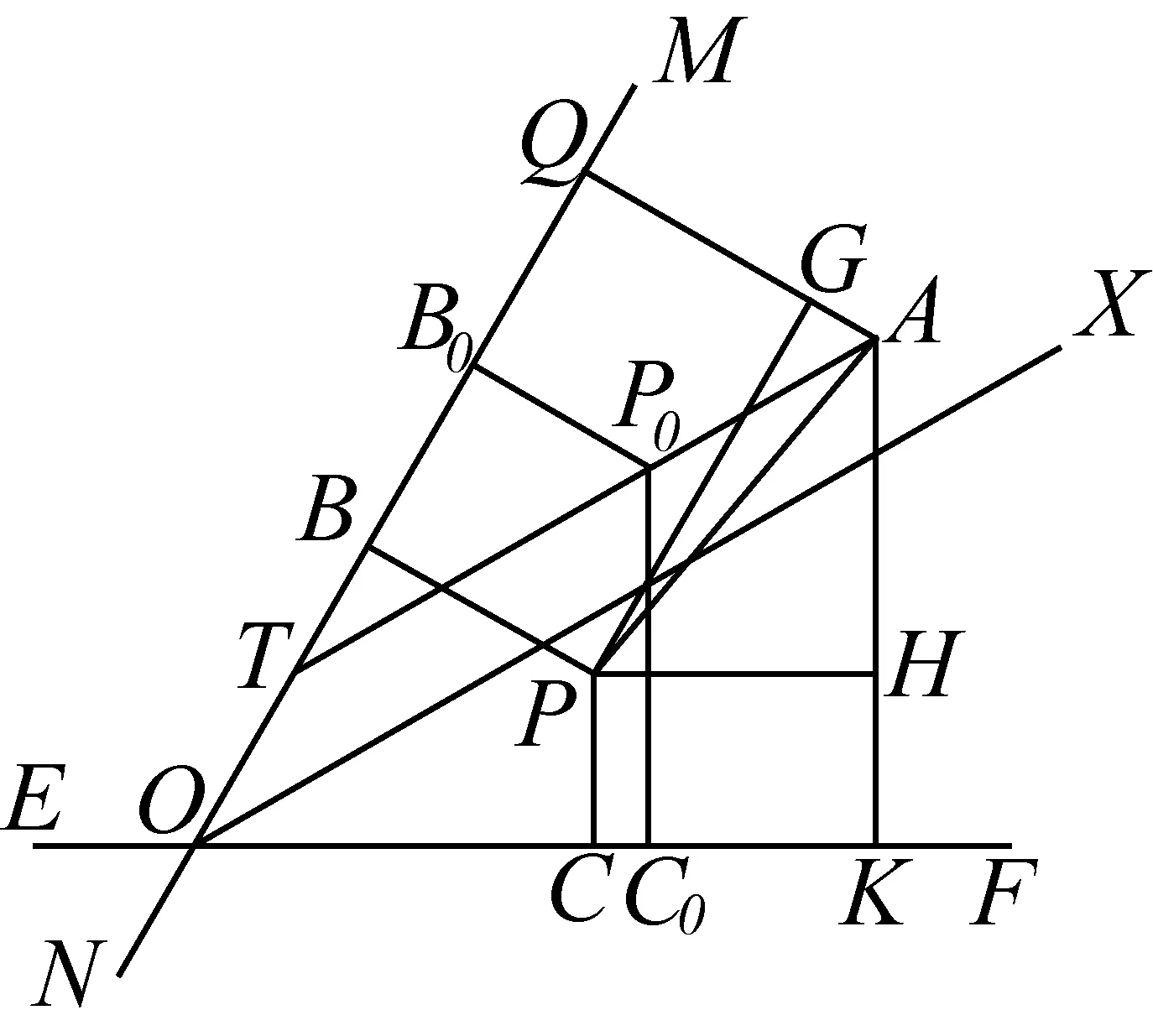
图12

(2)当∠FOM=60°时,记∠FOM的平分线为OX，不妨设点A在OX的上方(包括OX)，过点A作OX的平行线，交MN于点T，可证明AT上任意一点均为最优点(如图12所示).

证明如下:

过点A分别作EF、MN的垂线，垂足分别为K、Q，又过点P分别作AQ、AK的垂线，垂足分别为G、H，记∠APH=α,∠APG=β,

S=PA+PB+PC=PA+GQ+HK

=PA+AQ+AK-AG-AH

=PA+AQ+AK-PA(sinα+sinβ)

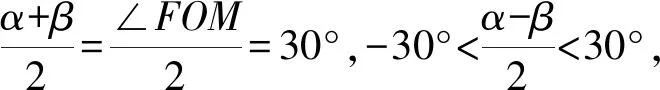
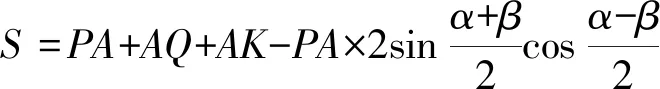
≥PA+AQ+AK-PA=AQ+AK.

“=”当且仅当α=β时成立，由α=β可知此时点P在AT上，所以，AT上任意一点均为最优点.

(3)当∠FOM>60°时，设∠AOF=α，∠AOM=β，∠POA=θ(θ

因为α+β=∠FOM∈(60°,90°)，

所以α、β中至少有一个不小于30°，

不妨设α≥β，所以α>30°，

下面对β进行分类加以证明：

①当β≥30°时,作点A关于EF和MN的对称点A′和A″，再分别过点A′和A″作MN和EF的垂线，垂足为H、G，过点P作OA的垂线，垂足为K(如图13所示).

图13

因为∠MOA′=2α+β>90°，所以垂足H在ON上，同理可证垂足G在OE上.此时，P点的最优点为点O，证明如下：

因为θ

S=PA+PB+PC

=PA+OP[sin(β+θ)+sin(α-θ)]

≥AK+OP[sin(β+θ)+sin(α-θ)].

因为α>30°，β≥30°，

所以S>AK+OP[sin(30°+θ)+sin(30°-θ)]

=AK+OPcosθ=OA.

所以O点为最优点.

② 当β<30°时，如果∠FOA″=α+2β≥90°，即过A″作EF的垂线，垂足为G在OE上.过点P作OA的垂线，垂足为K(如图14所示).

图14

(i)当点P在∠AOF内部(如图14所示)时，

由α+2β≥90°⟹α≥90°-2β

⟹90°>α-θ≥90°-2β-θ>0

⟹sin(α-θ)≥sin(90°-2β-θ)

⟹sin(α-θ)≥cos(2β+θ)，

S=PA+PB+PC=PA+OP[sin(β+θ)+sin(α-θ)]

>AK+OP[sin(β+θ)+cos(2β+θ)]

=AK+OP[sin(β+θ)+cos(2β+θ)-cosθ+cosθ]

=AK+OP[sin(β+θ)-2sinβsin(β+θ)+cosθ]

=AK+OP[sin(β+θ)(1-2sinβ)+cosθ].

因为β<30°，θ

所以sin(β+θ)(1-2sinβ)+cosθ>cosθ，

所以S>AK+OP[sin(β+θ)(1-2sinβ)+cosθ]

>AK+OPcosθ=AK+OK=OA.

(ii)当点P在∠AOM内部(如图15所示)时，

图15

由α+2β≥90°⟹α≥90°-2β

⟹90°>α+θ≥90°-2β+θ>0

⟹sin(α+θ)≥sin(90°-2β+θ)

⟹sin(α+θ)≥cos(2β-θ)，

S=PA+PB+PC=PA+OP[sin(β-θ)+sin(α+θ)]

>AK+OP[sin(β-θ)+cos(2β-θ)]

=AK+OP[sin(β-θ)+cos(2β-θ)-cosθ+cosθ]

=AK+OP[sin(β-θ)-2sinβsin(β-θ)+cosθ]

=AK+OP[sin(β-θ)(1-2sinβ)+cosθ].

因为β<30°，θ

所以sin(β-θ)(1-2sinβ)+cosθ>cosθ，

所以S>AK+OP[sin(β-θ)(1-2sinβ)+cosθ]

>AK+OPcosθ=AK+OK=OA.

③当β<30°时，如果∠FOA″=α+2β<90°即过A″作EF的垂线，垂足为G在OF的上.设A″G与MN交点为P0,则点P0为最优点.证明如下:

过点P0作PC的垂线，垂足为R(如图16所示).

图16

设∠AP0R=α′，∠AP0M=β′，∠AP0P=θ′，

因为α′+β′=∠AP0R+∠AP0M

=∠MP0R=∠MOF>60°，

故α′、β′中至少有一个大于30°，不妨设α′>30°.

又因为α′+2β′=90°，所以β′<30°；

由α′+2β′=90°⟹α′+θ′=90°-2β′+θ′

⟹sin(α′+θ′)=sin(90°-2β′+θ′)

⟹sin(α′+θ′)=cos(2β′-θ′)，

所以PA+PB+PR

=PA+P0P[sin(β′-θ′)+sin(α′+θ′)]

=PA+P0P[sin(β′-θ′)+cos(2β′-θ′)]

=PA+P0P[sin(β′-θ′)+cos(2β′-θ′)-cosθ′+cosθ′]

=PA+P0P[sin(β′-θ′)-2sin(β′-θ′)sinβ′+cosθ′]

=PA+P0P[sin(β′-θ′)(1-2sinβ′)+cosθ′]

>PA+P0Pcosθ′=P0A=P0A″,

即PA+PB+PR>P0A″，

所以S=PA+PB+PC

=PA+PB+PR+RC>P0A″+P0G

=A″G，

所以点P0为最优点.