纳米硅薄膜厚度对其反射与吸收性能的影响
2020-04-03蒋旭苏未安殷超
蒋旭, 苏未安, 殷超
(江西理工大学理学院,江西 赣州 341000)
0 引 言
纳米材料一般指组成相或晶粒尺寸小于100 nm的材料,因其独特的结构和优异的性能受到了广泛的关注[1-3]。 近几十年来,纳米材料与技术在生物技术、航天航空、工程材料、医学与健康、环境和能源等领域广泛使用,具有巨大的应用市场[4-9]。 其中,纳米硅薄膜因其用料少、成本低的优势和具有高电导率、可调控的光学能隙、表面与界面效应等特性[10-12],在薄膜太阳能电池、异质结二极管、量子功能器件、薄膜敏感器件、集成电路器件等新型光电器件[13-15]中具有广泛的运用前景。 纳米硅薄膜由纳米硅与界面结构组成, 可通过化学气相沉积(CVD)与物理气相沉积(PVD)制备,其中等离子体增强化学气相沉积法(PECVD)技术成熟,运用广泛[16-17]。 近年来,已经有大量关于纳米硅薄膜的制备、运用及其性质的研究[18-20],然而纳米材料的光学性质复杂多变,随着材料的薄膜化与纳米化,纳米硅薄膜的光学性能随之改变,其光反射与吸收性能也将受到薄膜厚度的影响,光学性能的不稳定性限制了纳米硅薄膜在光电器件方面的应用。因此系统的研究纳米硅薄膜光学性质有利于纳米硅薄膜光电器件的开发。
文中采用FDTD Solutions 对纳米硅薄膜的光电子特性进行完整的仿真。 FDTD 方法提供各种类型的材料模型、入射激励源及边界条件,能够设计各种复杂模型,实现高效的仿真建模,可有效地应用于宽光谱微纳光学仿真。文中系统地研究了纳米硅薄膜的光学性质,并对其反射率、吸收率和透射率随入射光波长与薄膜厚度的变化情况进行了详细的讨论,获得了与标准太阳光谱[21](AM1.5)匹配最佳的纳米硅薄膜厚度。
1 方法与模型
文中运用FDTD Solutions 对纳米Si 薄膜进行电磁场数值仿真与计算。 该方法借助电磁波理论,结合边界条件与电磁场参数, 求解麦克斯韦方程(Maxwell’s Equations)边值问题。 在求解边值问题时, 采用时域有限差分法 (Finite Difference Time Domain, FDTD)在时间域与空间域进行差分离散处理, 最后运算获取纳米Si 薄膜的电磁场分布及数值解。
对纳米Si 薄膜进行建模仿真,模拟模型如图1所示,纳米Si 薄膜放置于SiO2衬底上,薄膜表面为Air 层。 考虑到AM1.5 太阳光谱分布与薄膜硅的吸收波限,入射光波长范围选择400~1100 nm,垂直入射到纳米Si 薄膜上表面,电场沿x 轴方向偏振。2 个功率与频率监视器分别位于硅薄膜的表面和底部,3 个时间监视器分布于Air 层、 纳米Si 薄膜层与SiO2衬底层中。 仿真计算模型的上边界和下边界采用完全匹配层(Perfect matched layer,PML)[22]吸收边界,PML 吸收边界可吸收透射场与反射场,考虑到薄膜的周期性结构,x 轴和y 轴方向设置为周期性边界。

图1 纳米硅薄膜仿真模型
2 结果与分析
2.1 垂直入射光在纳米硅薄膜中的衰减
根据图1 的仿真模型所示,持续照射时间约为10 fs,其电场强度沿x 轴,磁场强度沿y 轴,能流密度沿z 轴方向;纳米Si 薄膜的厚度为500 nm。由时间监视器可获得Air 层、 纳米Si 薄膜层以及SiO2衬底层中的电场实部Re(E)、磁场实部Re(H)与能流密度P(P=E×H),其结果如图2 所示。

图2 电场、磁场与能流密度在各层中的衰减情况
由图2(a)、(b)、(c)可知,Air 层中的电场、磁场与能流密度为类似脉冲波,其幅度先增加然后衰减变小, 脉冲时间为10 fs 左右。 脉冲停止约5 fs后,Air 层中的电场、磁场与能流密度又出现微弱的脉冲波。 根据计算可知,这是由于入射光在Si 薄膜层的表面发生反射而再次进入Air 层所导致的结果。 由图2(d)、图2(f)可知,纳米Si 薄膜层中的电场与能流密度的振幅相较于Air 层有显著的减小,这说明纳米Si 薄膜层对入射光存在显著的吸收。纳米Si 薄膜存在本征吸收、激子吸收、晶格振动吸收与自由载流子吸收等多种形式的吸收,其吸收系数约为105cm-1。 其中只有本征吸收能够形成光电导,直接产生非平衡载流子,引起光电效应。激子吸收、晶格振动吸收与自由载流子吸收等吸收不能形成光电导,而引起光热效应[23-24]。 由图2(e)可知,纳米Si 薄膜层中的磁场却与Air 层的差别不大,表明光在与物质相互作用时, 磁场的作用不明显。 由图2(g)~图2(i)可知,SiO2衬底层和Si 层中的电场振幅差别较小, 表明SiO2衬底层对该波段范围的光子吸收微弱。此外,SiO2衬底层中的电场、磁场和能流密度随时间的衰减情况表明入射光在纳米Si 薄膜中产生了法布里-珀罗干涉效应[25-26]。
分析可知,对于纳米硅薄膜半导体材料,自由电子和束缚电子对材料的吸收都具有重要的意义,材料的吸收系数决定于电导率。电磁波衰减情况表明该模型的纳米Si 薄膜层结构对入射的电磁波存在明显的吸收现象,通过入射光电场、磁场与能流密度随时间衰减变化的情况可以看出吸收的时间极短。
2.2 纳米硅薄膜光学性质随厚度变化
根据如图1 所示的仿真模型,使用波长400~1100 nm 的平面波,模拟仿真了厚度从10~800 nm不同纳米Si 薄膜的反射、透射与吸收情况。 其中,反射率通过纳米Si 薄膜层上方Air 层中的功率与频率监视器获得,图3(a)给出了不同厚度d 的纳米Si 薄膜反射率R 随波长λ 的变化情况。
由图3(a)可知,纳米Si 薄膜反射率的变化趋势大体可以分为I、II 两个区域。区域I 为较短波长(λ~400-500 nm) 的光入射到较厚的纳米Si 薄膜(d>200 nm)时,入射光的波长和薄膜的厚度对其反射率的影响不明显,其反射率R 在0.4 附近有微小的波动。而在区域II,纳米Si 薄膜的反射率R 受入射光波长和薄膜厚度的影响较大,且反射率出现了明暗相间的条纹结构, 最大的反射率Rmax高达0.8,而最小的反射率Rmin仅为0.05,这一现象主要是由于薄膜之间的法布里-珀罗干涉而导致的。
当光强为I0的光波垂直入射到厚度为d 的理想薄膜上表面时, 此时不考虑薄膜内的吸收作用,入射光将在薄膜表面发生反射和透射现象,透射光在薄膜下表面再次发生反射。上下表面的反射光波相遇时将产生干涉效应,其相干光强I 与入射光的光强I0的比值(即归一化的相干光强)满足[27]:

图3(b)给出了波长λ 为400~1100 nm 的光波入射到厚度d 为10~800 nm 的理想薄膜, 其反射光强I 的变化情况。由图3(b)可见,薄膜干涉使得反射光强出现了明暗相间的条纹结构,且与图3(a)中区域II 的条纹结构一致。 这表明当光波入射到纳米Si 薄膜时,其薄膜干涉效应显著,不可忽略。 而对于区域I,图3(a)与图3(b)的结果有非常大的差异, 纳米Si 薄膜中的反射率R 的干涉条纹现象不明显,而图3(b)中出现非常明显的明暗干涉条纹。其主要原因是由于纳米Si 薄膜对短波段高能量的光子具有较高的吸收,从而使得下表面的反射光与上表面的反射光相遇时两光束强度差异较大,干涉效果较弱。对于区域II,图3(a)与图3(b)中的条纹间距与条纹形状也存在差异。 纳米Si 薄膜与理想纳米硅薄膜的图像相比,其条纹间距较宽,随着波长和厚度的增加而变大, 且条纹形状更为平缓,这是由于硅材料的薄膜化与纳米化使得Si 薄膜的电导率变高、光学能隙宽化等[28-30]因素导致的结果,这说明薄膜化与纳米化对Si 薄膜的性质有显著的影响。

图4 纳米硅薄膜透射率与吸收率随入射光波长λ 与薄膜厚度d 的变化关系
图4 给出了纳米Si 薄膜的透过率T 和吸收率A 随入射光波长λ 与薄膜厚度d 变化情况。透过率T 由SiO2衬底层中的功率与频率监视器获得,而吸收率A 根据能量守恒关系(A=1-T-R)计算得到。由图4(a)、图4(b)可见,纳米Si 薄膜的透射率与吸收率的变化趋势也可以分为I、II 两个区域,这与纳米Si 薄膜中反射率的变化规律相一致。
在区域I,纳米Si 薄膜的透射率T 较低,其值在0.12 左右有微小的变化(见图4(a)),而吸收率较高,其值在0.57 附近变化(见图4(b))。 纳米Si薄膜的吸收系数α(α=4 kπ/λ)在短波时的吸收系数达到106cm-1, 入射光子在很短的距离内就被纳米Si 薄膜吸收[31],因而,此时薄膜厚度对其吸收率影响不大。 对于区域II,由于入射光波长越大,其穿透性越强,透射率越高,并且由于法布里-珀罗干涉效应, 透射率呈现出明暗相间的条纹结构,其最大值Tmax高达0.99,最小值Tmin达到0.24(见图4(a)),而对于区域II 的吸收率,当波长较小时,吸收率呈现出明暗相间的条纹结构,其最大值Amax高达0.62,最小值Amin为0.12。 当波长较大时,由于光子能量较低,吸收系数较小,此时吸收率A 较小,其值在0.06 附近有微小的波动(见图4(b))。 在波长λ 为400~1100 nm 范围内的区域I 与区域II,受薄膜反射率的影响, 纳米Si 薄膜的透射和吸收都随波长大小与薄膜厚度的改变同样产生明暗相间的条纹。
为了探讨薄膜化与纳米化对硅材料性能的影响,进一步研究了体硅的反射率R、透射率T 与吸收率A 随波长(λ~400-1100 nm)的变化情况。 研究仍然采用FDTD 方法模拟计算了半无限型体材硅[32]的反射率R、透射率T 与吸收率A,其结果如图5 所示。 在计算的过程中,将硅层厚度设置为半无限型,通过调整功率与频率监视器位置而获得硅材料中不同深度h(10~800 nm)处的透射率T 与吸收率A。
如图5(a)所示,与纳米Si 薄膜相比,半无限硅不受薄膜干涉的影响, 其反射率仅与波长大小相关, 入射光波长越大, 穿透性越强, 在波长λ 为400~1100 nm 的范围内,反射率R 随波长的增大而减小。 由图5(b)、图5(c)可知,理想的半无限硅透射率、 吸收率与纳米Si 薄膜相似, 入射光波长为400~500 nm 时,硅吸收层的吸收系数较大,透射率都随厚度的增加而减小,吸收率随厚度的增加而增加强。 波长为500~1100 nm 时,硅吸收层的吸收系数较小,透射率相对较大,吸收率相对较小。在波长λ 为400~1100 nm 的范围内,与纳米Si 薄膜相比,半无限硅不受薄膜干涉的影响,透射和吸收随波长大小与薄膜厚度的改变将不会产生明暗相间的条纹, 其中透射率随波长与厚度的增加而平缓地增加,而吸收率随波长与厚度的增加而平缓地减小。

图5 半无限硅的反射率、透射率与吸收率随波长λ 与深度h 的变化关系
对比纳米Si 薄膜和半无限硅材料中的模拟结果(图3(a)、图4 与图5)可知,纳米Si 薄膜的透射率与吸收率的I、II 两区域的分界与半无限硅中相应的变化趋势相一致,但其光学性质与半无限硅中的变化规律却有显著的差异, 纳米Si 薄膜的透射率和吸收率随波长和厚度的变化出现了明暗相间的条纹结构,而半无限硅中则呈现出平滑的变化趋势。实验结果显著地体现了薄膜干涉效应等特性在纳米硅薄膜中的影响,这表明薄膜化与纳米化对材料的性能具有较大的影响作用。
2.3 纳米硅薄膜厚度的选择
纳米Si 薄膜在光电器件方面的应用中, 一般需要选择最佳的吸收效率,同时还需要兼顾材料的成本。 根据上面的模拟结果(图4(b)与图5(c))可知, 当薄膜厚度达到500 nm 时, 具有较高的吸收率,而继续增加其厚度,会提升材料的成本,且吸收率的增加变得缓慢。
当硅层厚度为500 nm 时,纳米Si 薄膜与半无限硅的吸收率A 随波长λ 的变化如图6 所示,半无限硅的吸收率随着波长的增大呈现出先增大后变小的趋势,当入射光波长为400 nm 时,其吸收率为0.54,在波长为417 nm 时取得最大吸收率0.55,而当波长增大到1100 nm 时,吸收率仅为0.01。 纳米Si 薄膜的吸收率随波长的变化呈现出波动,入射光波长为400 nm 时,其吸收率为0.54,薄膜吸收率波动较大, 在波长为461 nm 时取得最大吸收率0.61,而当波长为1100 nm 时,吸收率仅为0.02。 由图6 可见, 半无限硅的吸收率随波长的变化平缓,而受薄膜干涉性质的影响, 纳米Si 薄膜吸收率随波长变化呈现出巨大的波动现象。 通过比较可知,相较于半无限硅, 纳米Si 薄膜的吸收效率被显著增强,这归功于纳米Si 薄膜中薄膜干涉效应、表面与界面效应与光学能隙宽化等特性对其性质的影响。 这表明在开发新一代薄膜型光电器件方面,厚度为500 nm 的纳米Si 薄膜是较佳的选择,这与当前的研究结果与运用[33-35]相一致。
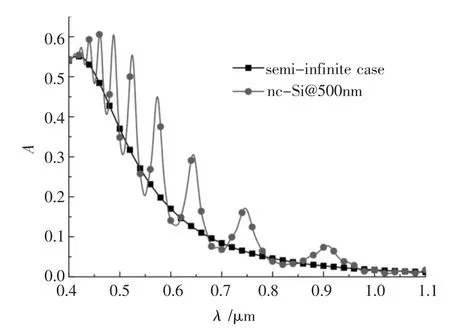
图6 500 nm 的纳米硅薄膜与半无限硅吸收率A 随波长λ 变化的情况
3 结 论
在本文中,通过FDTD solutions 采用时域有限差分对纳米硅薄膜进行了模拟仿真与计算,研究了纳米硅薄膜对入射电磁波的衰减作用,分析了纳米硅薄膜的厚度对其光学性质的影响。 研究表明,相较于Air 层与SiO2衬底层,纳米硅薄膜对入射电磁波存在显著地吸收作用,且吸收时间极短。 纳米硅薄膜的反射率与吸收率受薄膜厚度与入射光波长的影响,在短波段的反射率较低,而吸收率较大,当薄膜厚度大于500 nm 时,其最大吸收率可达0.62,受薄膜干涉作用的影响, 长波段的反射率波动较大,最高反射率达到0.80,而最小反射率仅为0.05。通过对比纳米硅薄膜与半无限硅的反射与吸收特性可知,纳米硅薄膜与半无限硅的光吸收都集中于波长λ 为400~600 nm 的短波段区域,而长波段吸收较弱。 受硅材料薄膜化与纳米化的影响,纳米硅薄膜具有光学能隙宽化、高电导率等特性,吸收效率显著增强。当硅薄膜厚度为500 nm 时,具有较高的吸收效率且材料使用少、成本低,可运用于纳米硅薄膜光电器件。通过对纳米硅薄膜反射与吸收性能的系统研究,可为纳米硅薄膜在光电子器件的运用提供依据,有利于开发高效的纳米硅薄膜光电子器件。
