面向属性概念的属性粒构建

吴克晴, 陈希邦

（江西理工大学理学院，江西 赣州341000）

0 引 言

粒计算(Granular Computing,GrC)首先由Zadeh教授[1]提出。 粒计算是通过信息粒化过程将复杂的问题进行分解、 转化得到多个相对简单的子问题，然后再对这些简单的子问题进行处理，从而实现对复杂问题的求解[2]。粒计算的基础是信息粒化，即在给定的粒化准则下，粒化的过程是通过对问题空间的划分产生多个信息粒，这些粒可以用来描述问题本身所包含的一些信息，粒之间的偏序关系就形成了多层次的粒结构。 粒计算的思想应用于各种领域，如结构化问题的求解、结构化信息处理等[3-4]。

形式概念分析[5]与粗糙集[6]在1982 年同时被提出， 许多学者都认为它们是很有效的粒计算的方法，并且两者之间有着极强的互补性。

形式概念分析[5]这一理论是由德国数学家Wille R教授提出， 国内的研究学者通常称之为概念格理论。 概念格理论多用于知识发现以及知识表征，通过知识本身的外延和内涵之间的依赖或者因果关系，通过构建Hasse 图来建立概念层次结构。 概念格理论经过多年的研究探索，已经逐渐形成了一些具有特色的研究方向，比如概念格属性约简[7]、三支概念分析[8]等。目前，在人工智能、机器学习、信息检索等领域，概念格理论均有较为广泛的应用，同时与粗糙集、模糊集、数据挖掘等理论具有很好的结合性[9]。 而粗糙集作为一种处理不确定性问题的数学工具，特别是在人工智能领域中作为一个较新的学术热点，在机器学习、知识获取、决策分析、过程控制等许多领域得到了广泛的应用[10-11]。

研究人员通过粒计算与形式概念分析以及粗糙集的结合，得到一系列成果，如粒规则获取[12]、三支粒约简[13]、多粒度概念格的构建[14]等。王一宾等[15]研究了基于对象导出三支概念格的规则提取。 Ma等[16]通过讨论分层扩展集的性质，提出了一种快速构造面向对象概念格的算法。 李金海等[17]利用经典形式背景给出多粒度标记形式背景的定义，证明了多粒度标记形式背景与多粒度标记信息系统在语义上等价。Zhi 等[18]基于必要的属性分析，从不完整的形式语境中探讨知识发现，提出了一种新的知识发现粒度描述方法。 文献[19]通过使用缩放算法，可以通过现有的属性（对象）导向概念格直接生成基于不同属性粒度的属性（对象）导向概念格。 文献[20]基于形式概念分析中粒的思想和粗糙集理论中上、 下近似的方法通过对必然属性分析的粒描述进行了研究， 定义了一元可定义粒以及二元可定义粒。

文献[20]主要通过面向对象概念格的角度对其进行了研究，而在研究中，作者并没有从面向属性概念角度进行研究，因此，文中在文献[20]的基础上进一步扩展，首先是对属性粒的描述，然后给出一元可定义属性粒、一元属性描述子的描述、二元可定义属性粒、二元属性描述子的描述，最后通过对比验证可以证明其有效性。

1 基本概念

为了本文内容的完整性以及便于读者的阅读，本节主要是介绍文中所提到的一些基本概念。

1.1 形式概念分析与概念格

定义1（G，M，I）为形式背景，对象拥有的属性所构成的集合为g*={m∈M|gIm}，同样的，属性m所对应的对象的集合为m*={g∈G|gIm}。 其规则详见文献[21]中的定义1.6。

定义2[21]设（G，M，I）为形式背景，其中A⊆G，B⊆M，定义：

定义3[21]设（G，M，I）为形式背景，A⊆G，B⊆M。 有A□=B 且B◇=A，则称序对（A，B）为面向对象概念；若A◇=B 且B□=A，则称序对（A，B）为面向属性概念。

本文主要通过对面向属性概念的研究， 称A为面向属性概念（A，B）的外延，B 为面向属性概念（A，B）的内涵，在不产生歧义的情况下，统称A 为外延，B 为内涵[21]。

定义4[21]设C1=（A1，B1），C2=（A2，B2）是形式背景K=（G，M，I）上的两个面向属性概念，若存在A1⊆A2，则有C1≤C2，称关系≤是概念的“层次序”，（简称“序”）；如果不存在概念（A3，B3）使得A1⊂A3⊂A2， 则称C1是C2的直接子概念，C2是C1的直接父概念，记做C1＜C2。K=（G，M，I）的所有面向属性概念用这种序组成的集合称为面向属性概念格，记做LA=（G，M，I）。

1.2 面向属性概念格的构建

本小节主要从粗糙集中的下近似角度出发，通过使用“*”算子，来构建面向属性概念格[22]。

例1 一 个 形 式 背 景K=（G，M，I），G={1 ，2，3，4，5}，M={a，b，c，d，e，f}，其G 与M 之间的关系如表1 所示。

算法1 由下近似出发，构建面向属性概念格：

Step1：分别计算g＊i，其中gi∈G；

表1 形式背景

Step2：计算P（M）中的元素；

Step3：逐一判断P（M）中的每一个元素是否满足g＊i⊆B 且g＊i⊆B，其中B⊆M，若满足，则（∪gi，B）为一个面向属性概念；否则（∪gi，B）舍去；

Step4：将Step3 中得到的所有概念按照对象外延的包含关系顺次连接， 从而得到概念格LA=（G，M，I）。

根据上述算法，对例1 所示的形式背景可以通过下近似构建其面向属性概念格，如图1 所示。

图1 例1 形式背景的面向属性概念格

1.3 粒的描述

粒计算作为一种新兴的计算方法，它为相关研究领域提供了基于信息粒化来解决复杂问题的理论框架，是当前计算机领域中解决复杂问题和核心技术之一。 近几年来，许多研究学者通过粒计算的理论知识来研究知识发现领域的一些问题。

定义一个论域G， 所有可能的粒组成G 的幂集，记做2G，论域G 的属性集用M 表示，即G 与M之间的二元关系由I：G×M 来表示，因此，一个形式背景K=（G，M，I）可以用来描述一个论域[19]。

同理，定义一个属性论域M，M 中所有可能的粒组成的幂集，记做2M，与属性集对应的对象集用论域G 表示，其二元关系同样可以有I：G×M。

定义5[23]一个形式背景K=（G，M，I），设B 为论域G 中对象的属性的集合， 其B1，B2，B3， …，Bn中是B 的子集，则称是论域G 上的属性粒。

定义6 给定一个粒B⊆2M以及一个对象集A⊆G，则若对任意的g∈A，都有g*⊆B，则对象集A 必然具有属性粒B。

属性粒的大小表示该粒所包含的信息量的度量，属性粒越小则说明信息量越小，反之亦然。

2 一元属性描述子的粒描述

本小节主要研究基于一元属性描述子的属性粒描述，定义了正文字可定义属性粒和负文字可定义属性粒，它们统称为一元可定义属性粒，并将对它的描述称为一元属性描述子。

2.1 正文字可定义属性粒的描述

文献[20]中提出了正文字可定义粒并对其性质进行了分析，本节从面向属性概念格角度探索性的定义了正文字可定义属性粒。

定义7 一个形式背景K=（G，M，I），B⊆2M，若存在一个面向属性概念C∈L（K），有C 的内涵为B，则B 称为一个正文字可定义属性粒。

在形式概念分析中，文献[20]采用最小产生子来表达一个概念的核心属性，类似地，本文定义最小对象产生子来表达一个概念的核心对象。

定义8 一个净化的面向属性概念C=（A，B），设X⊆A，有X◇=A◇=B，且对于任意的S⊂X，有S◇⊆A◇，则称X 是概念C 的一个最小对象产生子。

对于最小对象产生子的方法与文献[20]中最小产生子的方法类似，这里则不进一步描述。

对例1 所示的形式背景，它的正文字可定义属性粒及其最小对象产生子如表2 所示。

表2 正文字可定义属性粒及其最小对象产生子

2.2 负文字可定义属性粒的描述

对于面向属性概念格， 有正文字可定义属性粒，就会存在负文字可定义属性粒，而负文字可定义属性粒是针对形式背景的补背景而言的。 对例1的形式背景K=（G，M，I），G＝{1，2，3，4，5}，M＝{a，b，c，d，e，f}，其补背景Kc=（G，M，Ic）如表3 所示。

表3 形式背景的补背景

表3 的形式背景Kc的面向属性概念格如图2所示。

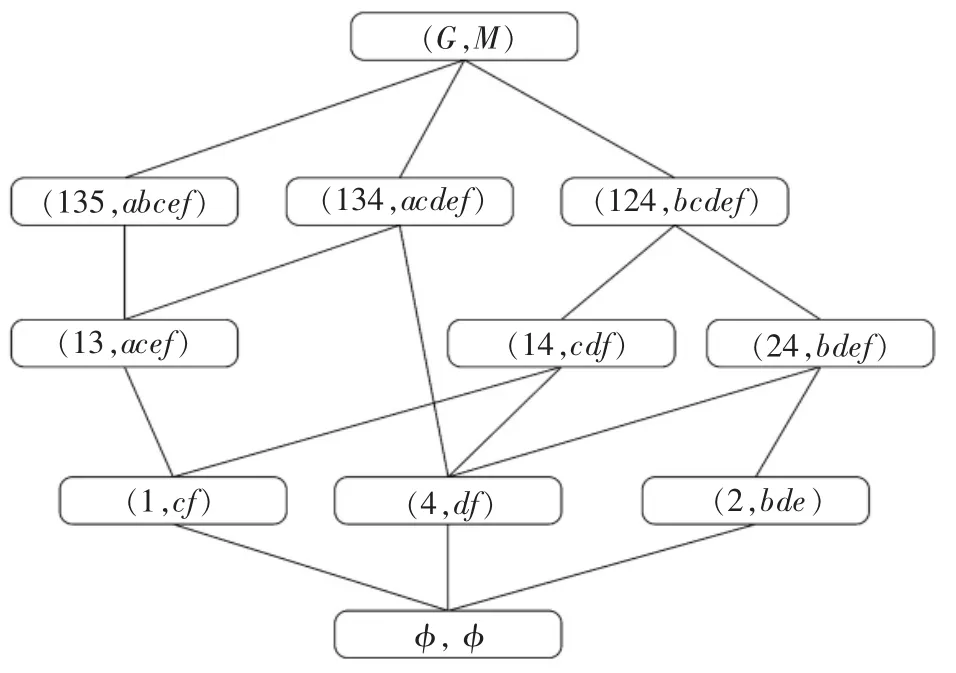
图2 面向属性概念格L（Kc）

在形式背景Kc中，根据形式背景K 定义正文字可定义属性粒及最小对象产生子的方法，可以得到负文字可定义属性粒及其最小对象产生子，如表4 所示。

表4 负文字可定义属性粒及其最小对象产生子

2.3 一元不可定义属性粒的描述

在一个形式背景中，正文字可定义属性粒与负文字可定义属性粒统称一元可定义属性粒， 此外，若该粒不是一元可定义属性粒，则称为一元不可定义属性粒。

下面给出基于一元属性描述子的近似描述精度。

一个形式背景K=（G，M，I），mA是一元可定义属性粒的集合，B⊆2M是一个一元不可定义属性粒， 若∃Bl，Bu⊆mA， 有Bl⊂B⊂Bu， 且不存在Bl*，Bu*⊆mA，使得Bl⊂Bl*⊂B⊂Bu*⊂Bu，则称Bl，Bu分别为B 的A-下近似属性粒和A-上近似属性粒，且B 的A-近似描述为dA（B）=[d（Bl），d（Bu）]，其中，d（Bl）和d（Bu）分别为B 的A-下近似和A-上近似的最小产生子，B 的A-近似精度为

3 二元属性描述子的粒描述

上一节中主要通过定义正文字可定义属性粒和负文字可定义属性粒，以及探索面向属性概念的最小产生子来对属性粒进行描述。在对属性粒的描述中，为了提高其精度，需要同时用到原形式背景以及其补背景所包含的信息，因此，本节将提出基于二元属性描述子的二元可定义属性粒，并提出基于二元可定义属性粒的M-三支概念格及其构建算法。

定义9定义一个形式背景K=（G，M，I），其中U，V⊆G，B⊆M，若（U，V）□=B，且B◇=（U，V），称（（U，V），B）为属性诱导的三支概念，简称M-三支概念，其中（U，V）为M-三支概念的外延。

这里对由对象诱导的三支概念不做赘述。

在上述定义中的形式背景中，U 描述了拥有属性A 的对象集，V 描述了不拥有属性A 的对象集，G-U-V 描述了拥有其他情况。

M-三支概念之间的偏序关系可以定义为：（（U1，V1），B1）≤（（U2，V2），B2）⇔B1≤B2，则 称 形 式背景的所有M-三支概念满足偏序关系≤构成一个完备格，记为属性诱导的三支概念格，简称M-三支概念格，记做LM（K）。

3.1 二元可定义属性粒的描述

定义10定义一个形式背景K=（G，M，I），B⊆2M，若存在M-三支概念（（U，V），B）∈LM（K），则称B 为二元可定义属性粒，（U，V）为二元对象描述子。

定义11一个M-三支概念C=（（U，V），B）∈LM（K），设（u，v）⊆（U，V），有（u，v）◇=（U，V）◇=B，且对于任意的（u1，v1）⊂（U，V），有（u1，v1）◇⊆（U，V）◇，则称（u，v）是概念C 的一个最小对象产生子。

类似于3.2 和3.3 小节的讨论， 对于例1 中的形式背景，可以得到该形式背景所对应的M-三支概念格以及二元可定义属性粒和最小产生子。

3.2 算法描述

对于M-三支概念格的构造算法，主要分为两个部分，一是构造混合形式背景KM，二是对混合形式背景构建其概念格，具体步骤如下：

算法2

Step1：输入形式背景K=（G，M，I）；

Step2：计算补背景Kc=（G，M，Ic）；

Step3：将K，Kc按照对象集叠置，得到混合形式背景

Step4：分别计算（gi，gj）*，其中（gi，gj）*∈GM；

Step5：计算P=（M）中的元素；

Step6：逐一判断P=（M）中的每个元素是否满足（gi，gj）*⊆B 且（gi，gj）*＝B，其中B⊆M，若满足（∪（gi，gj）*，B）则为一个三支概念；否则（∪（gi，gj）*，B）舍去；

Step7： 将step 3 中得到的所有概念按照对象外延的包含关系顺次连接，从而得到概念格L=（G，M，I），如图3 所示。

该形式背景所对应的M-三支概念、二元可定义属性粒和最小产生子如表5 所示。

3.3 二元不可定义属性粒的描述

类似一元不可定义属性粒， 二元不可定义属性粒指的是不存在M-三支概念（（U，V），B）∈LM（K），则B 为二元不可定义属性粒。

下面给出基于二元属性描述子的近似描述精度。

一个形式背景K=（G，M，I），mD是一元可定义属性粒的集合，B⊆2M是一个二元不可定义属性粒， 若∃Bl，Bu⊆mD， 有Bl⊂B⊂Bu， 且不存在Bl*，Bu*⊆mD，使得Bl⊂Bl*⊂B⊂Bu*⊂Bu，则称Bl，Bu分别为B 的D-下近似属性粒和D-上近似属性粒， 且B的D-近似描述为dD（B）=[d（Bl），d（Bu）]，其中，d（Bl）和d（Bu）分别为的D-下近似和D-上近似的最小产生子，B 的D-近似精度为:

4 对比验证

4.1 三种近似描述的对比验证

图3 M-三支概念格

表5 二元可定义属性粒及其最小对象产生子

文献[20]结合粗糙可定义粒、一元可定义粒以及二元可定义粒来讨论粒的描述精度问题，本文提出了一元可定义属性粒、二元可定义属性粒，并分别基于一元可定义属性粒和二元可定义属性粒讨论了粒的近似描述问题。下面从描述精度角度对这三种近似描述方法进行比较研究。

为了统一描述，全体粗糙可定义属性粒组成的集合记做gR，给定一个属性粒B，基于粗糙可定义属性粒的上近似和下近似可定义为R-上近似和R-下近似，其近似描述记做R-近似描述，记做dR（B），描述精度记做ρR（B）。

设一个形式背景K=（G，M，I）， 粗糙可定义属性粒的全体mR、 一元可定义属性粒的全体mA、二元可定义属性粒的全体mD有mR⊂mA⊂mD，描述精度满足ρR（B）≤ρA（B）≤ρD（B）。在此需要说明的是，每一个近似描述对应着一个近似描述精度，由于某一属性粒的近似描述可能存在多种情况，为保证描述精度的唯一性，可取最大的近似描述为该属性粒的最佳近似描述。

对于例1 中的形式背景， 取B={b，c，d}， 则有R-下近似为{b，d}，R-上近似为{a，b，c，d，f}，属性粒B 的R-近似描述dR（B）=[d（Bl），d（Bu）]=[d{b，d}，d{a，b，c，d，f}]=[3，2∨3]， 即R-描述精度为ρR（B）=同理，根据2.3 小节和3.3 小节中的两种近似描述可得，属性粒B 的A-近似描述dA（B）=[d（Bl），d（Bu）]=[d{b，d}，d{a，b，c，d，f}]=[3，2∨3]，由公式（5）可得，A-描述精度ρA（B）=0.4，满足ρR（B）≤ρA（B），属性粒B 的D-近似描述dD（B）=[d（Bl），d（Bu）]=[d{b，d}，d{b，c，d，f}]=[3，2∨┒1]，由公式（6）可得，D-描述精度ρD（B）=0.5，满足ρA（B）≤ρD（B），即可证实ρR（B）≤ρA（B）≤ρD（B）成立。实际上，对于∀B∈2M，均可证明ρR（B）≤ρA（B）≤ρD（B）成立。

4.2 与其他知识获取方法的对比

通过构建属性粒，并对其进行近似描述，在对形式概念描述的同时， 不可定义属性集的描述问题得以解决， 与概念格中只对形式概念进行描述的研究相比， 本文对不可定义属性集的描述则是对与模糊集理论来说， 对挖掘更多的知识提供了可能性。

人们获取知识的途径有很多种，为了凸显本文研究与其他方法的异同，本文选择了几种较为典型的知识挖掘方法进行对比，具体如表6 所示。 可以看出，文本表征法是单一的文本表示，虽然成熟全面但已经不适应当今知识获取的途径，超文本表征法是文本从静态到动态的新形态， 但其操作复杂，与用户的交互性较差；FCA 表示法即用建格的方式直观的表征信息， 具有层级性和交叉连接的特征；粒描述表示法也是本文的方法，在FCA 表示法的基础上，通过粒化、构建属性粒的方式来处理形式背景，在获取形式概念的知识的同时，对非形式概念的知识也有了表示的方法，即通过近似描述的方式可以获取更全面的知识。

表6 知识挖掘的方法对比

5 结 论

粒计算是目前大数据方向最有效的解决问题的方法之一，粒计算与形式概念分析理论的结合使得知识发现的过程更细致化，能够更好的令读者学习以及理解知识发现过程，本文通过从面向属性概念格的内涵角度定义了一元可定义属性粒、二元可定义属性粒以及M-三支概念格的构造算法。 需要指出的是，文献[20]从概念格基于必然属性角度定义了一元描述子，二元描述子以及N-三支概念格，并对其进行了描述，本文不仅通过属性格角度对其进行了扩展，而且还对M-三支概念格的构造算法进行了描述，通过验证可证实研究的有效性，使得面向对象概念格和面向属性概念格与粒计算的结合更为丰富。

为了更好地实现通过面向属性概念格对属性粒的构建，还需要进一步的研究工作，主要包含：

1）面向属性概念格建造的属性粒会随着属性约简后变更，则变更后的动态更新问题需要进一步解决；

2）如何降低M-三支概念格构造算法的时间复杂度需要进一步思考。