一种复杂系统的分数阶内模PID 控制器设计
2020-04-03任金霞蒋梦倩黄艺培
任金霞, 蒋梦倩, 黄艺培
(江西理工大学电气工程与自动化学院,江西 赣州341000)
0 引 言
近年来随着工业发展以及计算机水平的提高,在很多领域中都开始运用分数阶微积分学理论,基于分数阶微积分的控制理论和应用分析越来越受到专家学者们的关注[1]。PIλDμ控制器相比传统整数阶控制器更具有灵活性,使得控制系统的控制效果更加理想,但分数阶控制器也在整定参数方面带来了难题。 近年来,大量学者在原有参数整定方法的基础上,结合先进控制技术以及优化算法设计分数阶控制器,如文献[2]基于改进的Oustaloup 方法,采用改进式遗传算法对控制参数进行整定;文献[3]使用改进的粒子群优化算法,对分数阶PID 控制器的参数进行离线优化;文献[4]采用RBF 神经网络控制算法, 对分数阶PID 控制器的积分阶次和微分阶次实时在线自整定;文献[5]通过模糊控制和免疫调节结合完成分数阶控制器的参数整定;文献[6]将滑模理论与分数阶理论相结合设计分数阶滑模控制器。研究实验表明,分数阶控制器具有很好的控制性能。
由于控制系统常常呈现高阶特性,若直接对高阶系统设计控制器工作量大, 实现难度系数高,其控制效果也不佳,因此通常需要先对模型进行降阶简化处理。 文献[7-8]针对高阶系统采用了不同的降阶方法得到降阶模型,逼近效果也高度近似。 内模控制方法具有设计直观、调节参数少、以及对模型要求精度低、抗干扰能力强等特点。 利用模型降阶降低复杂度,然后再将内模控制参数调节少等优点考虑到分数阶控制中,可减少控制器设计和参数整定的复杂问题,也能提高系统的控制性能。
文中采用混合粒子群优化算法对原高阶模型进行降阶处理, 然后在内模控制原理的基础上,完成分数阶内模控制器的设计,依据最大灵敏度法实现控制器的参数整定,最后通过仿真实例验证了方法的可行性,提高了对象的控制效果。
1 分数阶PID 控制器
分数阶微积分定义是由整数阶微积分定义发展而来,通常表示分数阶微积分的基本算子,连续的微积分算子常用表达式如下:
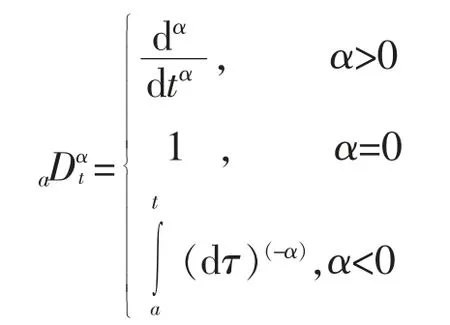
有关分数阶微积分的定义有以下3 种定义:R-L 定义、G-L 定义和Caputo 定义。 其中G-L 定义应用比较广泛,其表达式如下:
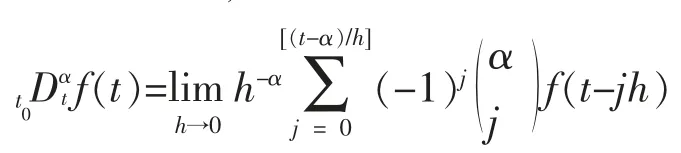
其中,[x]表示的整数部分;h 为计算步长。
一般分数阶控制器的传递函数如下:

其中,λ、μ 分别为控制器的积分和微分阶次。 从式中可看出整数阶控制器[9]是分数阶PIλDμ控制器积分和微分阶次均取值为1 时的特殊形式。典型的单位负反馈分数阶闭环系统的结构如图1 所示。

图1 分数阶控制器结构
2 基于混合粒子群算法的模型降阶
在模型降阶过程中,文中采用新型延迟分数阶模型,其近似模型如下:

其中,K 为增益;λ 为延迟系数;T 为时间常数;β 为任意实数,表示分数阶的系统阶次。
粒子群优化算法[10]主要特点是原理简单、参数少、较强的鲁棒性,已在多个领域得到了广泛的应用,但标准粒子群算法易陷入局部极小值。 本文采用混合粒子群算法对原复杂模型进行降阶,利用粒子群算法与遗传算法的思想[11-12]相结合,在粒子群算法中加入遗传算法中的交叉和变异步骤,让粒子实现交叉以及自身变异后寻找最优解,这样既避免粒子群算法陷入局部最优解同时又确保了收敛精度。 其混合算法流程表述如下:
1)选取适应度函数。适应度函数为原系统模型和降阶模型的单位阶跃响应误差:

其中,n 为搜索次数;y(t)和ym(t)分别为原系统模型和降阶模型。
2)确定搜索向量。模型搜索向量为θ=[K,λ,T,β]。
3)算法初始化。 随机产生粒子种群数M 值、迭代次数N 值、 学习因子c1和c2数值、 粒子的位置xid和速度vid值,另外采用实数编码方式。本文选取M=30,N=50,c1=c2=1.5。
4)根据适应度函数计算各粒子的适应度值,比较得出初始全局最优粒子。
5)更新粒子自身速度与位置。将其适应度分别与所经历的历史最佳值以及当前种群中最佳值进行比较,若优于它们,将其作为当前的最优位置进行替换。 其中速度更新和位置更新方程如下:

其中,pid和pgd分别为粒子当前所经历的最优位置和全局最优位置;r1和r2为[0,1]中均匀分布的随机数;ω 为惯性因子。 其惯性因子的计算公式如下:

其中,t 为当前迭代步数;tl为迭代最大步数。 本文选取ωl=0.9,ωd=0.4。
6)判断是否满足截止条件(足够好的解或最大迭代次数)。若没有,则跳到第(7)步执行,否则算法结束,输出最优结果。
7)利用整数交叉方式,新粒子是历史粒子同个体极值以及群体极值交叉而得到,个体内部采用互换方式对自身进行变异操作。 然后继续执行步骤(5)。
8)如果达到要求,退出;反之,继续执行步骤(7)。
3 基于内模控制的分数阶控制器设计
利用内模控制的思想:将模型与实际控制对象并联,然后控制器逼近模型的逆,其思想完全满足闭环系统的性能。 内模控制的基本结构如图2 所示,R(s)是设定值,Y(s)是系统的输出,D(s)是外来扰动,G(s)和M(s)分别是被控对象模型和等效被控对象模型,CM(s)是内模控制器。其等效内模控制反馈框图如图3 所示。

图2 内模控制框图

图3 内模控制等效反馈
在传统反馈控制中,反馈控制器Cc(s)由内模结构中CM(s)与M(s)结合而成:

内模控制中,将过程模型可分解为可逆M-(s)部分,不可逆M+(s)部分。 另外采用一阶泰勒级数逼近时滞环节可得:
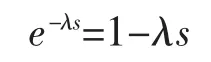
新型延迟分数阶模型分解如下:
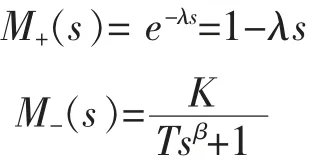
而内模控制器的传递函数表达式如下:

其中,f(s)是低通滤波器,其表达式如下:

其中,θ 为滤波器可变参数, 也是内模控制中唯一可调参数。
由以上的推理过程以及根据内模控制原理可得新型延迟分数阶反馈控制器的表达式:

4 分数阶PIλDμ 控制器参数整定
文中采用灵敏度法作为分析性能指标,灵敏度越小,系统跟踪误差也越小,对应的鲁棒稳定性也越好。 其定义式如下:
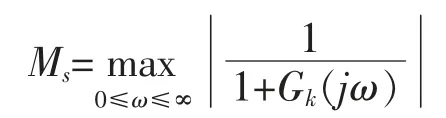
其中,Gk(s)表示系统开环传递函数;Ms一般取值为[1.2,2.0]。
由式(1)和式(2)得系统等效开环传递函数:
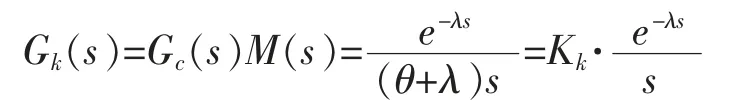
其中,Kk为开环增益,其形式表示如下:

文献[13]给出了开环增益Kk与Ms的关系式:

联立式(3)和式(4),由此可得内模控制器参数θ 值的整定方法:

以上可知,由于前期工作已经把高阶系统降阶为低阶系统,针对低阶系统基于内模控制原理设计的控制器此时只含有一个未知参数θ,再根据灵敏度指标Ms的取值范围确定控制器的唯一可调参数θ,既避免了参数选择的盲目性也提高工作效率。
5 仿真分析
例1 取高阶分数阶系统模型:
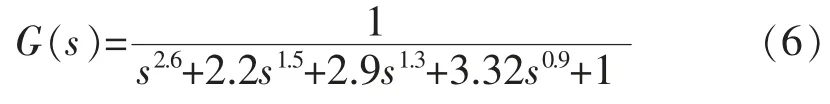
利用2 节的混合粒子群算法对其进行降阶处理,降阶后的模型如下:

为了进一步地验证本文降阶模型的优越性,分别取文献[12]和文献[13]降阶模型进行仿真对比。其中文献[12]的降阶模型为:

文献[13]的降阶模型为:

对模型(6)和降阶模型(7)、(8)、(9)进行阶跃响应仿真,如图4 所示。 从图4 中可知本文的降阶模型较好地逼近了原高阶系统模型,且其平方误差积分性能指标JISE的值为0.0058, 很好地证实了本文针对高阶系统所采用降阶方法的有效性和可行性。

图4 原模型与降阶模型阶跃响应曲线对比
根据灵敏度指标特性, 文中选取最大灵敏度Ms=1.2,由式(2)、式(5)、式(7)可得分数阶内模PID控制器为:

文献[12]设计的控制器为:
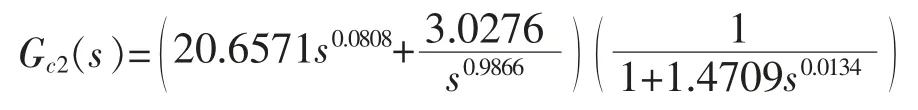
文献[13]设计的控制器为:
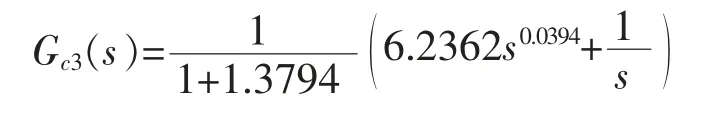
采用本文方法和文献[12]、文献[13]方法得系统的单位阶跃响应如图5 所示。 从图5 中可看出,本文设计的分数阶内模PID 控制器能使系统获得更好的跟踪特性,超调量较小,调节时间少,更好地体现了动态特性。 当t=20 s 时,设置+0.15 的阶跃输入扰动,即d(t)=+0.15(t-20)。 可看出本文方法能更好地抑制干扰。

图5 系统的单位阶跃响应曲线对比
在验证系统的鲁棒稳定性上, 改变系统的参数,即传递函数如下:
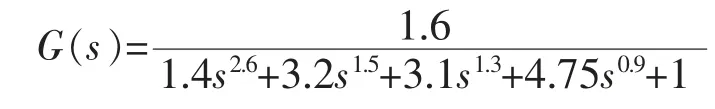
其单位阶跃响应曲线如图6 所示,从图6 中可看出,当参数发生变化时,本文设计的控制器具有更好的鲁棒性。
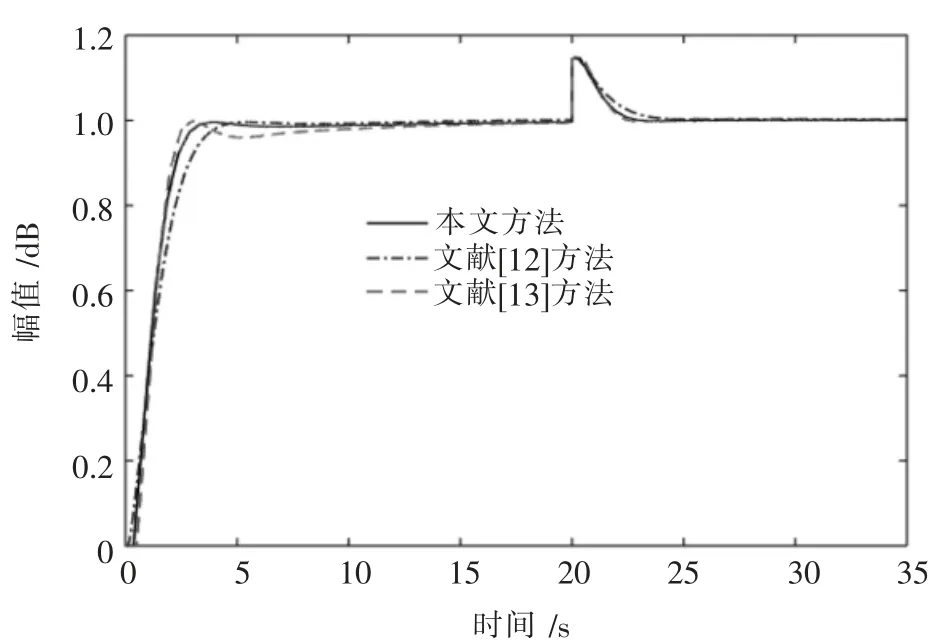
图6 系统参数摄动时单位阶跃响应曲线对比
例2 取高阶整数阶系统模型:

对其进行降阶处理,降阶后的模型如下:
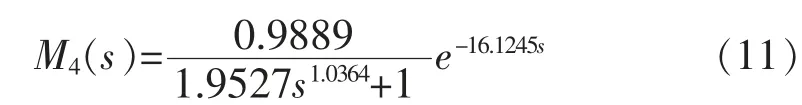
取文献[14]和文献[15]降阶模型进行仿真对比,其中文献[14]的降阶模型为:
文献[15]的降阶模型为:
对模型(10)和降阶模型(11)、(12)、(13)进行阶跃响应仿真,如图7 所示。 从图7 中可知本文的降阶模型较好地逼近了原高阶系统模型,且其平方误差积分性能指标JISE的值为0.0112 ,很好地证实了本文针对高阶系统所采用降阶方法的有效性和可行性。

图7 原模型与降阶模型阶跃响应曲线对比
根据灵敏度方法特性,选择最大灵敏度Ms=1.2,由式(2)、式(5)、式(11)可得分数阶内模PID 控制器为:
文献[14]设计的控制器为:
文献[15]设计的控制器为:

采用本文方法和文献[14]、文献[15]方法得系统的单位阶跃响应如图8 所示。 从图8 中可看出,本文设计的分数阶内模PID 控制器能使系统获得更好的跟踪特性,而且超调较小,调节时间少,更好地体现了动态特性。 当t=300 s 时,设置+0.3 的阶跃输入扰动,即d(t)=+0.3(t-300)。 可看出本文方法能更好地抑制干扰。

图8 系统的单位阶跃响应曲线对比
在验证系统的鲁棒稳定性上, 改变系统的参数,即传递函数如下:

其单位阶跃响应曲线如图9 所示,从图9 中可看出,当参数发生变化时,本文设计的控制器具有更好的鲁棒性。

图9 系统参数摄动时单位阶跃响应曲线对比
6 结 论
文中针对高阶次复杂控制系统在设计控制器中存在模型降阶、参数整定复杂等问题,提出了一种新型分数阶系统降阶模型,仿真结果显示新型降阶模型很好地逼近了原系统模型,证实了新型降阶模型的可行性。 在此基础上,根据内模控制思想设计了分数阶内模控制器,然后依据最大灵敏度指标完成对控制器的参数整定问题。 最后仿真实验证明,本文设计的分数阶内模控制器简单易行、参数整定方便,可使复杂高阶次控制系统具有良好的性能指标,同时也保证了较强的鲁棒稳定性,具有较好的优越性。
