中国男篮奥运会落选赛结果预测—基于篮球比赛制胜因素分析
2020-04-02王武天津理工大学中环信息学院
王武 天津理工大学中环信息学院
国际篮联篮球世界杯(FIBA Basketball World Cup)简称“篮球世界杯”,是国际篮球联合会(简称“国际篮联”)主办的世界最高水平的国际队级篮球赛事,每四年举办一次。2019年8月31日-9月15日,2019年国际篮联篮球世界杯的比赛分别在北京、广州、南京、上海、武汉、深圳、佛山、东莞八座城市进行。2019年篮球世界杯共有三十二支队伍参赛,总比赛场次60余场次,最终西班牙队取得了本项赛事的冠军[1]。
第32届奥林匹克运动会将于2021年7月23日至8月8日在日本东京举行。奥林匹克运动会中,男子篮球比赛项目也是国际篮球顶级赛事之一,目前已有8支球队获得了本项目的奥运会资格,剩下4个参赛名额将由2021年6月29日至7月4日举行的东京奥运会男篮资格赛(落选赛)决出。东京奥运会男篮资格赛(落选赛)共分4组,每组6支球队,小组第一名将获得奥运会参赛资格,中国队与希腊、捷克、加拿大、土耳其、乌拉圭在同一小组。
一、篮球比赛制胜因素分析
(一)数据选取以及标准化处理
本文选取中国男子篮球队在2019年篮球世界杯上的五场比赛数据,进行z-score标准化[2]处理后,可得到变准化数据,具体数据见表1。
(二)构造协方差矩阵
在统计学与概率论中,协方差矩阵的每个元素是各个向量元素之间的协方差,是从标量随机变量到高维度随机向量的自然推广[3]。
令为n维随机变量, 为第i个向量与第j个向量的协方差[8]。则其相应的协方差矩阵为:

由上述方法,容易计算表二数据的协方差矩阵为:

(三)主成分分析
通过MATLAB计算得到协方差矩阵的11个特征值,从大到小排列有:(见表2)

表1 中国男子篮球队在2019年篮球世界杯上的五场标准化后的数据

表2 协方差矩阵的特征值
前四个特征值得和为11,11个特征值的和为11.25,则这四个特征值占总特征值的99%,则选取前四个特征值所对应的特征向量为新的指标因素,而且这四个指标能够很全面的反应原数据。
记这四个新的指标因素为第一、第二、第三、第四主成分,记号分别为F1、F2、F3、F4,由前四个特征值所对应的特征向量得4个主成分。
四个主成分的权重分别为:35%、30%、22%、13%,根据个主成分权重,构造新的综合指标z为:

z-值越大,说明中国男子篮球队在这场比赛表现越好,z-值越小,说明中国男子篮球队在这场比赛表现越差。
二、东京奥运会男篮资格赛(落选赛)比赛结果预测
层次分析法,简称AHP,是指将与决策总是有关的元素分解成目标、准则、方案等层次,在此基础之上进行定性和定量分析的决策方法。该方法是美国运筹学家匹茨堡大学教授萨蒂于20世纪70年代初,在为美国国防部研究"根据各个工业部门对国家福利的贡献大小而进行电力分配"课题时,应用网络系统理论和多目标综合评价方法,提出的一种层次权重决策分析方法[4]。
(一)数据选取以及标准化处理
选取了中国队、希腊、捷克、加拿大、土耳其在2019年篮球世界杯中的数据以及乌拉圭队在2019年篮球世界杯预选赛中的数据。采用z-score标准化处理方法对数据进行标准化处理,得到表3的数据。
(二)建立层次结构模型
建立层次结构模型,目标层为获得“奥运会参赛资格”,因素层为“第一主成分”“第二主成分”“第三主成分”“第四主成分”,方案层为中国队、捷克队、土耳其队、希腊队、加拿大队、乌拉圭队。具体层次结构模型如图1所示。
(三)构造判断(成对比较)矩阵
通过第一部分,我们找出了影响比赛胜负的4个综合因素,即第一主成分、第二主成分、第三主成分、第四主成分。表2确定的数据矩阵与11个影响因素在各个主成分中的权重矩阵乘机,可以得到各支球队在相应4个主成分中的权重,具体权重见表4。
在确定各层次各因素之间的权重时,如果只是定性的结果,则常常不容易被别人接受,因而本文采用一致矩阵法,即不把所有因素放在一起比较,而是两两相互比较,对此时采用相对尺度,以尽可能减少性质不同的诸因素相互比较的困难,以提高准确度。如对某一准则,对其下的各方案进行两两对比,并按其重要性程度评定等级。aij为要素i与要素j重要性比较结果。按两两比较结果构成的矩阵称作判断矩阵。判断矩阵具有如下性质:

表3 中国队、希腊、捷克、加拿大、土耳其在2019年篮球世界杯中的数据以及乌拉圭队在2019年篮球世界杯预选赛中的标准化后的数据
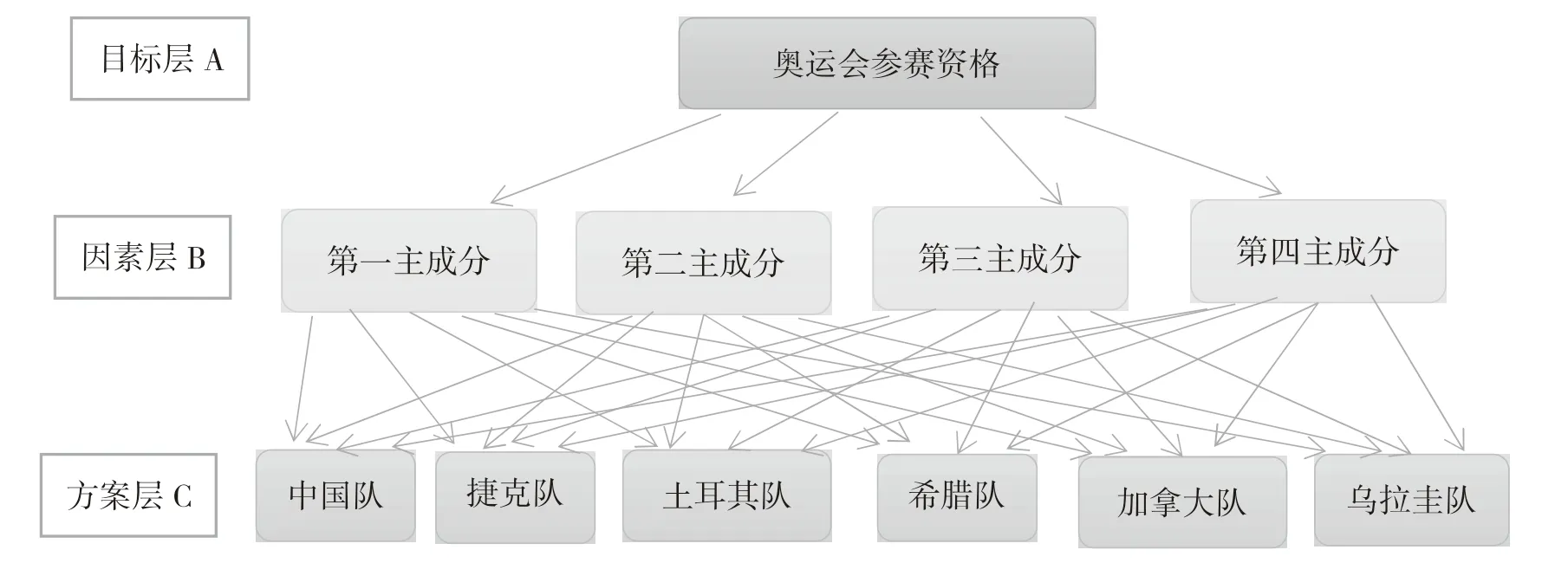
图1 层次结构模型
方案层对第一个因素即第一主成分的比较矩阵的构造方法为:(1)将表3.3中第一主成分列加除以-0.27,若结果为正,则令 ,若结果为负,则令 ,可以得到比较矩阵的第一行,同理可得到比较矩阵第二至六行,即可得到方案层对第一、第二、第三、第四主成分的比较矩阵。
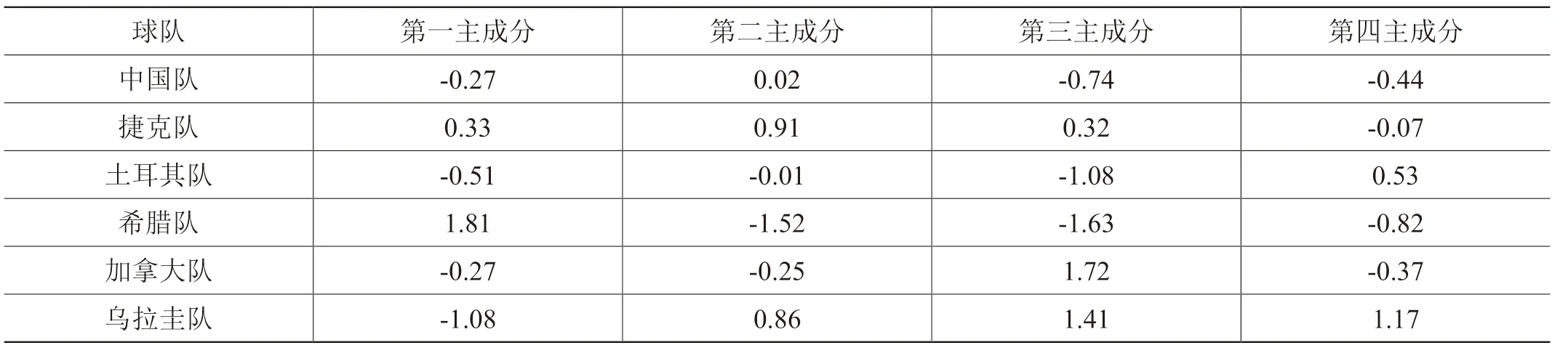
表4 各支球队在相应4个主成分中的权重
在本文第一部分可知,第一至四主成分对目标层的权重分别为35%,30%,22%,13%,令 ,则得到准则层对目标层的比较矩阵。
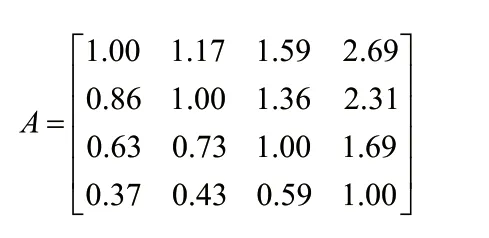
通过对比较矩阵的一致性检验,上述比较矩阵皆满足一致性,可以用于层次分析法选择最终的方案。
通常的层次分析法一般采用主观判断的方式确定比较矩阵,本文采用各球队的相关数据的差别构造的比较矩阵,这就避免了人为因素的影响,同时可以将各因素量化,提高准确性。
(四)层次单排序与层次总排序
取相应比较矩阵的最大特征值所对应的特征向量为下一层因素对本因素的权重,可得方案层对准则层、准则层对目标层的层次单排序得到如下成分单排序。
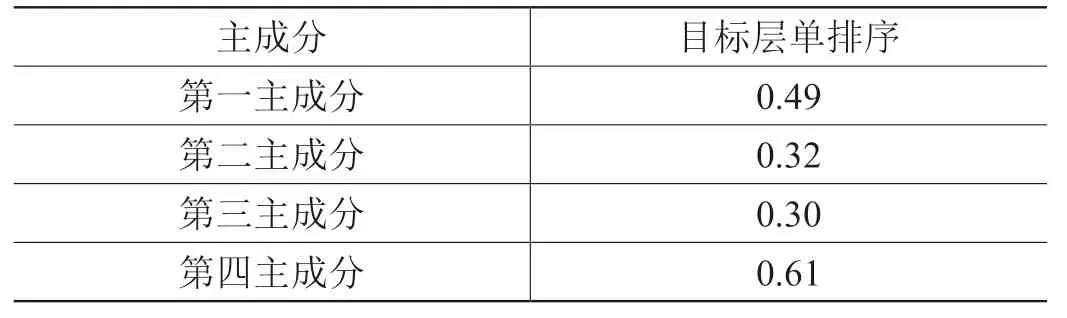
?
记方案层对目标层的层次总排序为方案层对因素层的层次单排序矩阵 ,因素层对目标层的层次单排序为 ,则方案层对目标层的层次总排序为 ,通过计算得到层次总排序。

?
由层次总排序可知,捷克队的权重排序第一,这说明本小组捷克队会获得东京奥运会男篮资格赛(落选赛)本小组的第一名,从而获得奥运会参赛资格。捷克队进攻与防守均衡,注重传切结合,在2019年中国篮球世界杯中取得了第六名的成绩,这也在侧面说明捷克队出线的概率最大,我们的预测结果比较合理。
(五)结果分析
本文采用层次分析法,给出了东京奥运会男篮资格赛(落选赛)中国队等六支球队所在小组的权重排序,捷克队排序最靠前,取得小组第一的可能性最大。其次,加拿大队排序在第二位,也有较大可能性取得小组第一。其他三支球队权重值与捷克队、加拿大队相差较大,取得小组第一的可能性较低。
三、结语
综上所述,本文首先利用主成分分析法将影响篮球比赛胜负的11个因素整合为4个综合影响因素,并且这4个综合影响因素在很大程度上反映了原来11各因素所代表的信息。同时,针对各因素在4个综合因素中的权重,给出了中国男子篮球队一些建议。其次利用层次分析法,预测了东京奥运会男篮资格赛(落选赛)中国男子篮球队所在的小组的出线情况,通过预测,捷克男子篮球队会获得东京奥运会的参赛资格。
中国男子篮球队一直是国际篮球赛场上的传统强队,近年来受人才培养、篮球协会改革、球员伤病等因素影响,成绩不理想。随着体制改革的进行,中国男子篮球队在篮球人才培养、竞技环境、对外交流等方面会取得长足的进步,相信在不久的将来,中国男子篮球队会继续出现在国际大赛的舞台。
