基于MRAS的异步电机无速度传感器应用研究

包广清，祁武刚

(兰州理工大学 电气工程与信息工程学院，兰州 730050)

0 引 言

在自动化装配领域中，工业机械臂是最常见的形式。异步电机无速度传感器矢量控制技术由于成本低、可靠性高的特点,被广泛应用于机器人的关节驱动控制系统中。目前，已经有多种方法实现了对异步电机的速度辨识，如扩展Kalman[1-2]、线性矩阵不等法[3]、滑模观测器[4]、全阶观测器[5]和模型参考自适应法[6]等。

模型参考自适应(以下简称MRAS)由于算法简单、稳态精度较高已被广泛应用于电机的控制，但仍存在一定的缺陷。

基于转子磁链模型的MRAS观测器，在低速时检测精度差，且存在积分误差和误差积累的问题[7]；文献[8]将无功功率与MRAS相结合，收敛速度较快，鲁棒性也有所提高，但未考虑电机参数变化时的转速辨识问题；文献[9]利用反电动势的MRAS转速观测器，成功地避开了纯积分的问题，但是此方法在低速时估计值误差值较大；文献[10]将滑模控制策略作为MRAS结构中的自适应机制，但电压参考模型中依然存在纯积分的问题；文献[11]采用一种可以同时进行转速和定子电阻辨识的双参数的MRAS模型，此方法对电机的定子电阻辨识度较高，却增加了系统的复杂性；文献[13]提出以模糊逻辑作为MRAS结构中的PI自适应率，此方法改善了传统PI参数不能在线更新的问题，却忽略了电压参考模型中的积分问题。

本文在基于转子磁链模型的MRAS速度观测器的基础上，采用一阶惯性环节代替电压模型中的纯积分环节，以消除积分直流偏置的问题，同时设计了一种自适应线性(以下简称ADALINE)神经元PID控制器，ADALINE可以根据电机磁链、转速的变化情况对自身的参数进行在线权值修正，该控制器改善了传统的PI控制器不能根据电机的实际情况进行在线参数修正的问题，提高了速度观测的精度。仿真结果验证了该算法的可行性。

1 异步电机数学模型

三相异步电机在两相静止坐标系α，β下的电压方程：

(1)

式中：usα，usβ为定子绕组电压在α，β轴分量；urα，urβ为转子绕组电压在α，β轴分量；isα，isβ为定子绕组电流在α，β轴分量；irα，irβ为转子绕组电流在α，β轴分量；ψsα，ψsβ为定子绕组磁链在α，β轴分量；ψrα，ψrβ为转子绕组磁链在α，β轴分量；Rs,Rr为定、转子单相绕组电阻；ω为转子角速度。

磁链方程：

(2)

式中：Ls,Lr为α,β坐标系上定、转子绕组自感；Lm为α,β坐标系上同轴定、转子绕组间的互感。

转矩方程：

Te=pLm(isβirβ-isαirβ)

(3)

式中：Te为电磁转矩；p为异步电动机的极对数。

运动方程：

(4)

式中：J为机组的转动惯量；TL为包括摩擦阻转矩的负载转矩。

2 无速度传感器的速度观测模型

2.1 MRAS速度观测器的原理

转子磁链观测器有两种不同的模型：电压模型和电流模型。

电压模型：

(5)

电流模型：

(6)

由式(5)和式(6)可知，ω是待辨识的参数。如图1所示的速度辨识系统中，可调模型和参考模型分别为转子磁链的电流模型和电压模型。

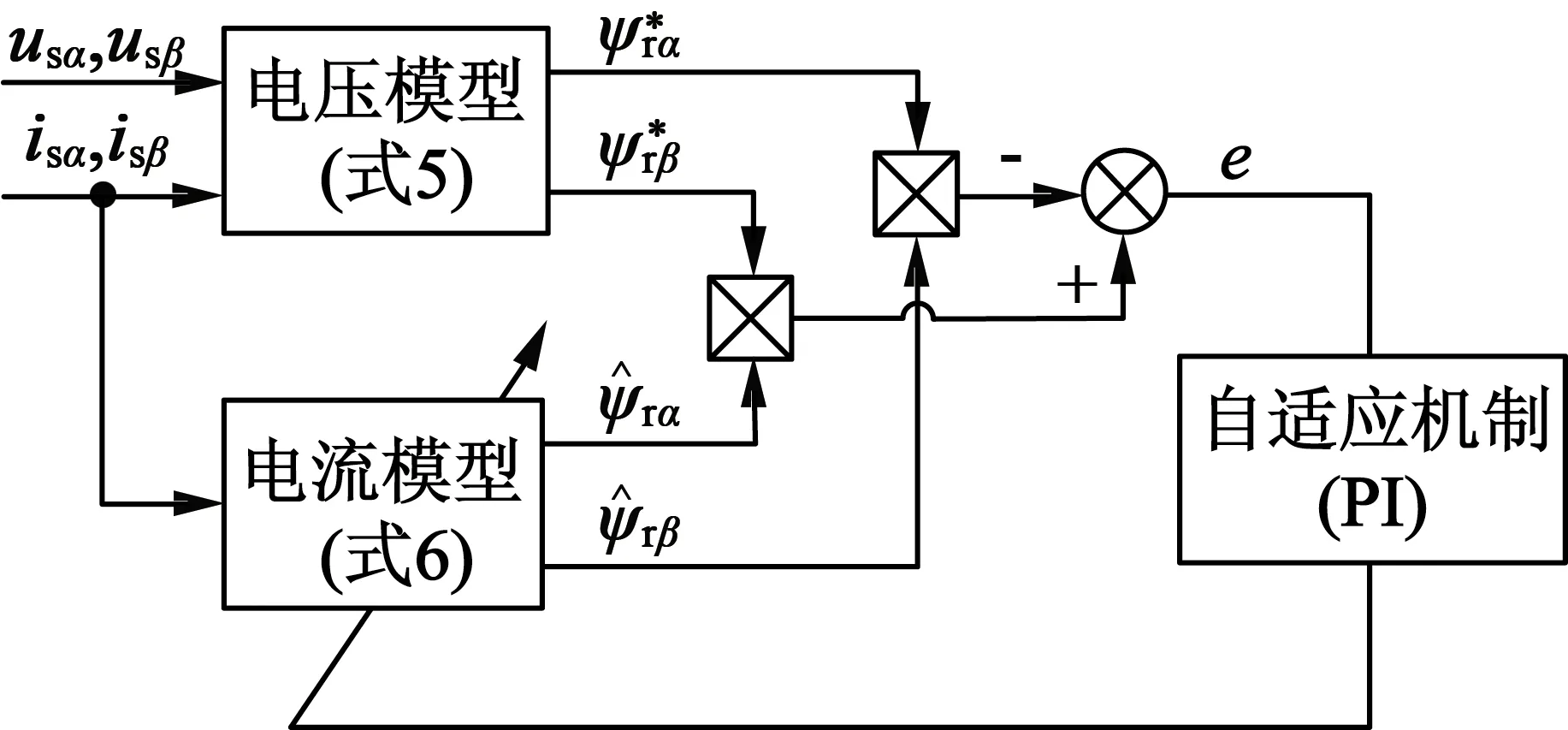
图1 MRAS速度辨识框图

根据Popov超稳性定律，该MRAS系统是渐进稳定的。在图1中取广义误差e作为MRAS自适应律的输入值,定义广义误差e：

(7)

以PI为MRAS自适应率，计算电动机转速ωr：

(8)

式中：KP为比例系数；KI为积分系数。

2.2 改进的MRAS转速估算方法

转子的反电动势：

(9)

转子磁链估计的动态方程：

(10)

图2 改进后的电压模型原理图

2.3 基于ADALINE的并联双模型速度辨识

传统的基于转子磁链的MRAS转速辨识方法中，PI调节器不能根据电机磁链、转速的变化进行在线修正，因此其误差较大。本文将ADALINE作为MRAS的自适应机构，其权重参数在线修正，所以使得速度观测更加准确。

由式(7)，采用PI调节器对磁链的广义误差进行处理，但PI参数的选取受制于异步电机的数学模型，事先选取适合的PI参数存在一定的困难。而ADALINE可根据外界的输入和期望响应，其权值进行动态的调整，因此采用ADALINE代替传统MRAS中的PI自适应率。ADALINE模型如图3所示。

图3 ADALINE结构模型

图3中：x1(k),x2(k)和x3(k)为输入信号；ω1(k),ω2(k),ω3(k)输入信号的权重。根据转子的广义误差e，定义状态变量：

(11)

(12)

为了保证系统的收敛性，采用最小均方误差算法(以下简称LMS)来修正ADALINE的加权系数。定义目标函数：

(13)

LMS算法是一种特殊的梯度估计算法，其权重系数采用反梯度向量进行反复迭代更新。根据梯度法，其权值系数的修正公式如下:

(14)

将式(12)和式(13)代入求偏导，可得：

(15)

(16)

结合式(11)、式(14)、式(15)、式(16)，得到速度观测器中权值自学习的差分表达式：

(17)

根据每次转子磁链估计误差计算此时的状态变量，由式(17)进行权值更新，由式(11)得到电机的转速估计。

3 仿真与结果分析

改进后的MRAS速度观测器的控制系统如图4所示，并在MATLAB/Simulink环境下对此控制模型进行仿真分析。

图4 基于改进的MRAS速度观测器控制框图

电机的仿真参数如表1所示。

表1 电机的参数

电机给定转速为1 000 r/min,空载起动，0.08 s时转速上升至2 200 r/min，仿真结果如图5所示。图5(a)为电机定子间的线电压;图5(b)为转速辨识与电机实测转速的仿真图，从图5(b)中可知，辨识转速的波动较小，较好地跟随电机的实际转速；图5(c)为转速的误差图，由图5(c)可知，电机的在稳态时误差很小，响应速度快；图5(d)为电机的输出转矩；图5(e)为定子电流；图5(f)为转子磁链运行轨迹图。

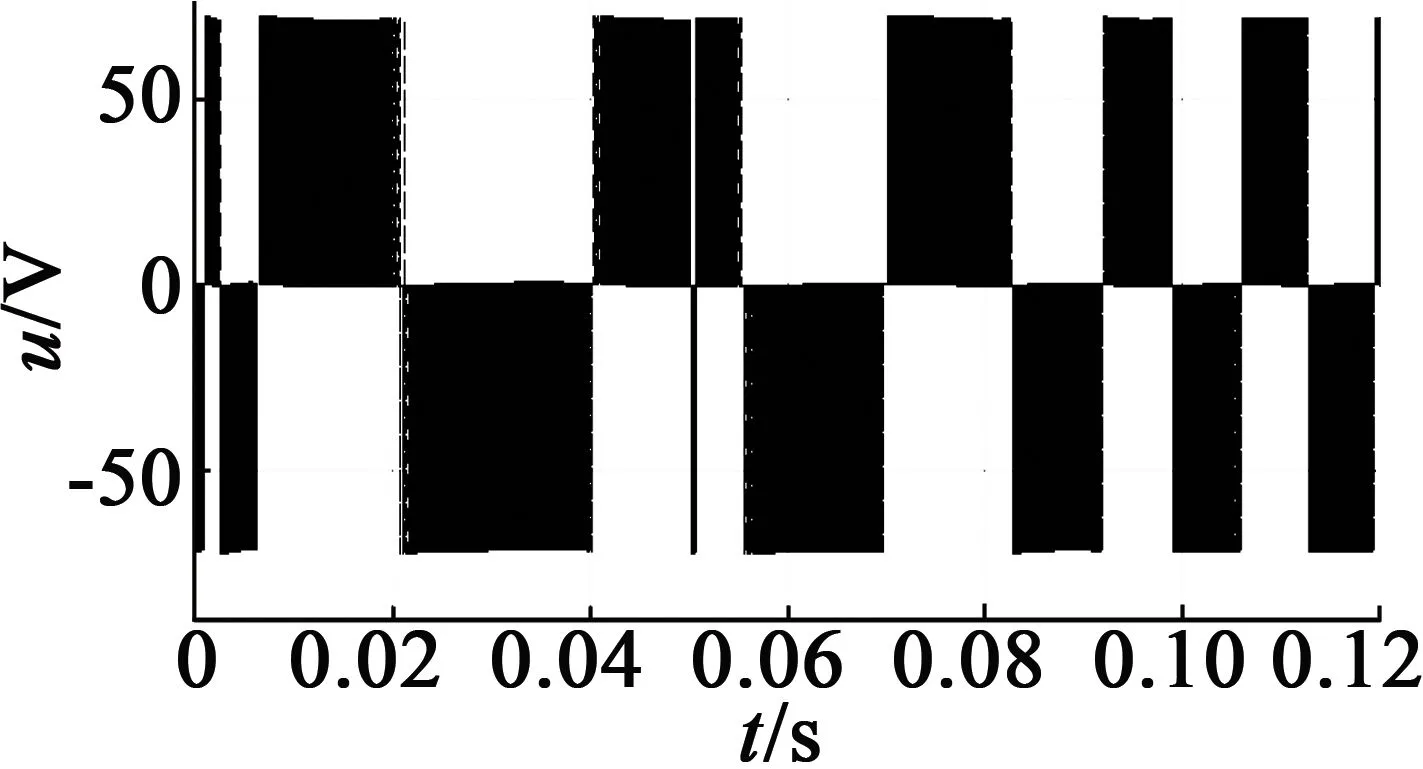
(a) 定子线电压

(b) 转速响应

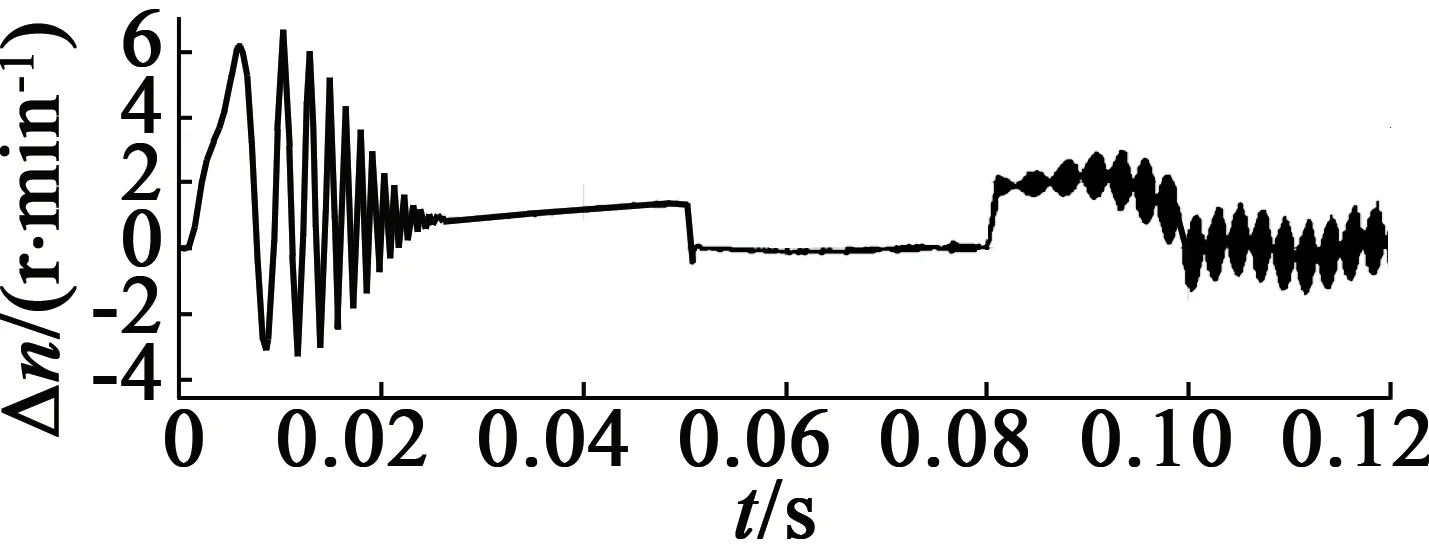
(c) 转速误差

(d) 电磁转矩

(e) 定子电流

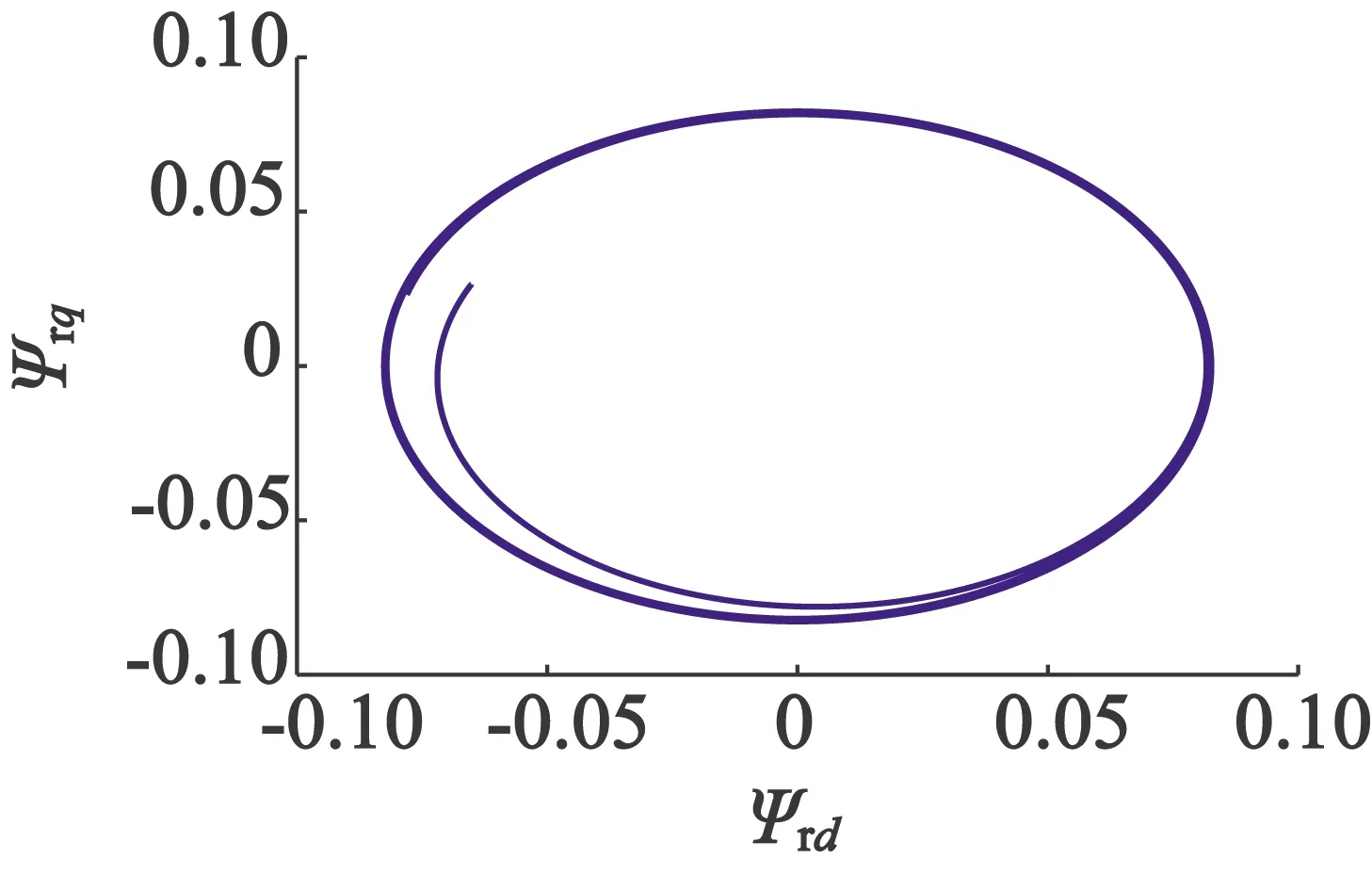
(f) 转子磁链

图6给定电机转速为1 000 r/min,在0.06 s突加负载20 N·m，0.08 s时负载减至10 N·m的仿真结果。从图6中可知,突加负载后转速略有下降，但立即恢复。

(a) 定子线电压

(b) 转速响应

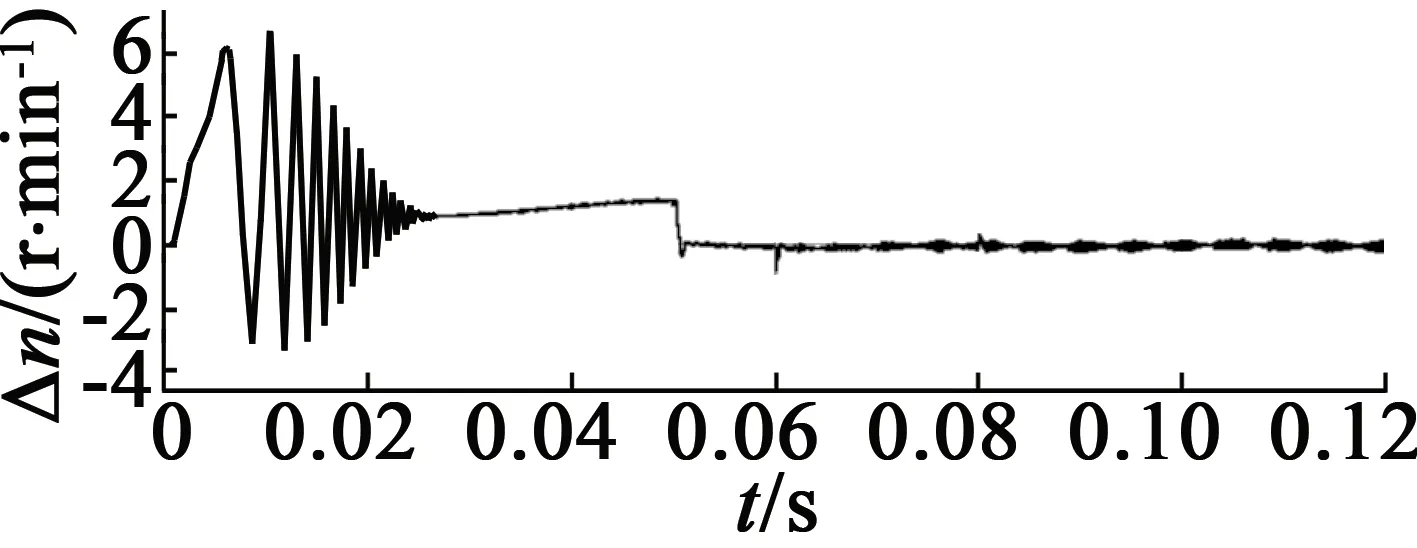
(c) 转速误差

(d) 电磁转矩

(e) 定子电流

4 结 语

本文以转子磁链的电压模型和电流模型作为MRAS速度观测器的参考模型和可调模型，采用了一阶惯性滤波环节消除电压模型中的纯积分问题，利用ADALINE在线权值修正的特点，设计了一种自适应神经元PID控制器，并将此控制器作为MRAS结构中的自适应机制。最后在转速为1 000 r/min和2 200 r/min的情况下进行了仿真验证，其结果表明，电机速度辨识精度较高，动态性能也得到了改善。