谐波影响下的三相感应电机效率研究
2020-03-25叶伟玲汤铭华陈子辉冯君璞严柏平
杨 玺,叶伟玲,汤铭华,陈子辉,冯君璞,严柏平,殷 豪
(1.广东电网有限责任公司江门供电局,江门 529000 ;2.广东工业大学,广州 510006)
0 引 言
三相感应电机由于具有轻量化、高转速、电机效率较高等优点,被广泛应用于制造生产业。据统计,现在我国每年发电量中60%用于电机,而其中90%是感应电机消耗。
三相感应电机控制电路中包含非线性器件,使电能质量下降。谐波电压形成电流谐波、磁场谐波。电流谐波将生成绕组损耗及铁心损耗,令感应电机效率降低;磁场谐波干扰电机起动性能,生成脉动转矩,导致转速波动。分析谐波对三相感应电机运行效率的影响,对于在电能质量较差地区的三相感应电机的选型有重要意义[1-3]。
目前,国内外学者对三相感应电机在谐波影响下的运行特性已做了一些研究。文献[4]通过仿真得出电机气隙磁密分布,并进行谐波分析,对谐波影响下电机电磁振动情况进行了分析。文献[5]使用时步有限元分析异步电机在供电电源包含谐波的情况下的气隙磁密、损耗情况,对电机谐波变化下的损耗变化进行分析。文献[6]通过磁路法、数值法、测试方法对感应电机进行性能计算。文献[7]分析三相感应电机的能量等效模型,使用MATLAB编制谐波污染下三相异步电机损耗计算软件,再通过有源电力滤波器对谐波进行谐波的抑制与消除。文献[8]使用时步有限元仿真揭示定转子铁损密度分布规律,研究电机结构参数对电机损耗的影响。文献[9-12]通过不同方式分析感应电机的结构参数如槽数、极对数、气隙宽度对电机的性能、效率的影响,而在这之中气隙宽度对感应电机能效的影响最为突出。
上述文献都对三相感应电机在谐波下的磁密、损耗进行分析,但一般仅对特定型号电机使用。却少有探究谐波及结构参数、输出转矩与三相感应电机效率的普遍适用规律。规律对于在电能质量较差地区三相感应电机的型号选取及使用有较大意义。
本文针对三相感应电机在含谐波的输入源时的电机转矩及功率变化进行了分析,拟合出以相同输出容量下谐波种类i、谐波含量UHCi、转矩相对变化值ΔT、气隙宽度δ为输入量,电机效率η为输出量的效率计算公式。
1 谐波分析
文献[13]说明三相对称绕组中3次谐波的合成磁动势f3为0。在对称的三相感应电机中,3的倍数次谐波磁动势f3k也有相同性质。
通过上述分析,干扰三相感应电机的谐波主要为5,7,11次谐波。由此确定的输入电压:
UHC7sin(14πft)+UHC11sin(22πft)]
式中:UHC0,UHC5,UHC7,UHC11分别为基波含量,以及5,7,11次的谐波含量。
谐波含量UHC的计算公式:
式中:Uhn为n次谐波;Urms为有效值。
同时,三相感应电机的效率影响成分中,结构参数占一个重要部分。除气隙宽度外的其他结构参数对三相感应电机的效率影响较小,由于气隙宽度改变直接导致功率因数的改变,所以我们选取气隙宽度为输入量。
三相感应电机转矩和效率公式如下:
由此可知,三相感应电机效率与转矩相对变化值ΔT相关。
2 有限元仿真
三相感应电机Y160M-4参数如表1所示。
Maxwell中的2D电磁结构有限元模型如图1所示。
对于中小型异步电机而言,气隙宽度一般为0.5~1.5 mm。为使三相感应电机效率计算公式具有普遍性,分别设计气隙宽度为0.5 mm,1 mm,1.5 mm且具有相同输出容量的三相感应电机。
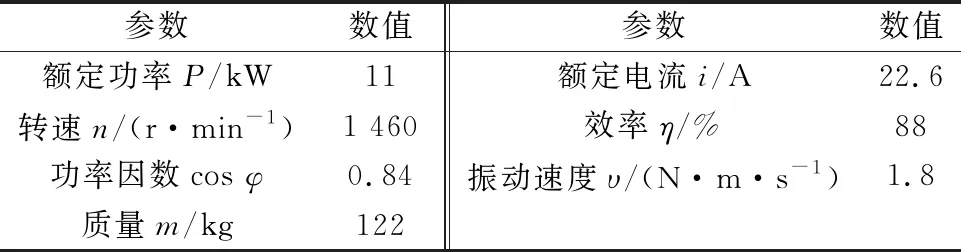
表1 Y160M-4参数
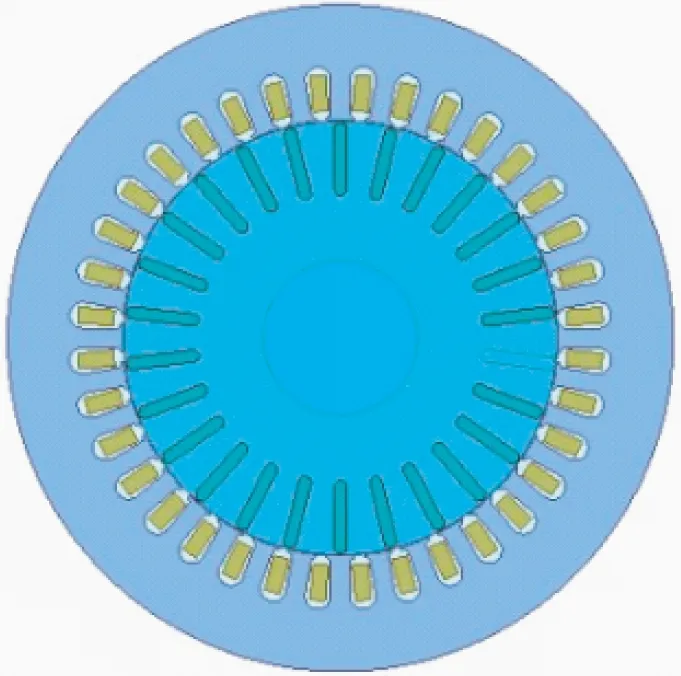
图1 有限元结构模型
ANSYS中设置输入谐波电源,进行电机仿真。
(1)单一谐波下,输入谐波含量为2%~10%,分析单一谐波下的电机输出转矩、功率的影响,并比较5,7,11次谐波对三相感应电机影响程度。
(2)输入多谐波,分析多谐波与单一谐波对三相感应电机输出转矩、功率影响程度的差异。
2.1 单一谐波下,相同气隙宽度、不同谐波含量下转矩曲线
图2是气隙宽度为0.5 mm,5次谐波含量为2%、10%的转矩曲线。由图2可知,在相同气隙宽度下,三相感应电机输出转矩与5次谐波含量成反比,且振荡程度与5次谐波含量成正比。

图2 5次谐波含量为2%、10%转矩
2.2 单一谐波下,相同谐波含量、不同气隙宽度下转矩曲线
图3是气隙宽度为0.5 mm、1 mm、1.5 mm,5次谐波含量为2%的转矩曲线。在相同谐波含量下,三相感应电机的输出转矩与气隙宽度成反比,而输出转矩的振荡程度与气隙宽度成反比。

图3 不同气隙宽度下转矩
2.3 单一谐波下,相同气隙宽度、不同谐波含量下功率曲线
图4是气隙宽度为0.5 mm,5次谐波含量为2%、10%的电功率曲线。在相同气隙宽度下,三相感应电机电功率与5次谐波含量成反比,同时电功率振荡程度与5次谐波含量成正比。

图4 5次谐波含量为2%、10%电功率
图5是气隙宽度为0.5 mm,5次谐波含量为2%、10%的机械功率曲线。在相同气隙宽度下,三相感应电机机械功率与5次谐波含量成反比,同时机械功率振荡程度与5次谐波含量成正比。
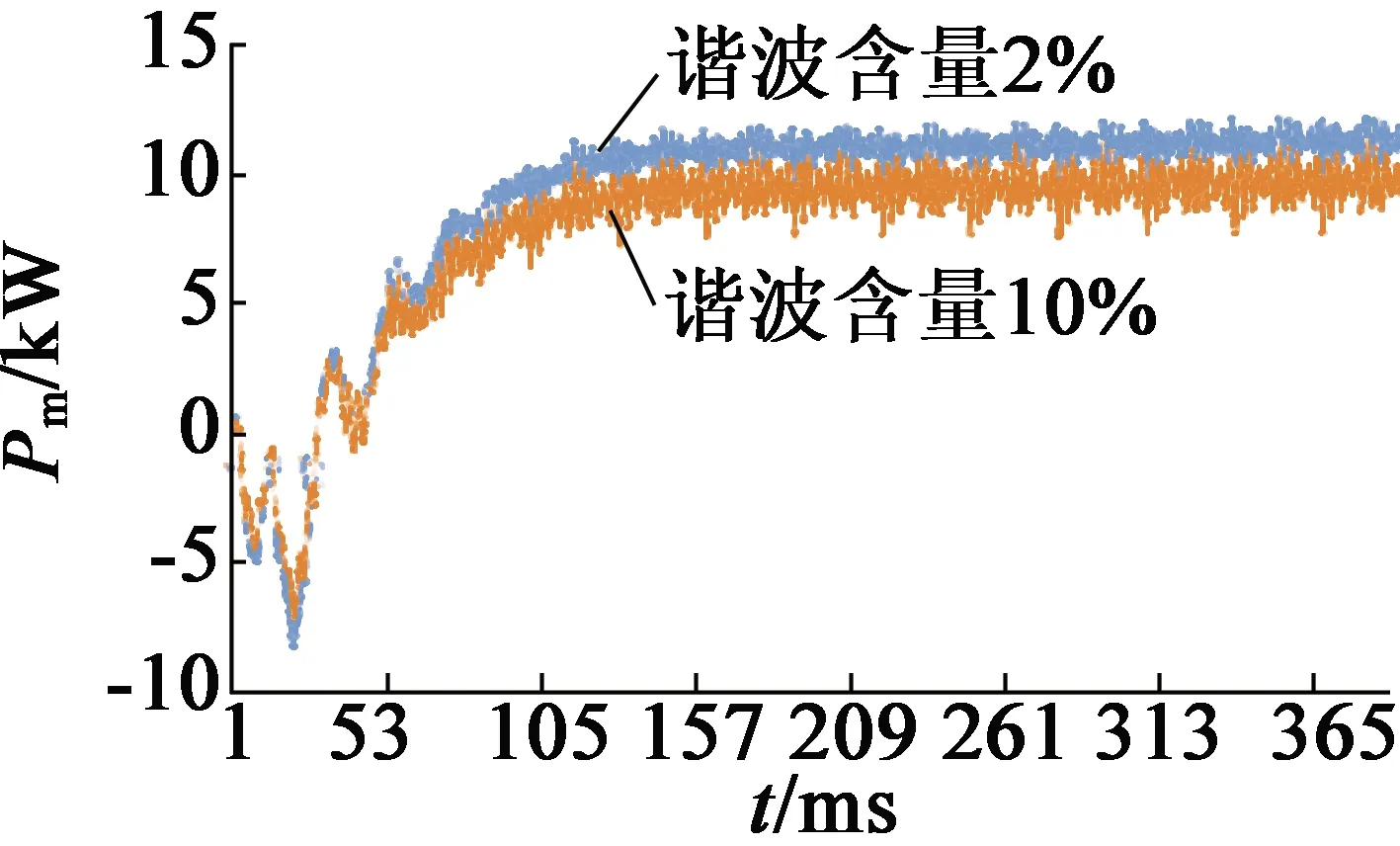
图5 5次谐波含量为2%、10%机械功率
2.4 多谐波,不同谐波含量组合下转矩相对值、效率曲线
图6、图7是气隙宽度为0.5 mm、1 mm、1.5 mm下三相感应电机效率、转矩相对值与多谐波组合的对比图。多谐波组合5次、7次、11次谐波含量分别为2%+1%+2%、3%+2%+1%、3%+3%+1%、5%+3%+1%,分别对应横坐标1、2、3、4。效率与多谐波种类、含量成反比,转矩相对值与多谐波种类、含量成正比。同时可知,随气隙宽度变大,电机效率下降,转矩相对值下降。
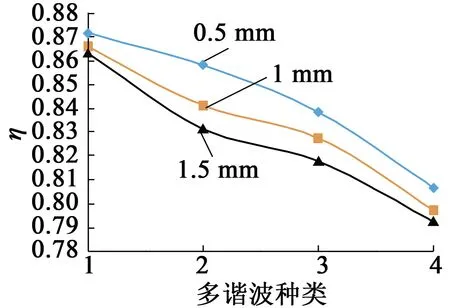
图6 多谐波含量与电机效率

图7 多谐波含量与转矩相对值
2.5 多谐波下,不同气隙宽度下转矩相对值与效率曲线
图8是气隙宽度为0.5 mm、1 mm、1.5 mm下三相感应电机效率、转矩相对值对比图。由图8可知,电机效率与转矩相对值成反比。同时,随着气隙宽度变大,电机效率下降,转矩相对值下降。

图8 多谐波下转矩相对值与气隙宽度、电机效率
3 数据处理
根据所得的三相感应电机转矩、功率特性曲线,在电机运行稳定后取点获取数据,对数据进行处理。
转矩平均值:

转矩峰峰值:
Tff=Tmax-Tmin
式中:Tmax,Tmin为最大转矩和最小转矩。
转矩变化相对值:

电功率平均值:
式中:P1e,P2e,P3e,…,Pne为电机达到稳态后电功率的瞬时值。
机械功率平均值:
式中:P1m,P2m,P3m,…,Pnm为电机达到稳态后机械功率的瞬时值。
电机效率:
式中:Pm为电机的机械功率;Pe为电机的输入功率。
得出处理后的数据,进行MATLAB多元线性回归数据拟合,步骤如下:
(1)生成自变量和因变量的散点图,判断能否进行多元线性回归。
(2)输入自变量和因变量。
(3)输入命令:[b,bint,r,rint,s]=regress(y,X,alpha)rcoplot(r,rint),可得回归模型的系数、异常点的情况。
(4)检验回归模型:
回归模型残差的正态性检测:单样本正态分布Jarque-Bera检测,单样本均值t检测。
回归模型残差的异方差检测:戈得菲尔德——匡特检测。
~F[(n-c)/2-k-1,(n-c)/2-k-1]
式中:n是样本容量;k是自变量数量。
残差的自相关性检测。DW检验:
式中:et是残差序列,后查表对比。
du DW>dl,一阶的正相关性; DW>4-dl,一阶的负相关性; dl 其中,du为残差自相关检测的上临界值,dl为下临界值,通过样本容量n和自变量k查表所得。 图9 数据散点图 图10 异常点检测图 通过MATLAB对转矩数据曲线进行拟合,可得谐波下电机效率η与三相感应电机的气隙宽度δ、电机转矩变化相对值ΔT、输入谐波含量UHCi(5、7、11次谐波)间拟合公式(适用于单一谐波及多谐波下): η=β0+β1UHC5+β2UHC7+β3UHC11+β4ΔT+β5δ 式中:β0~β5为拟合系数,β0=0.889 3,β1=-0.349 2,β2=-0.204 0,β3=-0.126 8,β4=-0.005 8,β5=-0.007 5。 拟合系数的置信区间如表2所示。 表2 参数置信区间 本文通过ANSYS有限元仿真建立多个不同结构参数的三相感应电动机。首先,分析得出电机外输出特性与谐波间的变化关系。然后,通过数据拟合公式,以三相感应电机的效率η为因变量,以谐波种类i、谐波含量UHCi、气隙宽度δ、转矩变化相对值ΔT为自变量。同时公式输入变量中包含多种电机结构参数、输出特性,对不同型号三相感应电动机具有普遍适用性。本文的研究对于实际电机选型有一定指导意义。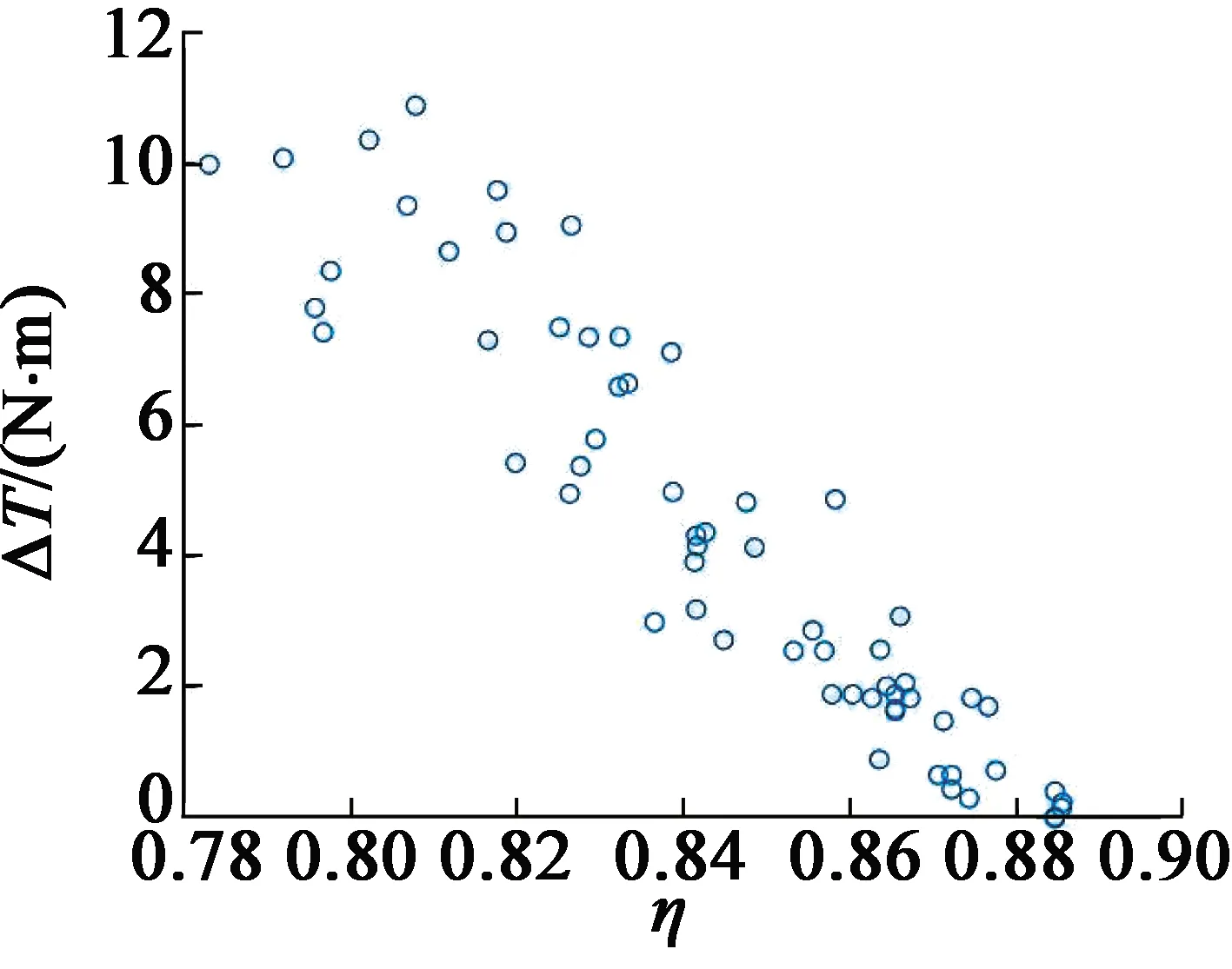
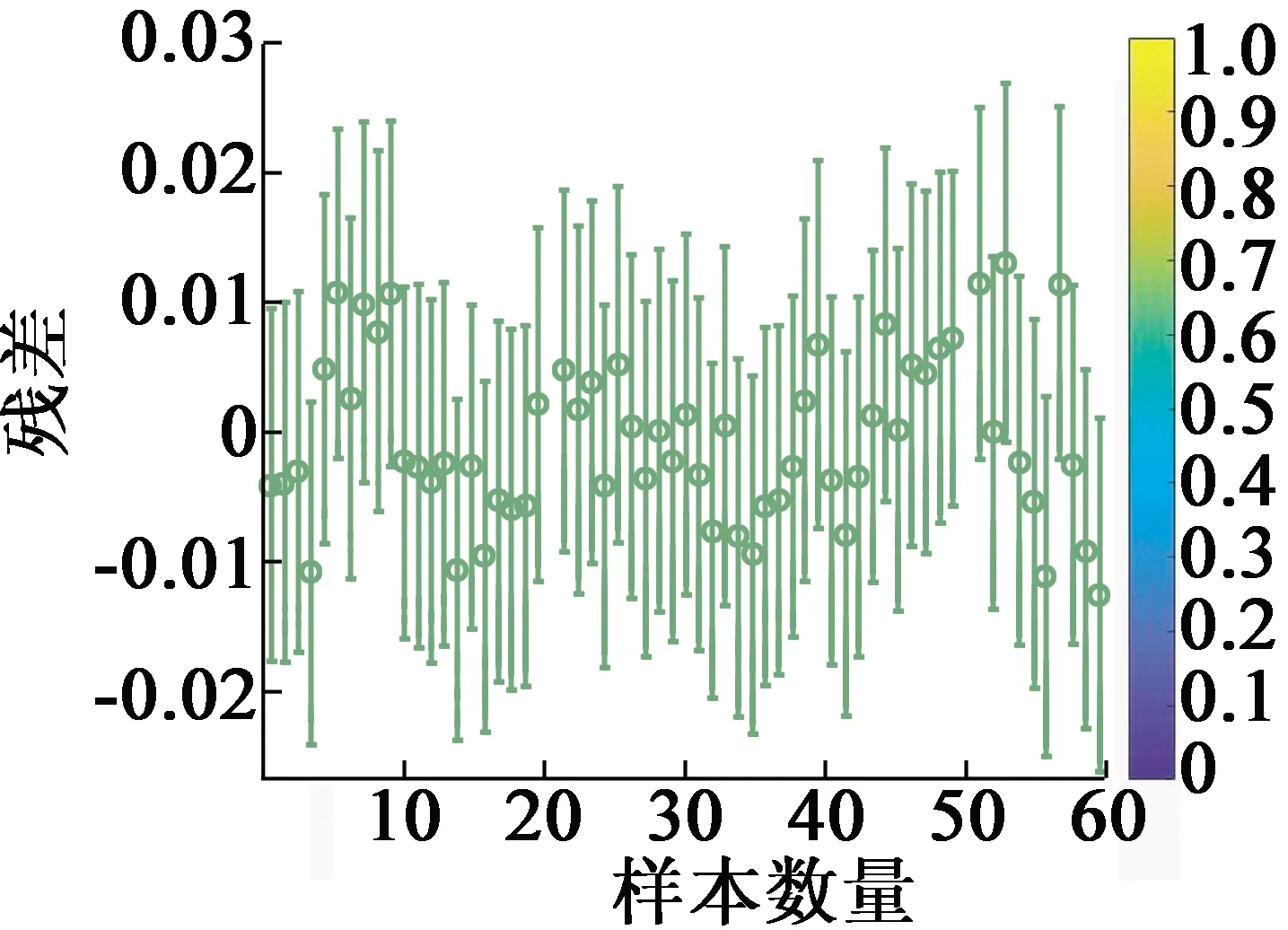

4 结 语
