一种感应电机转子断条故障建模方法

李楷然，刘永强，吴立泉，梁兆文

(华南理工大学 电力学院，广州 510000)

0 引 言

感应电机已被广泛应用于工业领域，持续不断地为社会创造价值。对于处在生产线上持续运作的电机，发生故障导致停机对企业造成的经济损失是巨大的。对于这类企业，凸显了及早发现电机故障早期特征的重要性。在感应电机的各类故障中，轴承故障出现概率为41%，定子故障出现概率为37%，转子故障出现概率为10%，气隙偏心及其它故障出现概率为12%，因此，感应电机转子故障诊断对社会经济发展具有重要意义。

感应电机故障诊断常用的方法有定子电流特征分析法[1-3]、瞬时功率分析法[4-5]、振动诊断方法[6-7]、PARK空间矢量法[8-9]、气隙转矩分析法[10]、参数辨识的方法[11-12]和数据融合的方法[13-15]，其中定子电流特征分析法是比较成熟和常用的方法，又可细分为快速傅里叶分析方法、小波分析方法、多窗谱分析方法和Hilbert模量频谱分析方法等。随着机器学习的发展和应用，当前越来越多地将各类方法与神经网络相结合[16-19]来诊断电机故障。对于感应电机转子早期断条故障诊断，各方法均没有给出一个较好的解决方案，导致转子早期断条故障特征不能被准确获取，影响了感应电机转子早期断条故障的判别。

运用参数辨识方法进行感应电机故障诊断时，关键是准确建立感应电机故障模型。文献[20]针对鼠笼式感应电机提出了多回路模型，能够准确地描述感应电机断条情况，但应用于感应电机转子断条故障诊断时，方程数较多，且需要针对断条位置建立不同模型，这在电机断条位置未知的情况下计算量是非常大的。本文基于鼠笼式感应电机多回路模型，提出了一种感应电机转子断条建模方法。该方法相较于多回路模型，方程数大为减少，结合参数辨识和滑窗技术能够将感应电机转子断条的特征信号提取出来。仿真验证了方法的有效性。

1 感应电机多回路模型方程

感应电机多回路模型是把电机转子按实际回路来列写方程[20]，分为电压方程和磁链方程：

电压方程：

[iaibici1i2…inie]T+

p[φaφbφcφ1φ2…φnφe]T

(1)

磁链方程：

[iaibici1i2…inie]T

(2)

由文献[21]可得电感系数Mxy的一般化计算公式：

(3)

式中：iy为电流；φxy为磁链；Λg为气隙磁导；Nx和Ny分别为x相和y相绕组的串联匝数；p为电机极对数；αxy为x相绕组轴线和y相绕组轴线之间的电角度。有：

式中：μ0为气隙磁导率；τ为极距；l为铁心有效长度；g为气隙有效长度。

由此可得：

(4)

Ls=Lms+Lσs

(5)

(6)

(7)

(8)

(9)

(10)

(11)

式中：i,j=1,2,…,n，j≠i且j>i。设：

(12)

(13)

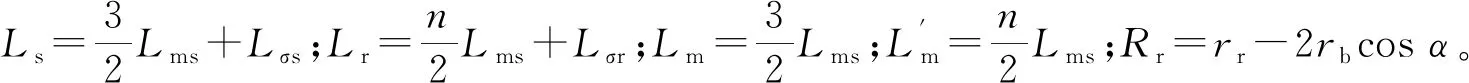
假设第j根鼠笼条断裂，则回路电流ij+1=ij，相当于把回路j和回路j+1合并成一个回路。为得到感应电机转子断条一根的多回路方程，由文献[20]可对式(1)和式(2)作如下处理：

(1) 电阻和电感矩阵的第j+4行元素和第j+4列元素分别加到第j+3行和j+3列对应的元素上；

(2) 删掉电阻和电感矩阵的第j+4行和第j+4列；

(3) 删掉电压、电流和磁链矩阵的第j+4行。

经过上述处理，可以得到感应电机转子断条数量为一根时的多回路模型方程。

(14)

以11 kW的电机Y160M-4为例，假设第13根鼠笼条断裂，对式(1)、式(2)和式(14)分别求解，将求解得到的电流和相应的电压做快速傅里叶分解，并将分解结果画成向量图,如图1～图4所示。

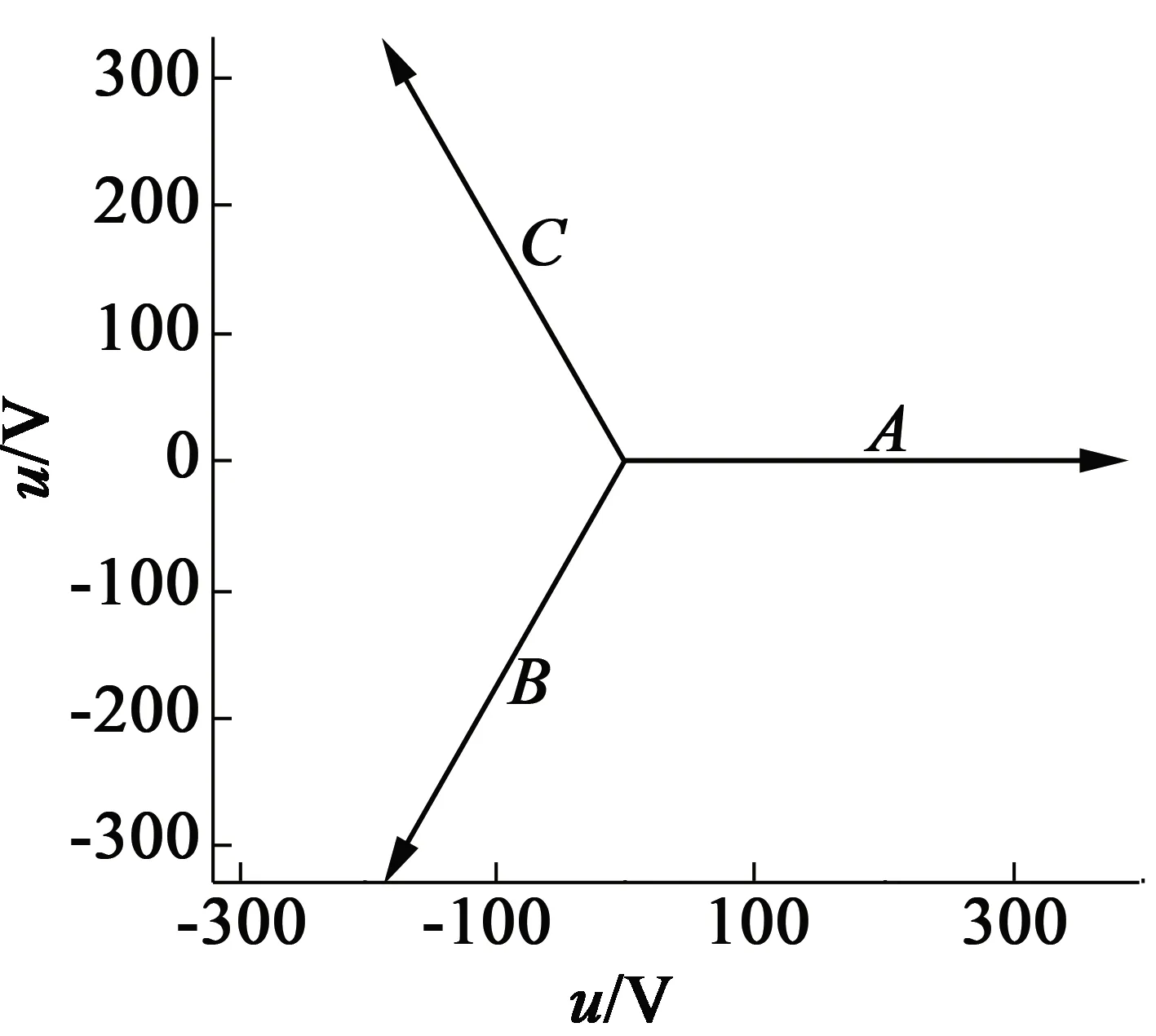
图1 正常电机定子三相电压向量图

图2 正常电机转子各回路电流向量图

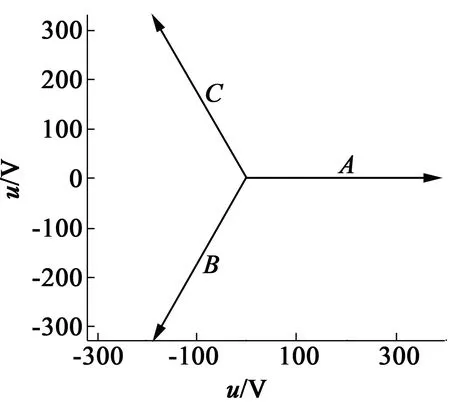
图3 断条电机定子三相电压向量图

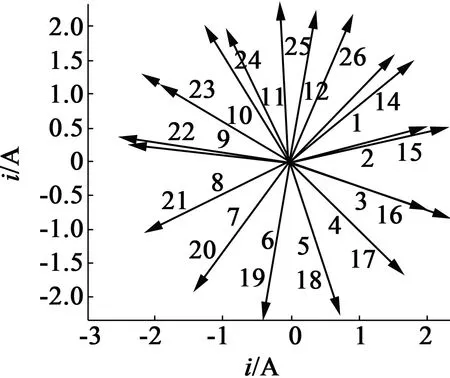
图4 断条电机转子各回路电流向量图

(15)

式中：q=1,2,3,…,n；θi为转子回路1轴线与定子a相绕组轴线重合时转子回流1电流的初相位；α为转子相邻回路轴线间的电角度。则有电机发生一根断条时各转子回路电流：

(16)

式中：q=1,2,…,n且q≠11,12,13,14；q1=12；α1为转子回路11和转子回路14 电流相位较正常时的变化量；k1为转子回路12电流幅值较正常时的变化系数；k2为转子回路11和转子回路14电流幅值较正常时的变化系数。

令电机发生一根断条的电流向量：

I1=[ia,ib,ic,i1,i2,i3,…,in]T

2 感应电机故障模型方程

设：

y1=(n-2)/2+cosα

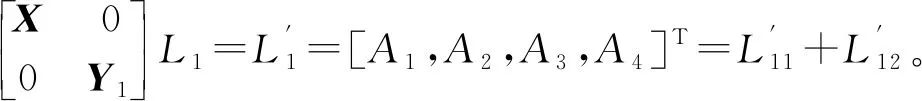
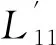
(17)

式中：q=1,2,…,n且q≠11,12,13,14，q1=12。则有：

(18)

式中：

I1r=[i1,i2,…,iq1-1,iq1,iq1+2,…,in]T

(19)

(20)

(21)

故可设：

令：

式中：B1=[b11,b12,b13,…,b1,n+3]，B2=[b21,b22,b23,…,b2,n+3]，B3=[b31,b32,b33,…,b3,n+3]，B4=[b41,b42,b43,…,b4,n+3]。

又有：

式中：q=1,2,…,n且q≠11,12,13,14，q1=12。

同理可得：

(22)

(23)

式中：

Lr1=y′(Lms+Lδr/y1)+ε3+ε4[cos(x)-sin(x)iqdr]

Lr2=y′(Lms+Lδr/y1)+ε3-ε4[cos(x)+sin(x)idqr]

[cos(x)-sin(x)iqdr]

[cos(x)+sin(x)idqr]

又有：

ε4=k2(Lms+Lδr/y1)[cos(3α-α1)-

idqr=idr/iqr

iqdr=iqr/idr

x=2(θ1-θr)-2(q1-1/2)α

以故障模型输出电流响应建立函数Fi，则有：

Fi=f(x,θu,rs,Rr,Lms,Lδs,Lδr,n,α,ωr)

(24)

对于一台具体的电机，其rs,Rr,Lms,Lδs,Lδr,n,α,ωr是确定量，此时有：

Fi,1=f1(x,θu)

(25)

式中：θu为输入a相电压初相角。

以实测电机电流Fi,real与Fi,1建立目标函数：

(26)

将x作为自变量，则在最优解时有：

x=g(θu)

(27)

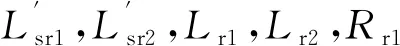
3 感应电机参数辨识

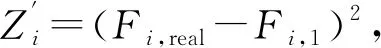
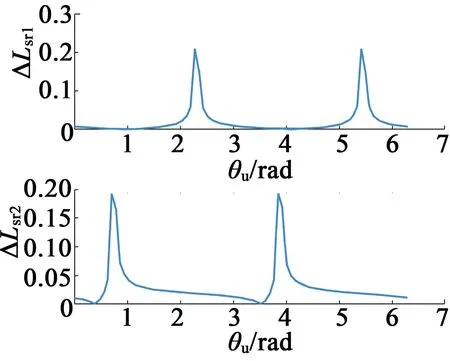
图的变化曲线

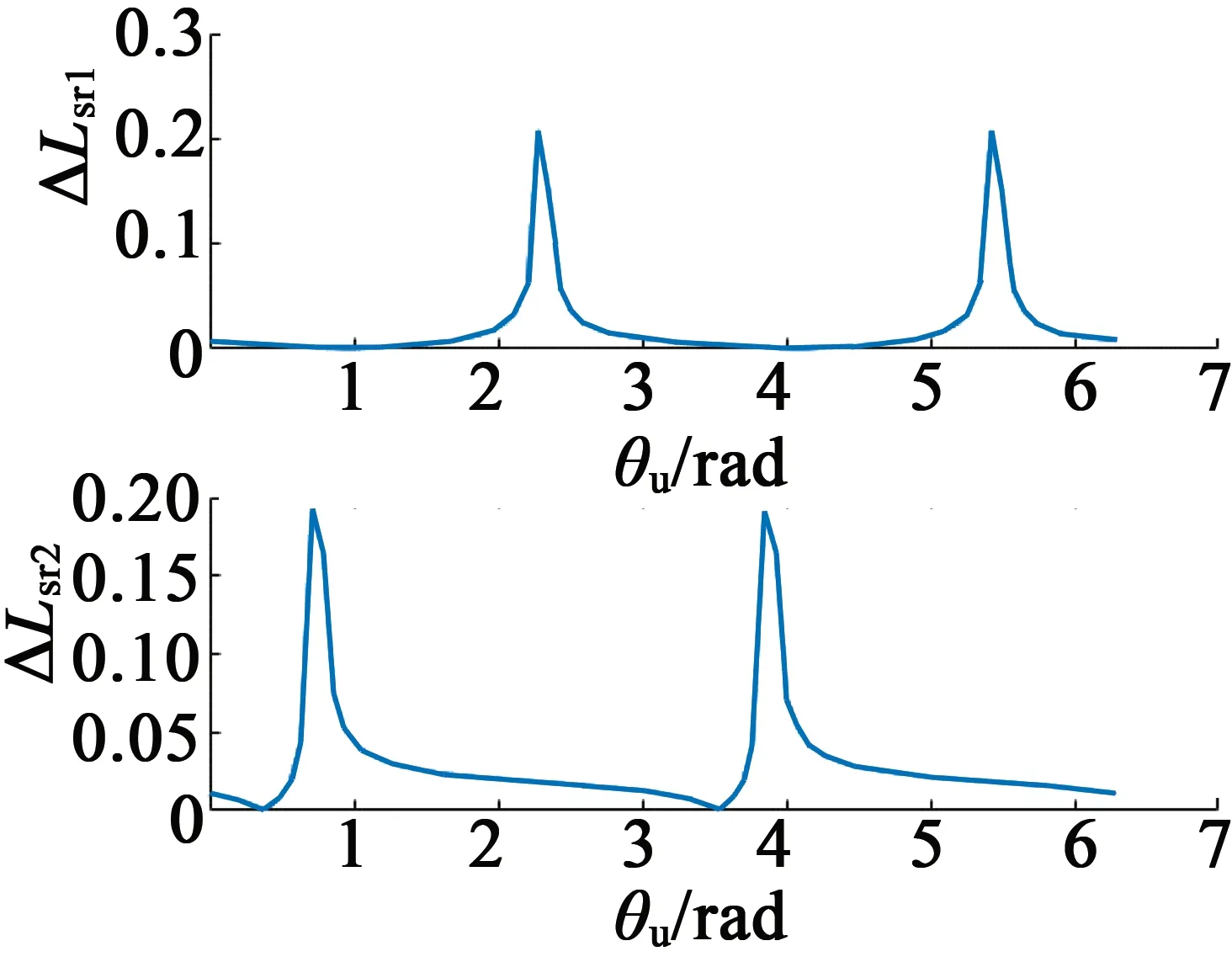
图6 Lr的变化曲线

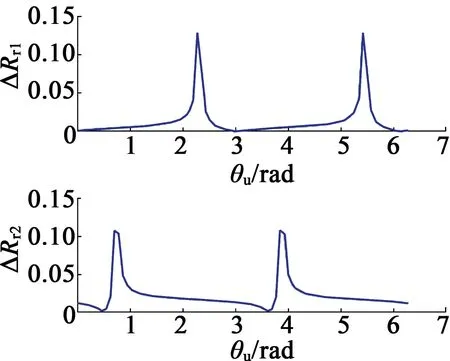
图7 Rr的变化曲线

因此，通过本文的建模方法，当电机发生断条故障时，利用参数辨识和滑窗技术相结合的方法可获取较明显的尖峰特征信号，可用于检测电机是否发生了断条故障。

4 结 语

本文针对感应电机发生一根断条的情况，以一台11 kW电机为例，论述了一种感应电机转子断条建模方法的过程和原理，该建模方法在与参数辨识和滑窗技术相结合后，可获取明显的感应电机转子断条故障特征信号，克服了感应电机发生早期断条故障时等效参数特征不明显的问题，可用于诊断感应电机转子断条故障。同时该建模方法也为利用信息融合技术进行电机故障诊断提供了一条路径。