采用稀疏测量数据的有限角度光声层析成像的研究进展
2020-03-23孙正闫向阳
孙正,闫向阳
(华北电力大学电子与通信工程系,河北保定071003)
0 引 言
光声层析(Photoacoustic Tomography, PAT)成像是一种基于生物组织光声效应的非电离功能成像方法,其成像参数是组织的光吸收系数和散射系数,可以实现高分辨率和高对比度的软组织深层成像[1],PAT 成像可用于冠状动脉粥样硬化性疾病、乳腺癌和消化系统病变等的早期诊断。
PAT 成像的灵敏度和分辨率取决于组织的光吸收对比度、激光脉冲持续时间、超声检测系统的几何结构和带宽以及图像重建算法等。其中高质量的图像重建是提高PAT 成像分辨率的重要途径,目前较为成熟的图像重建算法包括滤波反投影法(Filtered Back-Projection, FBP) 、 时 间 反 演 法(Time-Reversal, TR)、基于傅里叶变换的算法和代数迭代法等[2]。这些算法一般都需要对光声信号进行全角度的扫描测量,以得到完备的光声数据集。但是在实际应用中,特别是内窥式光声成像,如血管内光声成像[3],由于管腔内封闭成像几何的特殊性,并且受成像导管的机械结构、空间位置及成像时间等的限制,超声探测器往往只能在封闭的管腔内进行有限角度的扫描,导致采集到的光声数据不完备。而根据稀疏的光声测量数据精确计算未知光声信号的过程是不稳定的,难以求解其高频成分。本文对在有限角度扫描条件下,采用在稀疏位置测量的不完备光声信号重建PAT 图像的主要方法进行综述,讨论各方法的优势和不足,并展望未来可能的发展方向。
1 有限角度扫描PAT 成像
1.1 PAT 成像原理
PAT 成像原理示意图如图1 所示,采用短脉冲激光照射生物组织,组织吸收光能量后受热膨胀产生瞬时压力,并向外辐射宽带(带宽为10 kHz~100 MHz)超声波,即光声信号[1]。声压的幅值与脉冲激光的强度成正比,反映组织的光吸收特性。超声换能器接收来自不同方向、不同位置的光声信号,送入计算机后采用合适的算法即可反演得到组织内部初始声压的空间分布,进而得到空间光吸收分布图,直观显示组织的内部结构。在此基础上还可估算组织的光学特性参数(光吸收系数和散射系数)的空间分布,反映组织的功能成分,即定量PAT(Quantitative PAT, qPAT)[4]。
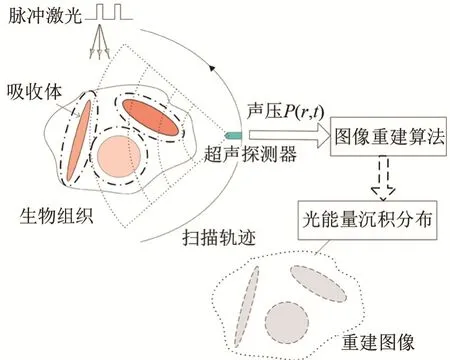
图1 PAT 成像原理示意图Fig.1 Schematic diagram of PAT imaging
1.2 有限角度扫描问题
目前,多数PAT 图像重建算法都需要对光声信号进行全角度的扫描测量(如二维圆周扫描),以获得完备的光声测量数据集。但在实际应用中,探测设备尺寸、机械结构和空间位置等会使超声换能器的扫描角度受限。有限角度PAT 成像的扫描方式主要包括两种类型:有限角度圆周扫描和直线扫描。此外,一些不规则的扫描几何,如未闭合的曲线扫描也属于有限角度扫描。由于投影的角度范围不能满足数据完备性的条件,因此会导致重建图像中出现严重的伪影和失真,降低图像质量。
此外,在某些应用中,受成像目标的几何形状、解剖位置、曝光时间和数据检测时间等的限制,超声探测器只能采集到不完备的稀疏光声数据。例如连续光声成像扫描,为了在不增加产品成本和保持高分辨率的同时加快数据采集速度,必须减少测量次数。稀疏测量会导致成像目标的重建图像沿着目标中心连线的方向扩散,并且扩散的区域随着扫描范围的减小而增大,导致图像模糊、细节缺失和伪影现象严重。若采用最小分辨间距来衡量重建图像的分辨率,采用扫描角度衡量扫描范围的大小,则最小分辨间距与扫描角度之间呈指数关系[5]:

其中:γ 是最小分辨间距;θ 是扫描角度;γ0是全方位扫描时的最小分辨间距;A 和B 是待定系数。
2 有限角度PAT图像重建的主要方法
对于有限角度扫描采集的不完备光声数据集,直接应用传统的图像重建算法会导致图像中存在盲区、模糊和伪影等问题。目前,用于有限角度稀疏测量数据的PAT 图像重建方法主要有:插值法、基于圆弧Radon 变换的方法、基于Gerchberg-Papoulis外推的补偿方法、迭代重建法、频域反卷积法、基于压缩感知的方法和基于深度学习的方法等。
2.1 插值法
针对由不完备数据造成的图像伪影现象,最简单的方法是插值法,即根据采集的光声信号,利用特定的插值函数计算出未测位置上的信号值,进而重建图像[2]。插值法重建结果对比如图2 所示,采用基于三维平面扫描的插值算法[6]可以提高合成的光声信号的准确性,降低计算成本。与常规的反投影法相比,它能够减小旁瓣和伪影,而且由于考虑了光的衰减,因此可以实现连续重建。插值法的精度一般不高,而且还需要解决声速不均匀问题和考虑超声探测器尺寸的影响。

图2 插值法重建结果对比[6]Fig.2 Comparison of reconstruction results with interpolation method[6]
2.2 基于圆弧Radon 变换的方法
基于圆弧Radon(Circular Arc Radon, CAR)变换的数值反演算法是一种高效的非迭代算法,它能够解决全圆周Radon 变换反演算法中第一类Volterra积分方程得不到稳定解的问题,其原理[7]是:首先,使用梯形积分(Trapezoidal Product Integration, TPI)法反演求解CAR 变换中出现的第一类Volterra 积分方程;然后采用截断奇异值分解(Truncated Singular Value Decomposition, TSVD)法对积分核的离散近似病态矩阵B 进行分解,得到其逆矩阵B-1;最后,利用CAR 逆变换得到原始声压分布。在有限角度扫描的情况下,由于圆弧边界混入大量伪影以及圆弧角度的限制,可能导致图像中一些目标的边缘不可见。为此,可对矩阵B 进行加权处理,以减少有限角度扫描造成的伪影。矩阵B 加权处理对重建结果的影响如图3 所示。

图3 矩阵B 加权处理对重建结果的影响[7]Fig.3 Effect of weighting B on the reconstruction results[7]
2.3 迭代重建算法
2.3.1 同步迭代重建算法
采用基于全变分(Total Variation, TV)的迭代重建算法可以大幅减少所需的测量数据,但是缺少某些角度的投影数据可能导致图像边缘模糊和明显的伪影,特别是在数据严重不足时[8]。此外,还可采用代数重建算法(Algebraic Reconstruction Techniques, ART),与FBP 相比,ART 可以显著提高图像的分辨率和对比度[9],但是其计算复杂度较高,一定程度上会影响重建的速度和质量。
为了解决上述问题,可采用同步迭代重建技术(Simultaneous Iterative Reconstruction Technique,SIRT)及其改进算法(Modified SIRT, MSIRT)[10-12]。同步迭代就是以各像素对应于所有迭代变化的平均值作为像素的修正值。SIRT 的原理是:首先,设定初始重建图像;然后,计算通过图像中各像素点的所有投影数据,以此修正图像;最后,检验是否满足收敛准则。ART 和SIRT 的重建时间如表1 和图4 所示,相较于ART,SIRT 的迭代收敛速度更快,能够以较少的迭代次数实现高精度的图像重建,但重建时间较长。为此,需对SIRT 进行改进。
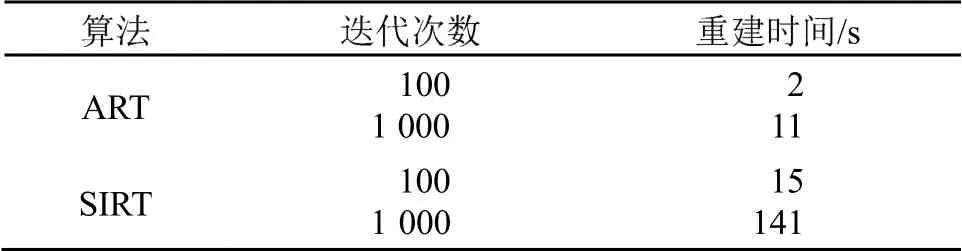
表1 ART 和SIRT 的重建时间对比[12]Table 1 Comparisonof reconstruction time of ART and SIRT[12]
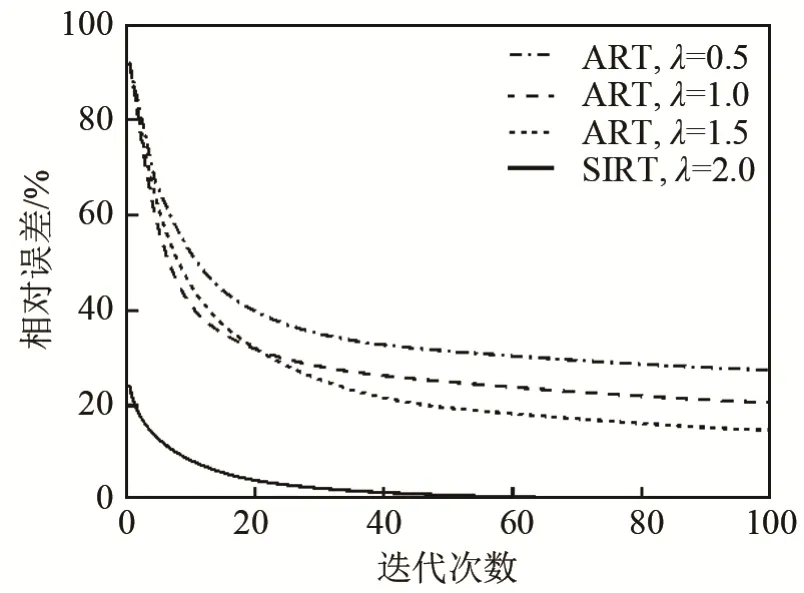
图4 ART 和SIRT 的收敛速度比较(λ 为松弛因子)[12]Fig.4 Comparison of convergence speed between ARTand SIRT (λ is the relaxation factor)[12]
MSIRT 方法中每次迭代的是各像素的修正值,即累加经过该像素的所有投影数据的误差值,而不是只与一条投影数据有关,可有效抑制测量数据中的噪声。此外,通过线性搜索调整速度更新的步长,还可以提高迭代收敛的速度[13],ART 和MSIRT 的性能和重建结果分别如表2 和图5 所示。

表2 ART 和MSIRT 的性能对比[13]Table 2 Comparison of performance of ART and MSIRT[13]

图5 ART 和MSIRT 的重建结果对比[13]Fig.5 Comparison of reconstruction results with ART and MSIRT[13]
2.3.2 与FBP 结合的迭代重建算法
(1) 结合有限域FBP 的实时迭代重建方法
FBP 的原理简单、速度快且易实现。但对于有限角度扫描获得的不完备数据,FBP 会导致图像的空间分辨率和对比度降低,使目标的形状发生模糊和变形。与FBP 相比,SIRT 可以大大减少重建图像中的伪影,并在数据不完整以及含有噪声的情况下重建更高质量的图像,但其计算复杂度较高,所需的计算时间远大于FBP,可能会限制其在实时成像中的应用。通过将SIRT 与有限域FBP 相结合,则可在保证重建精度的基础上,显著减少重建时间。其原理是:首先利用有限域FBP 重建初始图像,然后使用SIRT 对初始图像进行优化[14],结果如图6所示。另外,对于换能器阵列接收立体角有限的问题,则可将换能器阵列的方向性模式函数作为迭代过程中的加权因子,以进一步改善图像质量。

图6 与有限域FBP 相结合的SIRT 重建结果[14]Fig.6 Results of SIRT combined with FBP in limited-view[14]
(2) 组合迭代重建算法

图7 3 种算法的重建结果对比Fig.7 Comparison of reconstruction results of three algorithms[15]
(3) 迭代加权FBP 算法
迭代自适应加权 FBP(Iterative Adaptive Weighted FBP, IAWFBP)[16]的原理是:首先,利用基于有限角度的FBP 重建初始图像;然后,根据初始图像和光声信号测量值计算投影信号的加权系数;其次,利用初始图像和加权系数得到模拟的光声信号,并计算其与测量值之间的残差;最后,对残差信号做反投影运算得到残差图像,并将其与上一次迭代生成的光吸收分布图相加获得修正图像。重复上述过程,并设置最大迭代次数和迭代误差作为迭代结束条件。FBP、ART-FBP 和IAWFBP 算法的性能对比如图8 所示。IAWFBP 方法可以有效减少图像中的伪影,且在精度、对比度和对噪声的鲁棒性等方面都有很好的表现。但是,该算法存在成像系统扫描时间过长的缺陷,可以使用多阵元探测器阵列和多光谱高频激光源减少扫描时间。
采用正则化迭代加权FBP(Regularized Iterative Weighted FBP, RIWFBP)[17]还可进一步提高重建精度。首先,使用FBP 从有限角度测量数据中重建初始光吸收分布图;然后,在每一次迭代中,计算光声信号的测量值和模拟值之间的差值,以此修正图像,并采用正则化方法提高迭代的收敛速度。实验证明,采用该算法在前五次迭代中即可有效抑制IAWFBP 中存在的有限角度扫描所致的伪影。而且该方法在精度和对噪声的鲁棒性方面均优于IAWFBP 和传统的迭代方法,能够显著减少所需的超声换能器数量和扫描时间,IFBP、IAWFBP、RIWFBP 算法的性能对比如图9 所示。

图8 FBP、ART-FBP 和IAWFBP 算法的性能对比[16]Fig.8 Comparison of FBP, ART-FBP and IAWFBP[16]
(4) 滤波平均反投影迭代算法
FBP 是将去除探测器脉冲响应的光声信号测量值直接反投影到对采集信号有贡献的测量点上,会造成不同位置测量点的投影不均匀现象。利用滤波平均反投影算法可解决该问题[18]:首先,对光声信号测量值进行反卷积去除探测器脉冲响应的影响,统计对采集信号有贡献的投影点个数,求得实际光声信号均值,并将平均后的信号对每一个测量点进行反投影重建;然后,对成像区域中每一点的像素值用该点的投影累加次数进行平均。采用该方法重建的初始声压分布图的结构与实际的声场分布结构大致相同,各点的声压幅值和实际值较接近。

图9 IFBP、IAWFBP 和RIWFBP 性能对比[17]Fig.9 Comparison of performance of IFBP, IAWFBP and RIWFBP[17]
在传统的迭代重建中,声压分布的初始值通常采用空矩阵或者直接反投影的结果,可能增加迭代次数,延长计算时间。滤波平均反投影迭代(Filtered Mean-Back-Projection Iterative, FMBPI)算法[19]能够弥补传统迭代算法在计算时间上的不足,其原理是:首先,利用滤波平均反投影算法从不完备的光声数据中重建初始声压分布,作为迭代的初始值;然后,采用迭代重建算法修正初始声压分布,减小光声信号的计算值和测量值之间的误差,去除由反投影引入的伪影,FBP 和FMBPI 结果对比如图10所示。FMBPI 算法的适应性较强,由于采用滤波均值反投影算法对光声信号进行预处理,因而可以消除反投影的不均匀现象。另外,相对于传统的迭代重建算法,FMBPI 利用初始声压分布与实际分布之间的逼近关系以及权重因子来减少迭代次数,可以在相对较短的时间内重建出精度更高的光声图像。
牛肚菌。牛肚菌生长于海拔900-2200米的松树混交林中或砍伐不久的边缘地带,多产于云南省。牛肚菌香甜可口、营养丰富,中医认为其具有养血和中、祛风散寒、舒筋活血等功效,是妇科良药,同时还有抗流感、治感冒的作用。
2.3.3 基于梯度投影的迭代算法
基于稀疏探测器阵列和迭代重建算法的PAT成像系统为高帧率三维PAT 成像的开发提供了可能性,应用基于梯度投影的迭代图像重建算法[20]可以提高成像效率,获取以单束激光作为光源、帧率为10 Hz 的三维PAT 图像(图11)。该算法的原理是:首先,设定解的初始值;然后,由约束条件确定初始值的凸约束集边界上梯度的投影,求出可行的下降方向和步长;接着,线性搜索最优步长,并以此为条件求得新的迭代点;最后,进行收敛测试,检验是否可以终止迭代。

图10 FBP 和FMBPI 结果对比[19]Fig.10 Comparison of reconstruction results with FBP and FMBPI[19]

图11 SIRT 和基于梯度投影的迭代算法的重建结果对比[20]Fig.11 Comparison of reconstruction results with SIRT and gradient projection-based iterative algorithm[20]
2.4 基于Gerchberg-Papoulis 外推的补偿方法
由信号f(t)的部分已知数据g(t)重建f(t)在整个定义域上的值称为带限函数外推问题。Gerchberg-Papoulis(GP)外推算法是解决带限函数外推问题的一种迭代算法[21],其理论依据是长球面波函数展开及其相关的谱估计理论[22]。用GP 外推算法可解决有限角度PAT 成像中由不完备采样数据造成的盲区、模糊和伪影等问题[8]。首先,利用快速傅里叶变换得到光声信号测量值的频谱,在频域中做反投影运算,再利用傅里叶逆变换得到初始声压分布,进而求出空间光吸收分布,以此作为迭代的初始值;然后,利用GP 外推算法对盲区信号进行补偿,以修正图像,同时结合全变分(Total Variation, TV)正则化提高迭代的收敛速度。与迭代重建再投影(Iterative Reconstruction Reprojection, IRR)算法相比,该算法可以加快补偿速度,减少计算时间,解决稀疏探测器阵列采集信号所导致的伪影、失真和模糊问题,增强图像边缘,更好地保留细节信息,3 种算法的性能对比如图12 所示。
2.5 基于压缩感知的方法
2.5.1 压缩感知重建算法
压缩感知(Compressed Sensing, CS)理论打破了奈奎斯特抽样定理的限制,认为只要信号是稀疏的或可压缩的,就能够通过数据压缩节省对大量无用信息的采样,然后求解特定的优化问题,即可利用少量的压缩数据恢复原信号。
实际人体组织中,多数光吸收体的时空相关性较低,所以常规的采样数据通常是高度冗余的。由于大部分光声图像具有稀疏性,或者针对某个变换基函数满足稀疏性条件,因此利用少量随机采样信号能够实现图像的重建。即把原始光声信号在特定测量矩阵上的投影作为测量数据,通过稀疏约束重构算法恢复原始信号,最终利用少量数据和低成本硬件实现高分辨率光声成像[23]。

图12 TV-GD, TV-VB, TV-GPEF 算法的性能对比[8]Fig.12 Comparison of performance for TV-GD, TV-VB,TV-GPEF[8]
例如:在文献[24]中提出了一种基于CS 的光吸收分布图重建方法,利用全采样光声数据的1/4即可重建光吸收分布图。其原理是:初始光吸收分布通常由组织边界的光滑部分和跳变点构成,所以其拉普拉斯变换是稀疏的(或者至少是被压缩的)。根据光声信号测量值的二阶时间导数与初始光吸收分布的拉普拉斯变换之间的对应关系,重建出光吸收分布图[25]。针对脉冲激光随机照射条件下的PAT 成像,文献[25]提出利用CS 算法减少随机照射次数来提高数据采集速度,仅利用两个夹角为90°的探测器采集的信号测量值就能精确地重建光声图像。
此外,激光脉冲的重复频率和超声换能器的数量会限制光声信号的采集速度。通过采用线性集成探测器进行多角度扫描,设置合理的探头分布角度以及测量矩阵等,可以提高信号的采集和处理速度,有效弥补远场成像分辨率,消除图像伪影[26]。而CS 重建算法可以压缩采样数据,减少超声换能器的数目,加速数据采集,降低硬件成本[27],其图像重建效果优于反投影(Back-Projection, BP)和迭代重建[27-28],如图13 所示。另外,在提高对比噪声比(contrast-to-noise ratio, CNR)和重建速度等方面,频域CS 比时域CS 更具优势[29]。
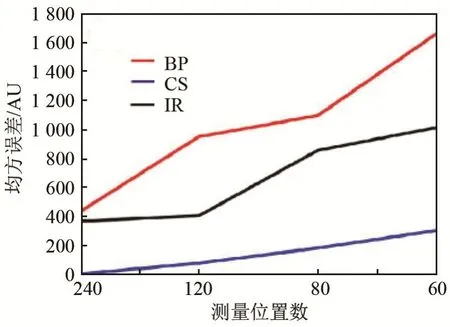
图13 反投影、迭代重建和CS 重建算法的性能对比[27]Fig.13 Comparison of performance of BP,IR and CS[27]
2.5.2 改进的压缩感知重建算法
(1) 结合快速交替方向法的压缩感知算法
在使用CS 算法重建图像的过程中,利用快速交替方向法(Fast Alternating Direction Method,FADM)可以很好地求解L0-正则化问题。首先,利用变量分裂技术将稀疏信号的L0-正则化问题转化为约束优化问题;然后,采用一步Gauss-Seidel 的思想,利用乘子函数对优化问题中的变量做极小化处理;其次,二次更新变量和乘子;最后,利用反正交变换重建原始信号。与FBP 和其它CS 算法相比,FADM 可以更快地减小相对误差,在计算效率和数据保真方面效果理想。此外,该算法对噪声有很好的鲁棒性[31-32],FBP 算法与FADM 重建结果的对比如图14 所示。
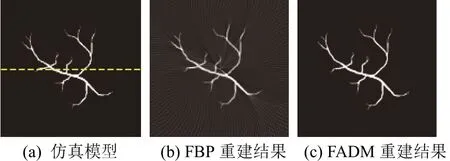
图14 FBP 算法与FADM 重建结果的对比[30]Fig.14 Comparison of reconstruction results with FBP and FADM[30]
(2) 具有部分已知支集的压缩感知算法
具有部分已知支集的 CS(CS with Partially Known Support, CS-PKS)算法[32-35]是将部分已知信号的空间位置作为CS 重建中的先验信息,降低待重建信号的复杂度。与传统CS 算法相比,CS-PKS可以用稀疏欠采样数据的1/3 重建具有更高CNR 的图像,减少高保真重建所需的测量次数,并能够以相对较少的迭代次数快速收敛,传统CS 方法与CS-PSK 方法对人手血管的成像结果如图15 所示。
(3) 合标准重建方法的压缩感知算法

图15 人手血管的PAT 图像[33]Fig.15 PAT images of the subcutaneous vasculature of human hand[33]
目前的三维PAT 成像系统能够实现高帧率的成像,但不能同时提供高空间和时间分辨率的图像,这限制了其动态成像(即四维PAT)的能力。结合标准重建法的CS 算法为解决这一问题提供了可能[25,37]。原理是:采用CS 算法从空间欠采样的光声信号中恢复完整的光声信号,然后利用标准重建算法重建图像。此外,还可通过结合TV 正则化方法,加速迭代收敛。这种复合算法能够减少空间测量次数,降低算法的复杂度,重建出具有较好空间分辨率和对比度的图像,反投影法和结合反投影的CS 重建结果如图16 所示[37]。
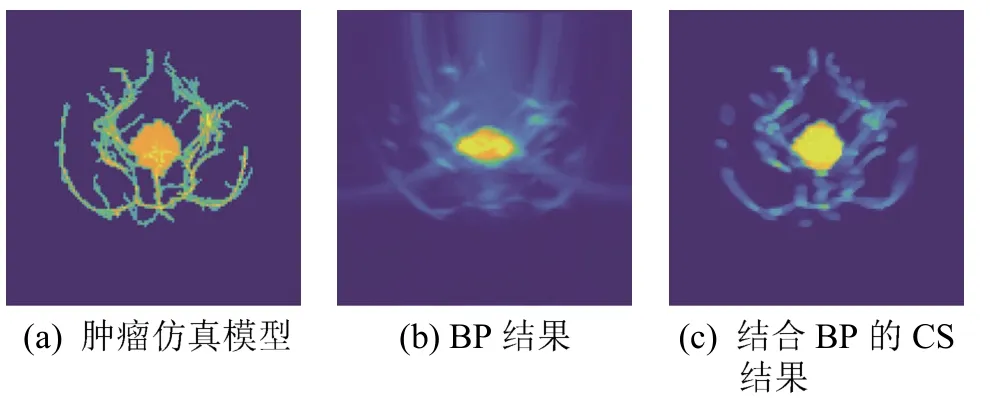
图16 反投影法和结合反投影的CS 重建结果[36]Fig.16 Reconstruction results with BP and CS combined with BP[36]
2.6 基于主成分分析的方法
主成分分析(Principal Component Analysis,PCA)是一种常用的统计方法,可以将高维数据空间转化为低维特征空间,在去除冗余、特征提取以及数据压缩等方面效果显著[37],已被广泛应用于图像处理、基因数据挖掘和医学成像系统中[38-41]。
基于PCA 的三维光声层析(PCA-PAT)成像[42]使用部分全采样数据来计算全部数据的主要成分。将一些均匀分布的全采样图像作为PCA 的训练样本,通过导出的PCA 数据恢复其它稀疏采样的图像,无需迭代过程便可根据稀疏采样数据快速重建高质量的三维光声图像。
PCA-PAT 成像是一种低成本的快速三维成像方法,可以有效地降低数据采集和图像重建的时间,与BP 相比,测量次数可减少约50%。在重建时间缩短约40%的情况下,可重建出与基于全采样的BP 质量相同的图像。另外,当超声换能器数量相同时,PCA 的图像重建速度约是CS 的8 倍,且成像精度更高,分别如表3 和图17 所示。
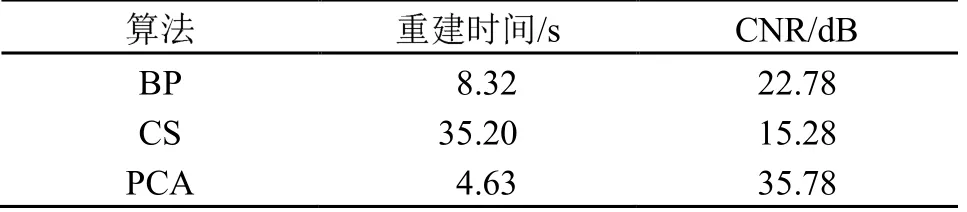
表3 BP,CS 和PCA 算法重建时间的比较[42]Table 3 Comparison of reconstruction time of BP, CS and PCA methods [42]

图17 应用BP、CS 和PCA 的重建图像[42]Fig.17 PAT images reconstructed with BP, CS and PCA methods[42]
2.7 基于深度学习的方法
深度学习(deep learning)是机器学习中对数据进行表征学习的一种方法,在模式识别和机器学习领域具有广泛的应用。近年来,深度学习算法特别是卷积神经网络(Convolutional Neural Network,CNN)已经迅速成为医学图像分析的首选方法[43],它在快速重建高质量的图像方面也具有巨大潜力。针对稀疏采样的PAT 成像,通过将CNN 与标准重建方法相结合,可以得到高分辨率的光声图像[44]。与经典的迭代重建算法相比,基于CNN 的重建算法在速度和质量等方面也具有较大优势。
基于CNN 的PAT 图像重建算法可以分为两类:(1) 首先采用快速、简单的标准重建算法从稀疏采样的光声数据中重建出含有伪影的低质量图像,然后用训练后的CNN 进行图像后处理,去除伪影[45-46],重建结果如图18 所示;(2) 基于模型的深度学习,即将PAT 成像的前向物理模型包含到CNN 的训练和图像重建中。例如文献[44]提出的方法将稀疏光声数据的梯度信息和迭代算法相结合,首先计算光声信号测量值的梯度,通过训练使CNN 学习目标图像的先验知识(如结构特点等);然后,将训练后的CNN 应用于光声测量数据,并使用迭代算法重建光声图像,重建结果如图19 所示。
相对于点探测器,采用集成线性探测器可实现对三维结构的高分辨PAT 成像。最近,使用64 个并行线性探测器阵列的三维PAT 成像系统也已实现[47]。针对此类系统,将动态孔径长度(Dynamic Aperture Length, DAL)校正算法与CNN 方法相结合,能够实时生成高分辨率的三维投影图像[48]。
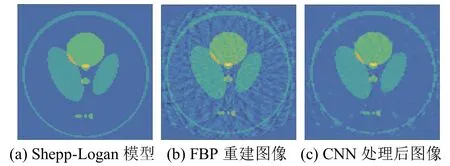
图18 CNN 后处理的重建结果[45]Fig.18 Reconstruction results of CNN post-processing[45]
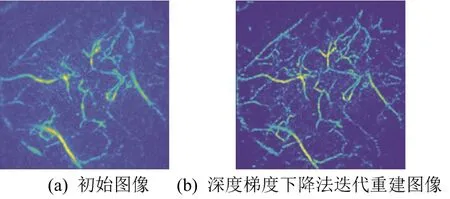
图19 人手掌的光声图像[44]Fig.19 The photoacoustic tomography of a human palm[44]
3 有限角度定量光声层析成像
对于有限角度扫描的多光源 qPAT (Multiple-Source, MS-qPAT),不完备的测量数据会导致无法稳定重建初始声压分布,故传统的两步算法[4]不再适用。此时可采用一步算法[49],即利用多个光源照射得到的多组声压数据直接重建光吸收系数和散射系数。例如,文献[50-51]提出一种实用的MS-qPAT 图像重建方法,首先确定超声换能器的空间冲激响应(Spatial Impulse Response, SIR)和声电冲激响应(Acousto-Electric Impulse Response, EIR),模拟声学测量;然后,采集光源附近区域的声压信号,在光声耦合前向传输模型中结合空间SIR、EIR以及有限角度扫描,利用基于交替方向法(Alternating Direction Method, ADM)的拟牛顿法获得光吸收系数和散射系数的精确解。
4 结 语
PAT 成像的效率和图像质量与图像重建算法有直接的关系。目前,多数成熟的标准重建算法都是基于完备数据的,但在实际应用中受探测器阵元尺寸、机械结构、接收角度以及带宽等的限制,往往不能满足全角度扫描和完备数据采集的条件。若仍采用标准重建算法,则可能导致图像中的伪影严重,空间分辨率降低。近些年,针对有限角度扫描和稀疏测量数据的问题,各种新的图像重建算法层出不穷。这些算法能够利用高度不完备的测量数据恢复高质量的图像,它们对扫描角度和数据稀疏度的要求如表4 和表5 中所示。
减少测量次数、降低系统成本、提高数据采集速度和成像速度是今后PAT 研究的主要发展方向,这对于实现三维光声图像重建以及高性能、高分辨率和高性价比的PAT 成像系统开发具有重要意义。

表4 主要算法的有效扫描角度范围Table 4 Effective angle range of the algorithms mentioned in the paper
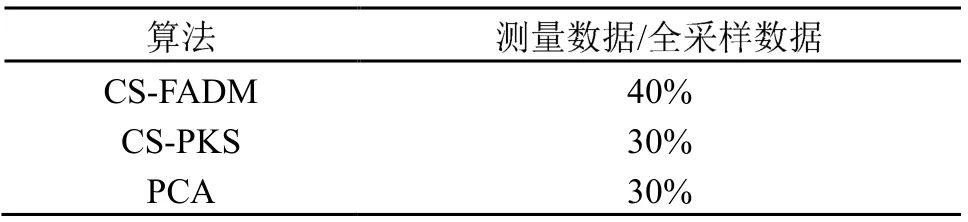
图5 主要算法的数据稀疏情况Table 5 The sparse data of the algorithms mentioned in this paper
