功能梯度压电层/压电半空间结构中Love 波的传播:一种改进的拉盖尔多项式方法
2020-03-23张朋威禹建功张小明
张朋威,禹建功,张小明,张 博
(河南理工大学机械与动力工程学院,河南焦作454000)
关键字:功能梯度材料;拉盖尔多项式;Love 波;位移分布;应力分布
0 引 言
功能梯度压电材料(Functionally Graded Piezoelectric Materials, FGPM)可实现机械能与电能的转化,通过调整材料组成使其梯度化,可使压电系数获得最恰当分配以达到提高压电器件性能及寿命的目的,被广泛应用于电气、机械、通信、光学、核能、化学、生物医学和土木工程等领域。而Love 波作为水平剪切(Shear Horizontal, SH)波的一种,其剪切极化和声能量集中在表面附近的几个波长以内,可以利用Love 波的这种特性与压电材料来制作Love 波传感器[1],Love 波传感器是通过在水平切变表面波器件表面覆盖薄层波导及超薄金属催化膜得到,其声波能量集中在薄层波导内,因此Love 波传感器能非常敏感地反映环境的扰动与变化。而Love 波在不同结构中传播特性的研究可为Love 波传感器研制提供理论依据[2]。因此,越来越多的国内外学者使用不同的方法和模型研究了FGPM 半空间结构中Love 波的传播特性。例如WKB 法[3]、贝塞尔函数法[4]、幂级数法[5]、刚度矩阵法[6]及正交多项式方法[7]等。
正交多项式方法于1972 年由Maradudin 等[8]提出,并使用拉盖尔多项式方法研究了半无限体中的波传播;之后,该方法被用来解决各种波和振动的问题,从均匀和层状结构中的表面波[9]到非均匀半空间结构中的表面波[10]。该方法有两个主要特点:(1) 利用正交多项式扩展的每个位移分量来计算整个空间的运动方程,将运动方程转化为矩阵求解特征值问题;(2) 通过假定与位置有关的材料常数可直接把边界条件纳入到运动方程中,极大地简化了边界问题的处理过程。
传统的拉盖尔多项式方法用一种展开的多项式处理波传播问题,只能确保位移和电势在整个结构中是连续的,但由于两个相邻层的材料常数不同,必将产生不连续的应力和电位移分布。为了克服此方法的不足,本文提出了一种改进的拉盖尔多项式方法。对于有限厚度的覆层,该方法将位移展开成勒让德多项式级数,而在相对无限的半空间基体,将位移展开成拉盖尔多项式级数。与传统拉盖尔多项式方法对比,该方法能够得到连续的正应力和正电位移分布。分析了覆层梯度变化和波数变化对Love 波波动特性的影响。
1 基本方程及求解
基于三维线性压电弹性理论,考虑一个带有功能梯度压电覆层的压电半空间结构,其上表面自由,覆层厚度为h。采用笛卡尔坐标系(x, y, z),如图1 所示,原点设在材料的表面,材料的极化方向垂直于xOy 平面,波的传播方向为y 方向,质点的振动方向为z,半空间的厚度方向为x 轴的正方向,覆层材料特性在厚度x 方向上发生梯度变化。
对于压电但无磁化的电介质体,线性压电的波动控制方程由式(1)中的运动方程和麦克斯韦方程组成:

本构方程和压电方程分别为

几何方程为
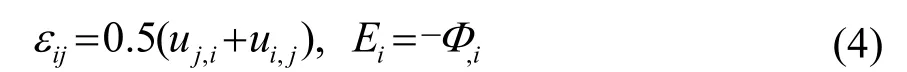
式(1)~(4)中:Tij和εkl分别应力和应变;Di和 Ek分别为电位移和电场强度;Φ 为电势;ui为位移;Cijkl为弹性常数;ekij和∈ik分别为压电常数和介电常数;ρ 为材料密度,下标中逗号表示对坐标的偏微分。
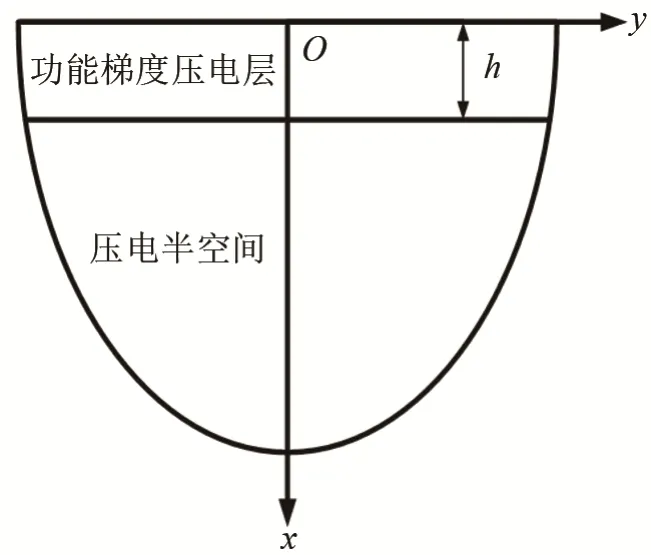
图1 带有功能梯度压电覆层的压电半空间结构Fig.1 Schematic diagram of piezoelectric half-space covered by a functionally graded piezoelectric layer
假设Love 波沿y 方向传播,位移和电势可表示为
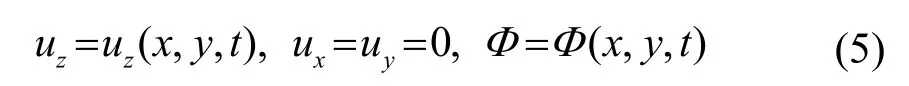
将式(5)代入式(1),可得到式(6)的运动方程:

功能梯度压电材料的本构方程可写为
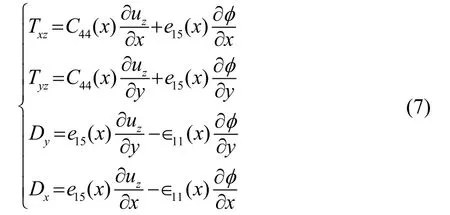
考虑应力自由、电开路的边界条件(Txz=0,Dx= 0,x=0 和x→∞处),引入矩形窗函数θ (x):

此函数的引入,直接在波动方程中解决了结构的边界条件问题,具体证明见文献[11]。
对于覆层,材料常数被写成式(9)的形式:
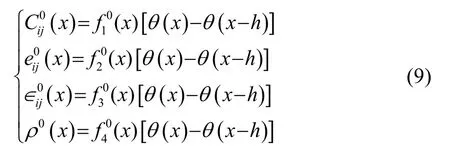
在半空间基体,材料常数可表示为
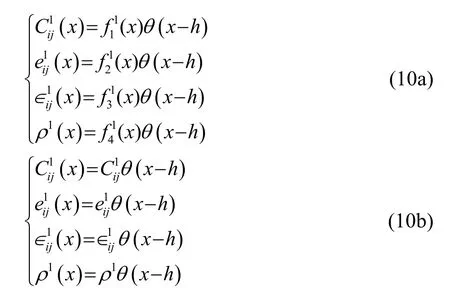
对于带有覆层的压电半空间结构,Love 波的自由谐波解可以表示成如下形式:
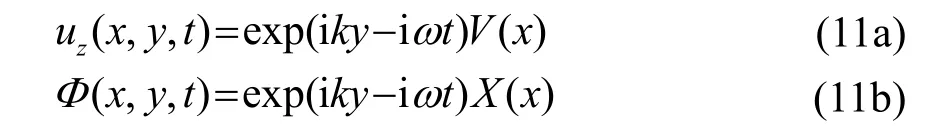
式中:k 为波数;ω 为波的角频率;V ( x) 为z 方向的振幅;X ( x )为电势振幅。
将式(7)~(9)和式(10)~(11)代入式(6),则得到位移、电势表示的波动控制微分方程:
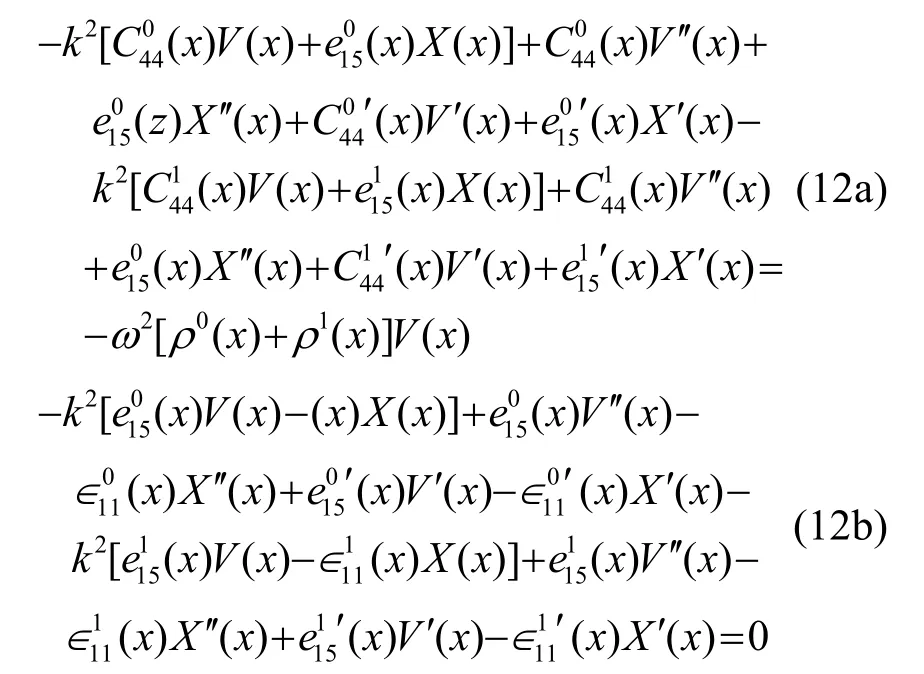
式中,上角标'和"表示对x 的一阶和二阶导数。
为了求解波动控制微分方程,传统的拉盖尔多项式方法把位移分量V(x)和X(x)都扩展成拉盖尔多项式级数来处理层状半空间结构。
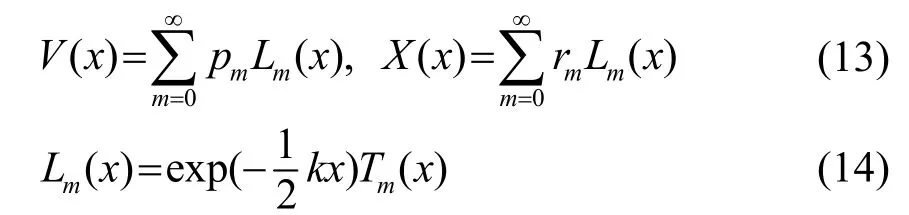
式中: pm、rm是待定多项式系数;Tm( x) 是第m 阶拉盖尔多项式。
当两个相邻层的材料常数不同时,传统拉盖尔多项式方法只能保证连续的位移和电势分布,必将产生不连续的应力和电位移分布。因此,本文提出一种改进的拉盖尔多项式方法来处理带覆层的半空间结构。在覆层,将V(x)和X(x)展开成勒让德多项式级数,在半空间基体,将V(x)和X(x)展开成拉盖尔多项式级数。
在覆层:
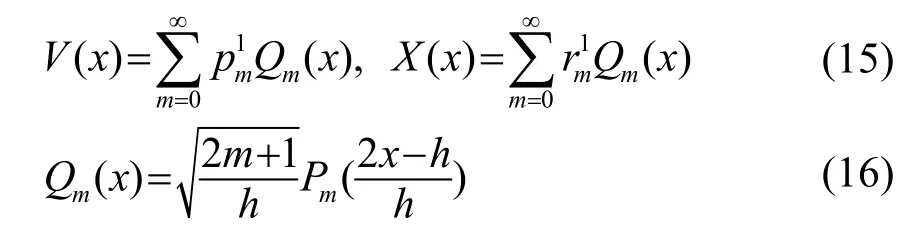
在半空间基体:
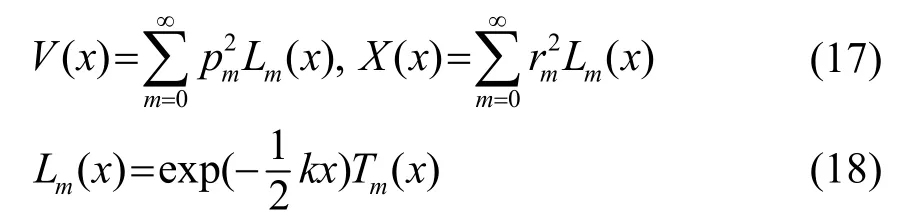
为了满足界面处应力和电位移连续,位移和电势表示为
在覆层:
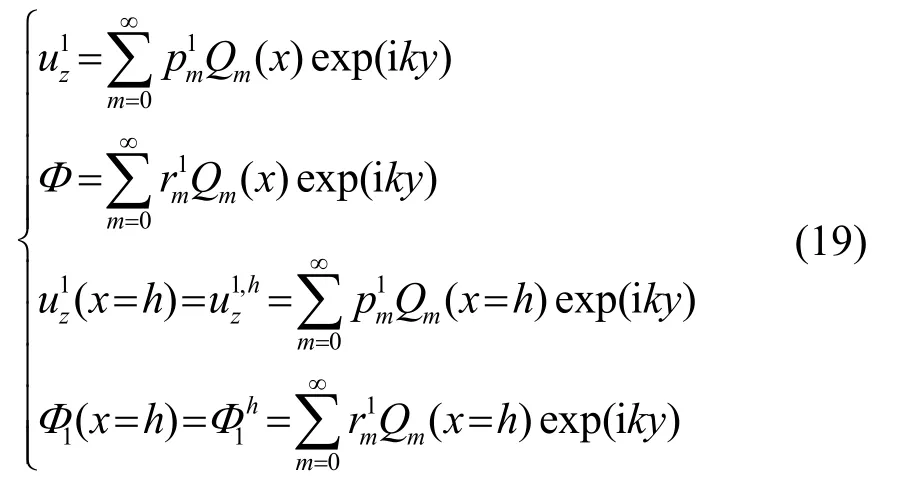
在半空间基体:
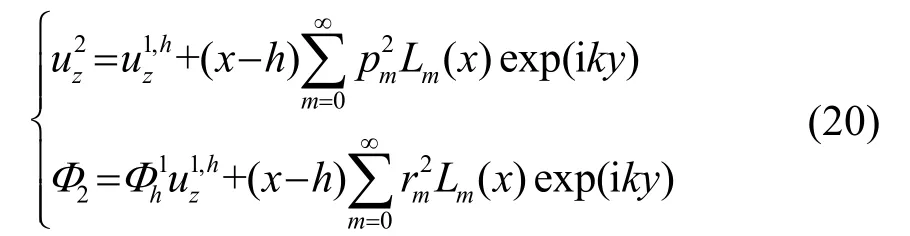
把式(16)~(20)代到式(12)中,两边同时乘以Qj( x) 、 Lj( x),j 从0~M,然后对x 从0~∞求积分,可以得到如式(21)的代数方程:
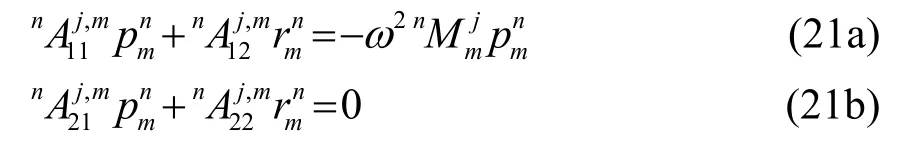
把式(21b)写成:

将式(22)代入式(21a)得:
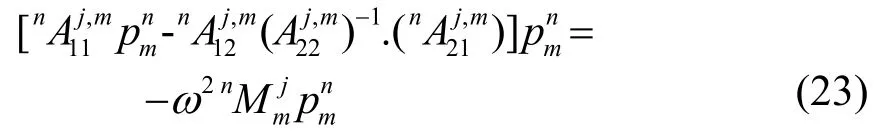
式(23)也可以表示为
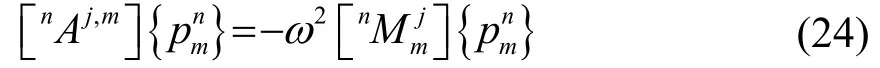
2 数值算例及讨论
在覆层,假设梯度材料有2 种组分组成,在计算FGPM 的等效参数时,使用混合率细观力学模型,即:
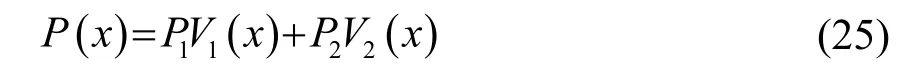
这里Pi和Vi(x )分别代表第i 种材料的材料特性及体积含量,其中V1(x ) + V2(x)=1 ,由此可得:
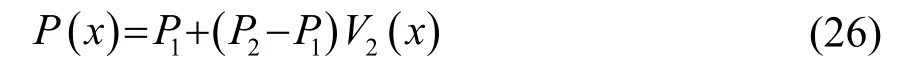
梯度结构在厚度方向的组分变化规律可表示为
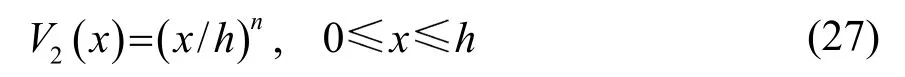
在半空间基体,假设材料是均匀的。
基于上述理论,分别开发了基于改进的拉盖尔多项式方法和传统的拉盖尔多项式方法的Mathematica 程序,计算了带有功能梯度压电覆层的压电半空间中Love 的波频散、应力和电位移曲线。
为了验证所提出方法的正确性,首先计算了带有均匀压电覆层的压电半空间中Love 波频散曲线,并与文献[1]中WKB 法得到的频散曲线结果进行比较。所用的材料参数可在文献[1]找出。计算结果如图2 所示,其中点线为改进的拉盖尔多项式方法得到的结果,实线为WKB 方法得到结果。由图2 可以看出,两者的计算结果吻合。
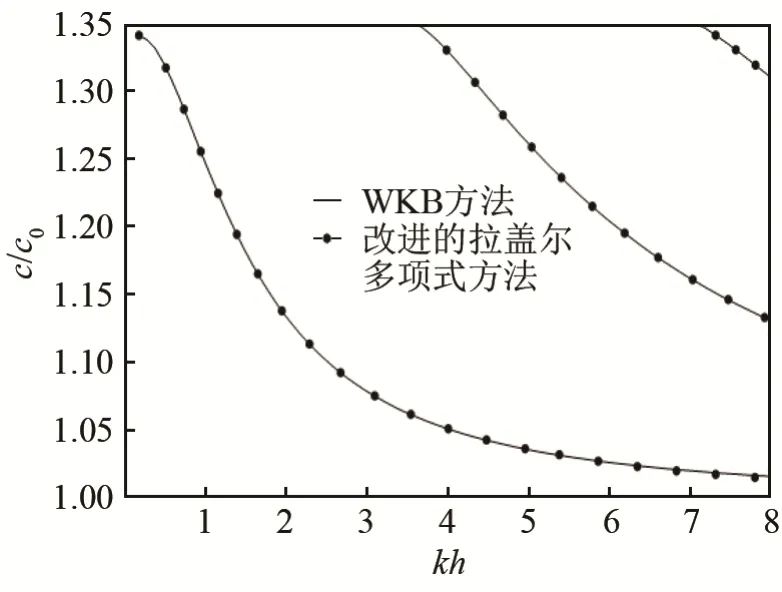
图2 带有均匀压电覆层的压电半空间中Love 波频散曲线Fig.2 Dispersion curves of Love waves in a piezoelectric half-space covered by a homogeneous piezoelectric layer
带有功能梯度压电覆层的压电半空间结构,覆层上表面即x=0 处的材料为PZT-2,覆层下表面x=h=1 mm 处选用材料PZT-4,压电半空间材料选用BaTiO3,简写为PZT-2/PZT-4/BaTiO3。相关的材料参数如表1 所示。梯度场函数选用这里n 分别取1、2 和3,
所得Love 波的频散曲线如图3 所示。可见,随着梯度场函数的变化,即幂函数幂n(以下称梯度指数n)的增加,Love 波的相速度变小,频散越显著。由方程(27)可知,随梯度指数n 的增加,覆层上表面材料的体积含量增加。而PZT-2 材料体波波速小于PZT-4 材料的波速,因此,随着梯度指数n 的增加,Love 波的相速度值变小。

表1 计算所用的材料参数Table 1 Material parameters used in the computation
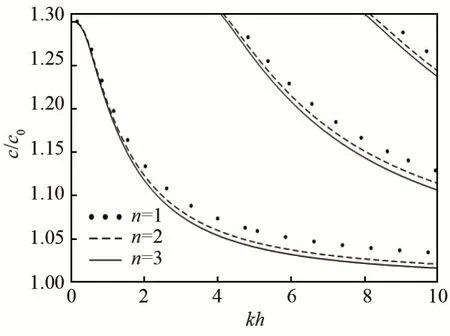
图3 不同n 值的Love 波频散曲线Fig.3 Dispersion curves of Love waves for different values of n
为了分析改进的拉盖尔多项式方法和传统拉盖尔多项式方法的区别,当覆层梯度指数n=1、k=2时, 分别使用两种多项式方法计算了PZT-2/PZT-4/BaTiO3半空间中Love 波第一阶模态的相对应力和相对电位移分布,如图4、5 所示。图4、5 中曲线进行了正则化(Tyz0和Dy0分别表示应力Tyz和电位移 Dy在x=0 处的值)处理。结果显示,使用传统拉盖尔多项式方法求得的正应力Txz和正电位移Dx在覆层和基体的交界(x=h=1 mm)处是不连续的,而且它们在覆层表面(x=0)处不为0,这与所假设的应力边界条件不符合。而改进的拉盖尔多项式方法能够很好地克服传统拉盖尔多项式方法的这些不足。
为分析高频处带有梯度压电覆层的压电半空间结构中Love 波的应力和电位移分布,计算了一种覆层梯度指数n=1 时,结构中Love 波的应力和电位移分布。覆层上表面x=0 处的材料为PZT-2,覆层下表面x=h 处的材料为PZT-4,压电半空间的材料为BaTiO3,简写为PZT-2/PZT-4/BaTiO3。图6 为在大波数k=20 时,梯度覆层半空间结构的相对应力和相对电位移分布。由于材料中的波速PZT-2<PZT-4<BaTiO3,如图6 所示,对于带有梯度压电层的压电半空间结构,高频Love 波的应力和电位移主要分布在功能梯度压电层中材料波速低的一侧。因此,可通过调节频率和覆层半空间材料组成,控制波的应力和电位移分布。
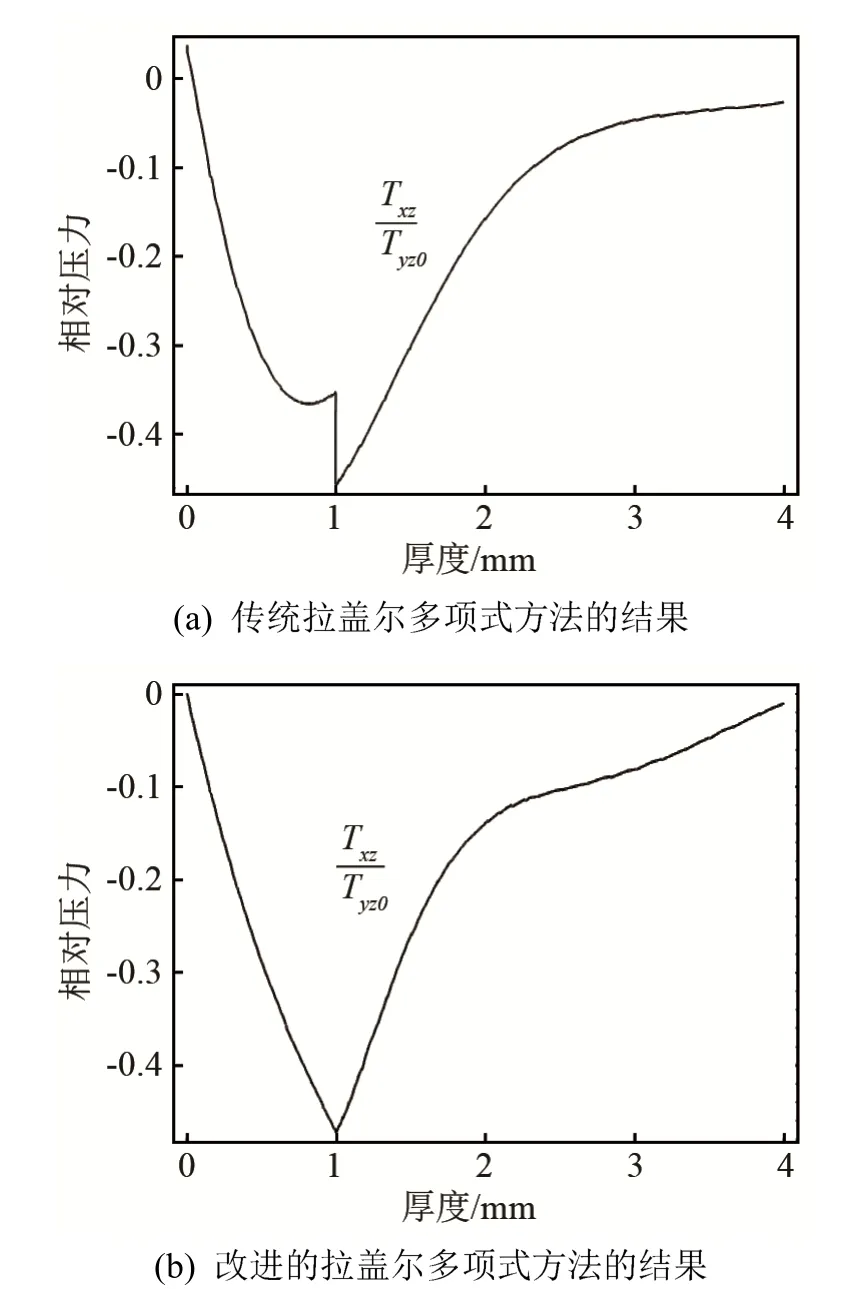
图4 k=2 时,Love 波第一阶模态的相对应力分布Fig.4 Relative stress profiles of the first order mode of Love waves at k=2
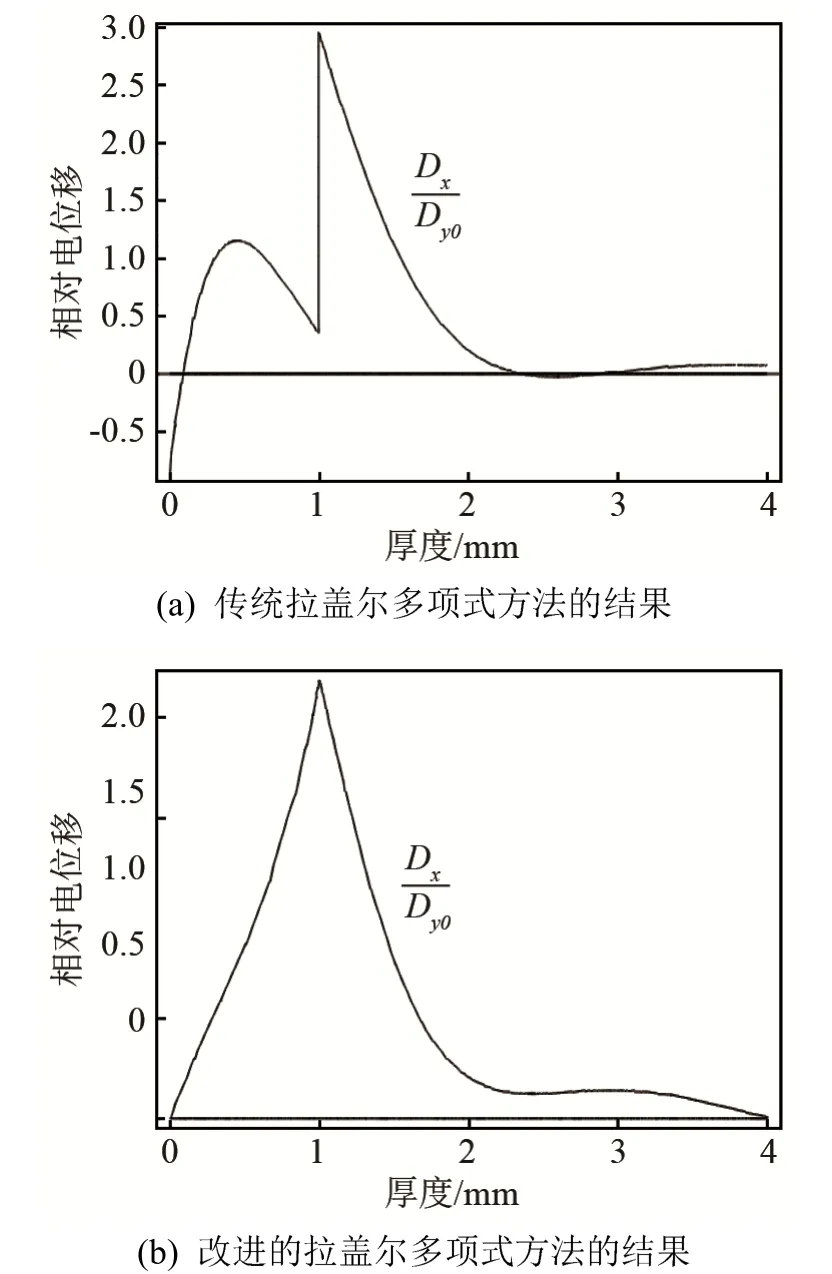
图5 k=2 时,Love 波第一阶模态的相对电位移分布Fig.5 Relative electric displacement profiles of the first order mode of Love waves at k=2
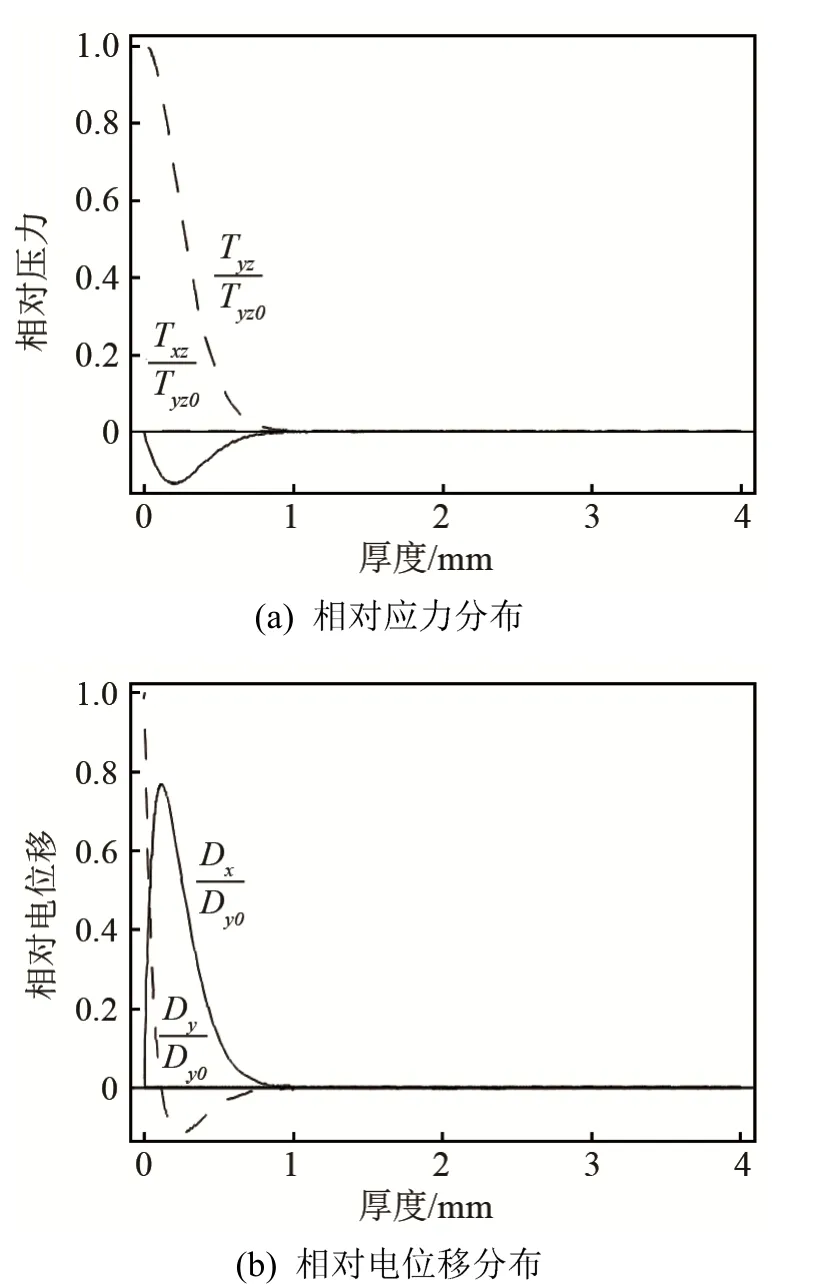
图6 k=20 时,PZT-2/ PZT-4/ BaTiO3 半空间中Love 波第一阶模态的相对应力和相对电位移分布Fig.6 Relative stress and relative electric displacement profiles of the first order mode of Love waves in PZT-2/PZT-4/BaTiO3 half-space at k=20
3 结 论
由于传统拉盖尔多项式方法在求解层状半空间结构的波传播问题时存在局限性,本文提出一种改进的拉盖尔多项式方法用于研究在功能梯度压电层状半空间结构中的表面波传播。由以上分析可以得到以下几点结论:
(1) 与已有文献结果比较,证明了改进的拉盖尔多项式方法的正确性。该方法能克服传统的拉盖尔多项式方法因层间材料差异所造成的波应力、电位移不连续的现象。
(2) 对于带有梯度压电覆层的压电半空间结构,Love 波频散曲线随着梯度指数n 的增加,相速度减小,频散现象更明显。
(3) 对于带有梯度压电覆层的压电半空间结构,高频Love 波的应力和电位移主要分布在功能梯度压电层中材料波速较小的一侧。
(4) 改进的拉盖尔多项式方法还可以推广应用于研究多覆层的压电半空间、磁电半空间等结构上的表面波传播特性。
