Floquet-Bloch 理论在频散曲线计算中的应用
2020-03-23童韫哲
童韫哲,范 军,王 斌
(上海交通大学高新船舶与深海开发装备协同创新中心海洋工程国家重点实验室,上海200240)
0 引 言
频散曲线在无损检测、弹性目标声散射机理及水声传播领域都有着广泛用途[1-5]。在水下目标声散射的研究当中,大量的实验结果表明,水下目标的回波中除了容易解释的几何散射波以外,总是会出现一些不易解释的非镜面散射波,这些散射波实际上是在弹性体中传播的波再辐射产生的[6]。所以计算弹性波的频散曲线,了解弹性波的传播规律,对水下目标声散射的精细特征研究具有至关重要的作用。
对于频散曲线的计算一般都归结为特征方程零点的求解:

其中:k 为行波波数;ω 为角频率。目前求解公式(1)的方法主要有三种:(1) 谱方法。该方法是一种较传统的解析方法。谱方法数值插值的方法直接求解特征方程,具有计算量小,计算精度高的优点[7-11]。(2) 半解析半有限元(Semi-Analytical Finite Element,SAFE)法。该方法结合了有限元与解析解表达式的特点,只对波导截面进行建模,因此降低了计算模型的维度[12]。(3) 波有限元(Wave Finite Element,WFE)方法。该方法利用波导的周期性,通过建立一部分波导的有限元模型以及周期边界条件获得相应的刚度矩阵,并求解特征根[13]。
鉴于目前的商用有限元软件的求解器能够非常成熟地应用周期边界条件求解特征方程,本文引入了波有限元(WFE)方法求解频散曲线[13]。常规有限元方法无法实现无限长的波导建模,所以需要引入基于Floquet-Bloch 理论的周期性边界条件。Floquet 理论是微分方程理论的一个分支,它是求解形如x (t ) = A (t )x (t )的周期性线性微分方程的一种方法,其中A (t )是周期为T 的分段连续周期函数,在固体物理学中叫做Bloch 理论。
1 Floquet-Bloch 理论在求解弹性体频散曲线中的应用
有限元方法求解弹性体频散曲线的关键在于利用Floquet-Bloch 理论将长度为L、高度为h 的有限长弹性体控制方程中的位移/振速写成行波形式。省略时间因子eiωt,弹性体控制方程可以写成:

其中:σ 是应力张量,u 是位移张量。将位移u 的解写成平面波的形式:

公式(3)表示某一特定振动状态f (y )沿着x 方向以行波的形式传播,振动状态只是y 的函数,在传播过程中不发生变化,长度为L、高度为h 的计算单元示意图如图1 所示。
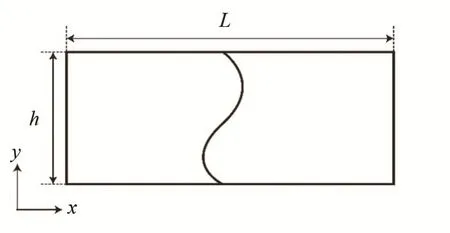
图1 计算单元示意图Fig.1 Schematic diagram of calculation cell
长度为L 的单元左边位移和右边位移存在如下关系:
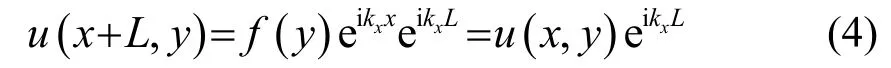
由于u 以行波方式沿着x 方向传播,振动状态与x 无关。二维无限长板可以近似认为沿x 方向周期为L 的周期性结构,利用Floquet-Bloch 理论,存在如下关系:

其中:kFB是Floquet-Bloch 理论的指数因子,kFB与x 方向的波数kx有如下关系:

详细理论推导参见文献[13]。
2 有限元计算结果与谱方法的对比
有限元在求解频散曲线时的困难在于无法建立无限长的波导,Floquet-Bloch 理论实际上是对如图1 所示的计算单元施加边界条件以模拟无限长波导。COMSOL 软件中Floquet 周期边界条件模块能够实现这一功能,其公式为
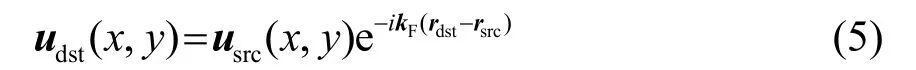
其中:usrc和rsrc是源边界的位移和坐标;udst和rdst是目标边界的位移和坐标,详细信息参见文献[14]。
在COMSOL 软件中建立如图2 所示的模型,在模型两边添加Floquet 周期性边界条件,并输入不同的行波波数kF,将有限长区域模拟成无线长波导,再利用特征频率求解器求解相应kF所对应的特征频率ω。
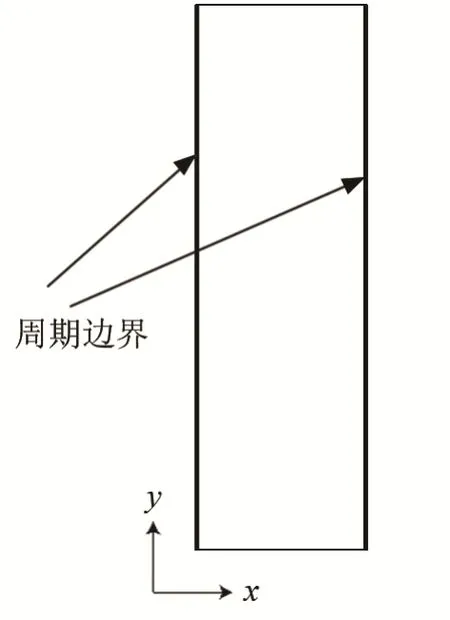
图2 有限元计算示意图Fig.2 Schematic diagram of finite element calculation
因为只考虑沿x轴传播的行波,所以向量kF在y 轴投影为0,令其在x 轴的投影为kx。由式(6)可知,当n=1时,kx的取值范围是0~2π /L,实际上kx取0~π /L最合理,具体情况会在下文讨论。使用COMSOL 的搜根求解器可以求得kx满足计算单元的特征方程所对应的所有特征频率f,由特定的kx及与其对 应的特 征 频 率f 可求得 对应 的 相速度Cp= 2π f/ kx。本文计算了两边真空的弹性平板频散曲 线,参数为:ρ=7900 kg·m-3,纵波声速CL=5940m·s-1,剪切波速CT=3 100 m·s-1,板的厚度h=40mm。

图3 有限元与谱方法计算结果对比图Fig.3 Comparison of calculation results of WFE method and spectral method
图3 为有限元与谱方法[3]计算结果对比,横坐标为频率与板厚之积,纵坐标是相速度Cp与剪切波速之比。两者吻合得非常好,从而证明了基于Floquet-Bloch 理论的有限元建模方法的正确性。
3 对于计算单元长度与高度之比值R的讨论
选取合适的R(R 为计算单元的长度L 与高度h之比)对于计算结果至关重要。本文所提到的方法是用Floquet-Bloch 周期边界条件模拟无限长的情况,所以存在一定的局限性,这一局限性主要体现在R 的大小与计算结果的关系。
图4 是相同计算参数、不同R 值的计算结果,红线分割了计算结果的有效区和无效区。由式(4)中 eikxL的周期性和对称性可知波数kx必须满足:

因此,kx所对应的特征频率f 和相速度Cp必然满足:

对公式(7)乘以厚度h,经过变换可以得到相速度pC 与频率必须满足:
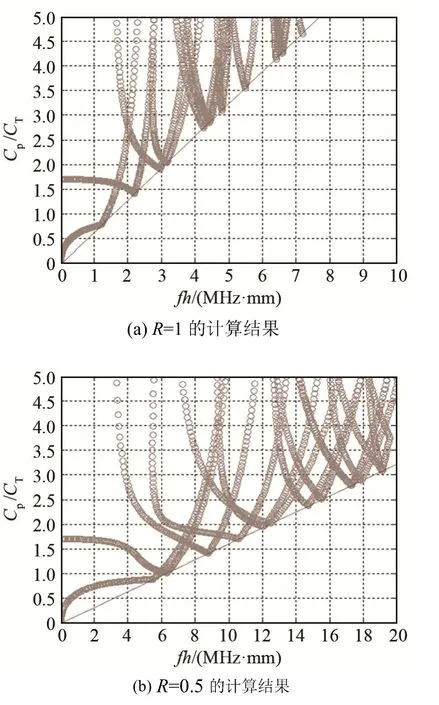
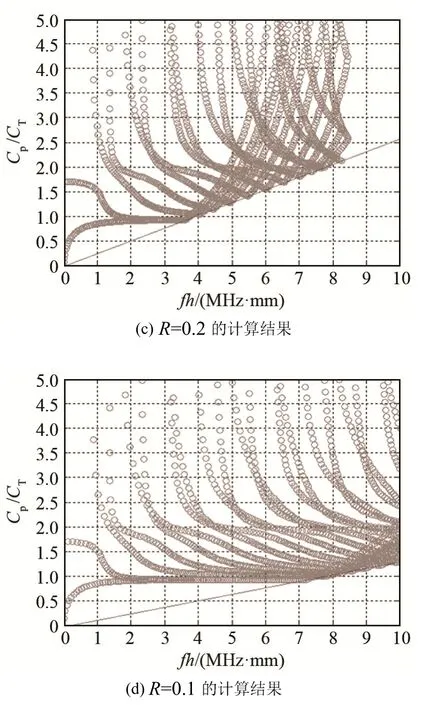
图4 不同R 计算结果对比Fig.4 Comparison of calculation results of WFE method for different R values

由图4(a)~4(d)可以看出:计算结果的有效区域随R 的减小而增大,这一规律完全符合公式(13)。此外,根据经验可知,当R=0.1 时计算结果较好,本文中的图3 即是使用R=0.1 计算得到的结果。
4 结 论
本文简要阐述了Floquet-Bloch 理论及其在频散曲线计算上的应用。在此基础之上,分析了其计算结果的局限性,为将此方法进一步应用于更加复杂的计算奠定了基础。
本文得到以下主要结论:
(1) 利用基于Floquet-Bloch 理论的周期性边界条件的有限元建模方法,能够准确计算弹性体的频散曲线;
(2) 通过周期性边界条件将有限长弹性体近似成无限长波导存在一定的局限性,这一局限性体现在计算单元长度与高度之比R 对于计算结果正确区域的影响;
(3) 使用有限元法计算频散曲线较之传统的迭代法与谱方法有着操作简单、不受波导形状影响等优势。
