改进的相控阵多普勒计程仪波束形成技术

王述思，刘 宇，许伟杰

(1. 中国科学院声学研究所东海研究站，上海201815；2. 中国科学院大学，北京100049)

0 引 言

多普勒计程仪(Doppler Log, DVL)可以对水层及水底测速，其优点是准确性好、灵敏度高、受环境影响不大，被广泛应用于船舶上，为其提供船舶纵向和横向运动的精准数据。多普勒计程仪的原理是利用声学换能器所发射的声脉冲和接收的水底或海中颗粒物反射声脉冲之间的多普勒频移而进行流速测量和航程累计[1]。声学多普勒流速剖面仪(Acoustic Doppler Current Profiler，ADCP)[2]是20 世纪80 年代初发展的一种测流设备，目前被广泛应用的相控阵式ADCP设备的基阵体积比传统活塞式ADCP 的基阵体积已经缩减了很多，但在中深度及大深度测量所采用的ADCP 设备中，换能器基阵的体积仍限制了为其适装的ADCP 的种类。在相同频段、相同作用深度的条件下，国外已经研发出尺寸较小的相控阵产品，而国内还没有研发出类似产品。国内在多普勒计程仪小型化方面与国外存在着巨大的差距，主要表现在：(1) 电子部件集成化程度低。国外电子器件的发展水平远远超过国内，核心信号处理模块性能的大幅提升，尤其运算能力的提高，使得原本需要硬件实现的功能可以通过软件算法来实现，从而可以大大缩小硬件模块的体积，再加上电子部件本身的高度集成化设计，使设备的电子部件可以做到体积非常紧凑。(2) 水下换能器基阵体积庞大，虽然目前相控阵式多普勒计程仪的基阵体积比活塞式多普勒计程仪已经缩减了很多，但在中深度和大深度多普勒计程仪设备中，换能器基阵的体积仍然限制了其适装载体的种类。(3) 没有形成系列化产品，国外的多普勒计程仪产品基本涵盖各个频段，早已经形成系列化产品，并且根据不同的使用环境和用途还可以细分成几个子系列的产品，而国内产品大都品种单一，只针对某种需求而设计，难以形成系列化产品。

针对上述问题，本文分析一种密排相控阵模型，通过仿真对比不同指标，分析出密排相控阵模型比稀疏相控阵模型在指向性处基本无差别，但在声源级与信噪比上均可提高3 dB。

1 稀疏相控阵波束形成

本节以频率为75 kHz 的稀疏相控阵ADCP 为例，研究它的波束形成原理。假设在均匀海水中，声波在水中的速度可看做定值，设为1 500 m·s-1，频率为75 kHz 的声波波长为20 mm，阵子间的距离则为10 mm，图1 为传统相控阵阵元排列模型。由图1 可知，整个阵列排布了988 个阵子，设计为圆形阵，直径为370 mm，共有36 行36 列。将988个阵元分成黑色与白色两个部分，从图1 中可以看到黑色阵元与白色阵元为对称关系，黑色阵元可产生左右两束声波，白色阵元则产生上下两束声波，共同组成詹呐斯(Janus)配置的4 个波束[3]。

由于黑色阵子与白色阵子具备相同性质，为简便计算过程，只分析黑色阵子。黑色阵子从左至右的列序号为1～36，共有36 列，若将左侧第一行列序标定为1，则第一列黑色阵元包含3 个阵元，第2 列黑色阵元包含6 个阵元……每列最少阵元数为3 个，最多阵元数为18 个。

图1 稀疏相控阵阵元排列模型Fig.1 Sparse phased-array elements arrangement model

设第一列阵元接收到的信号为[4]

则第i 列阵元接收到的信号为

式中：iA 为子阵列的接收灵敏度，随子阵包含阵元数目的不同而不同；ω 为信号角频率；φi是第i 列与第一列的相位差值，即：

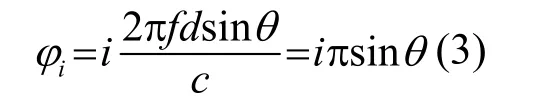
式中，θ为波束角。

相控阵的总输出可以表示为

1.1 发射波束的相移波束形成

对于阵元数为N 的发射相控阵，可将各个阵元的极性按照正-负-负-正排列，即相邻两个阵元当做一个偶级子，将这N /2个偶级子线性排列，计算N /2个偶级子的指向性函数即可得到发射波束的两个波束。先计算得到相邻阵元间的距离为

各个阵元的极性按照正-负-负-正的规律排列后，两两组合，即一奇一偶当做一个偶级子，并将一奇一偶的中心点当作这一偶级子的中心，依次类推，将出现N /2个偶级子，每个偶级子间的距离为2d，且每个相邻偶级子极性不同。最终，N 个阵元的线性排布转化为N /2个偶级子且每个偶级子距离为2d 的线性排布。由乘积定理可知，该阵元的指向性由两个函数的乘积决定，一是单个阵元的指向性函数，二是N 个阵元组成的线性阵的指向性函数[4]。

1.2 发射指向性阵元的指向性函数

根据相控阵各个阵元的互易性可以证明，发射指向性阵元的指向性函数与接收指向性阵元的指向性相同。

设1 号正阵元的输出电压为

则2 号“负”阵元的输出电压为

这两个阵元经过加法器输出的电压为

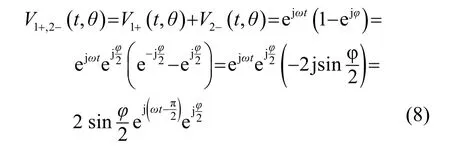
因此，该指向性阵元的指向性函数为

则指向性阵元的指向性函数可化为

1.3 线阵阵元的指向性函数

下面计算N/2 个偶级子排列的线阵阵元的指向性函数。由于N/2 个偶级子按照正-负-正-负的顺序排列，每两个阵元间的的相位差相同，为φ+ π，所以可得由N/2 个点阵元组成的指向性线阵的指向性函数为

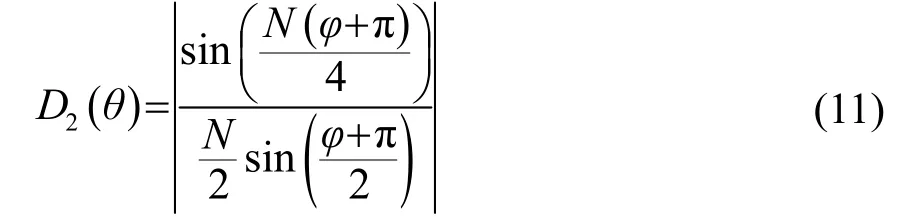
由于N 为4 的整数倍，可得：

其中阵元间距为2d，则可得：

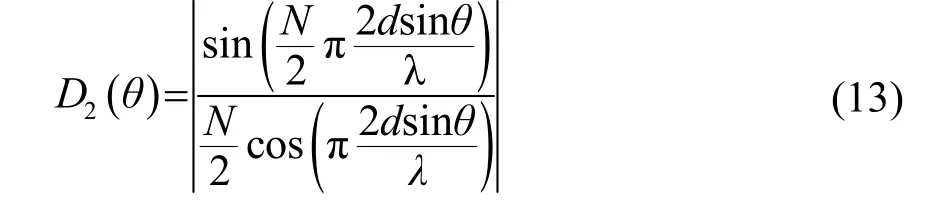
1.4 指向性阵元组成线阵的指向性函数

根据乘积定理可得整个阵列的指向性函数，进行归一化后得：

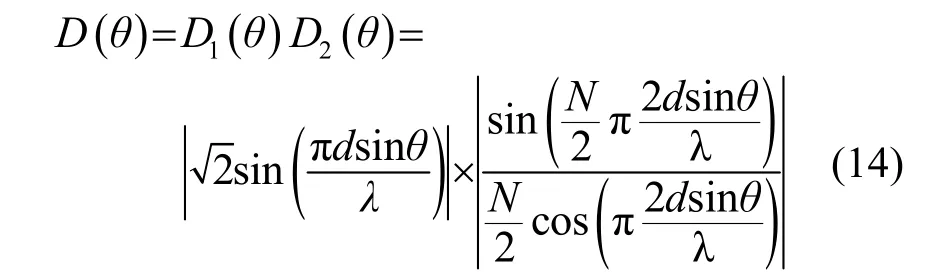
根据式(14)，进行MATLAB 仿真，针对黑色阵元的36 列子阵，将其按照正-负-负-正排列，将所有子阵的输出加起来，即可得到发射波束的指向图，D( θ )在 θ=±30°处各有一个主瓣。

2 密排相控阵波束形成

稀疏相控阵形成前后或左右波束时，发射和接收都只有一半的阵元参与，本节所研究的密排相控阵形成前后或左右波束时，其所有发射和接收阵元都参与波束形成。图2 为密排相控阵阵元排列模型。

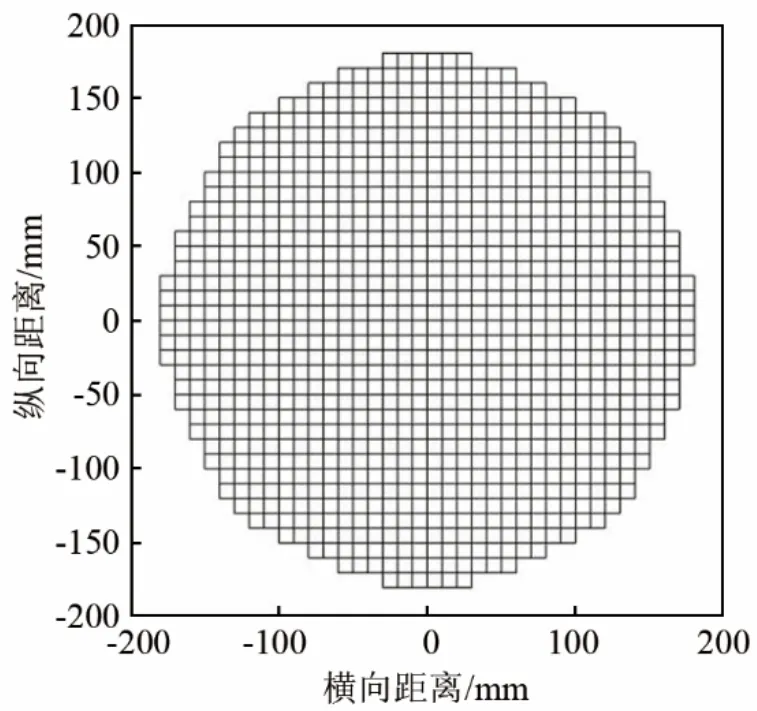
图2 密排相控阵阵元排列模型Fig.2 Dense phased-array elements arrangement model

密排相控阵的指向性与稀疏相控阵指向性推导过程类似，不同的是，密排相控阵每个阵元对垂直阵列形成的水平波束以及水平阵列形成的垂直波束都起到了作用。图3 为密排相控阵的连线方式。

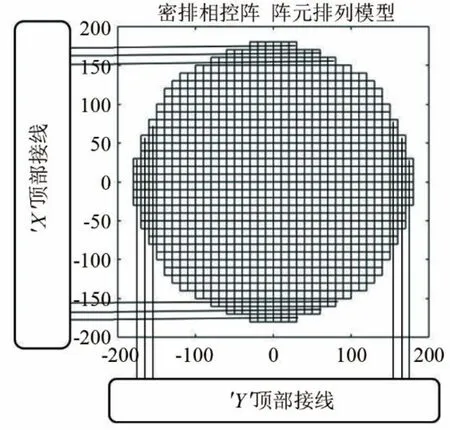
图3 密排相控阵阵元连接方式Fig.3 The wiring mode of densely arranged phased-array elements

序号为1,5,9…33的行并联在一起，记为V1。序号为2,6,10…34 的行并联在一起，记为V2。序号为3,7,11…35的行并联在一起，记为V3。序号为4,8,12…36 的行并联在一起，记为V4。序号为1,5,9…33 的列并联在一起，记为H1。序号为2,6,10…34的列并联在一起，记为H2。序号为3,7,11…35 的列并联在一起，记为H3。序号为4,8,12…36 的列并联在一起，记为H4。当频率为工作频率的声波，从阵的正上方且与阵的法线夹角为30°的方向入射时：若V1上的电信号的相位定义为0°，则V2上的电信号的相位应为90°，V3上的电信号的相位应为180°，V4上的电信号的相位应为270°。当频率为工作频率的声波，从阵的正左方且与阵的法线夹角为30°的方向入射时：若H1上的电信号的相位定义为0°，则H2上的电信号的相位应为90°，H3上的电信号的相位应为180°，H4上的电信号的相位应为270°。将V1上的信号SV1与V3上的信号 SV3作运算得SV1,3，将V2上的信号 SV2与V4上的信号SV4作运算得SV2,4，对SV2,4进行适当移相后与SV1,3相加就可以形成艏波束或艉波束的输出。将H1上的信号 SH1与H3上的信号 SH3作运算得SH1,3，将H2上的信号SH2与SH4上的信号SH4作运算得SH2,4，对SH2,4进行适当移相后与SH1,3相加就可以形成左波束或右波束的输出。稀疏相控阵多普勒计程仪为了实现同时发射4 个波束，将阵元一分为二，并利用偶极子可同时形成两个波束的特性。通过适当的电路设计，可以实现密排相控阵同时发射4 个波束，提高发射声源级。

3 仿真分析对比

本节通过对密排相控阵和稀疏相控阵的仿真结果，对发射指向性、发射声源级、信噪比、阵元连接方式进行比较。

3.1 发射指向性

相控阵多普勒计程仪发射信号的中心频率为75 kHz，对于发射相控阵而言，需要同时产生两个方向分别为+30°和−30°的波束。图4、图5 分别是密排相控阵和稀疏相控阵的发射指向性图，从图像中可以看出，主瓣宽度基本一致，即定位精度一致，密排相控阵在±50°和±70°附近，旁瓣明显降低。图6、图7 分别为密排相控阵和稀疏相控阵的发射波束空间指向性图，从图中可以看出，密排相控阵旁瓣幅值明显降低，可以抑制旁瓣干扰。

图4 密排相控阵发射波束指向性图Fig.4 Beam directivity pattern of element densely arranged phased-array

图6 密排相控阵发射波束三维空间指向性图Fig.6 Three-dimensional transmitting directivity pattern of element densely arranged phased-array

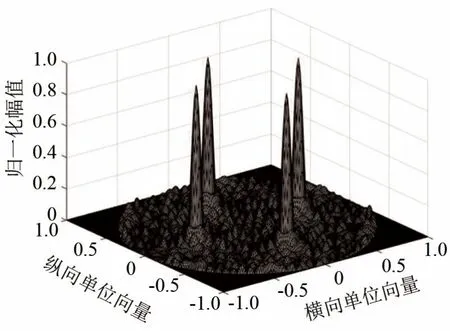
图7 稀疏相控阵发射波束三维空间指向性图Fig.7 Three-dimensional transmitting directivity pattern of element sparsely arranged phased-array

3.2 发射声源级

发射声源级是指声轴上距离声源1 m 处产生的声强相对于参考声强的分贝数，是声呐方程中定量描述声源辐射能力的参数，用LS表示。设阵元总发射电功率为Pe，每个波束功率为50 W，则4 个波束的发射电功率为Pe=200 W，阵元数为988，单阵元发射声源级LSe可以表示为[5]

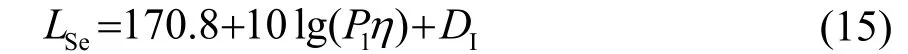
其中，P1为单个阵元的发射电功率，η= 0.5为电声转换效率， DI= 4.056 3为指向性因数。

其中，N 为等效阵元个数。

稀疏相控阵中参与发射前后或左右两波束的有效阵元个数为494 个，， LSe=170.8 +10lg ( 0 .2402× 0 .5) + 4.0563 ≈1 65.7 dB ，等效阵元个数为N= 494× 1 = 494，计算可得4 个波束的发射声源级为219.57 dB；全阵相控阵中有效阵元个数为988 个，，同理 LSe≈1 65.7 dB，可得等效阵元个数为N=988× 0 .707 ≈698，计算可得4 个波束的发射声源级为222.57 dB。综上所述，密排相控阵比稀疏相控阵发射声源级增加约3 dB。由于密排相控阵接收的阵元数增加了一倍，使得接收阵增益增加了3 dB，因此接收信噪比也增加了3 dB，可进一步提高作用距离。

3.3 阵元连接方式

本文中的ADCP，其中心频率为75 kHz，由988个阵元组成平面相控阵，阵元排列如图1 所示。黑白阵元共组成72 路子阵，采用相移波束形成[6]。72路子阵根据规律并成8 路子阵，其中4 路子阵形成左右两个波束，另外4 个子阵形成上下两个波束，最终构成经典的Janus 配置模型。根据以上需求，在硬件方面需要对8 路相移通道进行控制，共需72根水平连接线，72 根垂直连接线，不可避免地存在连线的重叠。而在密排相控阵波束形成中，72 路子阵根据规律形成2 路子阵，每一个子阵各形成左右、上下两个波束，总需36 根水平连接线，36 根垂直连接线，可以避免连线的重叠。阵元间的接线方式如图3 所示。

4 结 论

本文在详细分析多普勒计程仪相控阵波束形成的基础上，分析了密排相控阵波束形成方法。针对密排波束形成技术，比较其发射指向性、发射声源级、信噪比、系统复杂度与稀疏相控阵的差异。分析表明，在相同频率、相同发射功率以及相同尺寸条件下，密排相控阵的收发联合响应较稀疏相控阵提高近6 dB，说明在同等条件下，密排阵相控阵DVL 的作用距离会更远。反之，如果要求相同的测速作用距离时，采用密排阵相控阵方式就可以减少换能器的阵元数，从而减少换能器尺寸来达到与稀疏阵DVL 采用较大换能器尺寸时同样的作用距离。